防雷接地参数对雷电波传输过程的影响

秦培林, 吕泽红

(1.广西机电职业技术学院 电气工程系,南宁 530007;2.广西博阳电力勘察设计有限公司，南宁 530072)

0 引 言

Portela[1]提出了解决随频率变化的接地电阻率和介电常数对输电和配电线路的雷电过电压的影响的办法。研究人员往往使用针对性较强的算法进行计算分析，当面对更复杂的电力系统网络,例如：分析带分支线的输电线、多点接地、避雷器保护、绝缘击穿和设备待检修等情况时，使用这些计算方法便出现了较大困难[2]，为了解决该问题，研究人员开发了一种可以对包含分散式接地参数的复杂电力系统进行分析计算的程序，即电磁暂态分析程序(ATP)。该软件可以提供电力系统组件的基准模型，并且适应于用户自定义模型[3]。

Portela等[4]基于ATP计算平台对JMarti模型进行了修改，例如在输电线路参数的计算中，将随频率变化的接地参数纳入考虑和计算范围内。本文将该修改过的JMarti模型直接应用于研究分散性接地参数对一个单相配电变压器的低压侧相电压的影响。

1 模型搭建

本文的研究模型是某城郊的一条输配电线路，如图1所示。在该配电线路的计算模型中，使用两条垂直堆叠的导线分别代表相导线和中性线。两条导线架设的高度分别为8.4 m和7.2 m，假定导线半径为0.85 cm。该线路匹配在整个模型的左端，延伸长度为1.5 km，终端接入一个单相配电变压器的高压侧。该变压器的高压端使用氧化锌避雷器进行保护，其中压端为开路。中压线路的中性线(零线)以每150 m的间隔设置一次接地，变压器极也一同接地。相导线安装在针式瓷绝缘子上，绝缘子临界闪络电压(CFO)为100 kV。

图1 终端接入配电变压器高压端的城郊配电线路

假设雷电直击距离变压器600～1 200 m范围内的中压输电线上。本文仿真试验是根据具有不同假设条件的模型，计算其变压器低压侧相电压的值。

2 建模参数

2.1 输电线路模型

图1的双相配电线路采用了马蒂输电线模型,马蒂模型是使用模态理论求解输电线路的时域方程。在这种情况下，一个系统的n条耦合导线通过等效变换表示为n条独立的单相线。马蒂模型使用连续实数矩阵变换的方法计算时域电压和电流[5]。

马蒂模型是能为ATP兼容的一个输电线路模型[6]。与此同时，在马蒂模型中输电线路的参数计算中，采用了卡森方法来计算接地阻抗参数，卡森方法将频率设定为近似低频并假定1/ρ>>ωε，其中:ρ是电阻率;ω是角频率;ε是土壤的介电常数。上述约束条件表明,卡森方程在处理雷电过电压的相关研究计算时只有在土壤属于相对良导体的情况下才能够适用。此外，卡森方程中只有接地电阻率参数可以进行效果较好人为的修正。除此以外，在ATP中应用卡森方程计算输电线路参数时，只能使用恒定的接地电阻率(即接地电阻率与频率无关)。综上所述，当土壤为非良导体时，利用ATP计算雷电过电压的电磁暂态过程会非常困难。

为了解决上述问题，本文利用Matlab对考虑了分散式接地参数的输电线路参数进行计算，然后将带有极点和留数的传输函数以及特性阻抗参数拟合成为一个有理函数，在ATP软件中以.pch文件的格式进行读取，并且在马蒂模型中调用。在本文的分析计算中，采用那卡嘎瓦方程[7]计算输电线路参数，由于土壤性质存在缺陷，并且此处的计算中将土壤假设为单一层，故可以忽略导纳的修正问题。使用上述方法计算得出的结果与Sunde方程得到结果几乎相同。当土壤的相对介电常数假设为1时，卡嘎瓦方程可以归纳为卡森方程中的一种情况[8]。

2.2 接地参数模型

本文将下列两个方程[9]用于接地阻抗的计算：

(1)

(2)

式中：ρr(ω)定义为ρ(ω)/ρ0，它是一个实数电阻率，ρ(ω)为土壤电阻率，ρ0是当频率为100 Hz时的接地电阻率;εr(ω)为实数的土壤介电常数，其中频率f是可变的。方程(1)和(2)有效的频率范围为0.1～4 MHz,随着频率的增加接地电阻率和介电常数也会同步增加，该结果与实验观测相一致。

2.3 变压器模型

本文考虑将一台容量和电压为10 kVA 7.967 kV/240～120 V的单相电力变压器用于该模型线路中。这个变压器有4个可用的电压终端，一个高压端，两个对称且带有中心抽头的低压端，还有一个接地的中压端。本文对频率范围为0.01～3 MHz的二端口模型进行了仿真计算。计算模型由初始3×3变压器导纳矩阵，减去假设一个低压端终端开路时得到的2×2矩阵导出，将所得到的结果利用导纳矩阵元素配合矢量技术进行拟合。使用上述变压器模型计算得到的变压器相电压值结果与采用1.2/50 μs的标准雷电波进行变压器高压端试验后得到的实验数据吻合度较好。

2.4 绝缘子、引下线和接地模型

本文采用了文献[10]中所列举的破坏性模拟试验的试验参数，以及前文中所述模型的ATP子程序，对绝缘击穿的情况进行建模仿真计算。本文假设一根半径为0.5 cm，长为7.2 m的垂直导线来对引下线以及其连接的中性点接地电极进行建模，根据约旦方程[11]，垂直导线的电感为11 μH。为了简单起见，将所有接地点替换为阻值为100 Ω的电阻器。

2.5 雷电流模型

本文的仿真计算均使用ATP软件中的单一Heidler函数来表示幅值为10 kA雷电流。雷电流波形参数为波前时间0.5 μs，半峰值时间25 μs。根据文献[12]中的结论在仿真计算中用等效诺顿电路表示任何形式的雷电流通道，雷电流诺顿模型由一个理想电流源以及一个并联电阻构成，其中并联电阻值为1.5 kΩ，以此表示雷电流通道的阻抗[13]。

3 结果分析

3.1 接地电阻率的影响

一般接地参数的分散性在高电阻率的土壤中表现较为显著。本文通过考虑马蒂输电线路模型中计算接地阻抗时的两种不同的可能性，分析接地电阻率对变压器低压侧相电压的影响，其中一个使用了恒定电阻率下的卡森方程;另一个考虑了接地电阻率和介电常数的频变特性。为了简化计算，首先忽略变压器高压端的绝缘击穿现象和避雷器的保护作用，并且假设变压器的中压侧开路，计算低频下接地电阻率为1～10 MΩ时变压器低压侧相电压的值。图2所示为距离变压器600 m远处发生雷电直击时的计算结果。图3所示为距离变压器1 200 m远处发生雷电直击时的计算结果。

(a) 1 MΩ·m

(b) 10 MΩ·m

图2 雷电直击距离变压器600 m远处时，电压转移到变压器低压侧的情况

由图2可知，计算所得到的结果与用于计算接地电阻率的值的方程无关，因此，需要考虑随频率变化的分散性土壤接地参数。如图3所示，距离变压器1 200 m处遭遇直击雷，这种情况下输电线中的波过程的影响更为重要，与此同时当接地电阻率达到10 MΩ时两种接地参数之间的差别更加显著，但仍旧可以忽略。

3.2 变压器高压端绝缘击穿的影响

考虑中压线路接入变压器的位置处所发生的绝缘击穿现象。为了简化计算以及方便比较，变压器的高压侧仍然假设为未使用避雷器进行保护，其仿真结果如图4和图5所示，这两种情况分别为在距离变压器600 m和1 200 m远处遭遇直击雷。同样，此处接地阻抗参数的计算分别使用了恒定接地电阻率条件下的卡森方程[14]，以及接地电阻率随频率变化条件下的卡嘎瓦方程，其中ρ0分别为1 MΩ和10 MΩ。

(a) 1 MΩ

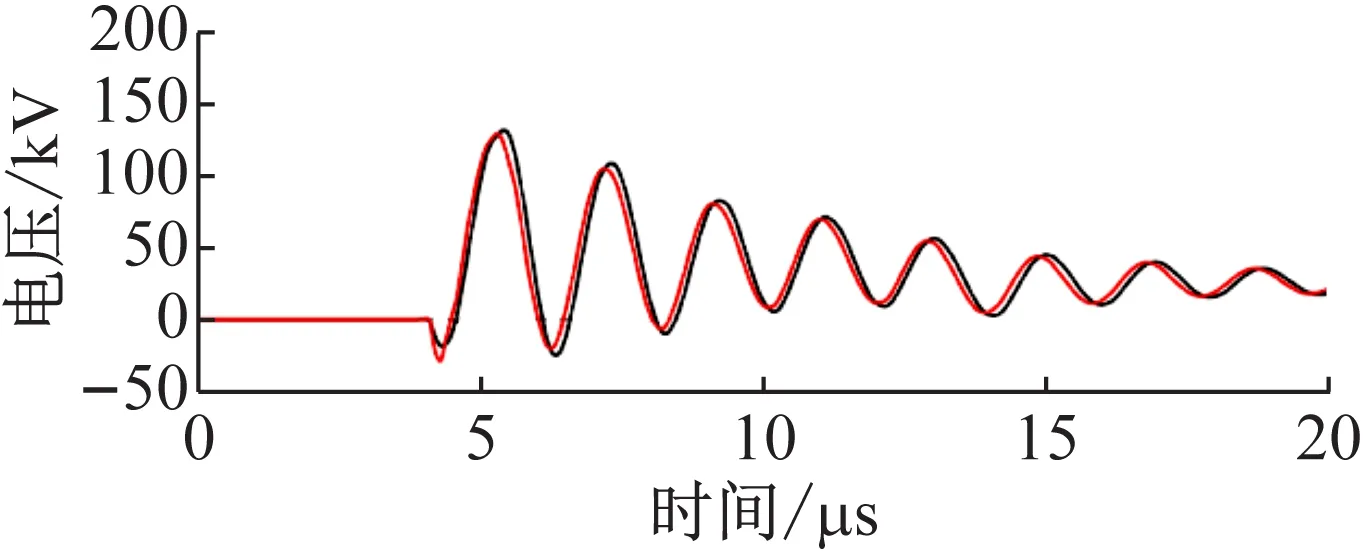
(b) 10 MΩ

(a) 1 MΩ·m

(b) 10 MΩ·s

图4 距离变压器600 m处遭遇直击雷，考虑绝缘击穿时的变压器低压侧相电压的幅值

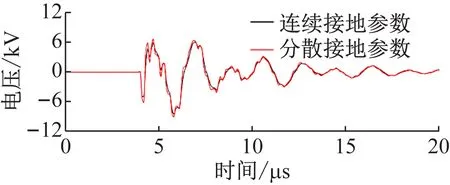
(a) 1 MΩ·m

(b) 10 MΩ·m

如图4和5所示，当中压线路与变压器高压侧联结处的绝缘发生击穿时，变压器低压侧的相电压明显下降。对比图2和图3的结果，绝缘击穿时计算得出的相电压值相比绝缘未击穿低了83%。

关于分散性接地参数对变压器低压侧相电压影响的情况[15]，与忽略绝缘击穿的情况下得出的结果基本相同。当接地电阻率为1 MΩ·m时，本文利用卡森方程计算接地回路阻抗得到的结果，与接地参数随频率变化时利用卡嘎瓦方程计算得到的结果几乎相同。当接地电阻率为10 MΩ时仿真计算得到的差异更加显著，特别是当雷电直击在距离变压器1.2 km处的位置上时。通过仿真可以知道，无论是否考虑接地参数的分散性，所得到的计算结果都具有很高相似性。

3.3 避雷器保护变压器高压侧时的影响

在变压器的高压侧加入一个避雷器。图6和图7分别表示雷电直击距离变压器600 m和1.2 km处时的结果。由图可以看出,在变压器高压侧加上避雷器后低压侧相电压的幅值可以减小到2 kV以内。当雷电直击距离变压器1.2 km处时，仿真结果的差异更为明显，并且接地电阻率为10 MΩ·m时，可以通过图中波形观测到是否考虑接地参数分散性时，转移电压波形的差异。

(a) 1 MΩ·m

(b) 10 MΩ·m

图6 距离变压器600米处遭遇直击雷，考虑中压线路的绝缘击穿以及在变压器的高压侧添加避雷器保护时的结果

(a) 1 MΩ·m

(b) 10 MΩ·m

4 结 语

过电压的计算结果表明,仿真计算时中压线路的不同计算参数直接影响着过电压振荡特性以及振幅。计算得出当考虑中压线路上的变压器高压侧绝缘击穿以及变压器高压侧带避雷器保护时，变压器低压侧相电压的幅值不超过2 kV。在试验中，假定接地电阻率为常数以及忽略土壤介电常数得到结果中，计算变压器配电线路的接地阻抗(使用卡森方程)得到的值与假设接地电阻率和介电常数与频率有关时(使用卡嘎瓦方程)得到的值几乎相同。这表明，至少在本文考虑的理想情况下(同时忽略低压线路的存在以及用户的消耗)，分散性接地参数对变压器低压侧相电压的影响可能不大。

参考文献(References)：

[1] Portela C M. Measurement and modeling of soil electromagneticbehavior[C]//In Proc IEEE Int Sym Electromagnetic Compatibility.Seattle, WA, 1999: 1004-1009.

[2] 扈海泽,刘小丽,毛 弋,等. 特殊防雷接地系统技术研究[J]. 电瓷避雷器,2016,12(3):68-73.

[3] 柴 健,杨仲江,孙 京. 一种用于计算雷击接地网时最小冲击接地阻抗值的方法[J]. 电瓷避雷器,2012,12(3):77-81.

[4] Portela C, Tavares M C, Pissolato J. Accurate representation of soil behavior for transient studies[J]. IEEE Proceedings on Generation,Transmission and Distribution, 2003,150(6):734-744.

[5] 杨文斌,周 浩. 风电机组过电压保护与防雷接地设计[J]. 高电压技术,2008,10(3):2081-2085.

[6] 黄荫明. 云闪监测与防雷接地检测系统研究及应用软件设计[D].成都:电子科技大学,2013.

[7] Portela C, Gertrudes J B, Tavares M C,etal. Earth conductivity and permittivity data measurements-influence in transmission line transient performance[C]//In Proc IPST’2005-International Conference on Power Systems Transients. Montreal, Canada, Jun. 2005.

[8] Visacro S, Alipio R. Frequency dependence of soil parameters: experimental results, predicting formula and influence on the lightning response of grounding electrodes[J]. IEEE Trans Power Del, 2012,27(2): 927-935.

[9] 李德超,张玉环,李玉玲,等. 两种杆塔接地电阻率测量方法的比较[J]. 电瓷避雷器,2008,12(2):39-42+46.

[10] Alipio R, Visacro S. Modeling the frequency dependence ofelectrical parameters of soil[J]. IEEE Trans Electromagnetic Compatibility, 2014,56(5): 1163-1171.

[11] 邓慧都,周力行,何腾芳,等. 雷电流流经故障垂直接地体时暂态阻抗的时域分析[J]. 电瓷避雷器,2014,12(2):60-65.

[12] Zhu B, Sima W, Yuan T,etal. The influence of soil permittivity’s frequency dependent characteristics on impulse transientresistance of grounding electrode[C]//In Proceedings of GROUND’2014 International Conference on Grounding and Earthing. Manaus, Brazil, May, 2014.

[13] 贾东瑞,谢兴利,赵东成. 基于ATP的500 kV GIS变电站雷电侵入波过电压分析[J]. 电瓷避雷器,2013(6):100-105,111.

[14] 方书博,李 牧,张晓琴,等. 500 kV同塔双回线路过电压计算及杆塔操作冲击最小空气间隙选择[J]. 电瓷避雷器,2016(2):106-110.

[15] 卢文浩,陈 伟,黎卫国. ±800 kV糯扎渡直流输电工程人工接地短路试验中性母线避雷器故障原因分析[J]. 电瓷避雷器,2015(5):149-153.