多点同步起爆条件下环形射流成型及 侵彻过程的数值模拟

吴海军， 王可慧， 柯 明， 龚柏林， 李 明

(西北核技术研究所, 西安 710024； 强动载与效应重点实验室, 西安 710024)

环形射流是一种特殊结构的线性聚能装药形式，具有体积小、破甲能力强的特点，能够实现对靶板的大口径开孔，其独特的作用效果受到了国内外学者的关注。Chick将线性聚能装药弯折为环形，形成了环形射流，但实验中发现用此方法形成的射流成型效果不稳定[1]。王成对W型聚能装药进行了实验和数值仿真，证明W型装药结构形成的环形射流可在靶板上形成环形孔，但侵彻孔径和深度较小，平均侵彻孔径为0.5倍装药直径，侵彻深度0.625倍装药直径[2-3]。吴成针对环形聚能装药药形罩内外壁质量非对称的问题，根据等动量原则，提出了环形聚能装药药形罩的质量补偿设计方法[4]，但该方法在工程上难以实现。李永胜采用数值模拟方法对环形聚能装药进行了优化设计，指出60°锥角、柱锥状装药的环形聚能装药对靶板的切割效果最理想，简单比较了环向2点、4点、8点以及环向线起爆条件下环形射流的侵彻性能[5-7]，但未对环形射流的成型和侵彻过程进行深入分析。

环形射流的研究起步较晚，相关理论基础比较薄弱。利用数值模拟研究这类复杂的聚能装药问题，可以得到一些试验无法观测到的现象。本文运用显式动力学有限元软件LS-DYNA，对环向多点同步起爆条件下装药爆轰波的传播规律、环形药形罩在爆轰波作用下的成型过程及环形射流对靶板的侵彻效应进行了数值模拟，并分析了起爆点数对环形射流侵彻能力的影响。

1 计算模型

1.1 环形聚能装药结构

环形聚能装药主要由药型罩、装药及壳体3部分组成。环形聚能装药结构及药形罩结构如图1所示。其中，药罩口径d为80 mm；药形罩锥角α为60°，药型罩壁厚δ为4 mm；环形药型罩对称面的半径R0为160 mm，药型罩外径Router为200 mm，药型罩内径Rinner为120 mm，壳体厚度a为2 mm，装药高度H为160 mm，炸高为80 mm。

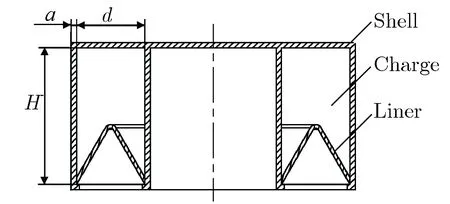
图1 环形聚能装药结构及药型罩结构示意图Fig.1 Schematic diagrams of the annular shaped charge and the liner

1.2 有限元模型

有限元模型主要由药型罩、装药、壳体、空气以及靶板5部分组成，如图2所示。靶板厚100 mm，材料为921A船用钢板。其中，壳体和靶板采用Lagrange单元离散，药型罩、装药和空气则采用ALE单元离散，两种网格之间采用流固耦合算法。

图2 环形聚能装药有限元模型Fig.2 Finite-element model of the annular shaped charge and target

使用solid164实体单元对模型进行划分，将药型罩、装药和空气划分为共节点单元网格，空气网格包围药型罩和装药，并延伸至射流运动的整个区域。对空气网格的上下表面以及侧面添加无反射边界，模拟无限条件。靶板被侵彻区域网局部加密，设定网格特征尺寸为2 mm，以匹配药型罩网格，提高计算精度。

1.3 材料模型及其参数

本文炸药为Octol，采用HIGH_EXPLOSIVE_BURN本构方程和JWL状态方程描述其爆轰过程，炸药模型主要参数如表1所列。其中，ρ为炸药密度;D为炸药爆速;pCJ为炸药CJ压力;A，B，R1，R2，ω为JWL状态方程参数。药型罩材料选用紫铜，壳体材料选用45#钢，靶板材料为船用921A船用钢板，均采用Johnson-Cook本构模型和Gruneisen状态方程来描述冲击作用下的材料响应行为，药型罩、壳体和靶板材料模型主要参数如表2所列。其中，ρ为材料密度；E为弹性模量；G为剪切模量；ν为泊松比；Tm为融化温度；A，B，n，c，m为材料本构模型参数；C为μs-μp曲线的截距;E0为初始单位体积内能;V0为初始相对体积;S1，S2，S3，γ0，α为状态方程参数。对于多物质ALE算法而言，需建立覆盖整个侵彻体飞行区域的空气网格，空气采用NULL本构模型，状态方程为线性多项式LINEAR_POLYNOMIAL模型，空气模型主要参数如表3所列。其中，ρ为空气密度；C1，C2，C3，C4，C5，C6均为状态方程参数。

2 计算结果及分析

2.1 环向8点同步起爆过程分析

以环向8点同步起爆为例，分析装药的起爆过程。图3为爆轰波传播过程的压力等值面图。起爆后，t为0 μs时，以各起爆点为中心产生8个球面爆轰波逐渐向外传播；t为6 μs时，爆轰波波阵面传至壳体侧壁并在侧壁发生反射，壳体侧壁在一定程度上限制了爆轰波发散，增加了爆轰波的强度；t为8 μs时，环向8个爆轰波相互碰撞并在碰撞面上发生反射，此时爆轰波前沿仍为明显的波浪形；t为10 μs时，爆轰波前沿与药型罩锥角顶端接触，在药型罩材料中产生很大压力，药形罩材料开始变形；t为14 μs时，爆轰波阵面继续向下推进，同时在环向相互融合，此时爆轰波前沿变得平整；t为22 μs时，爆轰波前沿传播至药型罩底部，各爆轰波前沿基本上处于同一平面内，波浪形状消失。从上述过程可以看出：环向多点同步起爆条件下，爆轰波在各个方向上逐渐扩展、相互融合，最终形成统一的爆轰波前沿。在爆轰波与药型罩的作用过程中，起爆点下方所对应的药型罩材料最先受到挤压，因而最先被压垮；而在爆轰波阵面的碰撞面上，由于受到反射作用的影响爆轰波压力得到加强，该处药型罩材料所受到的压力最大，获得的初速度也最大。

表1 Octol的模型参数[8]Tab.1 Material parameters of Octal

表2 紫铜、45#钢和船用921A钢板的模型参数[8-9]Tab.2 Material parameters of copper, 45# steel and 921A steel

表3 空气的模型参数Tab.3 Material parameters of air

图3 环向8点同步起爆时爆轰波过程Fig.3 The propagation of detonation waves with 8-point synchronous explosive circuit

2.2 环形射流成型过程分析

图4为环形射流成型过程中头部和尾部速度变化曲线。如前所述，t为10 μs时，头部爆轰波阵面传至药型罩材料顶端，药型罩材料从顶端逐渐被压垮，向轴线方向汇聚，并在轴线方向发生碰撞，一部分材料具有正向速度向前运动成为射流头部，另一部分材料具有负向速度向后运动成为射流尾部。t为22 μs时，爆轰波阵面传至药型罩底部。在t为10～22 μs之间，药型罩材料被急剧加速，也是射流形状发生较大变化的过程，在t为24 μs时，射流头部速度达到最大值4 971 m·s-1。之后在爆轰波、爆轰波产物和射流自身速度梯度的共同作用下，射流头部速度有所下降，在t为50 μs时，速度稳定在3 860 m·s-1。与此同时，射流尾部速度逐渐提高，t约为40 μs时，尾部速度稳定在558 m·s-1。

图5为环形射流的成型过程。从图5可以看出，射流头部和尾部存在很大的速度梯度，正是该速度梯度使射流逐渐被拉伸。同时，环形射流沿环向也存在一定的速度差异，在爆轰波反射加强的位置，对应的射流头部速度最大，且在运动过程中射流头部很快被拉断，与环形射流脱离。t为50 μs时，环形射流基本成型，而其头部和尾部仍有较大的速度差，射流头部逐渐被拉断，射流的头部形状被破坏，不利于对靶板的侵彻。环形射流的成型过程与传统圆锥形药型罩射流的成型过程基本相似，但前者的形状难以保持，容易被拉断，对炸高也更为敏感。

图4 环形射流成型过程中头部和尾部速度变化Fig.4 Velocity history curves of top and caudal points of the annular jet

图5 环形射流成型过程Fig.5 The formation of the annular jet

2.3 侵彻效应分析

图6为环形射流侵彻靶板过程。从图6可以看出，t为50 μs时，虽然射流头部未接触靶板，然而在爆轰波、爆轰产物和空气共同作用下，靶板中已经产生了较大的应力。t为60 μs时，射流头部与靶板接触，射流头部的速度非常高，在碰撞点附近形成了一个高温、高压、高应变率的区域，在靶板中产生很强的应力波，射流头部开始侵入靶板，此阶段称为射流侵彻的开坑阶段。t为70 μs时，射流进一步侵入靶板，应力波以射流头部为中心，向靶板内传播，波阵面近似为半球形；t为80 μs时，应力波波阵面传至靶板背面，并在靶板背面产生反射拉伸波；t为90 μs时，应力波在靶板内进一步传播，射流尾部发生断裂；t为100 μs时，应力波经过多次反射叠加，在靶板内应力逐渐趋于均匀，射流尾部完全断开；t为150 μs时，射流主体已经基本完成侵彻过程。t在70～150 μs之间，环形射流持续侵彻靶板，形成环形弹坑，此阶段称为射流侵彻的扩展阶段，该阶段侵深稳定增加，侵彻孔径变化不大，射流速度降低、头部磨蚀，质量、能量逐渐消耗。t为150～250 μs时，是射流侵彻的终止阶段，随着射流速度的降低和射流尾部逐渐断裂，其侵彻能力大幅下降，靶板强度的作用愈来愈明显。后续射流推不开前面已经释放能量的射流残渣，随着残渣越积越厚，射流破甲过程停止。在射流的撞击下，靶板背面产生隆起变形，在侵彻孔洞下方的靶板材料中产生了很大的剪切应力。

图6 环形射流侵彻靶板过程Fig.6 Penetration process of the annular jet into the target

本算例中由于剩余靶板较厚，能够抵抗该剪切作用，可以预见，如果剩余靶板较薄，不能抵抗该剪切作用，靶板将在此处被剪切破坏，形成圆形冲塞块。此阶段称为射流侵彻的冲塞阶段。如上所述，环形射流对靶板的破坏主要为塑性扩孔(或塑性扩孔+剪切冲塞)的形式。

图7为侵彻深度随时间的变化曲线。从图7可以看出，侵彻过程持续约200 μs，最终的侵彻深度约为52 mm。侵彻深度的增加主要发生在t为70～150 μs，且增速逐渐变慢，这主要是由于随着侵彻深度的增加，射流速度降低、质量减少，因而侵彻能力逐渐降低。尤其是t为150 μs以后，由于射流残渣在侵彻弹坑内堆积，使得侵彻深度增加非常缓慢。

图7 侵彻深度随时间变化曲线Fig.7 The history curve of penetration depth

图8为侵彻完成时，靶板的侧视图和俯视图。从侧视图可以看出，靶板塑性变形区域主要集中在弹坑附近，其余部分没有出现明显的塑性变形。弹坑口部有轻微翻起的唇边，这是由于射流挤压靶板材料，使弹坑入口处靶板材料反向流动、在表面堆积造成的。弹坑从口部到底部有向外扩展的趋势，底部由于射流残渣的堆积，其宽度大于口部。从俯视图中可以看出，塑性变形区域近似为八边形(以8个

起爆点对应位置为顶点)，环形射流形成的弹坑接近圆形，孔径与环形药型罩对称面直径相当，可以达到对靶板进行圆形开孔的目的。

(a) Side view

(b) Top view 图8 侵彻完成时靶板侧视及俯视图Fig.8 The side and top views of the target after penetration

3 起爆点数对环形射流侵彻能力的影响

如前所述，环向多点同步起爆条件下，爆轰波前沿到达药形罩顶端的时间沿环向并不同步，压力大小也不一致，这是环向多点同步起爆的特点。为了研究起爆点数对环形射流侵彻能力的影响，对环向4点、6点、8点、10点、12点、14点以及16点同步起爆条件下的射流成型及侵彻过程进行了数值仿真。图9为不同起爆点数下，爆轰波到达药形罩顶端时刻的前沿形状。可以看出，爆轰波在传播过程中相互融合形成统一前沿，起爆点数越多，爆轰波前沿越接近平面，到达药形罩顶端的时间差异越小，即药形罩的压垮过程同步性越好。

图9 不同起爆点数下的爆轰波前沿形状

图10为环形射流的侵彻深度随起爆点数变化情况。从图10可以看出，环形射流的侵彻深度随起爆点数的增加而增大，但并非呈线性关系。起爆点数从4点增加到10点的过程中，侵彻深度由42 mm大幅增加至60 mm，增幅约43%；而起爆点数从10点增加到16点的过程中，侵彻深度由60 mm增加至64 mm，增幅明显减小，仅约7%。从理论上讲，起爆点数越多，环形射流侵彻能力越强，但增加起爆点个数也会增加同步起爆网络的级数和复杂程度，导致其输出同步性时间偏差增大，这将对环形射流的成型产生不利影响[10-11]。实际使用过程中，在保证成型效果的基础上，应尽可能减少起爆点数，建议选择10点同步起爆网络。本文所研究的环形聚能装药结构在10点同步起爆条件下，炸高为1倍装药口径时,侵彻深度为装药口径的0.75倍。

图10 环形射流侵彻深度随起爆点数的变化Fig.10 Penetration depth of the annular jet varies with the number of detonation points

4 结论

通过对多点同步起爆条件下环形射流的成型和侵彻过程进行分析，可以得到以下结论：

1) 在环向多点同步起爆条件下，爆轰波通过相互碰撞形成统一的近似平面的爆轰波前沿，但爆轰波前沿到达药形罩顶端的时间沿环向并不同步，压力大小也不一致，起爆点下方所对应的药型罩材料最先受到挤压，因而最先被压垮；而在爆轰波阵面的碰撞面上，爆轰波压力由于反射作用得到加强，该处药型罩材料受到的压力最大，获得的初速度最大。

2) 环形射流的成型过程与传统圆锥形药型罩射流基本相似，但环形射流不仅头部和尾部存在速度梯度，而且沿环向也存在一定的速度差异，形状难以保持，容易被拉断。因此在环形射流应用过程中，应注意选择合适的炸高，以便最大程度地发挥其侵彻能力。

3) 环形射流能够实现对靶板的大口径开孔，靶板的破坏模式主要为塑性扩孔，圆形弹孔孔径与药型罩对称面直径相当。

4) 环形射流的侵彻能力随起爆点数的增加而增大，当起爆点数大于10时，侵彻深度增大幅度明显减小，建议选择10点同步起爆网络。

环形射流侵彻能力的影响因素很多，下一步将开展环形聚能装药的结构优化设计，提高其侵彻能力。

[1]CHICK M C, BUSSELL T J. Development of a coolie cutter explosively formed projectile[C]// 17th International Symposium on Ballistics. Midrand, South Africa, 1998: 167-174.

[2]王成, 宁建国, 卢捷. 环形射流形成及侵彻的数值方法研究[J]. 北京大学学报：自然科学版，2003, 39(3): 316-321.(WANG Cheng, NING Jian-guo, LU Jie. Study on numerical simulation of the annular jet formation and penetration[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2003, 39(3): 316-321.)

[3]王成, 恽寿榕, 黄风雷. W型聚能装药射流形成及侵彻的实验和数值仿真研究[J]. 兵工学报, 2003, 24(4): 451-454.(WANG Cheng, YUN Shou-rong, HUANG Feng-lei. An experimental study and numerical simulation on annular jet formation and penetration[J]. Acta Armamentarii, 2003, 24(4): 451-454.)

[4]吴成, 曾艳春, 张向荣, 等. 环型聚能药型罩的设计新方法与实验[J]. 北京理工大学学报, 2007, 27(4): 291-294.(WU Cheng, ZENG Yan-chun, ZHANG Xiang-rong, et al. Investigation and design on the penetration effect of annular-linear shaped charge[J]. Transactions of Beijing Institute of Technology, 2007, 27(4): 291-294. )

[5]李永胜, 王伟力, 姜涛. 用于串联战斗部的环形切割器优化设计[J]. 弹箭与制导学报, 2010, 30(2): 93-96.(LI Yong-sheng, WANG Wei-li, JIANG Tao. Optimum design on annular cutter of tandem warhead[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(2): 93-96.)

[6]李永胜, 王伟力, 刘晓红, 等. 串联战斗部前级的环形切割器优化设计[J]. 工程爆破, 2011, 17(4): 1-4.(LI Yong-sheng, WANG Wei-li, LIU Xiao-hong, et al. Design optimization on annular cutter in the front of tandem warhead[J]. Engineering Blasting, 2011, 17(4): 1-4.)

[7]李永胜, 王伟力, 田传勇. 环形切割器药型罩方案优化设计[J]. 弹箭与制导学报, 2011, 31(4): 118-120.(LI Yong-sheng, WANG Wei-li, TIAN Chuan-yong. The optimization design for the liner of annular cutter[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(4): 118-120.)

[8] 黄群涛, 李铁鹏, 钱建平, 等. 环形EFP成型及侵彻过程的数值模拟[J]. 火炸药学报, 2009, 32(5): 50-53.(HUANG Qun-tao, LI Tie-peng, QIAN Jian-ping, et al. Numerical simulation on forming and penetration process of annular EFP[J]. Chinese Journal of Explosives & Propellants, 2009, 32(5): 50-53.)

[9] 李继承, 陈小伟, 陈刚. 921A钢纯剪切帽状试件绝热剪切变形的数值模拟[J]. 爆炸与冲击, 2010, 30(4): 361-369.(LI Ji-cheng, CHEN Xiao-wei, CHEN Gang. Numerical simulations on adiabatic shear deformations of 921A steel pure shear hat-shaped specimens[J]. Explosion and Shock Waves, 2010, 30(4): 361-369.)

[10] 温玉全, 焦清介, 李国新, 等. 刚性面同步起爆网络设计及同步时间分析[J]. 兵工学报, 2001, 22(1): 45-47.(WEN Yu-quan, JIAO Qing-jie, LI Guo-xin, et al. Structural design and time analysis of synchronous explosive circuit in a rigid surface[J]. Acta Armamentarii, 2001, 22(1): 45-47.)

[11] 胡双启, 邰玲, 曹雄. 环形传爆药多点同步起爆网络的应用研究[J]. 火炸药学报, 2004, 27(3): 62-65.(HU Shuang-qi, TAI Ling, CAO Xiong. Application of multi-point synchronous explosive logic circuit of the ring propagating charge[J]. Chinese Journal of Explosives & Propellants, 2004, 27(3): 62-65.)