轴向输出线极化TE11同轴波导模式 相对论磁控管的粒子模拟研究
2018-07-09史迪夫钱宝良王弘刚杜广星
史迪夫, 钱宝良, 王弘刚, 李 伟, 杜广星
(国防科技大学 前沿交叉学科学院, 长沙 410073)
具有高斯波形的高功率微波已广泛应用于民用和军用领域[1]。与其他波导模式相比,TEM模式,线极化TE11模式,圆极化TE11模式均可高效直接地通过相应的天线辐射出高质量的高斯波形微波。根据前人的研究,相对论磁控管(RM)可单独产生不同的波导模式,例如矩波导中的TE10模式[2-3]、圆波导中的TE01模式[4-5]、线极化TEn1(n≥1)模式[4-8]及圆极化TEn1(n≥2)模式[7-10]。直到2012年,美国空军研究实验室提出了一种具有全腔提取结构的RM[11],相关研究[12-14]表明,该RM可在同轴波导中单独产生TEM模式、线极化TEn1(n≥1)模式及圆极化TEn1(n≥1)模式。但是根据理论分析[12],若要产生线极化TE11同轴波导模式,该RM必须在谐振腔数为4、电子轮辐数为1或3的情况下才能实现。而另一方面,由于4腔的谐振腔结构具有较强的模式隔离度和角向偶对称性,在模拟或实验中都很难产生1或3个电子轮辐数,因此具有全腔提取结构的RM难以产生线极化TE11同轴波导模式。为了产生线极化TE11同轴波导模式,本文提出了一种新型输出结构,该结构不仅能更容易地实现线极化TE11同轴波导模式的微波输出,而且在此基础上能更容易地实现更高频段RM的设计。
1 结构设计与分析
文献[12]指出,具有全腔提取结构的RM在输出同轴波导中产生TEM模式,左旋圆极化TEn1模式和右旋圆极化TEn1模式的必要条件分别为
(1)
式中,n0为电子轮辐数;N≥4为谐振腔总数;nL和nR分别为左旋和右旋圆极化模式的角向模式数,Z
为整数集。若要该结构的RM产生线极化TE11同轴波导模式,则需满足
nL=nR=1
(2)
因此,由式(1)和式(2)可知,产生线极化TE11同轴波导模式的必要条件为
(3)
但是,一般而言,电子轮辐数都不多于谐振腔总数,即n0≤N,并且由于4腔的谐振腔结构具有较强的模式隔离度和角向偶对称性,在模拟或实验中都很难产生1或3个电子轮辐数,因此具有全腔提取结构的RM难以产生线极化TE11同轴波导模式。
此外,由RM的束波相互作用原理可知,n号振荡模式的行波沿阳极内表面行进的相速vp必须小于光速c[15],即
(4)
式中,Ra为阳极半径;ωn为n号振荡模式的角频率。事实上,振荡模式号数n即为电子轮辐数n0,它表示束波互作用区内电磁场分布的角向周期数。若假设具有全腔提取结构的4腔RM能够产生1或3个电子轮辐,输出线极化TE11同轴波导模式,且假设Ra=18 mm,则由式(4)可知,n号振荡模式频率fn的上限为
(5)
从式(5)可以看出,若保持阳极半径不变,该结构的RM具有一个频率上限。比如当阳极半径为18 mm时,频率上限为7.96 GHz。因此,具有全腔提取结构的RM即使能够产生线极化TE11同轴波导模式,也难以实现更高频段RM的设计。
基于以上分析和判断,针对全腔提取结构的不足,下面以一个谐振腔数为10的RM为例,对其输出结构进行设计和分析。该RM的纵剖面和横剖面分别如图1和图2所示。

图1 RM的纵剖面图 Fig.1 Schematic diagram of the longitudinal profile of the RM

(a) S1 plane
(b) S2 plane

(d) S4 plane
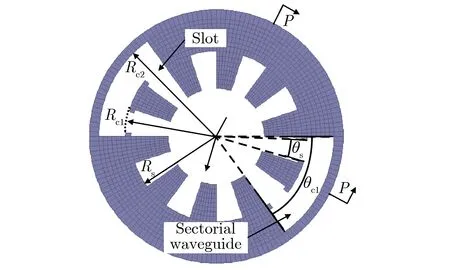
从图2可以看到,整个RM的结构被划分为4个部分,即部分A:用于电功率输入的同轴波导;部分B:用于束波相互作用的谐振腔结构;部分C:用于微波提取的扇形波导;部分D:用于微波输出的同轴波导。该RM的结构参数如表1所列。

表1 RM的结构参数Tab.1 Structure parameters of the RM
如图3(a)所示,该RM的10个谐振腔依次标记为1-10,2个扇形波导依次标记为I和II,与传统RM一样,该RM容易工作在π模式上,形成5个均匀的电子轮辐,这表明相邻两谐振腔中的电磁场均具有相同的幅值和180°的相位差。由于对部分C的扇形波导和部分D的同轴波导的横截面尺寸均有限制,因此对于4.38 GHz的目标工作频率而言,在扇形波导中将只有TE11模式能稳定传输,在同轴波导输入端中将只有TEM,TE11,TE21,TE31模式能稳定传输,而在同轴波导输出端中将只有TEM,TE11,TE21模式能稳定传输。
已有的研究[16]表明,谐振腔中最低阶的角向模式对束波相互作用起着决定性的作用,因此在谐振腔内主要存在角向电场,如图3(b)所示。如图3所示,谐振腔1和2中的角向电场将通过一个90°的弯曲波导后,转换成扇形波导I中的TE11模式的径向电场。由于这两个角向电场具有相同的幅值和180°的相位差,且相对应的模式耦合结构具有左右对称性,因而这两个角向电场转换成扇形波导I中的径向电场后具有相同的幅值和相位。同理,谐振腔6和7中的角向电场转换成扇形波导II中的径向电场后也具有相同的幅值和相位。但是由于谐振腔1和6以及谐振腔2和7中的角向电场相位均相差180°,因而在扇形波导I和扇形波导II中激励起的径向电场相位也将相差180°。这一特性为后续产生线极化 TE11同轴波导模式提供了必要条件。另外,根据模式激励的相关理论[12],在部分C的扇形波导的输出端,即部分D的同轴波导的输入端,除激励起线极化TE11同轴波导模式外,还将激励起线极化TE31同轴波导模式。因此,为了抑制TE31模式,输出纯净的TE11模式,需缩小部分D的同轴波导的横截面尺寸,将TE31模式截止。

(a) S2 plane with electron spokes

(b) S1 plane with electric field distribution

(c) S2 plane with electric field distribution
此外,若假设具有该新型输出结构的10腔RM能够产生5个电子轮辐,输出线极化TE11同轴波导模式,且假设Ra=18 mm,则由式(5)可知,5号振荡模式(π模)频率f5的上限为
(6)
对比式(5)和式(6)可以看出,若保持阳极半径Ra=18 mm不变,具有该新型输出结构的10腔RM的频率上限为13.26 GHz,这明显高于具有全腔提取结构的RM的频率上限7.96 GHz,并且随着谐振腔总数N(N=4k+2,k为非负整数)的增加和电子轮辐数n0(n0=N/2)的增加,该RM的频率上限还可进一步提高。
通过以上结构设计与分析可以看出,与全腔提取结构相比,本文设计的新型输出结构,不仅能更容易地实现线极化TE11同轴波导模式的微波输出,而且在此基础上能更容易地实现更高频段RM的设计。下面通过粒子模拟研究来加以分析和证明。
2 粒子模拟与分析
利用三维粒子模拟软件CHIPIC[17],对建立的的10腔RM模型结构的工作性能进行了模拟与分析。在模型计算中,外加电压在3 ns后保持在220 kV,持续时间为40 ns,外加轴向磁场在束波互作用区内为0.4 T,模拟结果如图4所示,电子束与辐射模式分布如图5所示。

(a) Input electron beam power vs. time

(b) Output microwave power vs. time

(c) Amplitude of electric field integral in the resonant cavity from 0 to 40 ns

(d) Spectrums of electric field integral in the resonant cavity from 0 to 40 ns
图4(a)和图4(b)表明输入电功率和输出微波功率分别为446 MW和208 MW,相应的功率转换效率达到46.6%,且微波饱和时间约为12 ns。图4(c)和图4(d)分别表示0~40 ns时间内谐振腔内电场积分幅值及其相应频谱。从图4(d)中可以看出,在频率4.38 GHz和8.76 GHz处有两个明显的峰值,它们分别对应π模的基模频率和π模的二次谐波频率。除了这两个峰值外,在频率5.38 GHz和6.12 GHz处还有两个较小的峰值,它们应对应着π模的高阶轴向模式[18]。然而,与π模的基模频率相比,其他频率的幅值由于太小通常可忽略其影响。

(a) Electron spokes in the Rθ plane of the RM

(b) Electron spokes in the RZ plane of the RM

(c) Output mode in the output port at 20 ns
图5电子束与辐射模式分布
Fig.5Distributionsofelectronsandradiatedmode
图5(a)和图5(b)分别表示20 ns时在Rθ和RZ平面上RM中的电子轮辐状态。容易看出,在10腔RM中的角向方向上形成了5个均匀的电子轮辐。根据第1节的分析,该电子轮辐状态的形成为后续产生线极化TE11同轴波导模式提供了必要条件。此外,电子束在轴向方向上也能较好地被约束在束波互作用区内,这表明束波相互作用主要发生在图1中所示的谐振腔互作用区内,而在谐振腔传输区内几乎不会发生。因而用于微波提取与传输的谐振腔传输区对RM谐振系统的等效电路几乎没有影响,所以,RM的工作性能如谐振频率,对传输区结构的扰动如耦合口结构,是不敏感的。与传统全腔提取结构[11]相比,该结构的改进使影响RM工作性能的敏感性参数减少,从而有利于RM的优化设计与稳定运行。图5(c)表明输出同轴波导中的微波主要为线极化TE11模式,尽管该输出口对TEM和TE21模式也不截止,但它们在模拟中并未被明显观测到。
3 结论
针对全腔提取结构难以产生线极化TE11同轴波导模式问题,提出了一种用于RM中轴向输出线极化TE11同轴波导模式的新型输出结构,该结构不仅能更容易地实现线极化TE11同轴波导模式的微波输出,而且在此基础上能更容易地实现更高频段RM的设计。粒子模拟表明,当该器件的工作频率为4.38 GHz,输出功率为208 MW时,功率转换效率可达到46.6 %。
[1]BARKER R J, SCHAMILOGLU E. High Power Microwave Sources and Technologies[M]. Hoboken, NJ: Wiley, 2001.
[2]LI T, LI J, HU B. Studies of the frequency-agile relativistic magnetron[J]. IEEE Trans Plasma Sci, 2012, 40(5): 1 344-1 349.
[3]SHI D F, QIAN B L, WANG H G, et al. A compact mode conversion configuration in relativistic magnetron with a TE10output mode[J]. IEEE Trans Plasma Sci, 2015, 43(10): 3 512 -3 516.
[4]FUKS M I, KOVALEV N F, ANDREEV A D, et al. Mode conversion in a magnetron with axial extraction of radiation[J]. IEEE Trans Plasma Sci, 2006, 34(3): 620-626.
[5]LI W, LIU Y G, ZHANG J, et al. Experimental investigations on the relations between configurations and radiation patterns of a relativistic magnetron with diffraction output[J]. J Appl Phys, 2013, 113(2): 023304.
[6]SHI D F, QIAN B L, WANG H G, et al. A novel TE11mode axial output structure for a compact relativistic magnetron[J]. J Phys D: Appl Phys, 2016, 49(13): 135103.
[7]FUKS M I, SCHAMILOGLU E. 70% efficient relativistic magnetron with axial extraction of radiation through a horn antenna[J]. IEEE Trans Plasma Sci, 2010, 38(6): 1 302-1 312.
[8]LIU M, FUKS M I, SCHAMILOGLU E, et al. Operation characteristics of A6 relativistic magnetron using single-stepped cavities with axial extraction[J]. IEEE Trans Plasma Sci, 2014, 42(10): 3 344-3 348.
[9] LIU M, LIU C, FUKS M I, et al. Operation characteristics of 12-cavity relativistic magnetron with single-stepped cavities[J]. IEEE Trans Plasma Sci, 2014, 42(10): 3 283-3 287.
[10] LIU M, FUKS M I, SCHAMILOGLU E, et al. Frequency switching in a 12-cavity relativistic magnetron with axial extraction of radiation[J]. IEEE Trans Plasma Sci, 2012, 40(6): 1 569-1 574.
[11] HOFF B W, GREENWOOD A D, MARDAHL P J, et al. All cavity-magnetron axial extraction technique[J]. IEEE Trans Plasma Sci, 2012, 40(11): 3 046-3 051.
[12] SHI D F, QIAN B L, WANG H G, et al. Theoretical investigations on radiation generation of TEM linearly or circularly polarized TEn1coaxial waveguide mode in relativistic magnetron[J]. Sci Rep-UK, 2017, 7: 1 491.
[13] SHI D F, QIAN B L, WANG H G, et al. A novel relativistic magnetron with circularly polarized TE11coaxial waveguide mode[J]. J Phys D: Appl Phys, 2016, 49(46): 465104.
[14] SHI D F, QIAN B L, WANG H G, et al. A modified relativistic magnetron with TEM output mode[J]. Phys Plasmas, 2017, 24(1): 013118.
[15] 王文祥. 微波工程技术[M]. 北京: 国防工业出版社, 2009. (WANG Wen-xiang. Microwave Engineering Technology[M]. Beijing: National Defense Industry Press, 2009.)
[16] UHM H S. A kinetic theory of the extraordinary mode perturbations in cylindrical relativistic magnetrons[J]. Phys Fluids B, 1992, 4(3): 740-749.
[17] ZHOU J, LIU D, LIAO C, et al. CHIPIC: An efficient code for electromagnetic PIC modeling and simulation[J]. IEEE Trans Plasma Sci, 2009, 37(10): 2 002-2 011.
[18] VERMA R K, MAURYA S, SINGH V V P. Study of mode control in long-anode high-power pulse magnetron[J]. IEEE Trans Plasma Sci, 2014, 42(12): 4 010-4 014.
