基于AHP的学习习惯对中学生学习成绩的影响

2018-07-09侯海凤

珠江教育论坛 2018年2期

侯海凤

（肇庆市端州中学,广东肇庆 526040）

一、概论

关鸿宇[1]教授说：“习惯是一种顽强的、巨大的力量，它可以主宰人的一生。”叶圣陶先生强调：“教育，往简单方面说，只需一句话，就是养成良好习惯。”[2]孔子曰：“少成若天性，习惯成自然。”[3]也就是说少年时期养成的习惯最终会固化成性格。一位著名行为主义者[3]提出了学习习惯说：良好学习习惯的形成也是学习的结果，好的学习习惯不仅能促进学生的学习，而且对他们的人生起着举足轻重的作用[3]。冯海英[4]认为：只有养成良好的课前准备习惯、课堂学习习惯、课后复习习惯和元认知习惯，才能取得良好的学习成绩；即拥有良好的学习习惯，对于提高学生的学习成绩非常重要。已有文献中，研究者一般通过对调查报告中的数据进行统计分析，从而获得中学生的学习习惯对学习效果的影响，但没有分析课前准备习惯、课堂学习习惯、课后复习习惯和作业与考试习惯这4个方面对中学生学习影响的大小。本文中，笔者采用层次分析法建立模型，分析了课前准备习惯、课堂学习习惯、课后复习习惯与作业和考试习惯这几个方面对中学生学习成绩的影响，旨在为教育工作者培养学生良好的学习习惯提供参考和借鉴。

二、层次分析法

（一）概述

层次分析法[5-6]（英文简称AHP）是将与决策相关的元素分解成目标、准则、方案等层次，并对这些层次进行定性和定量分析的决策方法。层次分析法有许多优良特质，主要归结如下：（1）AHP是一种定性与定量分析相结合的研究方法，能处理很多最优化技术也无法解决的实际问题；（2）AHP的定量数据并不多，但能透彻地探索问题的本质；（3）AHP的原理很容易被人们(甚至文科出身的人)所掌握；（4）AHP使得决策者和决策分析者能够相互沟通，因此增加了决策的有效性。

（二）层次分析法的步骤

1.构造层次结构

找出实际问题的全部影响因素，根据选取的准则将这些因素分解成若干层次，同一层因素从属于上一层的因素，同时支配下一层的因素[6].确定层次结构是AHP的基础.

2.构造判断矩阵

采用萨迪等人[5]提出的一致矩阵法构建判断矩阵R[7]，矩阵元素的比例标度如表1所示。

表1 判断矩阵元素的比例标度

其中 aji=1/aij,i≠j。

3.计算权向量和检验一致性

采用公式(1)～(6)检验判断矩阵R的最大特征根.若通过检验，可以作为权向量；否则，需要重新构造判断矩阵[7].具体步骤如下：

（1）采用公式(1)归一化R的每一列。

（2）采用公式(2)求[Wij]的行和

（3）采用公式(3)归一化 [Wi]，

（4）采用公式(4)计算判断矩阵R的最大特征值λ。

（5）采用公式(5)对λ做一致性检验。当P＜0.1时，则判断矩阵R的特征向量可作为权向量．

其中：I是一致性指标，S称为随机一致性指标[8]，其值如表2

3.计算权向量和检验一致性

表2 随机一致性指标S的数值

三、建立基于层次分析法的学习习惯对中学生学习成绩的影响模型

（一）构造层次结构

本文采用文献[9]的方法对学习习惯进行分类，将学习习惯分为4类：课前预习习惯(B1)，课堂学习习惯(B2)，课后复习习惯(B3)，作业和考试习惯(B4)。课前预习习惯包括学习计划(C11)和预习(C12)2个指标；课堂学习习惯包括课堂听课(C21)、课堂笔记(C22)和举手发言(C23)3个指标；课后复习习惯包括反思总结(C31)和看参考书(C32)2个指标；作业和考试习惯包括课后作业(C41)、作业改正(C42)和考试总结(C43)3个指标。本文给出的中学生学习习惯层次结构如图1所示。

图1 中学生学习习惯层次结构图

（二）构造判断矩阵

根据图1的层次结构图构建5个相应的判断矩阵[3]，即一级指标(学习习惯对学习成绩的影响A)的判断矩阵RA,二级指标课前预习习惯的判断矩阵R课前预习习惯B1,简记为RB1;类似定义余下的3个二级指标的判断矩阵分别为RB2、RB3和RB4。在课前预习习惯、课堂学习习惯、课后复习习惯、作业和考试习惯4个指标中，笔者认为课堂学习习惯指标比课前预习习惯指标的影响强，比课后复习习惯指标的影响稍强，比作业和考试习惯指标影响略强。根据表1的标度方法，对判断矩阵RA中的元素赋值如下：RA(2,1)=5,RA(3,1)=2,RA(4,1)=4,RA(2,3)=3,RA(2,4)=2,RA(3,4)=1/2。在学习计划和预习2个指标中，笔者认为学习计划比预习影响稍强，所以RB1(1,2)=3。在课堂听课、课堂笔记和举手发言3个指标中，笔者认为课堂听课和举手发言比课堂笔记影响强，而举手发言比课堂听课影响稍强。根据表1的标度方法，对判断矩阵RB2中的元素赋值如下：RB2(1,2)=3,RB2(1,3)=2,RB2(2,3)=1/2。在反思总结和看参考书2个指标中，笔者认为反思总结比看参考书影响强，所以RB3(1,2)=3。在课后作业、作业改正和考试总结3个指标中，笔者认为课后作业比作业改正的影响稍强，而比考试总结的影响强。这5个判断矩阵具体如下所示。

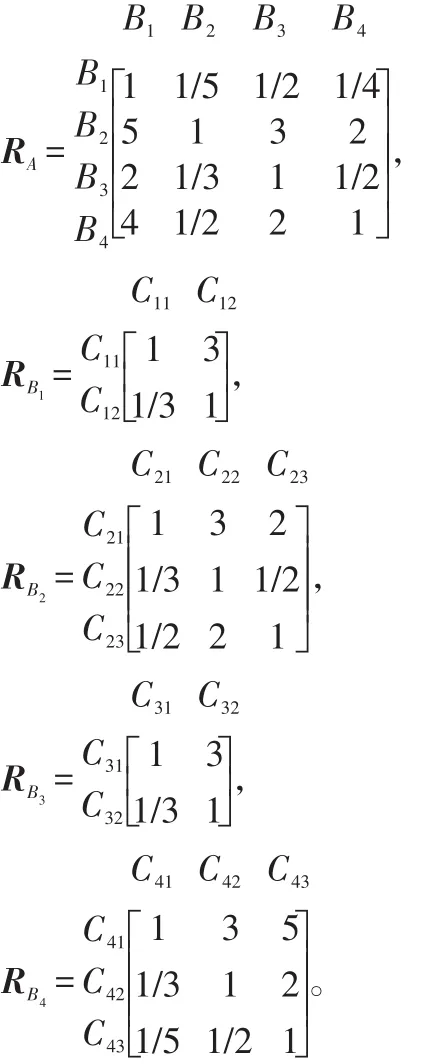
（三）归一化判断矩阵

根据公式（1），对5个判断矩阵进行归一化，变化后的矩阵仍采用原来的矩阵表示。

（四）计算权向量

根据公式（2）和公式(3)计算后的归一化向量如下所示：

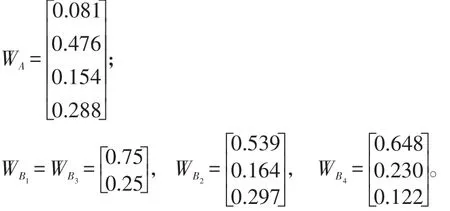
（五）计算最大特征根及其一致性检验

根据公式(4)计算判断矩阵RA的最大特征根λA=4.043。类似计算

由于和为2阶矩阵，且2阶矩阵总是一致阵，因此不必验证其一致性[10]，而剩余的3个判断矩阵RA、RB2和RB4，根据公式(5)和(6)计算可得如下结果：

由于,所以一致性检验通过，上述特征向量可作为权向量．

基于层次分析法的学习习惯对中学生学习成绩影响模型的各变量系数如下：

因此本文建立的模型可为

模型中各系数的大小，反映了该学习习惯对中学生学习成绩的影响程度，系数大于0.1的指标有课堂听课、举手发言、反思总结和课后作业，这说明该模型分析的结论是教师在教学过程中，要引导学生认真听课、积极思考，鼓励学生参与讨论，积极回答问题，课后多思考以及认真做作业。

四、模型检验

为了验证上述模型的准确性，笔者根据图1中的指标制作了调查问卷，并向肇庆市某普通中学2个班共88名学生进行了调查。先将调查问卷中每一题的“A”“B”“C”“D”4个选项转化成得分数，如某题的选项“A”=90分，“B”=80分，“C”=70分，“D”=60分；再利用建立的模型计算每个同学的预测分数，如表3所示；之后，对88名学生每人高一第一学期的期中、期末以及第二学期的期中考试成绩求平均分，并根据平均分进行排名，模型预测分数排名和平均分的排名情况如表4所示；最后，采用SPSS中的配对t检验对模型预测分数进行排名，并对平均分排名进行检验。检验结果显示，两种排名没有显著差异，这说明模型能够较好地揭示学习习惯与学习成绩之间的规律。