创设数学问题情境的有效教学策略

林卫文

（肇庆市高要区大湾镇初级中学，广东 肇庆 526119）

“学起于思，思源于疑”，“问题”是激活或唤醒思维的刺激因素。所谓创设数学问题情境，是指教师有目的、有意识地将问题寓于学生熟悉的情境中，以具体情境为载体，将抽象的数学知识具体化，使学生更容易理解与接受，让学生有明确的探究目标，从而产生强烈的探究欲望。创设数学问题情境，是数学探究教学的第一步，也是最关键的一步。下面笔者结合教学实践，提出几种创设数学问题情境的有效教学策略。

一、创设生活性的问题情境，让学生体会到数学就在身边

《数学课程标准》指出：“教学中应当努力创设源于学生生活的现实情境。好的‘现实情境’，应当是学生熟悉的、简明的、有利于引向数学本质的、真实或合理的。”笔者在平时的教学中，比较注意创设与学生的生活实际相联系的问题情境，让学生体会到生活离不开数学，数学离不开生活，让学生感受到学习数学的乐趣，从而积极主动地探索并解决问题。

情境1在探究线段的垂直平分线的性质及判定时，先设置这样一个问题情境：如图1，国庆文艺晚会上，甲、乙两位同学分别在A、B两个位置玩抢气球游戏，如果你负责放气球，气球放在直线PQ的什么位置，对甲、乙两位同学才公平？

学生被这一鲜活的生活情境深深吸引，从而主动积极地探索发现问题：到A、B两点距离相等的点在哪里？先连结AB,再作AB的垂直平分线交PQ于点P,则点P就是到A、B两点距离相等的点。

通过创设生活性问题情境，能够让学生感受到数学就在我们身边，生活中处处有数学，从而使学生将数学学习作为一种乐趣、一种渴望，从中学到丰富的数学知识。

二、创设趣味性的问题情境，提高学生学习数学的兴趣

图1 示意图

伟大的科学家爱因斯坦说过：“兴趣是最好的老师。”问题情境的创设要针对学生的年龄特点和认知规律，以激发学生的学习兴趣为出发点。初中生好奇心强，若教师能结合探究内容，将数学问题融于一些学生喜闻乐见的情境之中，就能诱发学生积极探究的欲望。

情境2在探究圆周角定理时，先播放一段精彩的足球比赛录像，使学生犹如“身临其境”，然后让学生思考下列问题：如图2，在足球比赛场上，甲、乙两名队员互相配合向对方球门PQ进攻，当甲带球到A点时，乙已跟随冲到B点，从数学角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？给出答案并说明理由。

有趣的情境设置使同学们展开热烈的讨论，然后进行探索，射门是否合适取决于射门角度的大小（如图3），过点P、Q、B作圆弧，可知在B点射门更合适，即让乙射门为好。

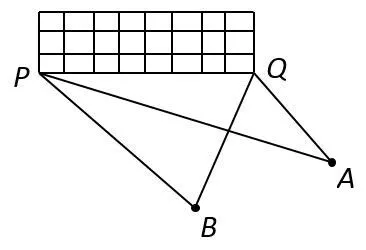
图2 示意图

图3 示意图

数学课不可避免地存在缺乏趣味性的内容，若教师只会照本宣科，则学生听来索然寡味。若教师能有意识地创设趣味性问题情境，让学生带着浓厚的兴趣进行积极思维，就能使学生变被动学习为主动学习。

三、创设实验性问题情境，培养学生的推理能力

在数学课堂教学中，可以运用教具、学具、多媒体进行模拟演示，或直接由学生参与实验创设情境，让学生动起来，从而使其实现具体思维向抽象思维的过渡，从感性认识到理性认识的升华。

情境3在探究勾股定理时，设置拼图实验，通过拼图找出直角三角形中a、b、c三边的关系。

（1）实验器材：4张如图4的全等直角三角形纸片。

（2）提示问题：用“面积法”证明，“面积法”的实质是同一图形面积用两种不同的方法计算，结果相同。

学生通过对一个直角三角形三边的长度量度、猜测，发现：32+42=52，52+122=132等规律，经过讨论，一致猜测任何直角三角形都有这种规律：a2+b2=c2。学生经过操作，尝试后发现要找出a、b、c三边关系，显然要使a、b、c都参与到面积计算中，需要大家积极思考如何拼？学生通过合作交流，很快便有了结果。学生代表上台展示结果，如图5和图6所示。

图4 示意图

图5 示意图

图6 示意图

图5 解释：大正方形边长(a+b),小正方形边长c,则

图6解释：大正方形边长c,小正方形边长(a-b)，则

学生探索了4 000多年前我国赫赫有名的重大发现——勾股定理，进一步激发了学生的民族自豪感和成就感，让学生充分体验到探索创新所带来的成功喜悦，进而产生求知欲，增加了学习兴趣，使课堂气氛更加活跃，学习效果倍增。

四、创设类比性问题情境，培养学生构建数学知识的能力

古希腊哲学家普多塔戈说过：“人脑不是一个可灌输知识的容器,而是一个可以点燃的火把。”教师先引导学生复习回忆已学过的知识，然后创设类比发现的问题情景，让学生的思维活跃起来，对所学知识产生极大兴趣，这样他们就会主动进行探索，从中理解概念，掌握规律。如此一来，新的数学知识容易在学生原有的认知结构中得以同化与构建。

情境4在探究一元一次不等式的解法时，先让学生解一元一次方程：

解 去分母：4x-10-18=9x-3，

移项：4x-9x=10+18-3，

合并同类项：-5x=25，

方程两边都除以-5：x=-5。

然后让学生尝试解不等式：

解 去分母：4x-10-18＞9x-3，

移项：4x-9x＞10+18-3，

合并同类项：-5x＞25，

不等式两边都除以-5：x＜-5。

学生通过对新旧知识进行比较，对比一元一次方程和一元一次不等式的解法，了解了不等式两边除以负数时要改变不等号的方向这一特殊情况，学生对此印象深刻，从而很好地掌握了一元一次不等式的解法。创设类比性问题情境，能使学生将已有数学知识转化到新领域中，促进了知识和能力的正迁移。

五、创设悬念性问题情境，培养学生运用数学知识解决问题的能力

古希腊教育家亚里斯多德曾说：“思维自惊奇和疑问开始。”学生都有追根求源的心理特点，通过创设悬念性的问题情境，引发学生思考，激发其好奇心，使数学知识能紧紧扣住学生的心弦，让学生能想方设法运用数学知识解决问题，促使他们自主地参与到探究活动中。

情境5探究一次函数的应用时，创设情境：假如班主任准备组织班级同学到广州旅游，咨询了两间旅行社，甲旅行社说：“如果班主任买全票，则其余学生可享受半价优惠”；乙旅行社说：“包括班主任在内全部按全票的6折优惠。”若全票价为每张240元，你们认为选择哪一家旅行社更合算？

学生们的探究欲望大增，学习兴趣高涨，小组讨论热烈，有的学生认为“甲旅行社学生可享受半价优惠”，选择甲旅行社合算；亦有学生认为“包括班主任在内全部按全票的6折优惠”，选择乙旅行社合算。教师引导学生分析、计算，学生得出的方案令我大开眼界，不仅运用了分类讨论思想，还有利用一次函数的解析式、图像与性质考虑的方案，也有利用一元一次不等式、一元一次方程考虑的方案。计算的结果亦出乎学生的意料：要看参加旅游的人数才能确定选择哪一家旅行社更合算。若4名学生参加，则选择两家旅行社价钱一样；少于4名学生参加，选择乙旅行社合算；多于4名学生参加，选择甲旅行社合算。

创设悬念性问题情境，使学生对某种知识产生一种急于想解决问题的心理，能够激起学生强烈的求知欲望。学生可能会给出许多不同的解决方案，产生不同的认知冲突，教师这时应不失时机地引导学生进行小组合作探究，让他们自己发现解决问题的方法，体验成功的快乐。

德国教育家第斯多惠说：“教学的艺术不在于传授的本领，而在于激励、唤醒、鼓舞。”创设有效的数学问题情境，不仅能引发学生的兴趣和思维，激发学生探究的欲望，而且情景交融，让学生置身其中，可以享受到学习数学的乐趣，久而久之，学生便成了数学学习的主人。

[1]中华人民共和国教育部.全日制义务教育数学教育课程标准（实验稿）[M].北京：北京师范大学出版社,2001.

[2]徐杰，王丽丽.数学教学中创设问题情境的认识与实践[J].中学数学教育：初中版，2006（1/2）.

[3]裘桢东.让生活“走进”数学课堂——谈数学课堂教学情境创设的一点体会[J].中学数学教育初中版，2006（1/2）.

[4]赖芍良.精心创设情境，激发学习兴趣，提高课堂效益[J].肇庆教育研究，2011（3）.