超高速撞击中靶后碎片云的内外边界方程研究
2018-07-09贾光辉刘巧霞
贾光辉,刘巧霞,张 榜
(北京航空航天大学 宇航学院,北京 100191)
0 引言
空间碎片超高速撞击严重威胁着低地球轨道航天器的安全。为保障在轨航天器的安全运行,Whipple在1947年提出在航天器舱壁外面一定距离处放置一块防护屏,即Whipple防护,后来又发展了填充式防护或多层防护[1-2]。当空间碎片击穿防护屏,会在防护屏后方形成碎片云,使得空间碎片对航天器舱壁的威胁变成碎片云对舱壁的威胁[3]。因此,研究超高速撞击防护靶形成的碎片云特性对航天器防护结构设计具有重要意义。不同撞击条件下形成的碎片云具有不同的特性[4],根据撞击角度可将碎片云分为斜撞击碎片云和正撞击碎片云,本文针对超高速正撞击形成的碎片云特性进行研究。
在已有的碎片云形状模型中,Swift等[5]首先提出靶后碎片云均匀分布在球壳上的模型,该模型虽结果不甚精确,但建模思想具有开创性;Corvonato等[6]采用伯努利双纽线建立了靶后碎片云的边界方程,使得碎片云形状更贴近实际;迟润强[7]在Corvonato等研究的基础上,保留靶后碎片云的双纽线边界方程,并且利用双曲线方程建立了反溅碎片云的边界方程。然而,以上边界方程模型只建立了碎片云的外边界方程,没有区分靶板和弹丸的内外边界。
本文将碎片云根据材料来源分为靶板碎片云和弹丸碎片云,基于数值仿真结果分别建立这两种碎片云的内外边界方程,进而得到整体碎片云的形状模型,旨在为航天器防护结构设计提供参考。
1 数值仿真的有效性验证
文献[8]给出一组碎片超高速撞击实验案例:直径 0.953cm 铝球(Al 2017.T4)以 6.64 km/s速度垂直撞击厚度 0.22cm 铝板(Al 6061.T6)。案例的实验照片如图1所示,实验所用球/板的材料参数见表1。

图1 撞击发生后 6 μs 及 19.8 μs 的实验碎片云Fig.1 Debris clouds obtained in experiment at 6 μs and 19.8 μs
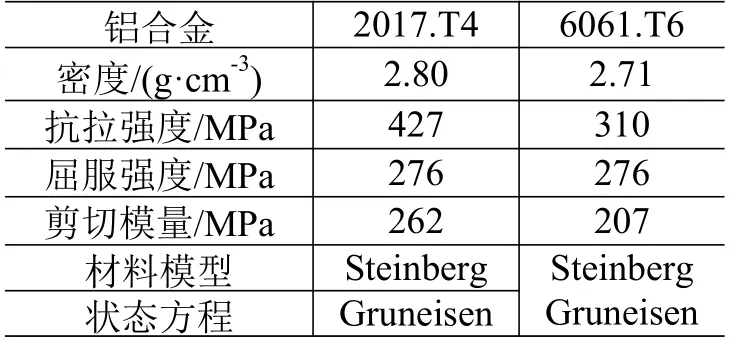
表1 超高速撞击实验所用材料参数Table 1 Material parameters for the hypervelocity impact experiment
采用SPH算法对上述算例的工况建模并进行仿真计算,建模时SPH立方体粒子的边长取0.004 4cm,粒子数为 6 773 984,材料模型的主要参数见表1。仿真结果与实验结果的叠加对比如图2所示,可见数值仿真结果与对应实验结果的一致性很好,说明采用SPH算法是可行的。

图2 撞击发生后 6 μs及 19.8 μs的 SPH 仿真碎片云与实验碎片云对比Fig.2 Comparison of debris clouds obtained in simulation and experiment at 6 μs and 19.8 μs
2 碎片云形状的双纽线边界方程
2.1 双纽线边界方程
2001年,Corvonato等基于碎片云满足自相似性的假设,采用伯努利双纽线作为碎片云形状的边界函数[6],建立了碎片云形状模型。所谓碎片云的自相似性即在演化过程中碎片云的形状始终保持不变。其理论基础为:弹丸与靶板发生撞击后,撞击体的材料迅速破碎,碎片之间没有相互作用力可以用来获取相对加速度,故碎片做匀速直线运动。基于该假设,可将各时刻碎片云粒子的物理坐标(x,y)分别沿着横坐标/纵坐标进行碎片云粒子物理坐标的归一化,得到自然坐标(ξ,η)下的碎片云分布,其变换式为

式中:xmax和ymax分别表示对应时刻碎片云粒子在正x向和正y向的最大值。
在自然坐标下,为使η=φ(ξ)满足伯努利双纽线方程,需要对自然坐标(ξ,η)进一步变换得到新自然坐标 (ξ′,η′),变换式为

Corvonato提出碎片云形状的边界方程满足双纽线函数[6],并将碎片云根据材料来源分为靶板碎片云和弹丸碎片云,其中靶板碎片云的边界为外边界,其边界方程为

弹丸碎片云的边界为内边界,其边界方程为

式中K为内外边界方程的比例系数,可由靶板碎片云最前端速度与弹丸碎片云最前端速度的比值得到,且K关于厚径比和撞击速度的函数关系[6]为
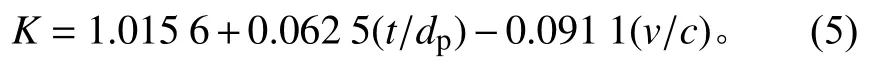
式中:t为铝板厚度,cm;dp为铝球直径,cm;v为撞击速度,km/s;c为材料中的声速,km/s。
若取K=0.8,则碎片云边界如图3所示,图中外边界为靶板碎片云的外边界,内边界既是靶板碎片云的内边界又是弹丸碎片云的外边界。
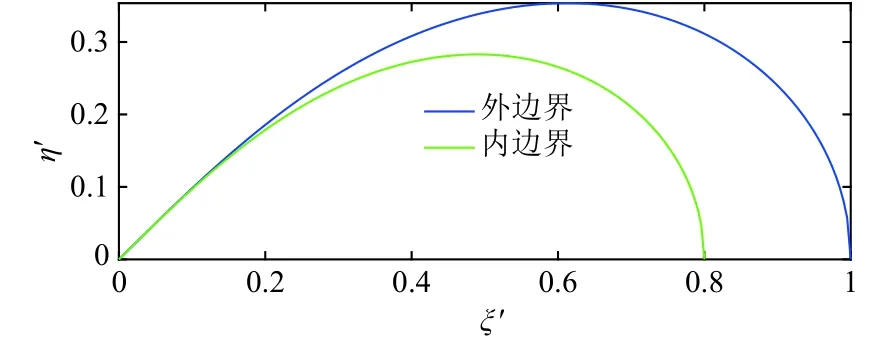
图3 由文献[6]碎片云边界方程得到的碎片云边界Fig.3 Boundary curves of debris cloud for Ref.[6]
2.2 双纽线边界方程的适用性分析
本文针对直径 0.6cm的铝球以5.5~8 km/s的速度垂直撞击厚度0.16cm铝板的工况研究靶后碎片云的内外边界方程,其中算例的工况设置与文献[6]相同,以便对比。
撞击速度为6 km/s的工况下,根据式(5)确定内外边界方程的比例系数K为0.93,根据式(3)、式(4)得到算例靶后碎片云的内外边界方程,整体碎片云、靶板碎片云和弹丸碎片云在新自然坐标系的分布分别如图4、图5和图6所示。
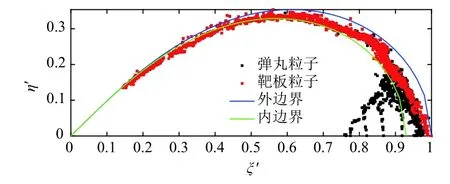
图4 整体碎片云分布Fig.4 Distribution of the entire debris cloud

图5 靶板碎片云分布Fig.5 Distribution of target debris cloud

图6 弹丸碎片云分布Fig.6 Distribution of projectile debris cloud
为了衡量边界方程的适用性,提出边界方程适用率概念。在新自然坐标系下,若碎片云粒子p分布在所给的边界内,说明粒子p满足该边界方程,反之则不满足该边界方程。将满足边界方程的粒子数与碎片云总粒子数的比值称为边界方程适用率,简称适用率。统计图5中分布在内外边界间的靶板粒子数n1,n1与靶板总粒子数n2的比值即为靶板适用率;统计图6中分布在内边界里的弹丸粒子数n3,n3与弹丸总粒子数n4的比值即为弹丸适用率;(n1+n3)与(n2+n4)的比值即为碎片云整体适用率。根据文献[6]所给双纽线边界方程,得到算例对应的双纽线边界方程的靶板、弹丸和整体适用率分别为0.615 2、0.146 4 和0.353,可见其整体适用率较低,说明双纽线边界方程的描述不完善,应根据碎片云的分布特点修正碎片云的内外边界方程。
3 碎片云的内外边界方程修正
3.1 内外边界方程
由图5和图6可看出:对于靶板碎片云部分,头部出现缩颈;对于弹丸碎片云部分,头部明显后凸。因此本文认为碎片云边界方程应用分段函数表示,设分界线为ξ′=m。根据图1,假设碎片云边界的分段函数由双纽线和圆弧曲线组成。在新自然坐标系下,靶板碎片云粒子基本满足等厚度(设厚度符号为tr,量纲为1)的壳体分布,根据分界点将靶板碎片云粒子分为靶板前段和靶板后段2部分,如图7所示。同样,根据分界点将弹丸碎片云粒子分为弹丸前段(包括弹丸碎片云头部后凸部分)和弹丸后段2部分,如图8所示。在新自然坐标系下讨论:1)靶板后段内外边界方程;2)靶板前段内外边界方程;3)弹丸后段内外边界方程;4)弹丸前段内外边界方程。
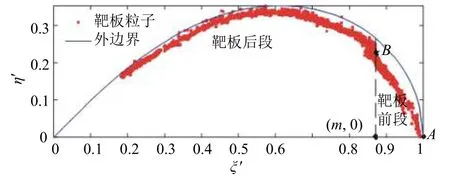
图7 靶板碎片云分布特征Fig.7 Distribution characteristics of target debris cloud

图8 弹丸碎片云分布特征Fig.8 Distribution characteristics of projectile debris cloud
1)靶板后段内外边界方程
根据图7可知靶板后段外边界基本满足双纽线方程

根据靶板碎片云等厚度tr壳体分布,可确定靶板后段内边界双纽线方程。具体方法如下:
首先,靶板后段内边界曲线满足双纽线

式中:(ξ0′,η0′)为双纽线的顶点;a为双纽线系数,a>0。
由靶后碎片云关于ξ′轴对称,得η0′=0;靶板碎片云等厚度tr壳体分布,因此由式(6)可知靶板内边界函数在顶点处的法线方向与ξ′轴的夹角为45°,故得靶板碎片云内边界函数过顶点和端点(1−tr,0),代入式(7)可得到靶板后段内边界的双纽线方程,其中。
2)靶板前段内外边界方程
利用三点定圆原理确定靶板前段内外边界方程。如图7 所示:由A(1,0)、B(m,φ(m)−tr)、B′(m,-[φ(m)−tr])三点可确定靶板前段外边界圆弧方程(点B′是点B的ξ′轴对称点);由于靶板前段碎片云等厚度tr壳体分布,其内外边界是同心圆,所以可由靶板前段外边界圆弧方程和壳体厚度tr直接确定靶板前段内边界圆弧方程。
3)弹丸后段内外边界方程
根据图7和图8的对比可知,弹丸后段和靶板后段分布区域基本重合,故弹丸后段与靶板后段有相同的内外边界方程。
4)弹丸前段内外边界方程
为了得到弹丸前段内外边界条件,取弹丸前段在ξ′方向的特征点D(n,0)和C(k,0),利用三点定圆原理确定弹丸前段内外边界方程。如图8所示,由C(k,0)、B(m,φ(m)−tr)、B′(m,-[φ(m)−tr])三点可确定弹丸前段外边界圆弧方程;由D(n,0)、E(m−tr,φ(m)−tr)、E′(m−tr,-[φ(m)−tr])三点可确定弹丸前段内边界圆弧方程(点E′是点E的ξ′轴对称点)。
双纽线与圆弧在分界ξ′=m处不是连续函数,因此在分界处将靶板后段外边界双纽线对应边界点与靶板前段外边界圆弧对应边界点用直线连接,并用同样的方法处理靶板前后内边界、弹丸前后外边界、弹丸前后内边界。图5、图6对应算例的特征参数为:tr=0.04,m=0.886,n=0.76,k=0.98。
为研究撞击速度对边界方程的影响,本文开展了直径为0.6cm的铝球以5.5~8.0 km/s的速度垂直撞击厚度0.16cm铝板的数值仿真,工况见表2。根据仿真结果,用同样的处理方法,统计各算例的4 个特征参数(tr、m、n、k),见表2。
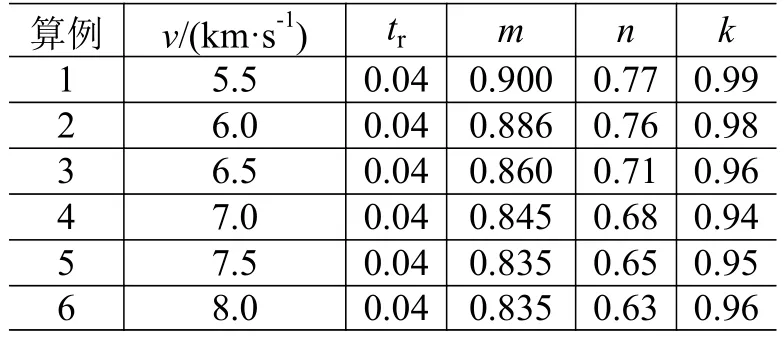
表2 各算例的 4 个特征参数Table 2 Determination of parameters
进一步分析撞击速度对4个特征参数的影响:参数tr为常数,tr=0.04;参数k随速度的变化较小,且接近于1;参数m随撞击速度增加而减小,即分界点后移,

参数n相对于其他3个参数变化幅度最大,其值随撞击速度增加而减小,即弹丸碎片云后端点后移,

根据m、n值的变化可知,在撞击速度v=5.5~8.0 km/s的范围内,撞击速度越大,撞击材料的破碎程度越高,使得m、n值越小。
3.2 修正后内外边界方程的具体形式
以表2中算例2为例, 4个特征参数为:tr=0.04、m=0.886、n=0.76、k=0.98,其碎片云的边界方程见式(6)和式(10)~(13)。
1)靶板后段内外边界方程
靶板后段外边界方程为式(6)。
靶板后段内边界方程为

2)靶板前段内外边界方程
靶板前段外边界方程为

靶板前段内边界方程为
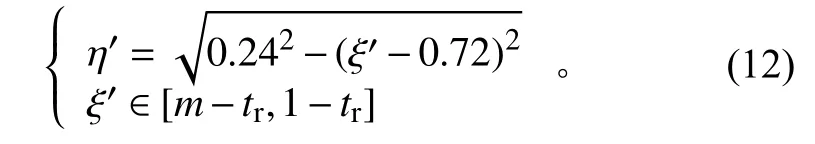
3)弹丸后段内外边界方程
弹丸后段外边界方程与靶板后段外边界方程一致,为式(6)。弹丸后段内边界方程与靶板后段内边界方程一致,为式(10)。
4)弹丸前段内外边界方程
弹丸前段外边界方程与靶板前段外边界方程一致,为式(11)。
弹丸前段内边界方程为

根据式(6)和式(10)~(13),靶板碎片云边界和弹丸碎片云边界分别如图9和图10所示。
在新自然坐标下,根据双纽线方程和圆弧方程组成的边界方程,可得算例2的适用率,与双纽线边界方程的适用率进行对比(见表3)可知:靶板适用率由61.52%提高到95.07%;弹丸适用率由14.64%提高到97.22%,碎片云整体适用率由35.3%提高到96.27%。表4是各算例的两种边界方程碎片云整体适用率的对比结果。
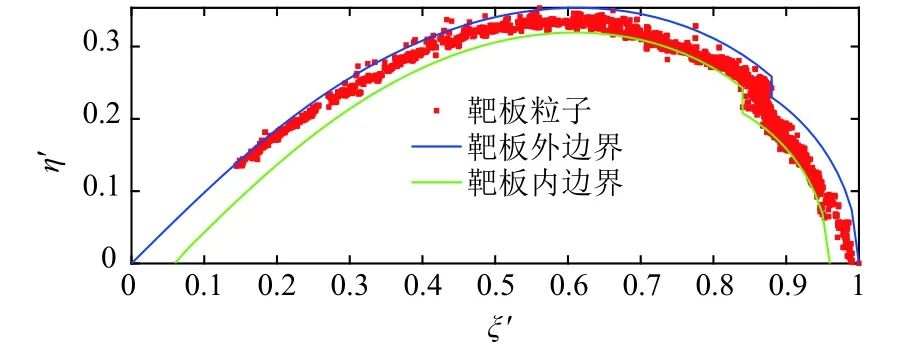
图9 靶板碎片云内外边界Fig.9 The inner and outer boundaries of target debris cloud
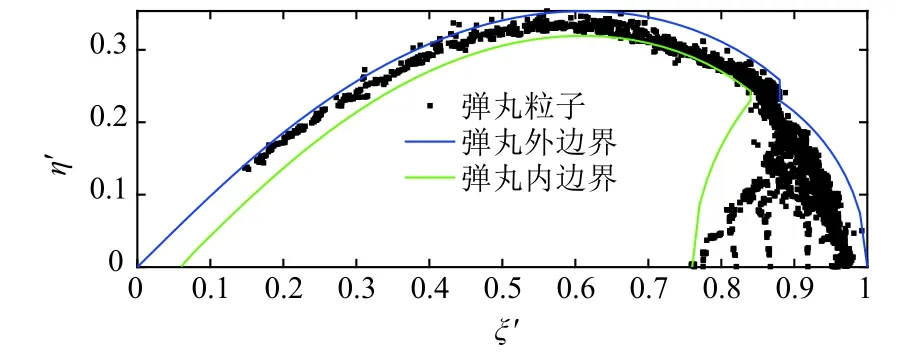
图10 弹丸碎片云内外边界Fig.10 The inner and outer boundaries of projectile debris cloud

表3 算例 2 两种边界方程适用率对比Table 3 Comparison of applicability rate for Example II

表4 各算例的两种边界方程碎片云整体适用率对比Table 4 Comparison of applicability rate for various Examples
最小撞击速度(算例 1:v=5.5 km/s)和最大撞击速度(算例 6:v=8.0 km/s)工况下碎片云的内外边界分布分别如图11和图12所示,可以看出由双纽线方程和圆弧方程组成的边界方程比单一的双纽线边界方程与碎片云实际分布情况更贴合。

图11 算例 1(v=5.5 km/s、t/dp=0.267)碎片云的内外边界分布Fig.11 The inner and outer boundaries of debris cloud in Example I (v=5.5 km/s,t/dp =0.267)

图12 算例 6(v=8.0 km/s、t/dp=0.267)碎片云的内外边界分布Fig.12 The inner and outer boundaries of debris cloud in Example VI (v=8 km/s,t/dp=0.267)
4 结束语
本文采用SPH算法,选取文献[6]中的算例,对直径0.6cm的铝球以5.5~8.0 km/s的速度正撞击厚度0.16cm的铝板进行了仿真计算,研究了碎片云的内外边界方程。
通过分析靶板碎片云、弹丸碎片云以及整体碎片云的适用率,发现单一的双纽线边界方程与碎片云实际分布情况的贴合度不够;基于靶后碎片云的几何分布特点,分别建立靶板碎片云和弹丸碎片云内外边界方程的分段函数(后段仍然采用双纽线方程,前段采用圆弧方程),完整表述了靶后碎片云弹丸内凸、靶板内凹的形状特点;将修正后的由双纽线方程和圆弧方程组成的边界方程与原来单一的双纽线边界方程的整体碎片云适用率进行对比,发现前者与碎片云实际分布情况的贴合度更好。
本文仅探讨了直径为0.6cm的铝球正撞击厚度0.16cm铝板的工况,修正后边界方程在弹靶尺寸方面的普适性有待进一步研究。
[1]贾光辉,姚光乐,张帅.填充式防护结构弹道极限方程的差异演化优化[J/OL].北京航空航天大学学报(2017-11-28)[2018-01-26].http://onlinelibrary.wiley.com/doi/10.13700/j.bh.1001-5965.2017.0515 JIA G H,YAO G L,ZHANG S.Differential evolution optimization for Stuffed Whipple shield ballistic limit equations[J/OL].Journal of Beijing University of Aeronautics and Astronautics (2017-11-28)[2018-01-26].http://onlinelibrary.wiley.com/doi/10.13700/j.bh.1001-5965.2017.0515
[2]CHRISTIANSEN E L.Design and performance equations for advanced meteoroid and debris shields[J].International Journal of Impact Engineering,1993,14(1):145-156
[3]贾光辉,黄海,胡震东,等.空间碎片超高速撞击极限穿透比动能研究[J].宇航学报,2006,27(5):1000-1003 JIA G H,HUANG H,HU Z D,et al.Research on debris kinetic energy per unit area in hypervelocity impacting[J].Journal of Astronautics,2006,27(5):1000-1003
[4]唐蜜,柏劲松,李平,等.超高速撞击中影响碎片云形状因素分析[J].高压物理学报,2007,21(4):425-432 TANG M,BAI J S,LI P,et al.Factors analysis of debris cloud ’s shape of hypervelocity impact[J].Chinese Journal of High Pressure Physics,2007,21(4):425-432
[5]SWIFT H F,BAMFORD R,CHEN R.Designing space vehicle shields for meteoroid protection:a new analysis[J].Advances in Space Research,1982,2(12):219-234
[6]CORVONATO E,DESTEFANIS R,FARAUD M.Integral model for the description of the debris cloud structure and impact[J].International Journal of Impact Engineering,2001,26(1):115-128
[7]迟润强.弹丸超高速撞击薄板碎片云建模研究[D].哈尔滨:哈尔滨工业大学,2010:104-106
[8]LACERDA D,LACOME J-L.Simulations of hypervelocity impacts with smoothed particle hydrodynamics:DYNALIS Report[R].Paris,France,2003
