可降低气动热效应的类凹腔外形优化设计

刘芙群，李 波，孙晓峰，张 亮

（1.中国运载火箭技术研究院，北京 100076； 2.陆军航空兵研究所，北京 101121；3.中国航天空气动力技术研究院，北京 100074）

0 引言

局部防热设计是飞行器研制中的重要问题之一，而局部区域的热环境分析则是局部防热设计的先提条件。由于结构设计偏差以及不同材料间的热膨胀系数不同，飞行器上会呈现出舱段对接螺栓安装槽，操作口盖缝隙，防热结构预留缝隙，防热结构烧蚀不同步引起的前后向台阶和沟槽等常见外形结构。这些空腔和缝隙的存在会对飞行器表面流场产生不同程度的干扰，导致局部区域热流密度和压力的变化，对结构在飞行剖面的可靠性造成隐患。因此开展这类局部结构的热环境预测和防热设计是十分必要的[1-2]。

针对凹腔和缝隙内的热流分布情况，国外很早就开展了大量的研究。1956年，Chapman[3]首次对高超声速流中的缝隙热流分布进行了机理分析，并提出了凹腔内平均热流的计算方法。Burggraf[4]采用近似线性方法求解方腔流动控制方程，得到了空腔内部归一化的热流分布计算关系式。Ben-Yakar等[5]对超声速流中的二维凹腔（D=3mm，L/D=3,5,7）流动进行了实验研究，发现当长深比改变时，凹腔附近的激波结构出现了显著变化；对于较大长深比的凹腔，前缘激波消失并逐渐形成膨胀波。Nestler等[6]对不同长深比的凹腔内的压力和热流分布开展了试验研究，得出了不同长深比凹腔前壁面、后壁面和底部的传热系数规律。

国内也开展了对缝隙热流的部分研究。童秉纲院士[7]根据航天飞机防热瓦缝隙内气体流动的特点，给出了缝隙中的热流与压力、压力梯度和缝隙宽度之间的关系，以及气体流动的特性规律。唐功跃等[2]研究了不同来流条件下的缝隙流场结构，通过简化建立了缝隙内气体的传热模型和热环境计算模型。龚红明等[8]对湍流条件下防热瓦缝隙热环境特性开展了实验研究，结果表明，缝口边缘特别是T字口迎风壁存在很高的局部热流，测量峰值达到11.6倍平板值。房田文等[9]开展了凹腔超声速流场结构的试验研究，分析了不同的长深比和后壁斜角对凹腔内流场的影响。贾真等[10]研究了凹腔前缘角对超声速燃烧室性能的影响，结果表明凹腔前缘角不会实质性地改变流场内波系结构，但减小凹腔前缘角将减弱前缘分离激波强度，较明显增强后壁面再附激波强度。从以上分析不难看出，国内关于缝隙和凹腔的研究主要集中于对缝隙的研究，对凹腔的研究则集中在规则凹腔外形以及凹腔对超声速燃烧室的影响。而飞行器研制中，常常出现各种不规则的类凹腔外形，这些外形的气动加热环境预示和防热设计少有人研究，但此类研究对于飞行器的可靠飞行是必不可少的。

本文采用有限体积法离散差分形式的N-S方程，对飞行器上由凸起物形成的类凹腔气动加热环境进行数值计算，对流场结构和流动机理进行分析，针对凹腔前壁面热流密度过高的问题，提出并验证了降低前壁面前缘热流密度的优化类凹腔外形。

1 凹腔分类

通常以凹腔宽L和深度H的比值L/H对凹腔进行分类，具体标准为：当L/H≤1时为缝隙；当L/H＞1时为凹腔。凹腔又可具体分为开放式凹腔（1＜L/H≤10）、过渡式凹腔（10＜L/H≤14）和封闭式凹腔（L/H＞14），参见图1。本文研究的类凹腔外形不属于任何一种标准凹腔，其前壁面倾斜，后壁面下部垂直、上部倾斜，其结构示意参见图1(f)。

图1 凹腔分类Fig.1 Types of cavities

2 计算模型

为了分析类凹腔外形气动热的三维效应，计算时考虑了飞行器的三维外形。飞行器为双锥+柱外形（见图2），类凹腔外形位于飞行器后部柱段上。类凹腔前壁面为垂直壁面，高3mm；后壁面为复杂外形，最低处为垂直壁面，高8mm，8mm以上为后掠13°、深24mm的斜坡；后壁面和前壁面之间的最小宽度为22mm，形成了一个局部的复杂类凹腔结构，后文简称外形1（见图3(a)）。为了减小外形1中前缘（抗烧蚀性能差的防热材料）处的热流，对其进行外形优化，将前壁面沿轴线方向做45°的倒角，即前缘角由 90°变为 45°，称为外形 2（见图3(b)）。

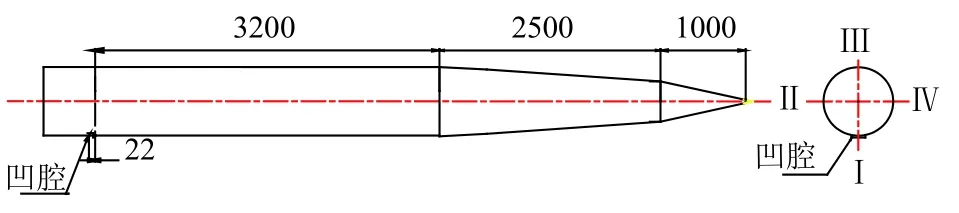
图2 飞行器外形示意Fig.2 Sketch of flight vehicle

图3 类凹腔外形示意Fig.3 Sketch of cavity-like structure

3 数值计算方法

控制方程为三维非定常可压缩N-S方程，采用有限体积法进行离散，具体形式可参见文献[11]。空间离散格式对于流场的计算精度和稳定性均有较大影响，本文采用ROE的FDS格式进行界面无黏数值通量的计算。计算过程中人为引入熵修正，将非物理的膨胀激波耗散为膨胀扇区，使之满足熵条件，采用Spalart-Allmaras方程湍流模型[11]对湍流影响进行模拟。

热环境的数值模拟依赖于壁面处温度边界层的刻画，因此近壁面的网格质量对热环境的模拟结果起到决定作用[12]。为保证近壁面网格的光滑性和正交性，近壁区采用O型网格拓扑结构，壁面第一层网格法向尺度为10-3mm。

4 数值方法验证

选择飞行器标模外形对数值算法进行验证。来流条件为：马赫数Ma=8.0，攻角α=0°，单位雷诺数Re=7.0×106/m，温度Te=88.5 K，湍流状态；壁温Tw=288 K。图4给出了标模外形的CFD计算网格（图4(a)）及计算结果与试验结果的比较（图4(b)），可以看到，CFD计算结果均与实验数据吻合较好，验证了本文采用CFD方法的可靠性。

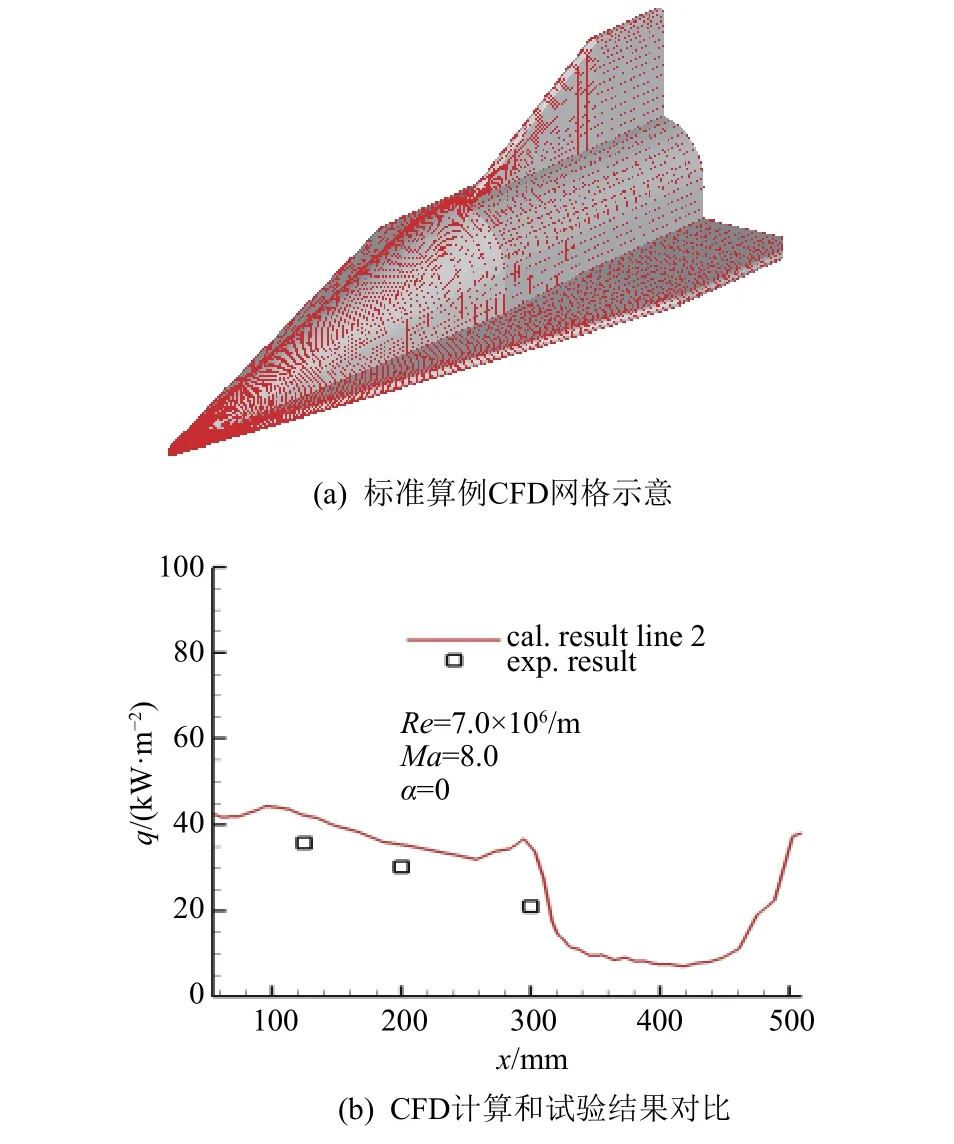
图4 CFD 数值方法验证Fig.4 Validation of the numerical model

5 计算结果与分析

采用与标模计算相似的网格划分方式和数值计算方法，对本文研究的2个类凹腔外形进行数值计算。计算的来流条件为：马赫数Ma=6.14，攻角α=0°，单位雷诺数Re=9.2×106/m，温度Te=217.9 K，湍流状态；壁面温度Tw=273 K。计算结果分析如下。

5.1 流场分析

采用上述CFD方法进行流场分析，给出了类凹腔外形优化前后对称面上的流线分布（图5）。从图5(a)可以看出，外形1（优化前）的流场结构具有以下特点：

1）整体流场结构接近于封闭式凹腔的流场结构形式。

2）气流在前缘处分离膨胀形成一个低压区，靠近前壁面底部原来静止的气体向该低压区流动，流到分离角处时又受到分离流的剪切作用而向下游流动，在分离角的底部形成一个小的旋涡，即图中的副涡1。

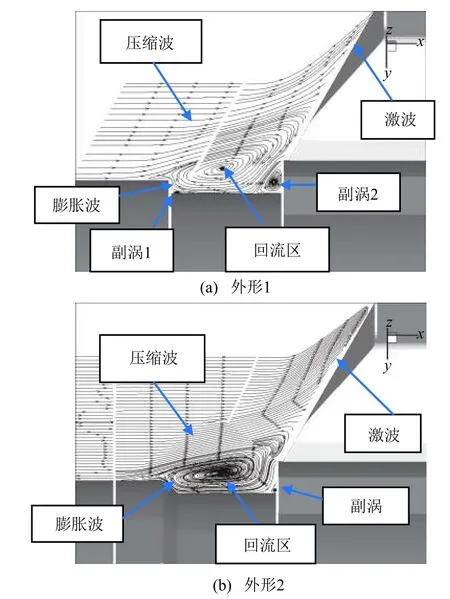
图5 类凹腔外形优化前后的流场结构图Fig.5 Flow field structure of cavity-like structure before/after optimization

3）在后壁面处由于气流被压缩分离，在后缘处形成一个高压区，该高压区中的气体向其下游的静压区流动，然后受到主涡旋的作用又向上游逆向流动，当流到再附区时又受到再压缩气体的剪切作用而向下游流动，在后壁面的分离角底部形成另一个小的旋涡，即图中的副涡2。

4）前后壁面的高度不同，因此形成的副涡大小不同，前壁面较低，分离膨胀较弱，分离涡较小；后壁面高度较高，气流强烈压缩，因此其分离距离和高压区范围均较大，形成的分离涡大于前壁面产生的。

5）凹腔后壁面高度较高，回流区尺寸较大，对来流产生了压缩效应；在压缩波的作用下，来流气体向壁面外侧方向偏转。

从图5(b)可以看出，外形2（优化后）的流场结构具有以下特点：

1）与外形1的流场涡旋主结构相似，但是外形的变化带来了副涡流动结构强度和大小的变化。

2）前壁面3mm高的垂直壁面变为45°的斜面，使得前缘角变小，导致主要源于前缘而形成的膨胀减弱，所形成的类似外形1中副涡1的旋涡不明显。

3）前缘角变小还导致凹腔底部的尺寸由20mm缩短为18.5mm，使凹腔内更容易形成大涡，来流更容易被卷吸入凹腔内部，而后壁面形成的激波引起边界层分离形成较小的回流区。

4）外形优化对于流场有显著的调节作用，最终实现了前壁面热流密度的降低。

5.2 热流分析

图6给出了类凹腔外形优化前后的热流分布。

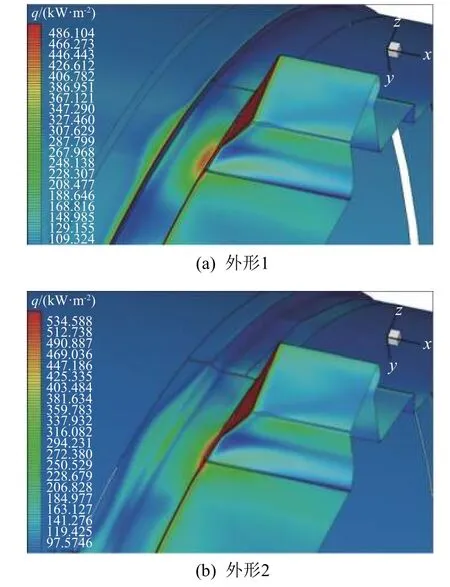
图6 凹腔外形优化前后的热流密度分布Fig.6 Heat flux contour before/after optimization

从图6(a)可以看出：

1）外形1的凹腔底部由于气流分离再附，形成了局部的热流极值，出现在副涡2处，距离后壁面约5mm，该热流极值最高可为当地未干扰热流的3～5倍；后壁面前干扰区的大部分区域热流值为当地未干扰热流的2～3倍，干扰范围较小。

2）外形1靠近前壁面的凹腔底部干扰热流也较为明显，大约为当地无干扰热流的2倍。

3）外形1凹腔前缘处最大热流峰值可达当地未干扰热流的8～10倍。

从图6(b)可以看出：

1）外形2的凹腔底部热流分布与外形1的类似，在副涡2处出现了局部的热流极值，距离后壁面约3mm，该热流极值略高于外形1的，但高热流区域小于外形1的。这和文献[10]的结论一致。

2）外形2前壁面的干扰区范围增大，整个斜坡前壁面均为干扰区，热流值小于外形1的。

3）外形2的凹腔前缘热流明显降低，最高热流为当地无干扰热流的1.5～2倍，外形优化效果明显。

6 结论

本文对飞行器上由凸起物形成的类凹腔外形进行了优化设计和数值仿真验证，对优化前后的流场结构进行了分析，对流动机理进行了研究，结果表明：

1）本文使用的数值计算方法可用于凹腔的气动热计算和分析；

2）优化前的凹腔流场结构类似于封闭式凹腔的结构，壁面高度影响分离涡的大小；

3）优化后的凹腔流场结构类似于前壁倾斜式凹腔，前壁面未形成明显的分离涡；

4）凹腔前缘角的减小降低了前缘的气动加热热流密度（下降至优化前的20%），对凹腔底部以及后壁面的热流密度影响不大，达到了外形优化设计的目的。

[1]李素循.激波与边界层主导的复杂流动[M].北京:科学出版社,2007:4-11

[2]唐功跃,吴国庭,姜贵庆.缝隙流动分析及其热环境的工程计算[J].中国空间科学技术,1996,16(6):1-7

[3]CHAPMAN D R A.Theoretical analysis of heat transfer in regions of separated flow:NACA-TN 3792[R],1956

[4]BURGGRAF O R.A model of steady separated flow in rectangular caviies at high Reynolds number[C]//Proceedings of the 1965 Heat Transfer and Fluid Mechanics Institute.Palo Alto:Stanford University Press,1965:190-229

[5]BENYAKAR A,HANSON R K.Supersonic combustion of cross flow jets and the influence of cavity flame holders:AIAA-99-0484 [R],1999

[6]NESTLER D E,SAYDAH A R,AUXER W L.Heat transfer to steps and cavities in hypersonic turbulent flow[C]//AIAA Fluid and Plasma Dynamics Conference.Los Angeles,California,1968

[7]童秉纲.航天飞机防热瓦缝隙气动加热的讨论[J].气动试验与测量控制,1999,4(4):1-8 TONG B G.A qualitative study of the gap heating on space shuttle[J].Aerodynamic Experiment and Measurement & Control,1999,4(4):1-8

[8]龚红明,陈景秋,李理.湍流条件下防热瓦缝隙热环境特性实验研究[J].实验流体力学,2015,29(2):13-18 GONG H M,CHEN J Q,LI L.Experimental investigation on the aerodynamic heating to tile-to-tile gaps in turbulent boundary layer[J].Journal of Experiments in Fluid Mechananics,2015,29(2):13-18

[9]房田文,丁猛,周进.凹腔超声速流场结构的试验研究[J].国防科技大学学报,2007,29(3):1-5 FANG T W,DING M,ZHOU J.Experimental investigation on supersonic flows over cavities[J].Journal of National University of Defense Technology,2007,29(3):1-5

[10]贾真,吴迪,朴英,等.凹腔前缘角对超声速燃烧室性能的影响[J].航空动力学报,2012,27(5):993-998 JIA Z,WU D,PIAO Y,et al.Effect of cabity leading edge angle on performance of supersonic combustor[J].Journal of Aerospace Power,2012,27(5):993-998

[11]阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2007:27-28

[12]阎超,禹建军,李君哲.热流 CFD 计算中格式和网格效应若干问题 研究[J].空气动力学学报,2006,24(1):125-130 YAN C,YU J J,LI J Z.Scheme effect and grid dependency in CFD computations of heat trans[J].Acta Aerodynamica Sinica,2006,24(1):125-130