基于外在扰动的双寡头价格博弈模型分析

白雪寒,徐玉华,杜明娟(南京审计大学金融学院, 江苏 南京 211815)

寡头竞争是市场竞争的重要形式，价格竞争也是目前营销活动中经常选择的策略。Cournot模型是博弈论中经典的同质产品以产量竞争的模型，伯川德(Bertrand)[1]认为日常情况下企业更偏向于运用价格竞争的策略。然而，伯川德模型中价格决策机制会造成均衡价格和边际成本相等的利润为零的状况，这就是所谓的“伯川德悖论”。豪泰林(Hotelling)[2]之后合理地解开了这一悖论，他表明有差异的商品之间的替代弹性变小，因此消费者对有差异商品的偏好不同，此时均衡价格也就可以大于边际成本。Agliari[3]在不断的调整策略中证实了产品的差异性越大，纳什均衡越不稳定；杨晓花等[4]侧重研究了行动时机和策略变量类型即选择价格还是产量竞争的双重内生选择下双寡头博弈的均衡；Frisch[5]提出了推测变差模型,因为推测变差的不同，所以产生的推测变差均衡也不同；Kopel等[6]的研究把双寡头推向多寡头。实现古诺均衡、伯川德均衡的前提条件是竞争参与者可以获得市场的完全信息并且是完全理性的决策，在现实生活中该类条件很难满足。Agiza和Elsadany[7]对古诺模型进行了改进，有限理性、天真理性和适应性假设等混合理性假设被嵌入到模型中，并证明了均衡点的存在性；董文波等[8]在有限理性的基础上构建了具有溢出效应的双寡头价格博弈模型；赵德余等[9]将市场价格竞争、产品差异化定位策略以及相关的消费者需求分布和边际成本优势等被孤立的问题综合考虑进行研究；郭军华等[10]将研究深入到了外部因素的政府补贴，得出适当的政府补贴机制可促使博弈系统演化至制造商均选择进入再制造策略的均衡。

现实中的寡头企业在决策中不仅受自身条件的限制也受到外部因素的影响，如政府的重大决策、经济危机等。文献[1～10]对寡头博弈做了很多有价值的探讨，然而关于外部扰动项对寡头决策的影响的文献并不多。下面，笔者基于决策过程中的扰动项建立决策模型，分析了扰动后的经济系统混沌行为，旨在为企业提供适时调整竞争决策的科学依据。

1 博弈模型

假设企业1和企业2为国内某一产业的2家寡头企业且分别为领导者和追随者角色，即企业2倾向于模仿企业1的决策行为，2家企业的需求函数为：

qi(pi,pj)=ai-dipi+bipji,j=1,2且i≠j

(1)

其中，ai,di>0,0≤bi≤1；ai为公司1和公司2的潜在需求量；p1，p2分别表示公司1和公司2的产品价格；bi代表2种商品的替代性，bi越大商品的替代性越强，bi=1时2种商品具有完全替代性。

假设2个企业的二次成本函数为：

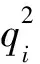
(2)

其中，ci>0，即认为随着产量达到了一定的程度，由于人工和原材料的供应的紧张而造成生产成本快速上涨。

在博弈的市场结构下，2家企业的利润函数为:

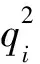
(3)

计算式(3)的边际利润函数可得：

(4)

设Ai=ai(1+2cidi)，Bi=2di(1+cidi)，Di=bi(1+2cidi)， 则式(4)变为：

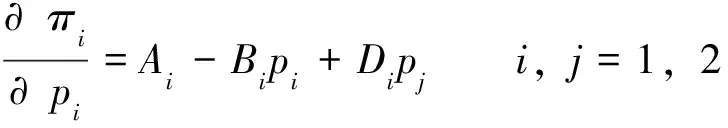
(5)

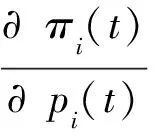
(6)

(7)

将式(5)代入式(6)和式(7)，得到如下动态博弈系统公式：

p1(t+1)=p1(t)+α1p1(t)[A1-B1p1(t)+D1p2(t)]+αp1(t)

(8)

p2(t+1)=p2(t)+α2p2(t)[A2-B2p2(t)+D2p1(t)]

(9)

式(8)和式(9)的4个均衡解为：

可以看出，均衡解中α2没有出现，说明α1和α间接地影响企业2达到决策均衡状态。

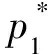
2 局部稳定性分析

为了分析以上平衡点的稳定性，获得动态系统的雅可比矩阵如下：

(10)

根据均衡点的特征可知E0、E1、E2均为边界均衡点，其中,E0为不稳定点，E1、E2为鞍点，E3是唯一的纳什均衡点。E3的雅可比矩阵为：

(11)

J3的特征多项式为：

f(λ)=λ2-Tr(J3)λ+Det(J3)

式中， Tr(J3)为雅可比矩阵J3的迹；Det(J3)为雅可比矩阵J3的行列式。

又：

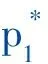
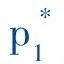
这说明纳什均衡的特征值是实的。下面给出纳什均衡E3的充分必要条件。纳什均衡的局部稳定性可以由Jury条件给出，即：

(12)

在式(12)中，确定除参数α1，α2，α外其他参数后，满足不等式(12)的全体(α1，α2，α)的值即为纳什均衡点E3稳定区域。如果(α1，α2，α)在稳定域中，则在经历一系列轮次的博弈后，(p1(t),p2(t))稳定于E3，如果(α1,α2,α)不在稳定域中，经过多次博弈之后，系统会逐渐失去稳定。

3 数值模拟分析

笔者借助Matlab进行数值仿真，取a1=a2=3.5，b1=b2=0.25，c1=c2=0.5，d1=d2=1,α1=0.23。因为α是干扰项系数，所以在仿真中对其取不同的值来进行对比。

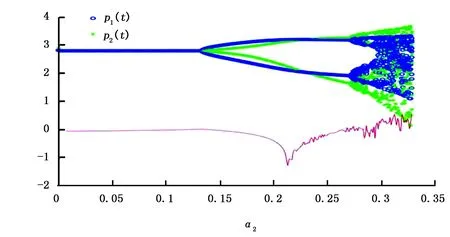
图1 价格分叉和Lyapunov指数图(α=0)

图1～图5是α=0、0.01、0.1、-0.03、-0.1时的价格分叉和Lyapunov指数图，在分叉图中可以看出α对企业1的影响以及间接对企业2的影响。由图1可以看出，当假设扰动项不存在时，在固定α1的条件下，第1次价格分叉在Lyapunov指数图中对应α2=0.1320，第2次分叉对应α2=0.2763。从双寡头价格博弈模型的演化路径可以看出，随着α2的取值变化，价格模型呈现出倍周期分叉并最终处于混沌状态。寡头双方价格的混沌状态对企业的经营十分不利，价格的过大波动会导致企业无法制定合理有效的生产计划。

当α=0.01时，价格博弈演化中的第1次和第2次分叉在Lyapunov指数图中分别对应α2=0.1286和0.2694(见图2)。此时α取正数意味着外界有利的扰动促使企业提高商品价格，当企业因为得到外部利好消息提高商品价格时，从演化路径中可以看出分叉和进入混沌状态的点均比不考虑扰动时提前。

当扰动项系数α=0.1时，领导者企业1的价格分叉更早提前，随着企业2对企业1的追随模仿，不久企业2的价格也出现分叉，经过一段时间2家企业在对应几乎相同的Lyapunov指数图中的点处再次分叉进入混沌状态(见图3)。因此，当外部出现利好因素企业不可盲目大幅提高商品价格，应权衡多种因素做出决策。

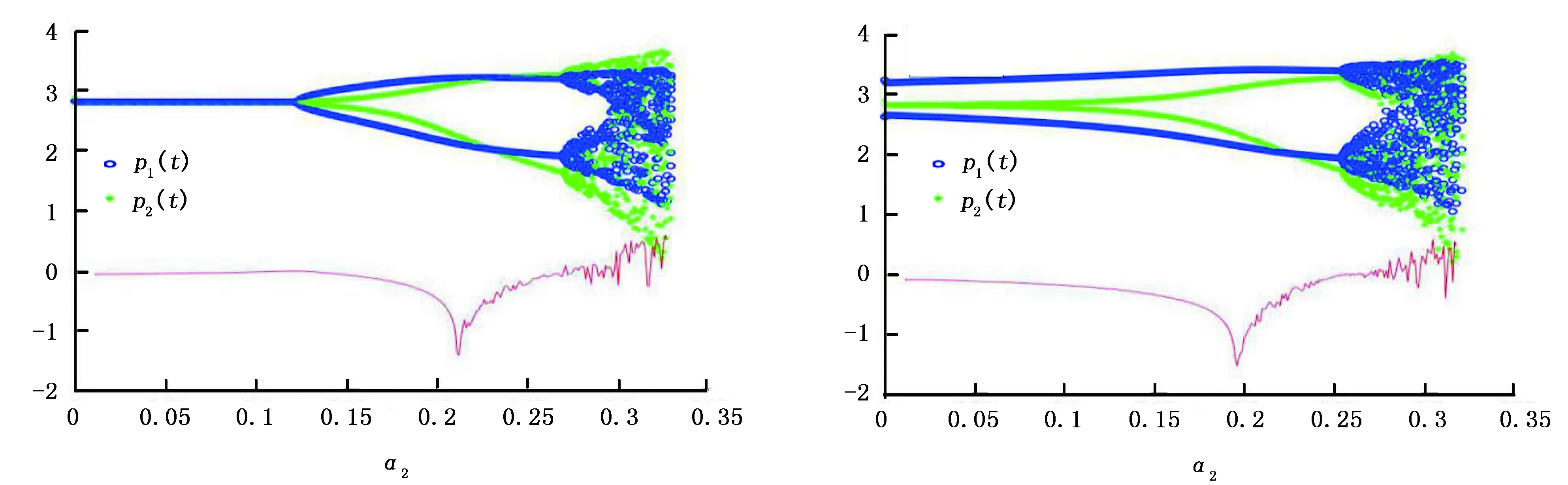
图2 价格分叉和Lyapunov指数图(α=0.01) 图3 价格分叉和Lyapunov指数图(α=0.1)

当α=-0.03时，由图4可以看出第1个分叉点α2=0.1521和第2个分叉点α2=0.2815相比于图1的分叉点均有推迟。α小于零意味着外部出现不利因素的扰动，企业对商品进行降价，此时对价格的微调便可推迟价格博弈系统的分叉和混沌。

当α=-0.1时，由图5可以看出第1个分叉点α1=0.2513和第2个分叉点α2=0.3258相比于图4的分叉点有进一步的推迟，这说明企业依据外部不利扰动的程度在竞争决策中对商品降价有利于维持系统的稳定。但是当取负数的α过小将失去研究的意义。

从以上分叉图中可以看出，α不同的取值对2个企业在采取价格决策竞争中的影响十分显著，企业在决策中应充分考虑外界扰动因素，并采取适当措施来稳定经营状态。

图4 价格分叉和Lyapunov指数图(α=-0.03) 图5 价格分叉和Lyapunov指数图(α=-0.1)

4 结论

在假设2个寡头企业分别为领导者和追随者的角色且具有有限理性的前提下，基于差异化产品的寡头模型，并结合扰动项构建价格竞争模型的动态系统研究外界干扰因素下该模型的稳定性和分叉行为的演化，得出如下结论：

1)外在扰动会加剧价格决策系统的不稳定性；

2)当存在有利的外部因素时，企业在有限理性下会在价格决策机制中使扰动项系数为正即提高商品价格，此时扰动项系数微小的变化即可造成竞争中价格决策系统分叉的提前，当扰动项系数大到一定程度极有可能使系统直接进入混沌状态；

3)当外界扰动因素产生负影响时，结合心理学来分析，基于有限理性的寡头企业并不愿意在下期价格决策中降低价格，通过分叉图可以看出此时稍微降低价格反而会增加系统的稳定，推迟价格决策系统的分叉及混沌现象，因此，企业在竞争决策中应考虑外部扰动因素，审慎行动。

[参考文献]

[1]Bertrand J. Theorie mathematique de la richesse societe. Journal des Savants[J]. Journals des Savants, 1883: 498～501.

[2]Hotelling H. Stability in competition [J]. The Economic Journal, 1929, 39: 52～56.

[3]Agliasi A, Naimzada A K, Pecora N. Nonlinear dynamics of a Cournot duopoly game with differ-entiated products[J]. Applied Mathematics and Computation, 2016, 281: 1～8.

[4]杨晓花，夏火松，杨云峰.双重内生选择下双寡头博弈的均衡研究[J].中国管理科学，2010(3):141～147.

[5]Frisch R.Monopoly，Polypoly:The Concept of Force in the Economy[J].International E-conomic Papers,1951, 1：22～27.

[6]Kopel M.Simple and Complex Adjustment Dynamics in the Cournot Duopoly Models[J].Chaos，Solitons and Fractals, 1996,7：2031～2036.

[7]Agiza H N，Elsadany A. A,Nonlinear Dynamics in the Cournot Duopoly Game with Heterogeneous Players[J].Physica A, 2003，320：512～516.

[8]董文波，范明，杜建国.有限理性双寡头价格博弈模型的混沌分析[J].决策参考，2014(5):35～39.

[9]赵德余，顾海英，刘晨.双寡头垄断市场的价格竞争与产品差异化策略[J].管理科学学报，2006(5)：1～7.

[10]郭军华，李帮义，倪明.双寡头再制造进入决策的演化博弈分析[J].系统工程理论与实践，2013(2)：370～377.