Wolfe线搜索下的一个修正DY谱共轭梯度法

房明磊，孙敏(安徽理工大学数学与大数据学院，安徽 淮南 232001)

1 共轭梯度法

考虑如下无约束非线性优化问题：

min{f(x)}|x∈Rn}

(1)

式中，x是决策变量；目标函数f:Rn→R是一光滑的非线性函数。

共轭梯度法是解决上述大规模非线性优化问题的比较有效的常用方法，有着低存储、易计算的优点，其迭代格式的一般形式为：

xk+1=xk+αkdk

(2)

(3)

式中，gk=f(xk)是f(x)在点xk处的梯度；αk是满足某种线搜索的步长；βk是标量，是调控方向的参数。

不同的βk选取方式对应着不同的共轭梯度法，著名的βk的计算公式[1～7]有：

其中， ‖·‖表示范数。

以上6个公式所对应的算法中， PRP、HS和LS方法具有很好的实验效果，FR、DY和CD方法具有较强的收敛性质。为了利用共轭梯度法各自的特点，许多学者在这些公式的基础上进行了大量的研究，对经典的βk公式进行修改，有的是着重非负性改进，有的是着眼于充分下降性，有的则是考虑参数的混合，并且获得了一些实验效果和收敛性质都比较好的方法[8～13]。

Barzilai和Borwein等[14,15]分别介绍和讨论了无约束问题的谱梯度法，Bingin[16]等提出谱梯度法和共轭梯度法结合的谱共轭梯度法，其迭代公式含有2个可变参数:

该谱共轭梯度法在Wolfe 线搜索下收敛且数值结果较理想。对比传统梯度法，谱梯度算法有很好的加速效果，许多学者也对谱共轭梯度法进行了大量的研究[17～20]。受谱共轭梯度法的启发，笔者给出了一种修正的DY谱共轭梯度法。

2 修正的DY谱共轭梯度法

(4)

(5)

其中，0≤μ1≤μ2。当μ1=μ2=0时，该方法变为传统的DY共轭梯度法。

SMDY算法描述如下：

Step 1 初始化:x1∈Rn，δ∈(0,1)，σ∈(δ,1)，0≤μ1≤μ2,ε≥0,d1=-g1,k=1,若‖gk‖≤ε，停止；

Step 2 计算步长αk满足标准的Wolfe非精确线搜索准则:

(6)

(7)

Step 3 置xk+1=xk+αkdk，若‖gk+1‖≤ε，停止迭代；

Step 5 置k=k+1，转Step 2。

3 修正算法的全局收敛性

算法的全局收敛性证明以下列假设条件为基础：

(H1)f(x)在水平集Ω={x∈Rn|f(x)≤f(x1)}有界，其中x1为初始点；

(H2)f(x)在Ω的某邻域Ω1内连续可微，且其梯度函数g(x)满足Lipschitz条件，即存在常数L>0，使得对∀x,y∈Ω1，有：

‖g(x)-g(y)‖≤L‖x-y‖

(8)

并假定‖gk‖≠0，否则目标函数的稳定点已获得，算法终止。

证明用数学归纳法证明。

则：

(9)

故引理1得证。

引理2若αk满足Wolfe非精确线搜索条件式(6)和式(7)，则：

(10)

证明由式(4)可知：

故引理2得证。

引理3若目标函数f(x)满足假设条件(H1)(H2)，则SMDY算法产生的序列{gk}和{dk}满足Zoutendijk条件:

证明由式(7)和式(8)可得：

从而可得：

结合式(6)和式(10)，可得：

(11)

对式(11) 从k=1,2,3,…求和：

并由假设(H1)知f(x)在Ω有界，可得：

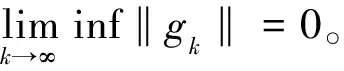
证明用反证法证明。假设定理1结论不成立，则存在常数c>0，使得对∀k≥1，有：

‖gk‖≥c

由式(3)移项得：

对等式两端分别取模平方，再移项得：

(12)

(13)

反复利用式(13)递推形式和‖gk‖≥c及d1=-g1，可得：

从而：

因而有：

这与引理3矛盾，故定理1得证。

4 结语

在经典的DY算法基础上提出了一种修正的谱共轭梯度算法，在Wolfe非精确线搜索下证明了算法的全局收敛性。由于构造谱参数的过程中引进了2个待定参数，在理论上2个参数只要满足关系要求即可，但是在数值表现上可能会因为不同值的选取而使得数值试验表现不同。

[参考文献]

[1]Fletcher R, Reeves C M.Function minimization by conjugate gradients[J].Comput J,1964, 7: 149～154.

[2] Polak E, Ribière G. Note sur la convergence de mèthodes de directions conjugèes[J].Rev Fr Inform Rech Oper,1969, 3:35～43.

[3] Polyak B T.The conjugate gradient method in extreme problems[J].USSR Comput Math Math Phys, 1969, 9: 94～112.

[4] Hestenes M R, Stiefel E.Method of conjugate gradient for solving linear equations[J].J Res Natl Bur Stand, 1952,49: 409～436.

[5] Dai Y H， Yuan Y X. A nonlinear conjugate gradient method with a strong global convergence property[J].SIAM J Optim,1999, 10:177～182.

[6] Fletcher R.Practical methods of optimization vol 1: unconstrained optimization[M].New York:Wiley& Sons,1987.

[7]Liu Y, Storey C.Efficient generalized conjugate gradient algorithms[J].Journal of Optimization Theory and Applications, 1991, 69:129～137.

[8] Jiang X Z，Lin H, Jian J B.A hybrid conjugate gradient method with descent property for unconstrained optimization [J].Applied Mathematical Modelling，2015, 39:1281～1290.

[9] Dai Y H, Kou C X.A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search[J].SIAM J Optim,2013,23:296～320.

[10] Jiang X Z， Jian J B. A sufficient descent Dai-Yuan type nonlinear conjugate gradient method for unconstrained optimization problems[J].Nonlinear Dynamics, 2013, 72:101～112.

[11]郑小平，陈忠.一类推广的共轭梯度法及收敛性分析[J].长江大学学报(自科版)，2016，13(34)：1～3.

[12] Jiang X Z， Jian J B.Two modified nonlinear conjugate gradient methods with disturbance fators for unconstrained optimization[J].Nonlinear Dyn,2014,77(1-2):387～394.

[13]王开荣,高佩婷.建立在 DY法上的两类混合共轭梯度法[J].山东大学学报(理学版),2016,51(6):16～23.

[14] Barzilai J， Borwein J M.Two-point step size gradient methods[J].IMA J Numer Anal,1988, 8(1):141～148.

[15] Raydan M.The Barzilain and Borwein gradient method for the large scale unconstrained minimization problem[J].SIAM J Optim, 1997,7:26～33.

[16] Birgin E G， Martínez J M.A spectral conjugate gradient method for unconstrained optimization[J].Appl Math Optim,2001,43:117～128.

[17]汪丹戎,陈忠,张毅.求解无约束优化问题的一种新的谱共轭梯度法[J].长江大学学报(自科版),2015,12(31)：6～8,40.

[18] 王华军,王硕,曹义超.求解线性逆问题的谱共轭梯度法[J].广西科学,2016,23(5):416～421,427.

[19] 林穗华.Wolfe线搜索下的修正FR谱共轭梯度法[J].山东大学学报(理学版),2017，52(4):6～12.

[20] Jian Jinbao, Chen Qian, Jiang Xianzhen,et al.A new spectral conjugate gradient method for large-scale unconstrained optimization[J].Optimization Methods and Software,2017,32(3):503～515.