基于神经网络和小载荷的疲劳损伤计算
2018-07-06赵冲王碧霞罗竞波祝帆李美求
赵冲,王碧霞,罗竞波,祝帆,李美求
机械零件在服役过程中,承受的载荷往往是随机和反复多次的,绝大部分的失效模式是疲劳失效。当下应用最广泛的疲劳损伤理论是线性疲劳累积损伤理论,即Miner理论[1]。该理论认为材料在各个应力下的损伤是独立进行的,并且总损伤可以线性地累加起来[2]。因其简单易操作而受到生产实际的欢迎,但该理论没有考虑低于疲劳极限的小载荷和加载顺序对疲劳损伤累积的影响,计算结果往往与实验的损伤结果有较大的偏差。王旭亮等[3]提出的模糊疲劳损伤理论将应力模糊带的上边界置于疲劳极限处,对小于原来疲劳极限的应力也考虑其产生的损伤,但没有考虑小载荷的强化作用和载荷顺序的影响。王正等[4]建立了随机载荷循环作用下的结构疲劳寿命预测模型,分析了结构所受循环载荷作用的不确定性特征,并采用泊松随机分布来描述零件的动态可靠性模型[5],但未考虑载荷之间相互影响,得到的机械结构疲劳寿命预测模型和零件动态可靠性模型与实际结果依然有较大误差。为此,笔者提出一种将非齐次泊松过程理论与小载荷及其不确定性和伴随损伤相结合来计算疲劳损伤量的方法。
1 传统疲劳累积损伤理论
传统疲劳累积损伤理论的基本假设[6]如下:
1)在任何等级载荷的作用下,零件都将产生疲劳损伤,其疲劳损伤的严重程度除了与该级载荷工作的循环次数有关外,还与该级载荷作用下产生疲劳失效的总循环数有关;
2)每一级载荷产生的疲劳损伤是相互独立且永存的,并且在不同载荷下循环工作所产生的累积总损伤等于各级载荷水平下的损伤线性累加。
第1条假设,任何循环应力都能产生损伤。在与疲劳有关理论的研究中,高于疲劳极限的载荷称为大载荷,低于疲劳极限的载荷称为小载荷,郑松林等[7]在对汽车前轴的实验中指出,存在一个低载区,该区间的小载荷反复作用,将使结构的疲劳强度得到不同程度的提高。大多数机械零件在实际工作过程中,受载是连续多变的且往往能跨越各个损伤分界点,而疲劳损伤显然也是一个连续累积的过程,在各个载荷历程采用同一种损伤计算方式显然是不合适的,因此,计算疲劳损伤必须分段处理。
第2条假设,不同应力幅下循环工作所产生的累积总损伤等于每一应力水平下的损伤之和。文献[8]中大量试验事实显示,分别采用L-H加载顺序和H-L加载顺序得到的疲劳总损伤差别很大,即疲劳损伤不能仅以各级载荷下的损伤简单地线性相加。
针对以上不足,笔者将求解疲劳损伤过程划分为3个不同阶段分别求出损伤再累加,并在大载荷区间考虑载荷作用次序的影响。
2 随机过程模型的数学描述
在整个机械系统中,各个零件承受载荷出现的过程是一个计数过程,时间间隔(t0,t)内出现的载荷次数与下限时间t0前出现的载荷无关,每时每刻出现的载荷是随机变化的,且载荷随时间的变化不是一个平稳增量的过程,因此,可以用非齐次泊松过程描述[9~11]。
假设N(t)为到时刻t为止载荷出现的总次数,且N(t)满足以下条件:
1)N(0)=0;
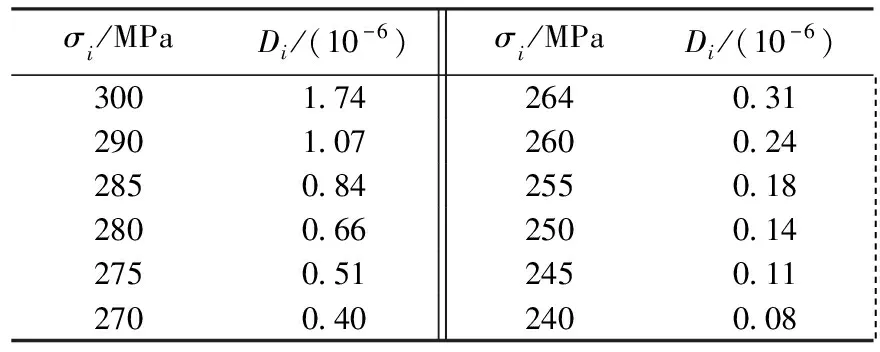
2)在任意时间段内载荷出现相互独立,即任取0 3)对于任意t>0和充分小的Δt>0,有: 现场的机械零件所受载荷一般满足以上几点,即服从参数为{λ(t)>0,t≥0}的非齐次泊松随机分布,数学描述如下: (s,s+t)时间内荷载出现n次的概率: (1) 对载荷进行分级处理,各级载荷出现的概率: (2) 当s=0,n=1时,各级载荷出现一次的概率: P0[Ni(0+t)-Ni(0)=1] =Λi(t+x)exp(-Λi(t+x)) (3) 显然,式(3)的值在(0,1)之间波动,并且靠近区间下限,由麦克劳林公式: (4) 得: =Mexp(-M) =M×[1-M+o(-M)] =M-M2+o(M2) =M+o(M) (5) 图1 自适应线性神经网络结构 笔者采用神经网络参数估计法[12]对上述模型参数进行估计。幂律模型经过对数化处理可以转化为线性关系,故选用自适应线性单层神经元网络模型结构。 1)神经元计算模型 自适应线性神经网络结构如图1所示。输入矢量P的每个元素pj(j=1,2,…,r),通过权矩阵W与每个输出神经元相连(即全联接);每个神经元通过一个求和符号,在与输入矢量进行加权求和运算后,形成激活函数的输入矢量,并经过激活函数f(·)作用后得到输出矢量A,它可以表示为: As·1=F(Ws·r·Pr·1+Bs·1) (6) 自适应线性网络的激活函数为线性函数,因而: As·1=Ws·r·Pr·1+Bs·1 (7) 式中,Bs·1为偏差矢量;s为神经元的个数;r为输入矢量的位数;F(·)表示激活函数。 当s=1时,网络全矩阵为: W1·r=(w11,w12,…,w1r) (8) 2)W-H学习规则 线性神经元网络采用的是W-H学习规则,又叫δ规则或最小均方差算法(LMS)。 首先定义一个线性网络的输出误差函数: (9) 式中,T为目标矢量。 根据梯度下降法,权矢量的修正值正比于当前位置上E(W,B)的梯度,对于第i个输出节点有: (10) 或表示为: Δwij=ΔbipjΔbi=ηδi (11) 这里,η为学习效率;δi定义为第i个输出节点的误差: δi=ti-ai (12) 在一般的实际运用中,η通常取一接近1的数,或取值为: (13) 各级载荷所对应的λi(t)求法相同,只需改变相应的统计载荷σi,因此,笔者只介绍λ(t)的算法。 对于机械问题,非齐次泊松强度函数λ(t)采用幂律模型[13]确定较为合适: λ(t)=λβtβ-1 (14) 式中,λ为对应齐次泊松强度系数;β为幂律模型变化参数。 如前所述,在时间(0,t)内的均值为: (15) 对式(15)两端同时取对数,可得: lnm(t)=lnλ+βlnt (16) 令y=lnm(t),x=lnt,a=lnλ,则式(16)可简化为: y=a+βx (17) 图2 神经网络结构设计 这是一条斜率为β、截距为a的直线。神经网络的结构如图2所示。 记神经网络的输入矢量和目标矢量分别为X,Y: X=[x1,x2,…,xn]T (18) Y=[y1,y2,…,yn]T (19) 其中,xi=lnti;yi=lnm(ti);ti为第i次统计时间;n为统计次数。 将统计所得数据按照神经网络参数估计法得到: (20) 对于随机载荷问题,各个时刻各级载荷的出现均有一定的概率,采用最大顺序统计量的方法显然不合适,故而需要对时刻t的载荷进行等效处理,即t时刻的当量载荷为: (21) 图3 低幅载荷的分区 在疲劳损伤计算时,常以疲劳极限为界,疲劳极限以下的载荷称作小载荷,反之,则为大载荷[14]。机械零件经历一个完整的时间载荷历程,往往需要承受大小循环载荷的作用。现用的疲劳损伤理论模型绝大部分都不考虑小载荷的影响,而只认为大载荷才对损伤有贡献。事实上,能够造成损伤的小载荷可以低到0.5倍的疲劳极限σe,另外,疲劳试验表明,对于小载荷,存在一个低幅交变载荷区,如图3所示。该区间的载荷反复作用于零件或结构,将使其疲劳强度得到不同程度的提高,这种现象被称为低载强化[15]。 下面,笔者基于均匀损伤计算零件在随机载荷作用下的总损伤。因谱载荷作用下的任一级应力均不是独立的,前后应力间的耦合作用会对材料的损伤和寿命产生较大影响,故而计算损伤应分段考虑。 选取材料的疲劳极限σe为分界点,对于大载荷,主要考虑载荷之间的顺序效应和相互影响;单次循环载荷产生的损伤DA称为伴随损伤[8],可以分为2部分:一部分为不影响损伤但反映该次循环应力损伤水平的视在损伤DT,主要作用是改变损伤历程;另一部分为影响损伤的耦合损伤DC,其值与载荷作用顺序及当前应力产生的损伤有关。对于小载荷,基于隶属函数考虑其强化损伤Ds,对于载荷历程中处于无强化作用区的小载荷,其损伤强化效果均可忽略,固取其有强化作用区的下限σL=0.7σe。隶属函数的选取可以根据所研究问题的性质选用某种典型的函数形式,其参数也可根据需要满足的条件而定。损伤值属于偏大型模糊分布[16],隶属函数μΘ(σi)是在论域[0,σe)上的有界单调递增函数,其值域为[0,1]。 综上所述,当σi∈[0,σL)时: μΘ(σi)=0Di=0 (22) 当σi∈[σL,σe)时: (23) 当σi∈[σe,σM]时: (24) (25) 联立式(22)、(23)、(24)、(25)得出谱载荷下的总损伤D: (26) 以45钢为材料的试件进行动态随机加载疲劳试验,试验中所设定的8级应力幅值水平分别为:σ1=275MPa,σ2=270MPa,σ3=265MPa,σ4=260MPa,σ5=255MPa,σ6=250MPa,σ7=245MPa,σ8=240MPa。平均应力σm=0,应力比r=-1,疲劳极限σe=244MPa,试验中设定载荷随机加载程序,不断地对试件进行动态循环加载,直至试件发生破环。 依据文献[17]提供的载荷数据,利用Matlab软件的rand函数产生的随机数模拟试件承受的载荷,其受载矩阵P如下: 采用非齐次泊松过程与小载荷理论和伴随损伤相结合的方法对试件的损伤值进行估算,再将估算结果与试验结果进行比对,以验证该估算方法的可行性。损伤估算具体步骤如下: 1)依据45钢的S-N曲线[17]: σ13.711N=1039.736 (27) 得到各级载荷下的单次循环损伤值,如表1所示。 表1 各级载荷单次循环损伤表 2)利用步骤1)中的载荷数据输入到神经网络模型的输入层,得到各个统计时刻的λi(t)值,进而依据式(21)计算各个时刻的当量载荷值。 3)对于小载荷,其隶属度函数选用升半梯形分布,即: (28) 4)根据式(26)计算试件发生疲劳破环时的损伤值。将获得的数据采用前述方法计算所得的参数带入式(26)积分,可以求出在载荷循环8.080×106次时的损伤和为0.92。 从理论意义上来说,一个试件从生产出来到疲劳破环的整个生命周期中,损伤值必定在区间[0,1]上单调上升,破环时的损伤和,即临界损伤和D=1。特别地,修正的Miner理论其临界损伤和D=1.47。 通过Miner线性疲劳损伤理论计算的疲劳损伤和D=1.71,误差为71%;通过修正的Miner理论计算得到的疲劳损伤和D=2.24,误差为52%;通过笔者提出的方法进行计算,得到的疲劳损伤和D=0.92,误差仅为8%。由此可以看出,基于神经网络的考虑小载荷的泊松过程的方法能够更好的描述损伤累积过程,使材料的疲劳损伤更加接近实际情况。 1)运用非齐次泊松过程理论对机械零件所受各级载荷的概率进行模拟分析,应用“当量载荷”代替传统的“最大载荷”计算零件的损伤,同时,采用神经网络的方法估计非齐次泊松随机过程的幂律模型参数,避免了对于微观变幅载荷过程求解路径难以选择的问题。 2)从理论意义上讲,非齐次泊松过程对于随机载荷的模拟是比较合理的,在求解损伤的过程中,充分考虑了小载荷的影响,同时对于载荷微观变幅过程中各级载荷之间的相互影响问题也给予了充分的说明,并以8级载荷的随机过程试验数据进行验证,误差仅为8%,相比于传统的方法误差大幅降低,表明采用笔者提出的计算方法对随机载荷产生的损伤计算更为精确。 [参考文献] [1]夏天翔,姚卫星,刘向民,等.考虑材料分散性后Miner理论在多轴两级阶梯谱下的适用性研究[J]. 机械工程学报,2015,51(14):38~45. [2] 张小丽,陈雪峰,李兵,等. 机械重大装备寿命预测综述[J]. 机械工程学报,2011,47(14):100~116. [3] 王旭亮,聂宏. 基于模糊理论的疲劳寿命估算方法[J]. 中国机械工程,2008,19(17):2095~2097. [4] 王正,谢里阳,李兵. 随机载荷作用下的零件动态可靠性模型[J]. 机械工程学报,2007,43(12):21~22. [5] 王正,王增全,何洪. 随机载荷循环作用下的机械结构疲劳寿命预测模型[J]. 中国机械工程,2012,23(1):98~99. [6] 秦大同,谢里阳. 疲劳强度与可靠性设计[M]. 北京:化学工业出版社,2013. [7] 郑松林,梁国清,王治瑞,等.考虑低幅锻炼载荷的某轿车摆臂载荷谱编制[J]. 机械工程学报,2014,50(16):147~154. [8] 温洁明,陈国军,陈家权,等. 沙堆疲劳损伤累积模型的研究[J]. 广西大学学报(自然科学版),2011,36(2):257~262. [9] Ove D. Stochastic model for joint wave and wind loads on offshore structures[J]. Structural Safety, 2002, 24: 139~163. [10] LI Jianping, Thompson G. A method to take account of in-homogeneity in mechanical component reliability calculations[J]. IEEE Transaction on Reliability, 2005, 54(1): 159~168. [11] 米良,程珩,权龙. 基于泊松随机过程的风力发电机叶片疲劳寿命估算[J]. 机械工程学报,2016,52(18):135~136. [12] 丛爽. 面向Matlab工具箱的神经网络理论与应用[M]. 合肥:中国科技大学出版社,2009. [13] 张勇,邱静,刘冠军,等. 基于非齐次泊松过程和统计仿真的故障样本模拟生成[J]. 机械工程学报,2012,48(15):77~79. [14] 吴卓,刘晓芬. 基于变幅小载荷下的曲轴疲劳寿命预测分析[J]. 机械制造,2013,51(12):54~56. [15] 邹喜红,杨真亮,袁冬梅,等. 考虑低载强化效应的变速器加速试验谱的编制[J]. 机械传动,2016,40(4):4~9. [16] 左芳君.机械结构的疲劳寿命预测与可靠性方法研究[D].成都:电子科技大学,2016. [17] 黄海鑫. 随机加载疲劳试验及其寿命估算研究[D]. 南宁:广西大学,2014.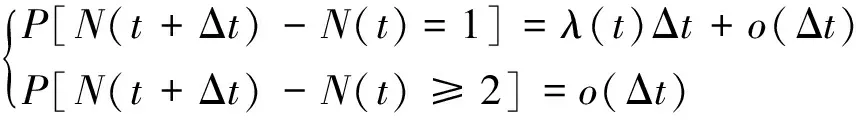


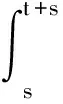
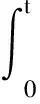
3 非齐次泊松过程参数估计
3.1 自适应线性单层神经元模型

3.2 参数估计

3.3 当量载荷
4 随机载荷作用下的损伤计算


5 45钢随机载荷作用下的损伤计算

6 结论
