M-矩阵最小特征值的新下界

李艳艳

（文山学院 数学学院，云南 文山 663099）

1 预备知识

若矩阵的所有元素都非负，就称为非负矩阵，记作A≥0，ρ(A)表示A的谱半径；若是矩阵的非主对角元素非正，且逆矩阵为非负矩阵，就称A为M-矩阵，τ(A)表示A的最小特征值，且有性质CD=(cijdij)，称为C和D的Hadamard积。

设B=(bij)是M-矩阵，引入如下一些符号

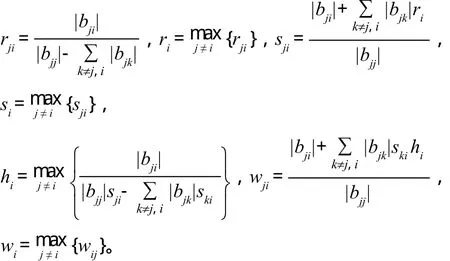
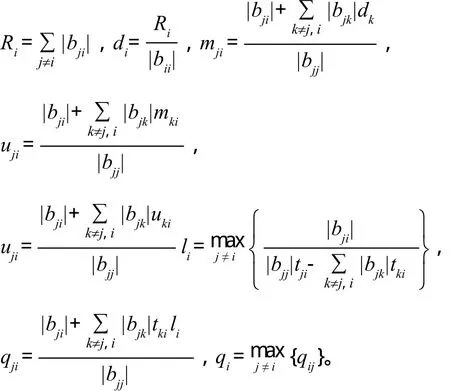
引理1[1]设E，D，H∈Rn×n，其中E，D是正对角矩阵，I为单位矩阵，则

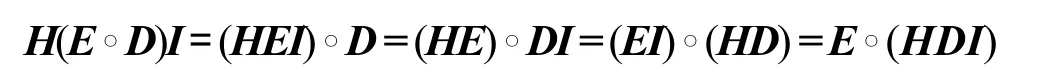
引理2[2]设H=(hij)为任意的n阶方阵，则H的特征值都位于区域

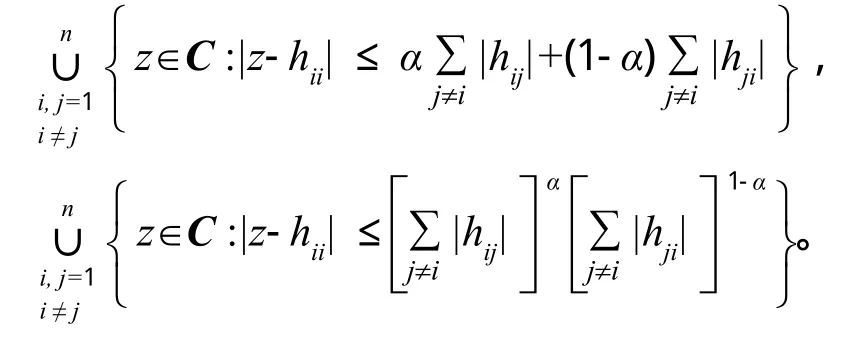
引理3[3]设B=(bij)∈Rn×n是行严格对角占优M-矩阵，则B-1=(βij)满足

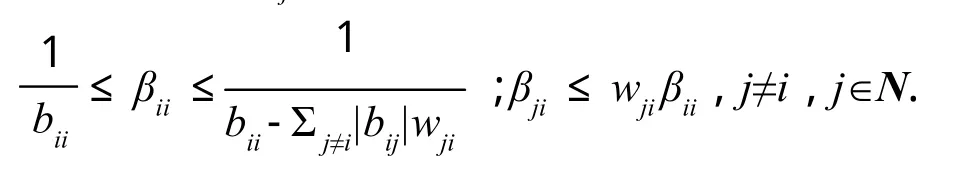
引理4[4]设B=(bij)∈Rn×n是行严格对角占优M-矩阵，则B-1=(βij)满足

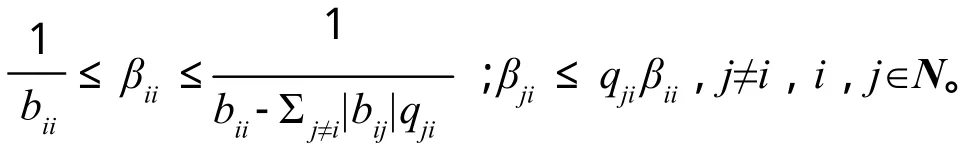
2 主要结果

首先利用非负矩阵和矩阵Hadamard积的性质，构造了不改变矩阵谱半径的非负矩阵，其次通过应用引理2中的圆盘定理，得到了M-矩阵最小特征值的4个只与矩阵元素有关的新估计试。

定理 1 设A=(aij)≥ 0，B=(bij)∈Mn，B-1=(βij)，则有

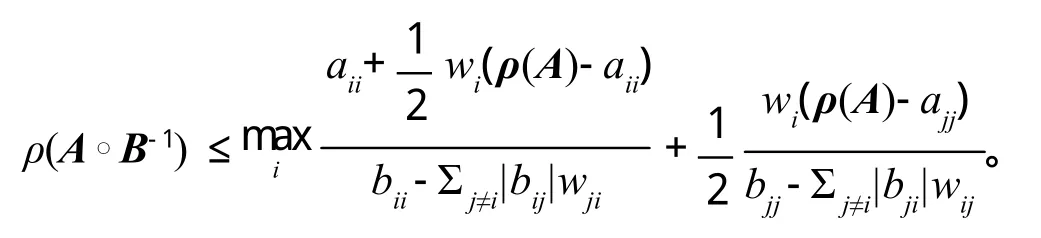
证明 ：令，对于非负矩阵F-1AF，存在正向量v=(v1,v2,…vn)，使得，即

令)，则

且GB-1=(tij)=

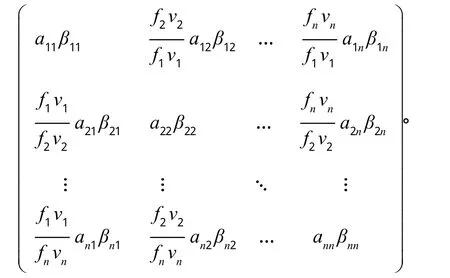
由引理1知，(FV)-1，AB-1(FV)=(FV)-1A(DU)B-1=GB-1，即ρ(AB-1)=ρ(GB-1)=λ。

应用引理2中的第一个特征值包含域知，存在i使得

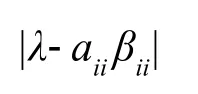
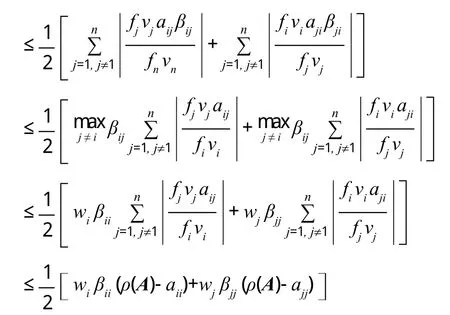
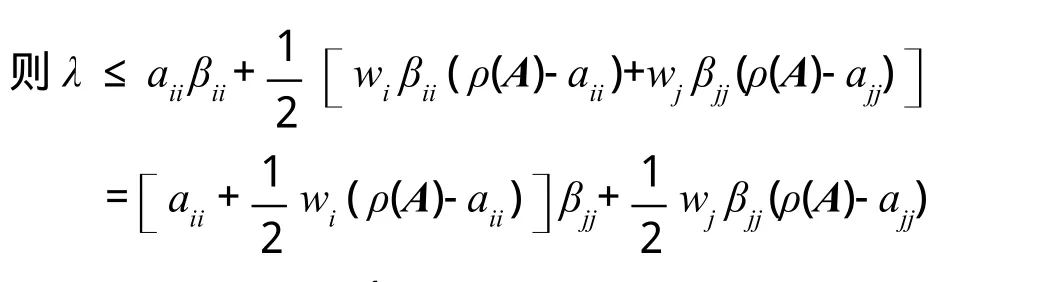
又因为，所以

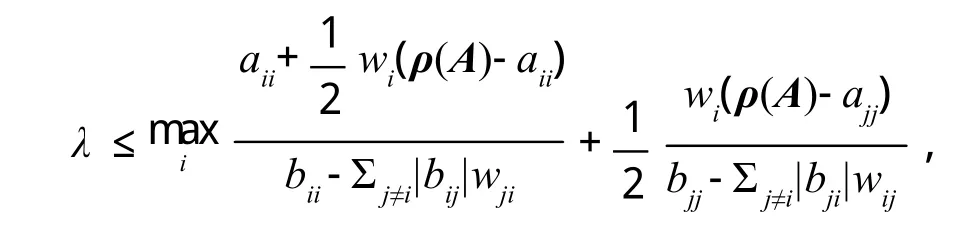
即结论成立。

同理，可得下面的定理2。

定理 2 设A=(aij)≥ 0，B=(bij)∈Mn，B-1=(βij)，则有

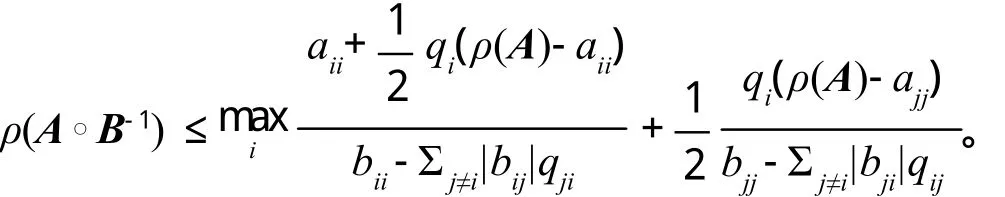
定理 3 设B=(bij)∈Mn，B-1=(βij)，则有

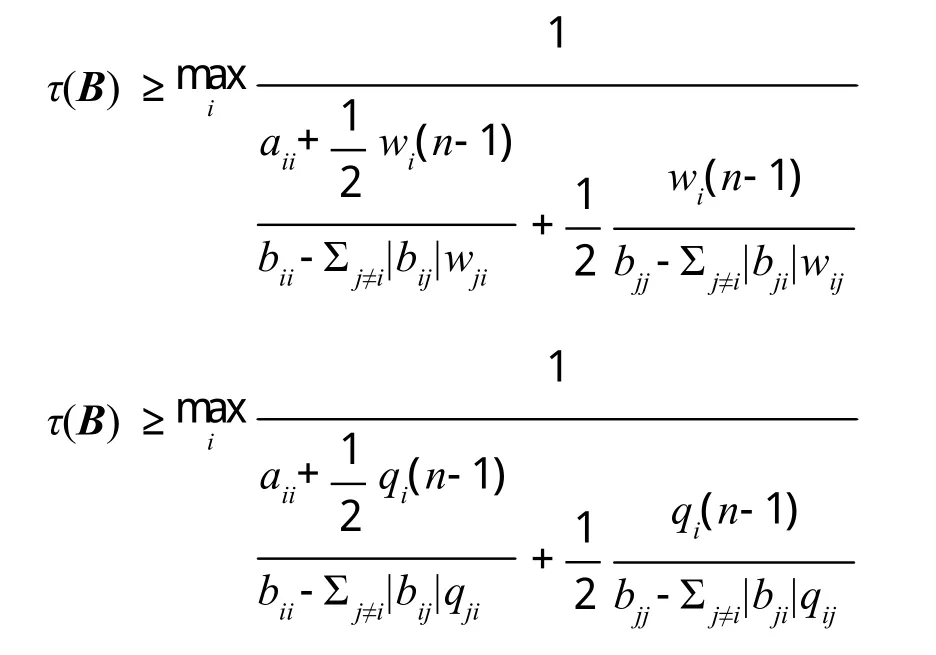
证明：在定理1中令A为元素全为1的矩阵J，则

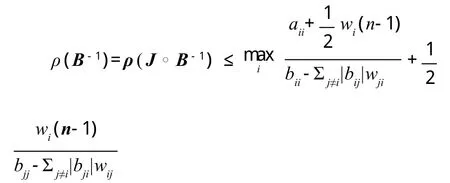
又由矩阵B的性质，得

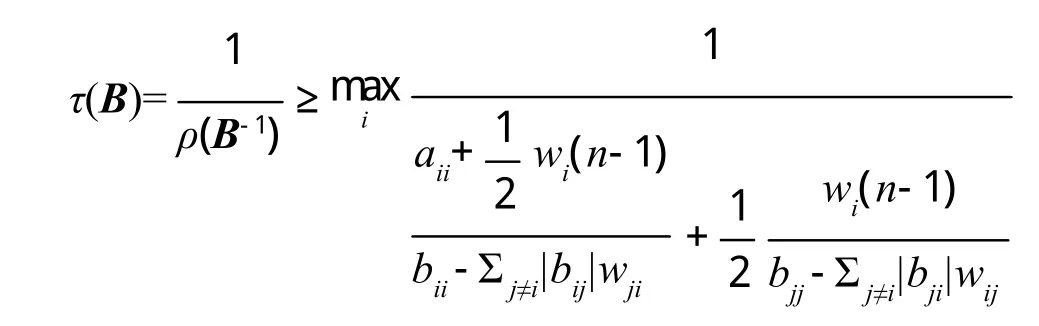
同理可得

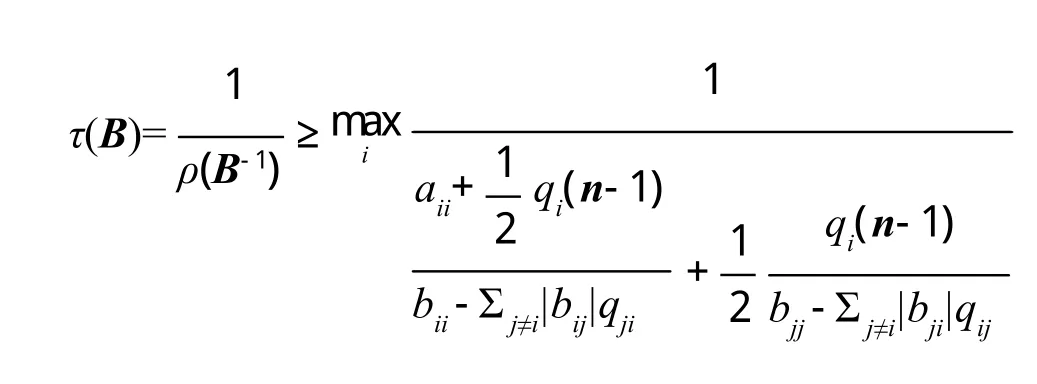
定理 4 设A=(aij)≥ 0，B=(bij)∈Mn，B-1=(βij)，则有

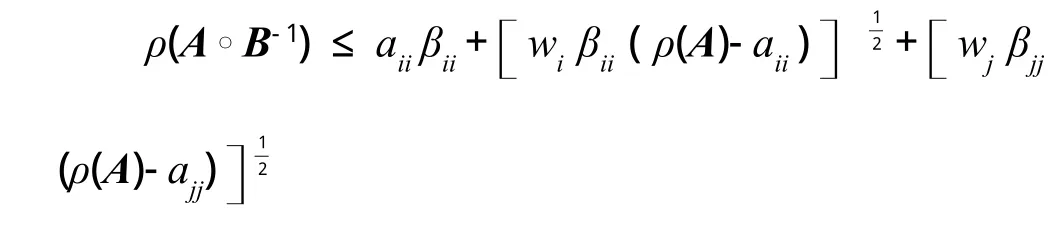
证明：类似定理1的证明，应用引理2中的第二个特征值包含域，知存在i使得

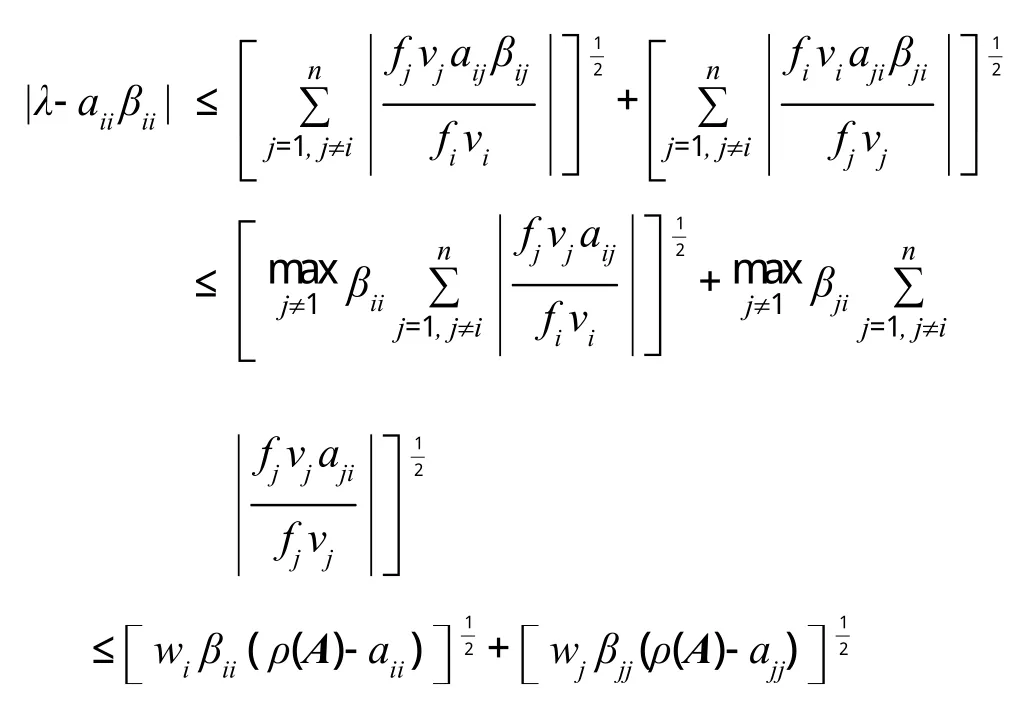
则即

定理 5 设A=(aij)≥ 0，B=(bij)∈Mn，B-1=(βij)，则有

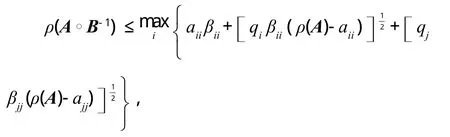
定理 6 设B=(bij)∈Mn，B-1=(βij)，则有

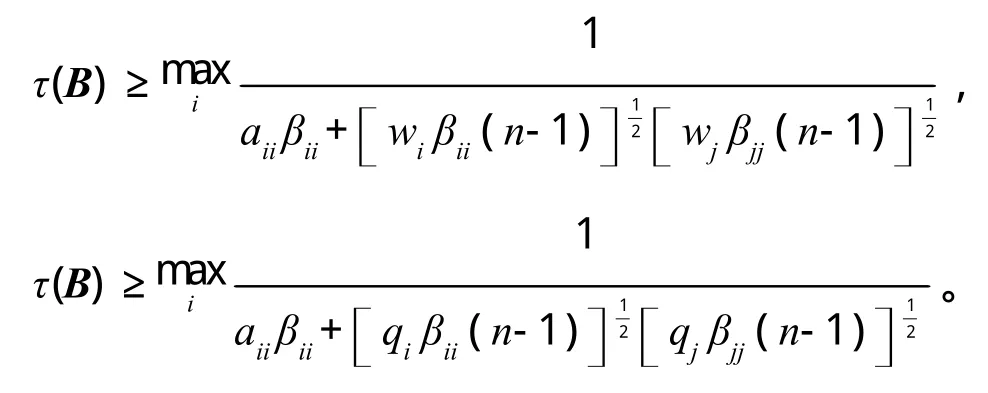
证明：在定理1中令A为元素全为1的矩阵J，则

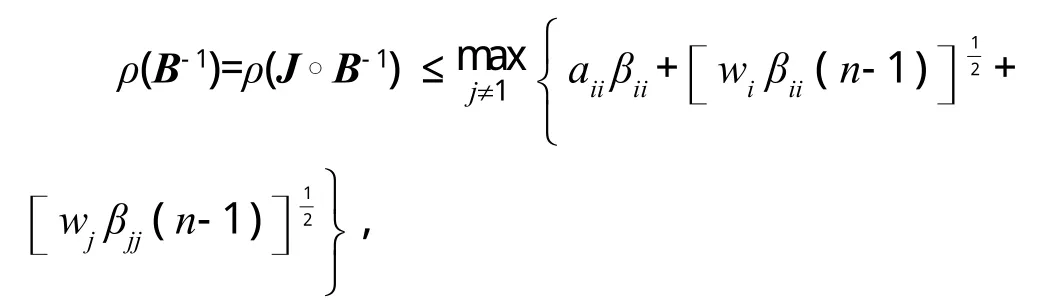
又由矩阵B的性质，得

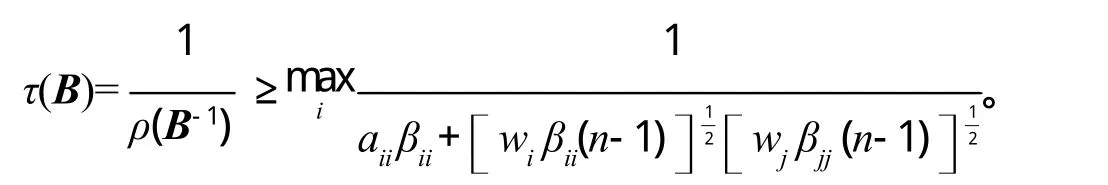
3 数值算例

例1，A是严格对角占优M-矩阵，由定理3，定理6分别得τ(A)≥ 0.1988，τ(A)≥ 0.2013，τ(A)≥ 0.1863，τ(A)≥0.1993，但由文献[5]得τ(A)≥0.1749。该例说明了本文的结果一定情况下改进了现有的估计式。

[1]Horn R A,Johnson C R.Matrix analysis[M].New York:Cambridge University Press,1995：2-24.

[2]Horn R A,Johnson C R.Topics in Matrix analysis[M].New York: Cambridge University Press,1991：34-49.

[3]王峰.非奇异M-矩阵的逆矩阵和M-矩阵的Hadamard积的最小特征值下界估计[J].应用数学学报，2013（2）：13-15.

[4]Feng Wang,Deshu Sun.New bounds for the minimum eigenvalue ofM-matrices[J].Open Mathematics Research Article,2016,14:1007-1013.

[5]Chaoqian Li,Yaotang Li,Ruijuan Zhao.New inequalities for the minimum eigenvalue ofM-matrices[J].Linear and Multilinear Algebra,2013(9)：1267-1279.