DYNAMICS OF A PREDATOR-PREY REACTION-DIFFUSION SYSTEM WITH NON-MONOTONIC FUNCTIONAL RESPONSE FUNCTION∗†
2018-07-06HuanWangCunhuaZhang
Huan Wang,Cunhua Zhang
(Dept.of Math.,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,PR China)
1 Introduction
Since Lotka[5]and Volterra[13]proposed the classical Lotka-Volterra predatorprey model,the dynamics between predator and their prey have drawn great attention of many researchers including mathematicians and biologists.The functional response function included in the classical Lotka-Volterra predator-prey model is linear through the origin and therefore is unbounded.In the research of the predatorprey systems,however,people recognized that the functional response of predator,in some case,is nonlinear and bounded.Thus a more reasonable predator-prey system should include a nonlinear and bounded functional response function.Let u and v denote the population densities of prey and predator species at time t,respectively.Then the dynamics between predator and prey species should be described by the following model[3,7,8,14]

where K is the most existent capacity of prey and D is the death rate of predator.The function g(u,K)represents the growth rate of prey in the absence of predator and is assumed to satisfy the following conditions when u≥0 and K>0:

The form most often used for g(u,K)is the so-called Logistic growth of the form g(u,K)=1−.The predator response function p(u),in general,is a continuously differentiable function defined on[0,∞)and satisfies
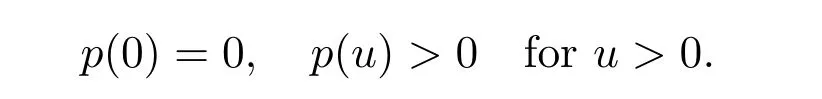
To describe the group defense of prey species,it is assumed that there exists a constant M>0 such that
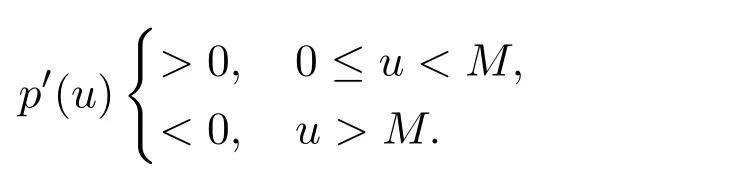
The function q(u)represents the rate of conversion of the captured prey to predator and,generally,in the models of Gauss type,q(u)is taken as cp(u)where c is a positive constant.
According to the above properties of the response function p(u),Andrews[1]proposed the following Monod-Haldane(also called Holling type-IV)response function:

where m>0 represents the maximal growth rate of the species,a>0 is the half saturation coefficient and b is a positive constant.On the basis of the response function(1.2),Sokol and Howell[12]in 1981 suggested the simplified form of(1.2),namely,

By taking g(u,K)=1−and p(u)as the form(1.3),Ruan and Xiao[11]considered the following prey-predator system
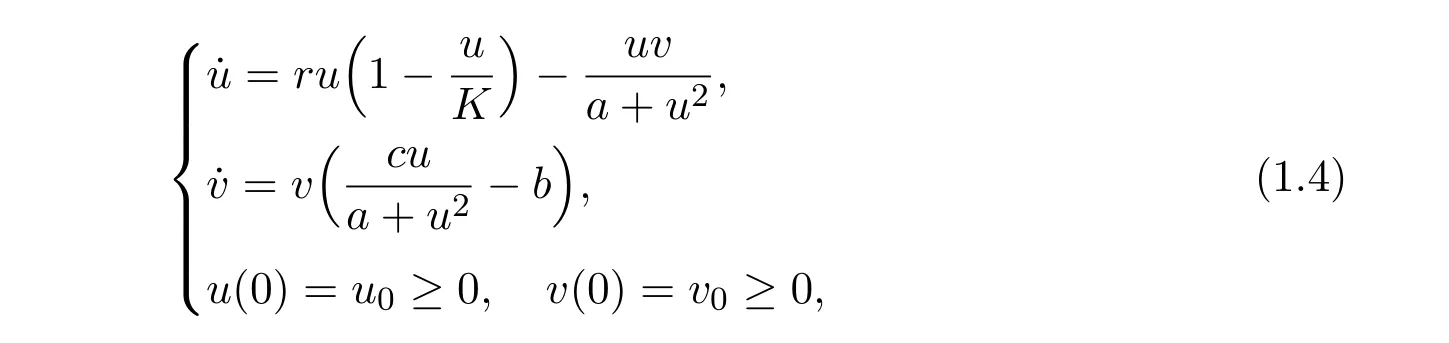
where r is the intrinsic growth rate of prey.It is noticed that the population models described by ordinary differential equations were always proposed under the assumption that the distribution in space of the species are homogeneous.In practice,this is not the case and consequently a more reasonable population model should be described by reaction-diffusion equations.Based on this fact,the population system corresponding to(1.4)should be described by the following reaction-diffusion system
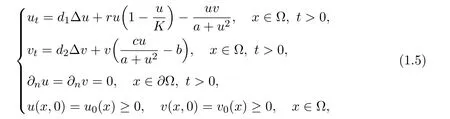
whereΩ ⊂ RN(N ≥ 1)is a bounded domain with a smooth boundary∂Ω,∆denotes the Laplace operator,n is the unit outward normal vector on ∂Ω,∂nis the direction derivative at the point x on∂Ω along the direction n and di>0(i=1,2)represent the diffusion coefficients of two species.Recently,Pang and Wang[9]investigated roughly the local asymptotic stability of the constant positive steady state and analyzed in detail the existence and non-existence of non-constant positive classical solutions of the reaction-diffusion system(1.5).
When the parameters r,a,b and c in system(1.4)are fixed,Ruan and Xiao[11]studied the global qualitative and bifurcation analysis of(1.4)such as the saddlenode bifurcation,the supercritical and subcritical Hopf bifurcation,and the homoclinic bifurcation by choosing K as the bifurcation parameter.In addition,the existence of Bogdanov-Takens bifurcation of system(1.4)was also discussed in[11]and the normalform for the Bogdanov-Takens bifurcation was obtained by regarding K and D as the bifurcation parameters.A natural question is that how the parameters a,b and c affect the dynamics of system(1.4)when K is fixed.In order to discuss this problem and consider the effect of the spatial diffusion on the dynamical behaviors of system(1.5),we shall take K=1 and consider the following system
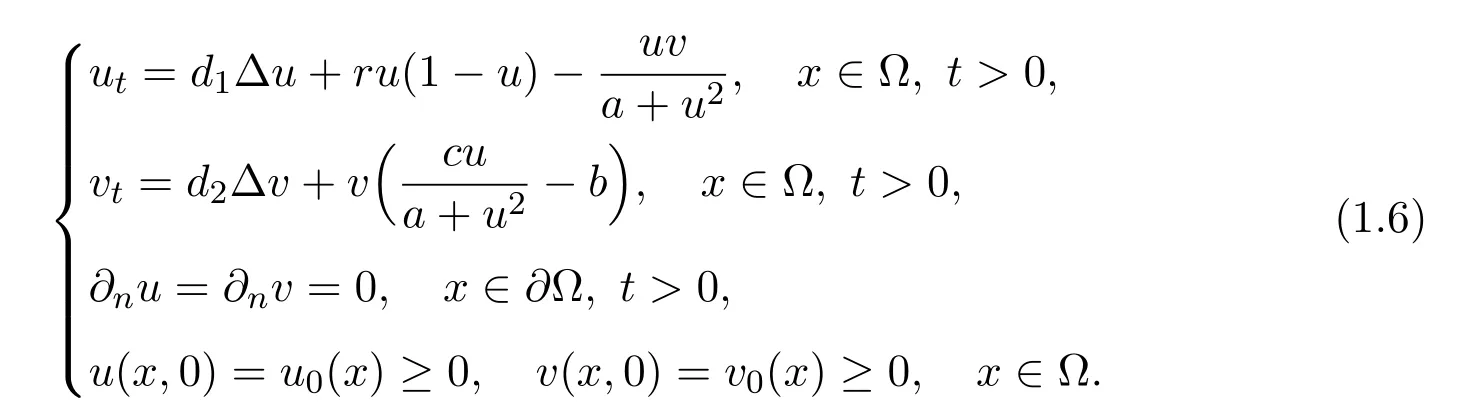
This paper is organized as follows.In Section 2,by means of the basic theory for dynamical systems,the local asymptotic stability,the instability and the existence of Hopf bifurcation of the positive equilibria of the local system corresponding to(1.6)are analyzed in detail.The effect of the spatial diffusion on the dynamical behaviors of(1.6)is analyzed in Section 3.To verify the obtained theoretical predictions,some examples and numerical simulations are also included by applying the numerical methods to solve the ordinary and partial differential equations in Section 4.
2 Existence and Stability of Positive Equilibria for the ODE System
In this section,by applying the basic theory of dynamical systems[2,15],we shall consider mainly the existence and stability of positive equilibria of the ODE system corresponding to the reaction-diffusion system(1.6),which reads as
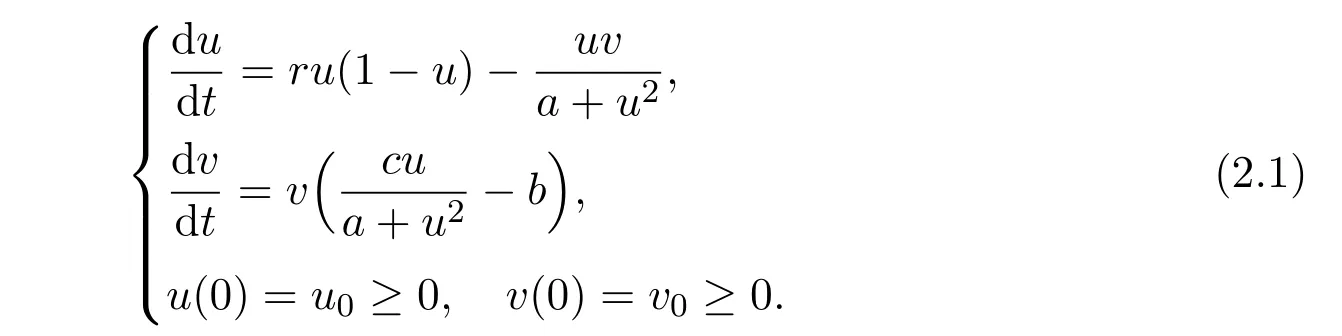
2.1 Existence of positive equilibria
It is easy to observe that the positive equilibria of system(2.1)should be the positive solutions of the following algebraic equations
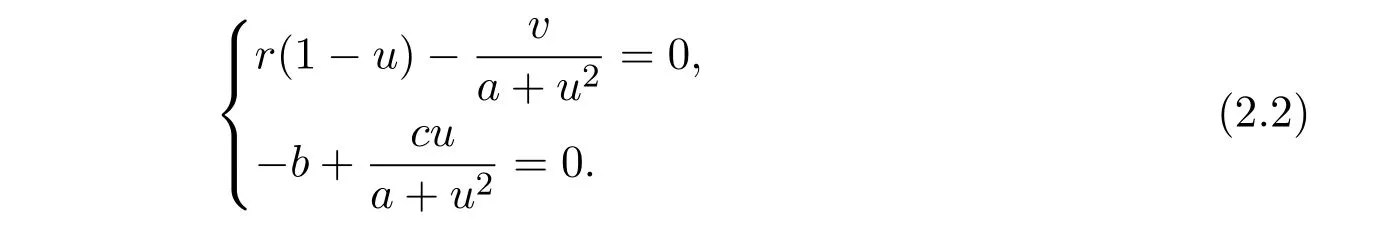
The second equation in(2.2)is equivalent to the following quadratic equation

(i)If c2−4ab2<0,then equation(2.3)has no real root.Therefore,model(2.1)has no positive equilibrium.
(ii)If c2−4ab2=0,that is,c=then equation(2.3)has a double root
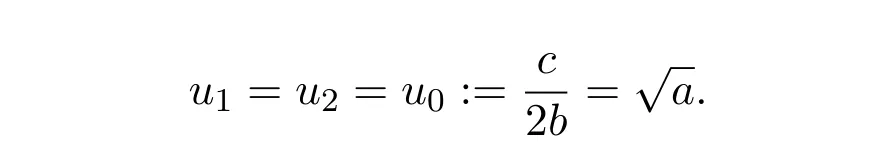
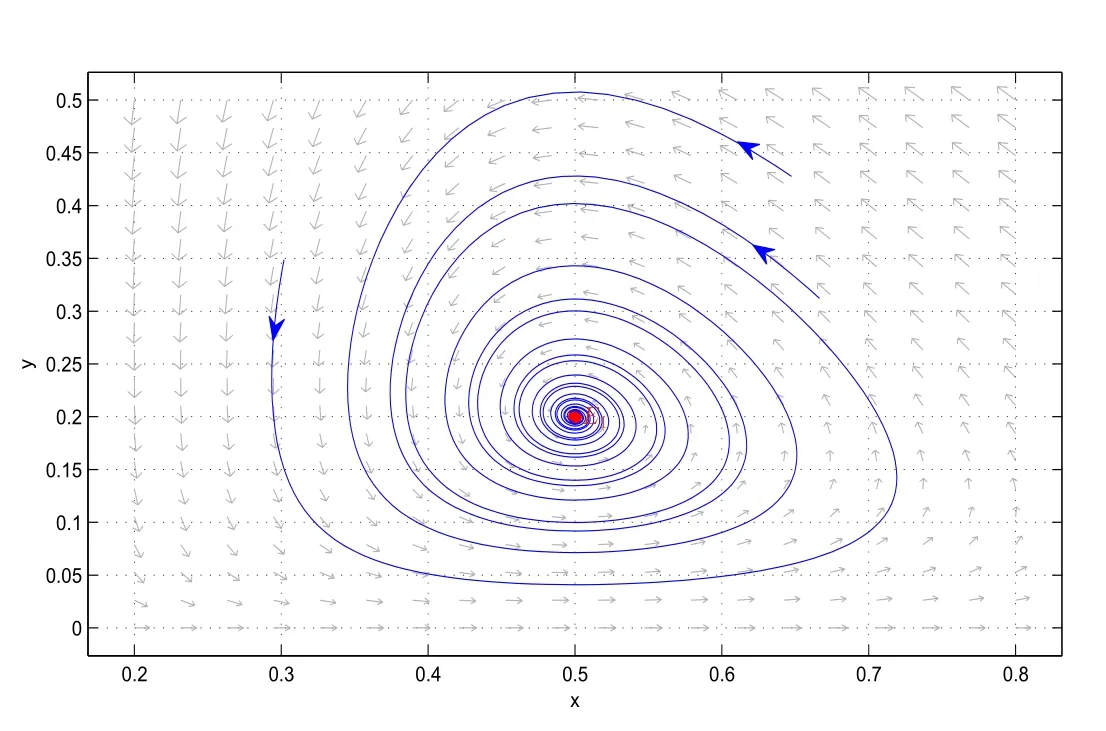
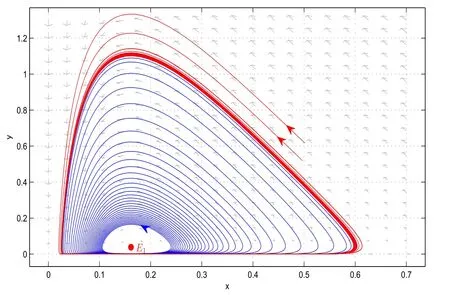
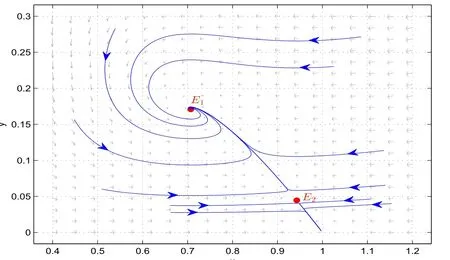
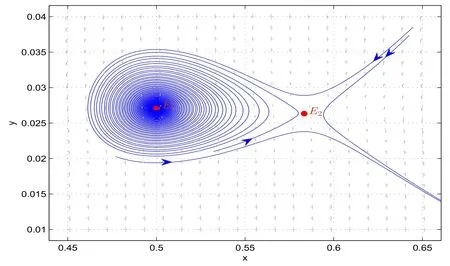
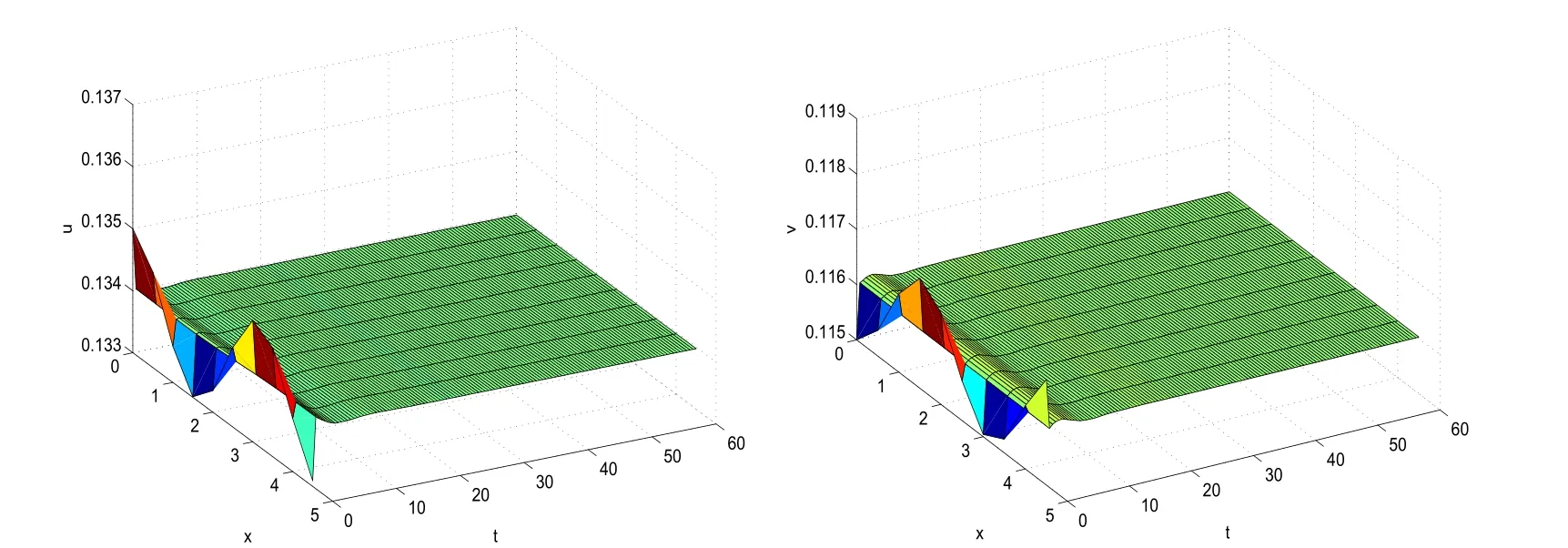
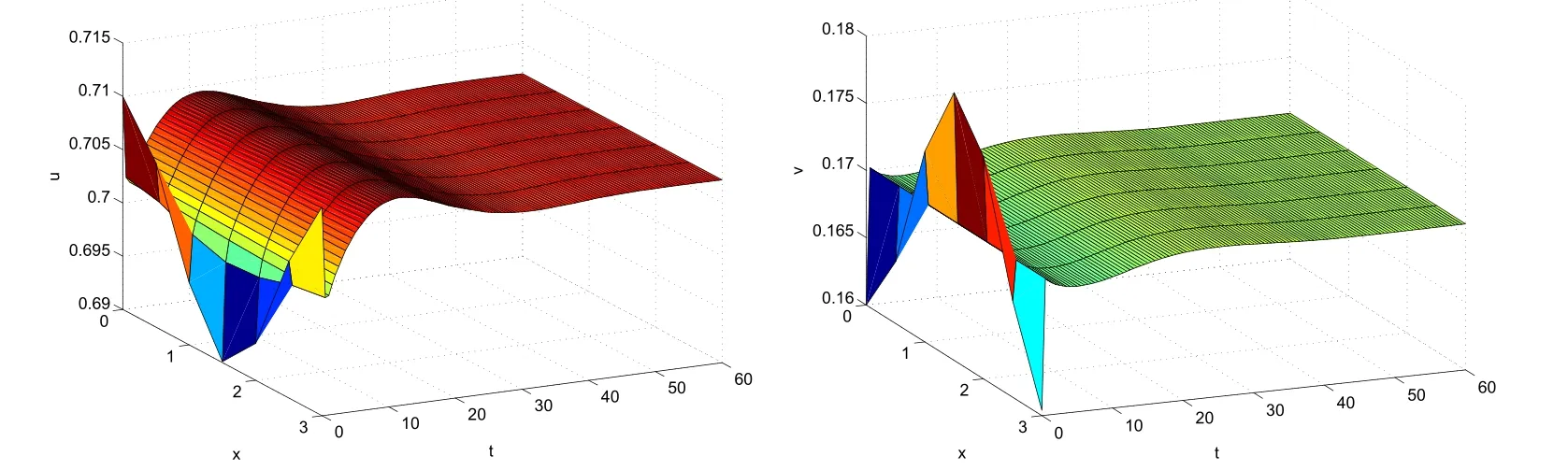
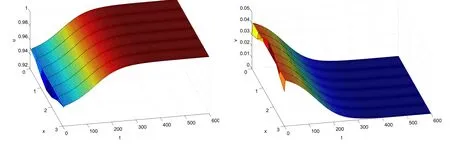
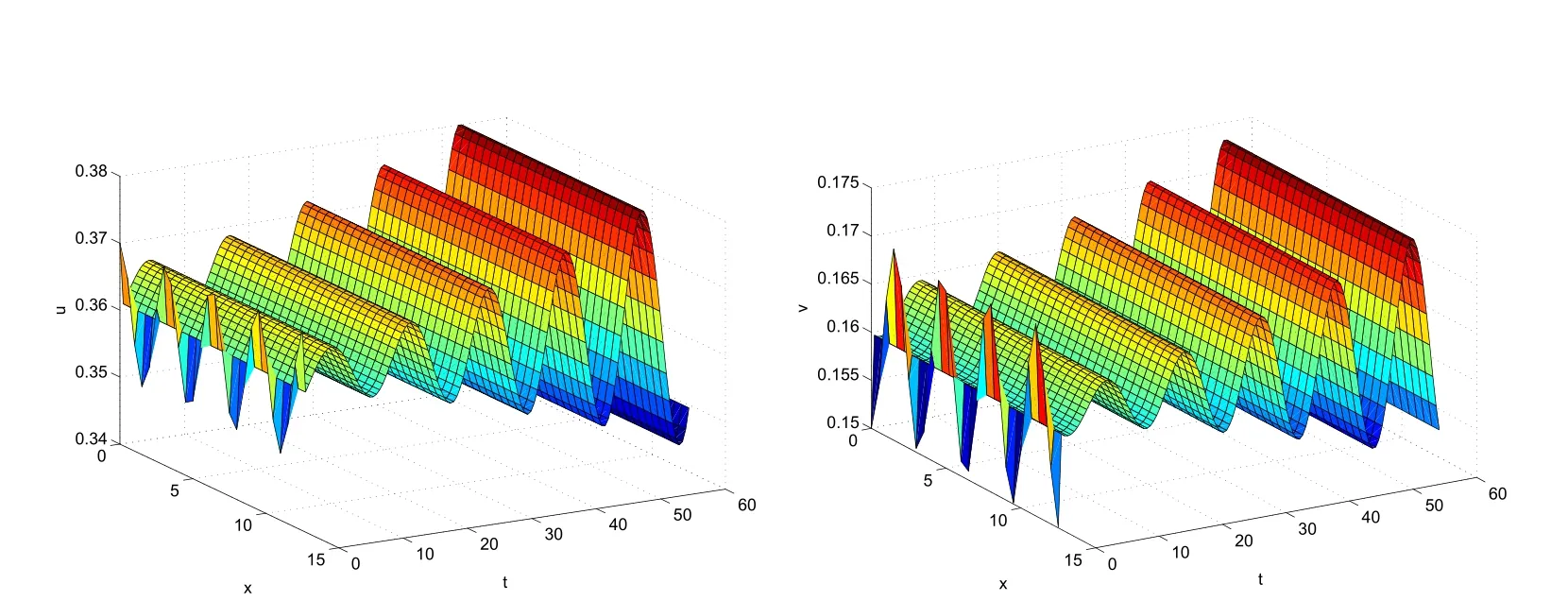
It is easy to see that system(2.1)has no positive equilibrium when a≥1 and possesses a unique positive equilibrium(u0,v0)when 0 (iii)If c2−4ab2>0,that is,c>2then equation(2.3)has two realpositive roots If uk(k=1,2)<1,we know that system(2.1)has a positive equilibrium(uk,vk),where Thus we have It follows that (ii)If c>(a+1)b,then c>.Therefore,we have that is, Thus one can get It is easy to obtain from the above inequality that (iii)If 0 that is, The proof is completed. Based on Lemma 2.1,we have thefollowing result,see Figure 1. Theorem 2.1(i)Ifa>1and (ii)Ifa≥1andc>(a+1)bor0 (iii)If0 Figure 1:The graph of functions c= and c=(1+a)b. In this section,we discuss the local asymptotic stability of equilibria,the existence of Hopf bifurcation at(u1,v1),the global asymptotic stability of(u1,v1)and the existence of saddle-node bifurcation at the unique positive equilibrium(u0,v0)for system(2.1). Let and assume that(¯u,¯v)is an equilibrium of system(2.1).Then the Jacobin matrix of system(2.1)at the equilibrium(¯u,¯v)is It is obvious that J(0,0)has two real characteristic roots−r<0 and b>0.Hence,(0,0)is an unstable saddle point. The Jacobin matrix of system(2.1)at the equilibrium(1,0)is It is easy to see that if c>(a+1)b,then(1,0)is a saddle point of system(2.1).If c<(a+1)b,then(1,0)is a stable node of system(2.1).When c=(a+1)b,the boundary equilibrium(1,0)is a saddle-node equilibrium. The Jacobin matrix at the equilibrium(uk,vk)(k=1,2)is Note that the determinant of J(uk,vk)is And the trace of J(uk,vk)is From Lemma 2.2 it is clear that det J(u2,v2)<0.So,if(u2,v2)exists,then it is a saddle point of system(2.1).In addition,det J(u1,v1)>0 and thus we know that the stability of the positive equilibrium(u1,v1)(if it exists)will be determined by the sign of the trace of the matrix J(u1,v1). Let Then the trace of J(u1,v1)has the same signs as T.Thus we know that the stability of the positive equilibrium(u1,v1)(if it exists)of system(2.1)will be determined by the sign of T. 2.2.1 The case c>(a+1)b For convenience,define c0by Proof According to the definition of tr J(u1,v1)and noticing that T(c0)=0,we have Since the result of Lemma 2.4 holds.The proof is completed. According to Lemmas 2.3 and 2.4,it is easy to get the following results. Theorem 2.2(i)Ifa≥andc>(a+1)bor0 (ii)If0 (iii)If0 Table 1:Stability and instability of the equilibrium(u1,v1)of(2.1)in(a,b,c)space 2.2.2 The case0 Similarly,define c1by when 0 In terms of Lemmas 2.5 and 2.6,we can obtain the following results. Table 2:Stability of the equilibrium(u1,v1)of(2.1)in the parameter(a,b,c)space In the following,according to Theorem 2.2 in[11],we state a global asymptotic stability result of the unique positive equilibrium(u1,v1)of system(2.1). Theorem 2.4then system(2.1)possesses a global asymptotic stable positive equilibrium(u1,v1). We end this section by stating a conclusion regarding the saddle-node bifurcation of coexistence equilibria of system(2.1).According to the above analysis,we know thatsystem(2.1)has a unique positive equilibrium(u0,v0)as 0 It is easy to see that J(u0,v0)has a zero eigenvalue andthe other one is r(1−).According to Sotomayor’s theorem[4,10],when r(1 −)<0,that is, Theorem 2.5If In this section,we are concerned with the effect of diffusion coefficients d1and d2on the stability of positive constant steady state solutions(uk,vk)(k=1,2)of the reaction-diffusion system(1.6). Define a real-valued Sobolev space X by and the complex-valued space XCexpanded by X is defined as The linearized system of system(1.6)at(uk,vk)is where Let the linear operator L(uk,vk)with the domain D(L)=XCbe defined by Then the local asymptotic stability of the positive constant steady state solution(uk,vk)of system(1.6)is determined by the signs of real parts of eigenvalues of the linear operator L(uk,vk).If all the eigenvalues of L(uk,vk)have negative real parts,then the positive constant steady state solution(uk,vk)of system(1.6)is locally asymptotically stable.If the linear operator L(uk,vk)has at least one eigenvalue with positive real part,then(uk,vk)is unstable[6,16,17]. Assume thatλis the eigenvalue of the linear operator L(uk,vk)with the eigenfunction(ϕ,ψ)T.Then λ and(ϕ,ψ)Tsatisfy the following equality It is well known that the eigenvalue problem has the eigenvalues µi(i∈ N0={0,1,2,···})satisfying withµn→∞as n→∞. For j∈N0,define the second matrix Lj(uk,vk)by Lemma 3.1Ifλ∈Cis an eigenvalue of the operatorL(uk,vk),then there exists somen0∈N0such thatλis the eigenvalue ofLn0(uk,vk)and vice versa. ProofUse E(µi)to denote the eigenspace corresponding to µiin W1,2(Ω).Letbe an orthonormal basis of E(µi)and the space spanned by ϕijis represented by Xij.Then Let Then According to the above decomposition,the eigenfunction(ϕ,ψ)T∈XCof L(uk,vk)corresponding to the eigenvalueλcan be decomposed as Therefore,(3.2)can be rewritten as From the orthogonality of the function sequenceone can get from(3.5)that for all n ∈ N0and j=1,···,dim Eµn, Since(ϕ,ψ)∈ XCis the eigenfunction of L(uk,vk)corresponding to the eigenvalue λ and(ϕ,ψ)/=0,there must exist some n0∈ N0such that 0 /=(an0j,bn0j)∈ C × C.Therefore,λis the eigenvalue of the matrix Ln0(uk,vk). Ifλis the eigenvalue of some matrix Ln0(uk,vk),then there exists a nonzero vector(an0,bn0)∈C×C such that(3.5)holds.Let Then(ϕ,ψ) /=0 and This demonstrates thatλis an eigenvalue of L(uk,vk)and thus the proof is complete. Remark 3.1Lemma 3.1 shows that if for all j∈N0,the eigenvalues of Lj(uk,vk)have negative real parts,then the positive constant steady state solution(uk,vk)of system(1.6)is locally asymptotically stable and is unstable if there exists a certain n0∈N0such that Ln0(uk,vk)has at least one eigenvalue with positive real part. From the discussions in Section 2,we know that L0(u2,v2)has two real eigenvalues with the opposite signs and thus it follows the following result: Theorem 3.1Assume that0positive constant steady state(u2,v2)of system(1.6)is unstable. In what follows,we analyze the local asymptotic stability of positive constant steady state(u1,v1)of system(1.6).Let and If<0,that is,the positive equilibrium(u1,v1)of system(2.1)is locally asymptotically stable,then for all j∈N0,Tj(u1,v1)<0 and Dj(u1,v1)>0.It follows that all the eigenvalues of Lj(u1,v1)(j∈N0)have negative real parts which implies that all the eigenvalues of the operator L(u1,v1)have negative real parts.Therefore,the positive constant steady state solution(u1,v1)of system(1.6)is locally asymptotically stable.If>0,that is,the positive equilibrium(u1,v1)of system(2.1)is unstable,then T0(u1,v1)>0 and D0(u1,v1)>0.Thus L0(u1,v1)has at least one eigenvalue with positive realpart and hence the operator L(u1,v1)has at least one eigenvalue with positive real part.Therefore,the positive constant steady state solution(u1,v1)of system(1.6)is unstable. From the analysis in Section 2,we have T0(cH)=0 and D0(cH)>0 where cH=c0or c1.In addition,Tj(cH)<0 and Dj(cH)>0 for any j>0.This shows that when c=cH,L(u1,v1)has a pair of purely imaginary eigenvalues.Therefore,when c varies near cH,L(u1,v1)has a pair of conjugate complex eigenvalues δ(c)±iω(c)withω(c)>0.Meanwhile,it is easy to see that Now we can state the following results. Remark 3.2From Theorems 3.2 and 3.3,we can see that the diffusion coefficients d1and d2have no effect on the stability of positive constant steady state solutions(u1,v1)and(u2,v2). In this section,by using the software package Matlab and the numerical methods to solve the ordinary and partial differential equations,we shall give some numerical simulations in order to verify the theoretical results obtained in Sections 2 and 3. Example 4.1(i)Take r=0.4,a=,b=3 and c=6 in system(2.1).Then c>(1+a)b=.Therefore from(i)in Theorem 2.2 we know that the positive equilibrium E1(0.5,0.2)of system(2.1)is locally asymptotically stable,see Figure 2. (ii)Take r=0.5,a=and b=4 in system(2.1).Then 0 (iii)Take r=0.2,a=and b=5 in system(2.1).Then 0 Example 4.2(i)Take r=0.5,in system(2.1).Then,the positive equilibrium E1(0.7071,0.1709)of system(2.1)is locally asymptotically stable.The positive equilibrium E2(0.9428,0.0445)of system(2.1)is unstable,see Figure 5. Figure 2:Numerical approximations for system(2.1)when a=,b=3,c=6,r=0.4. Figure 3:Numerical approximations for system(2.1)when a=,b=4,c=8,r=0.5. Figure 4:Numerical approximations for system(2.1)when a=,b=5,c=7,r=0.2. Figure 5:Numerical approximations for system(2.1)when a=,b=2,c=,r=0.5. Figure 6:Numerical approximations for system(2.1)when a=,b=6,c=,r=0.1. Figure 7:Numerical approximations for system(2.1)when a=,b=2,c=,r=0.6.There exists a stable periodic solution surrounding the positive equilibrium E1(0.3629,0.1618). Figure 8:Numerical approximations for system(2.1)when a=,b=7,c=7,r=0.7. In this subsection,we shall give some concrete examples and numerical simulations in order to verify the theoretical results obtained in Section 3.To this end,we take Ω as the one-dimensional spatial domain(0,ℓπ)(ℓ>0)and consider the following system Example 4.3(i)Take r=0.4,a=,b=3,c=6 and d1=2,d2=5,ℓ=in system(4.1).Then c>(1+a)b=and from(i)in Theorem 3.2 we know that the constant positive steady state solution E1(0.5,0.2)of system(4.1)is locally asymptotically stable,see Figure 9. (ii)Take r=0.5,a=,b=4,c=8 and d1=3,d2=6,ℓ=in system(4.1).Then by(i)of Theorem 3.2 one can get that the positive steady state solution E1(0.1340,0.1160)of system(4.1)is locally asymptotically stable for all c>c0=,see Figure 10. (iii)Take r=0.2,a=,b=5,c=7 and d1=4,d2=8,ℓ=2 in system(4.1).Based on(ii)of Theorem 3.2,we know that when 6=(a+1)b Figure 9:Numerical approximations for(4.1)when a=,b=3,c=6,r=0.4,d1=2,d2=5,ℓ=0.5 as well as initial value u0(x)=0.5+0.01 cos(2x)and v0(x)=0.2−0.01 cos(2x)for x∈ [0,0.5π]. Figure 10:Numerical approximations for(4.1)when a=,b=4,c=8,r=0.5,d1=3,d2=6,ℓ= as well as initial value u0(x)=0.134+0.001 cos(2x)and v0(x)=0.116−0.001 cos(2x)for x∈[0,1.5π]. Figure 11:Numerical approximations for(4.1)when a=,b=5,c=7,r=0.2,d1=4,d2=8,ℓ=2 as well as initial value u0(x)=0.161+0.001 cos(2x)and v0(x)=0.037−0.001 cos(2x)for x∈ [0,2π]. Figure 12:Numerical approximations for(4.1)when a=,b=2,c=,r=0.5,d1=1,d2=9,ℓ=1 as well as initial value u0(x)=0.70+0.01 cos(2x)and v0(x)=0.17−0.01 cos(2x)for x∈ [0,π]. Figure 13:Numerical approximations for(4.1)when a=,b=2,c=,r=0.5,d1=1,d=9,ℓ=1 as well as initial value u(x)=0.94+0.01 cos(2x)and v(x)=200 0.04−0.01 cos(2x)for x∈ [0,π]. Figure 14:Numerical approximations for(4.1)when a=,b=6,c=,r=0.1,d1=5,d2=7,ℓ=3 as well as initial value u0(x)=0.500+0.001 cos(2x)and v0(x)=0.027−0.001 cos(2x)for x∈ [0,3π]. Figure 15:Numerical approximations for(4.1)when a=,b=6,c=,r=0.1,d1=5,d2=7,ℓ=3 as well as initial value u0(x)=0.583+0.001 cos(2x)and v0(x)=0.026−0.001 cos(2x)for x∈ [0,3π]. Figure 16:Numerical approximations for(4.1)when a=,b=2,c=,r=0.6,d1=8,d2=13,ℓ=4 as well as initial value u0(x)=0.36+0.01 cos(2x)and v0(x)=0.16−0.01 cos(2x)for x∈[0,4π]. Figure 17:Numerical approximations for(4.1)when a=,b=2,c=,r=0.6,d1=8,d2=13,ℓ=4 as well as initial value u0(x)=0.80+0.01 cos(2x)and v0(x)=0.11−0.01 cos(2x)for x∈ [0,4π]. Figure18:Numerical approximations for(4.1)when a=,b=7,c=7,r=0.7,d1=10,d2=15,ℓ=5 as well as initial value u0(x)=0.21+0.01 cos(2x)and v0(x)=0.11−0.01 cos(2x)for x∈[0,5π]. Figure 19:Numerical approximations for(4.1)when a=,b=7,c=7,r=0.7,d1=10,d2=15,ℓ=5as well as initial value u0(x)=0.78+0.01 cos(2x)and v0(x)=0.11−0.01 cos(2x)for x∈[0,5π]. [1]J.F.Andrews,A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates,Biotechnol.Bioeng,10(1968),707-723. [2]A.A.Andornov,E.A.Leontovich,I.I.Gordon and A.G.Maier,Theory of Bifurcations of Dynamic Systems on A Plane,Israel Program for Scientific Translations,Jerusalem,1971. [3]H.I.Freedman and G.S.K.Wolkowicz,Predator-prey systems with group defence:The paradox of enrichment revisited,Bull.Math.Biol.,48(1986),493-508. [4]M.Haque,Ratio-dependent predator-prey models of interacting populations,Bull.Math.Biol.,71(2009),430-452. [5]A.J.Lotka,Elements of Physical Biology,New York:Williams and Wilkins,1925. [6]X.Li and W.H.Jiang,Hopf bifurcation and turing instability in the reaction diffusion Holling-Tanner predator-prey model,Ima Journal of Applied Mathematics,78(2013),287-306. [7]X.B.Lin,Exponential dichotomy and stability of long periodic solutions in predatorprey models with diffusion,in Partial Differential Equations,J.Wiener and J.K.Hale,eds.,Longman Scientific and Technical,Harlow,UK,1992,101-105. [8]K.Mischaikow and G.S.K.Wolkowicz,A predator-prey system involving group defense:A connection matrix approach,Nonlinear Anal.,14(1990),955-969. [9]Y.H.Pang and M.X.Wang,Non-constant positive steady states of a predator-prey system with non-monotonic functional response and diffusion,London Math.Soc,88:3(2004),135-157. [10]L.Perko,Differential Equations and Dynamical Systems,Springer,New York,1996. [11]S.G.Ruan and D.M.Xiao,Global analysis in a predator-prey system with nonmonotonic functional response,Siam J.Appl.Math.,61:4(2001),1445-1472. [12]W.Sokol and J.A.Howell,Kinetics of phenol oxidation by washed cells,Biotechnol.Bioeng,23(1980),2039-2049. [13]V.Volterra,Variazionie fluttuazionidelnumero d’individuiin specie animaliconviventi,Mem.Acad.Licei.,2(1926),31-113. [14]G.S.K.Wolkowicz,Bifurcation analysis of a predator-prey system involving group defence,Siam J.Appl.Math.,48(1988),592-606. [15]S.Wiggins,Introduction to Applied Nonlinear Dynamical Systems and Chaos,Springer,New York,1991. [16]F.Q.Yi,J.J.Wei and J.P.Shi,Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system,J.Differential Equations,246(2009),1944-1977. [17]F.Q.Yi,Bifurcation theory and its applications in semilinear partial differential equation,unpublished PhD dissertation,Harbin Institute of Technology,pp.11-81,2008.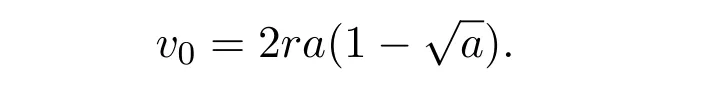
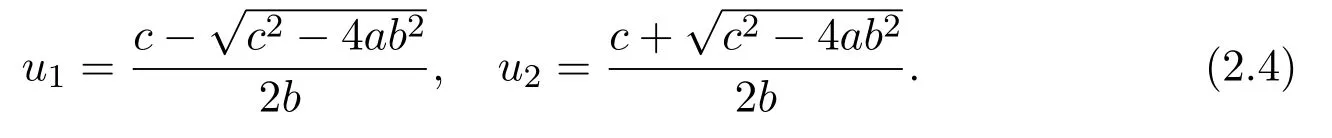
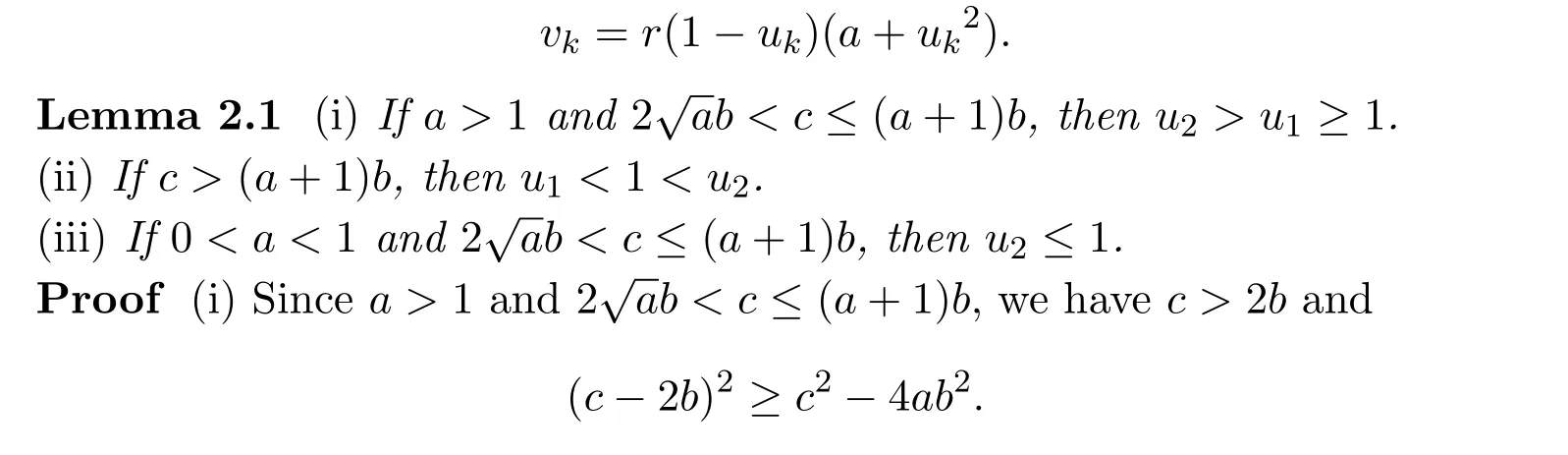

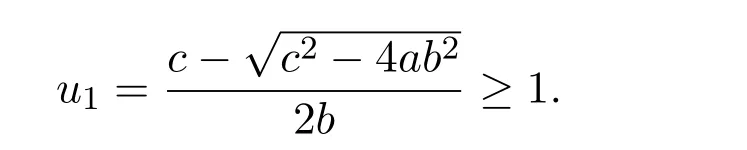
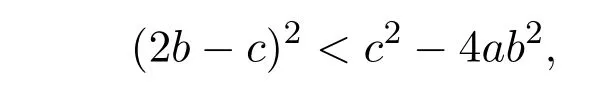
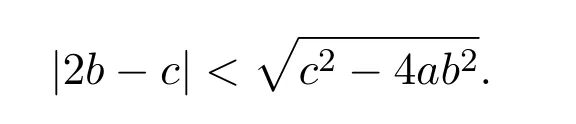
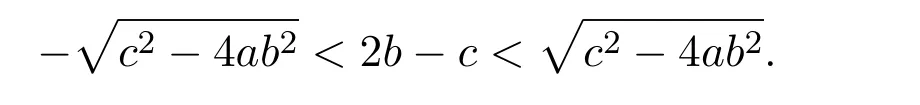

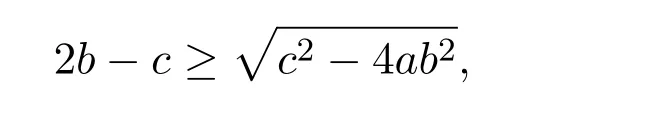
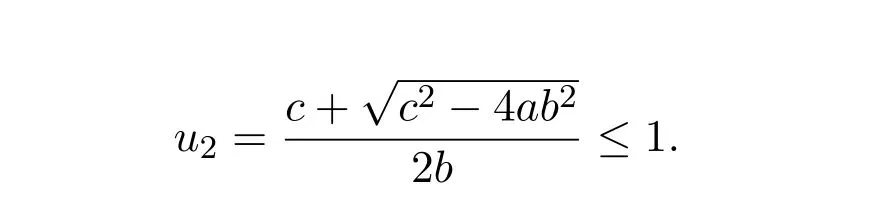

2.2 Stability of equilibria and bifurcation
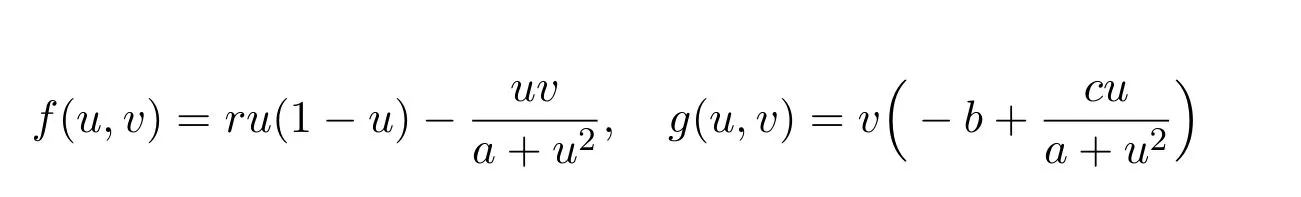
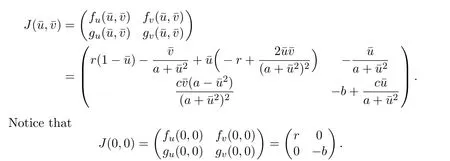
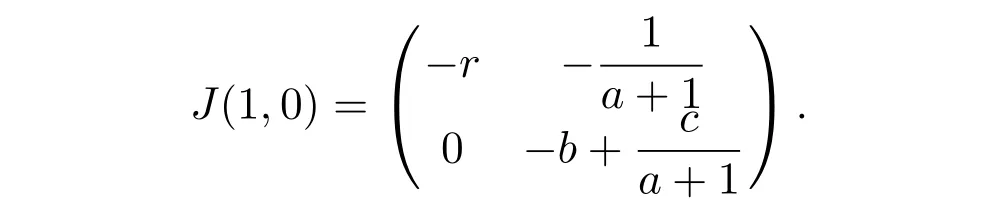
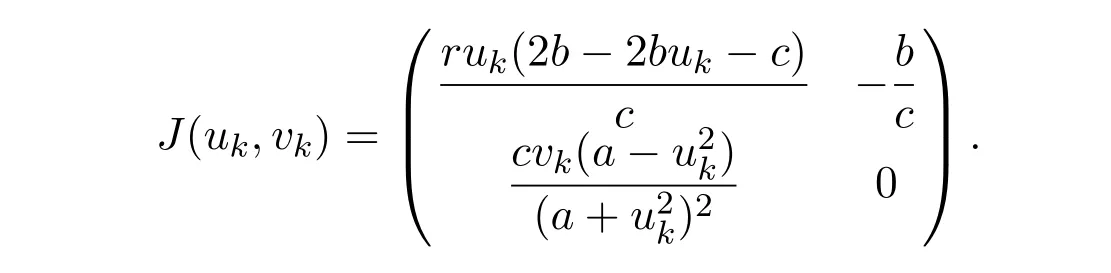
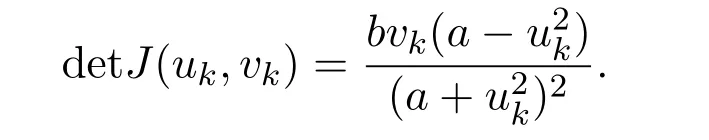
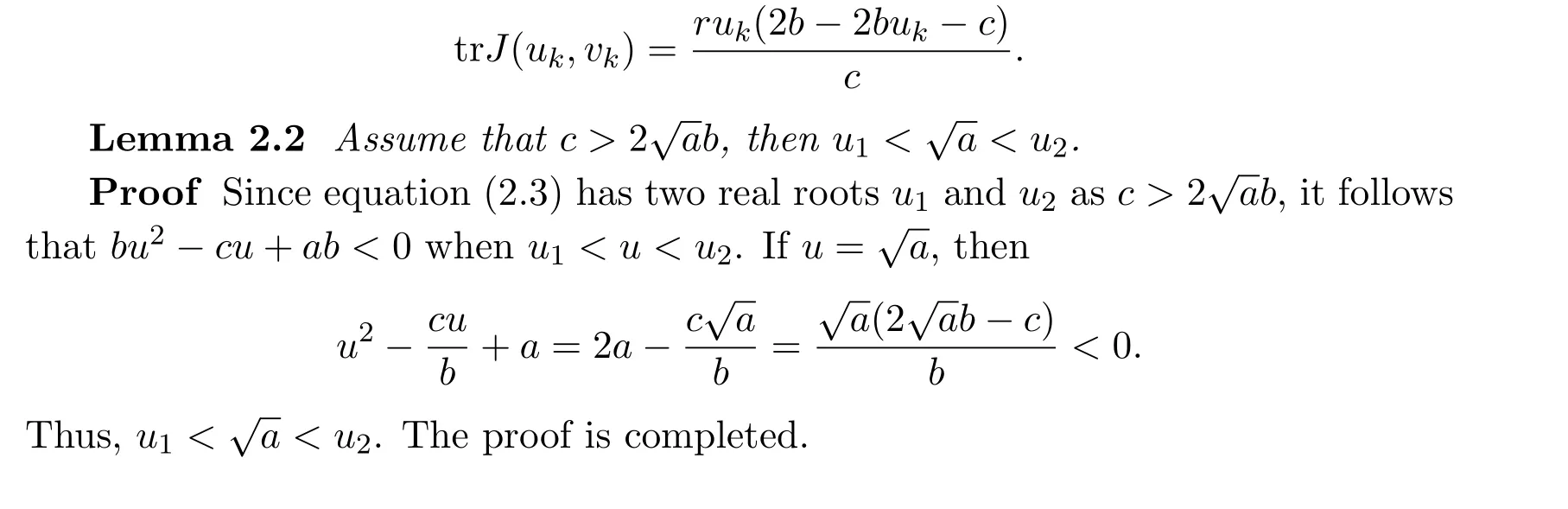
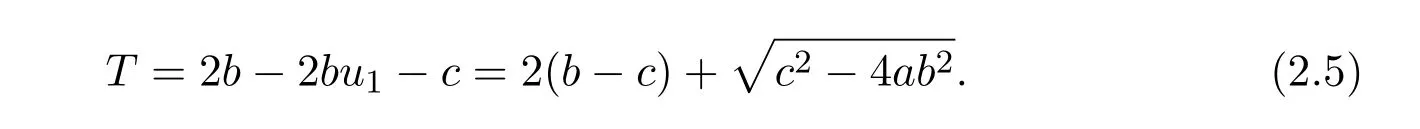
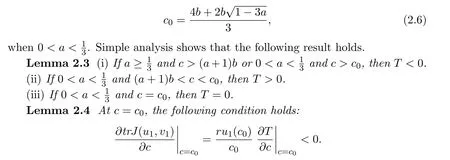

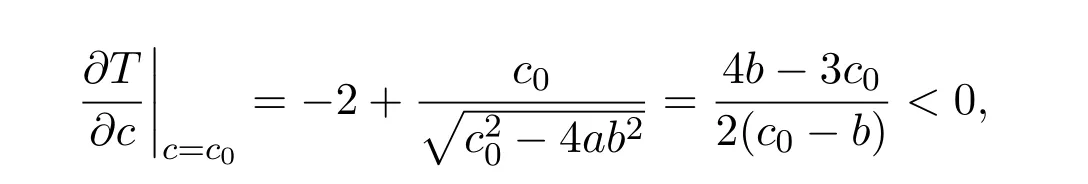


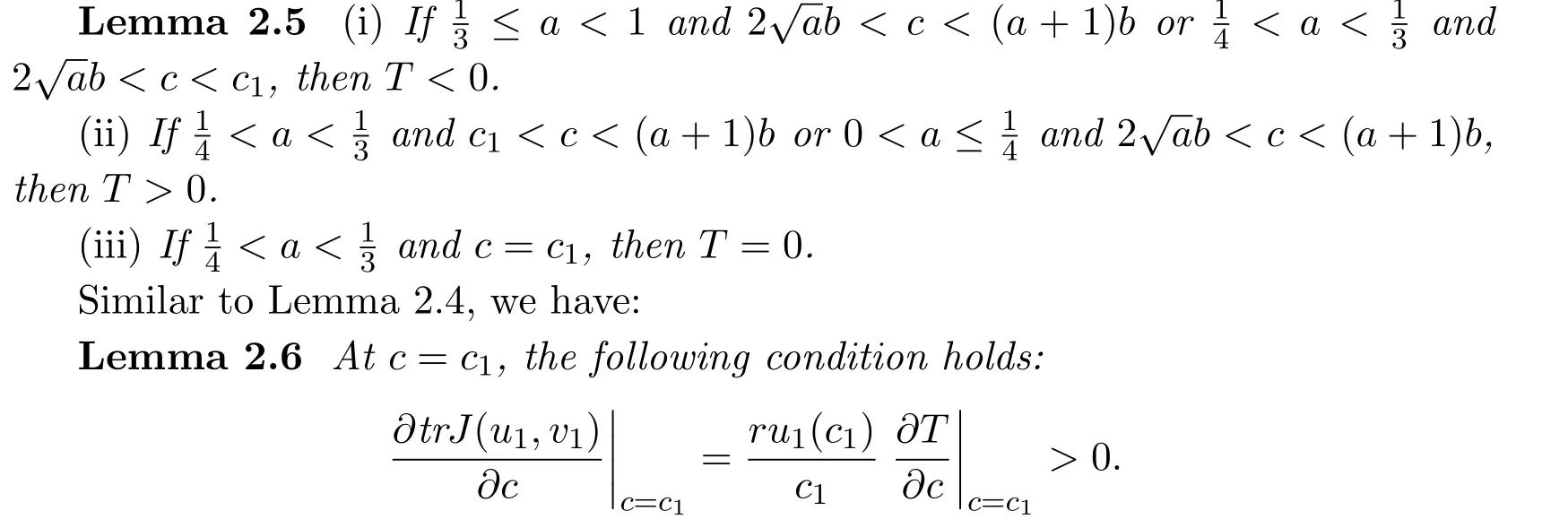


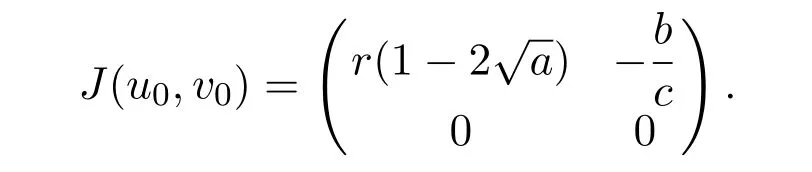
3 The Effect of Diffusion on Stability of Positive Equilibria
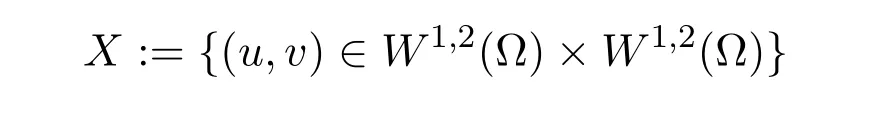

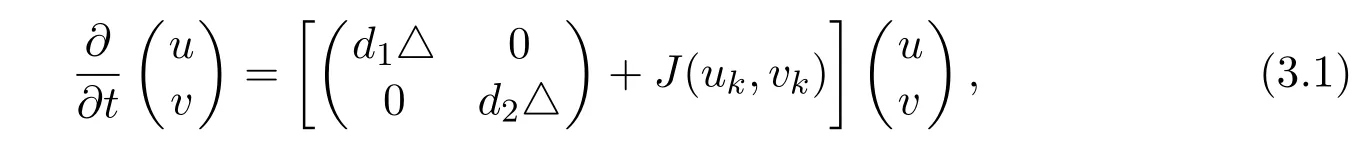
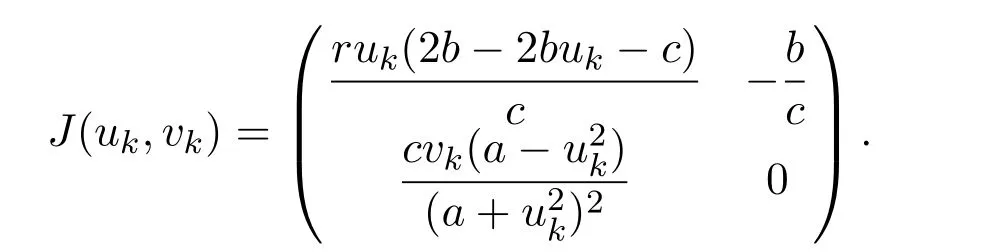
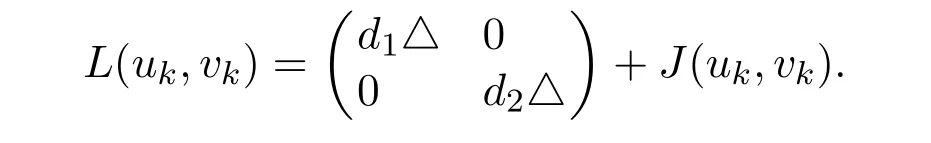
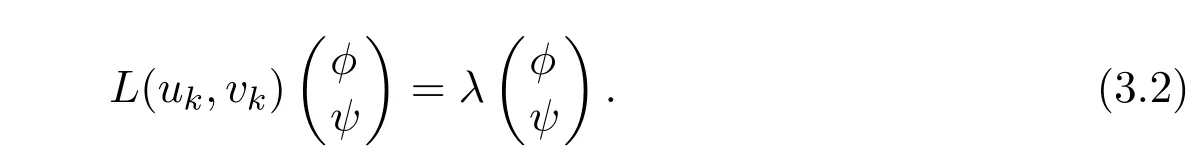

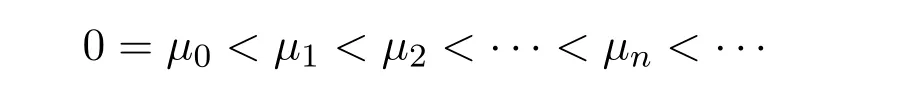
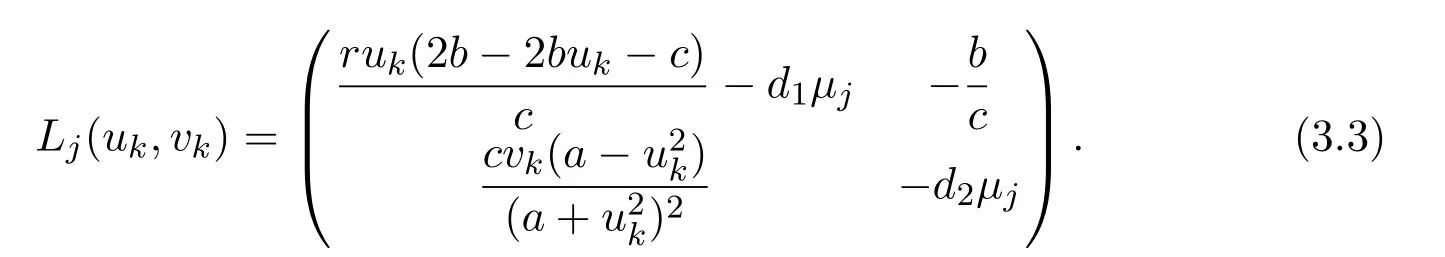

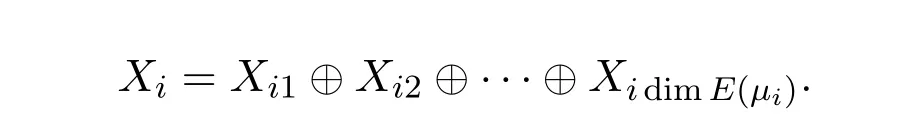
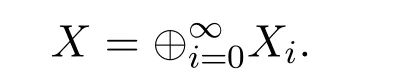
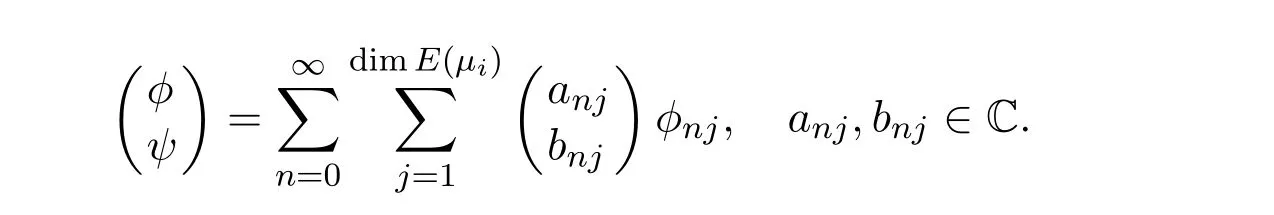
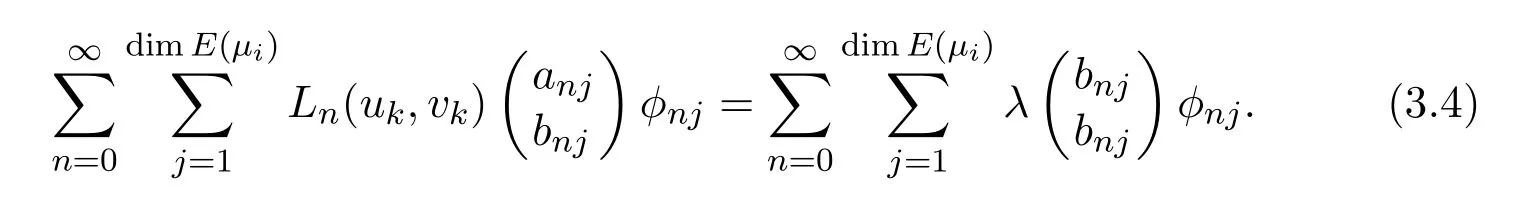
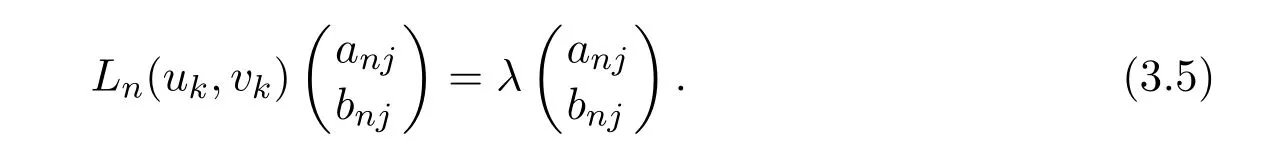
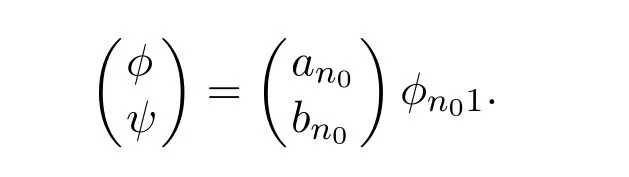
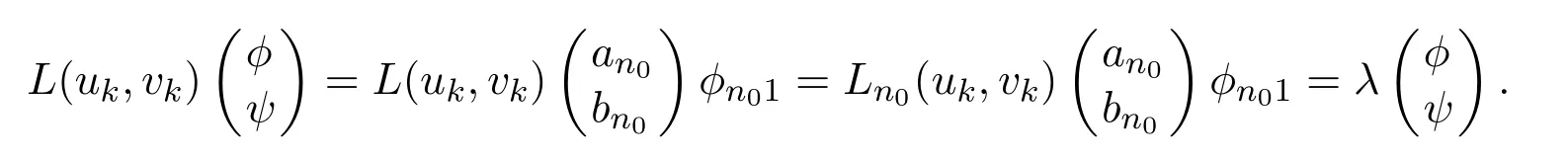

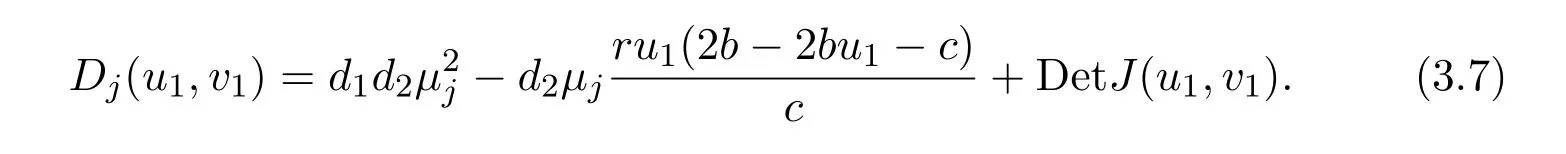
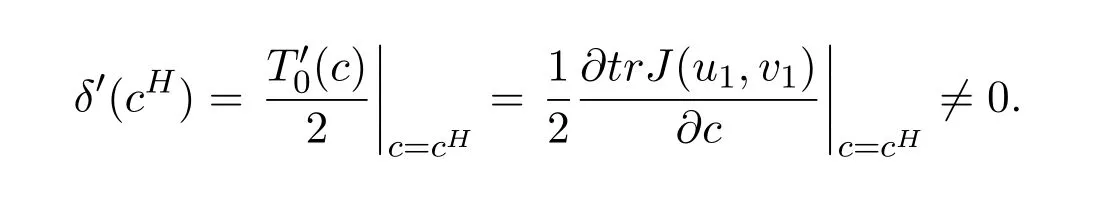

4 Examples and Numerical Simulations
4.1 Examples and numerical simulations of system(2.1)


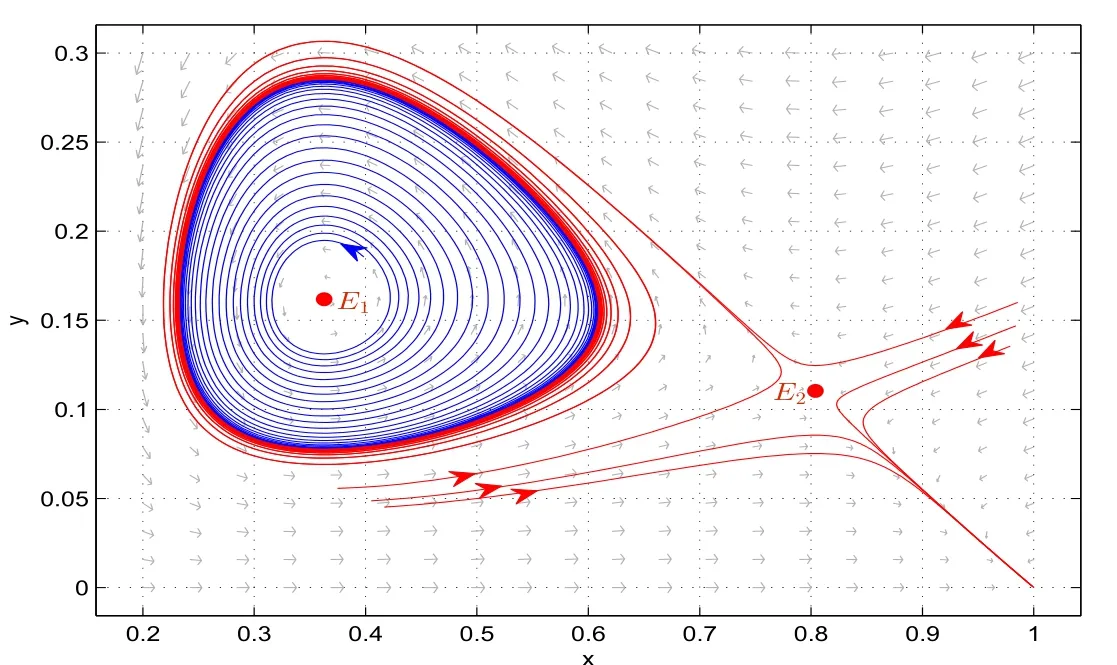
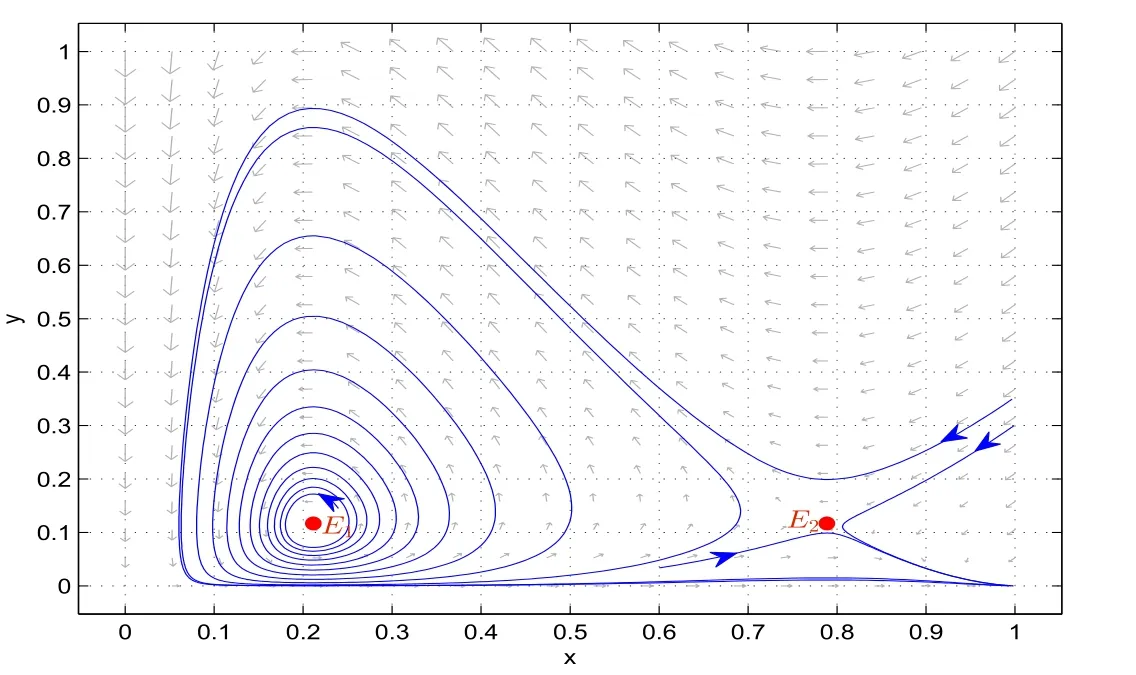
4.2 Examples and numerical simulations of system(1.6)
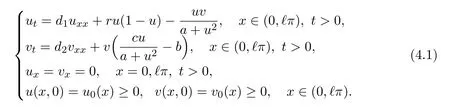
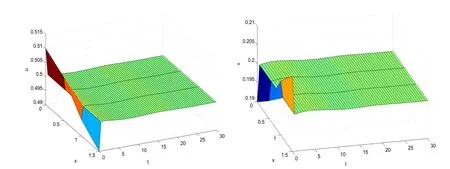




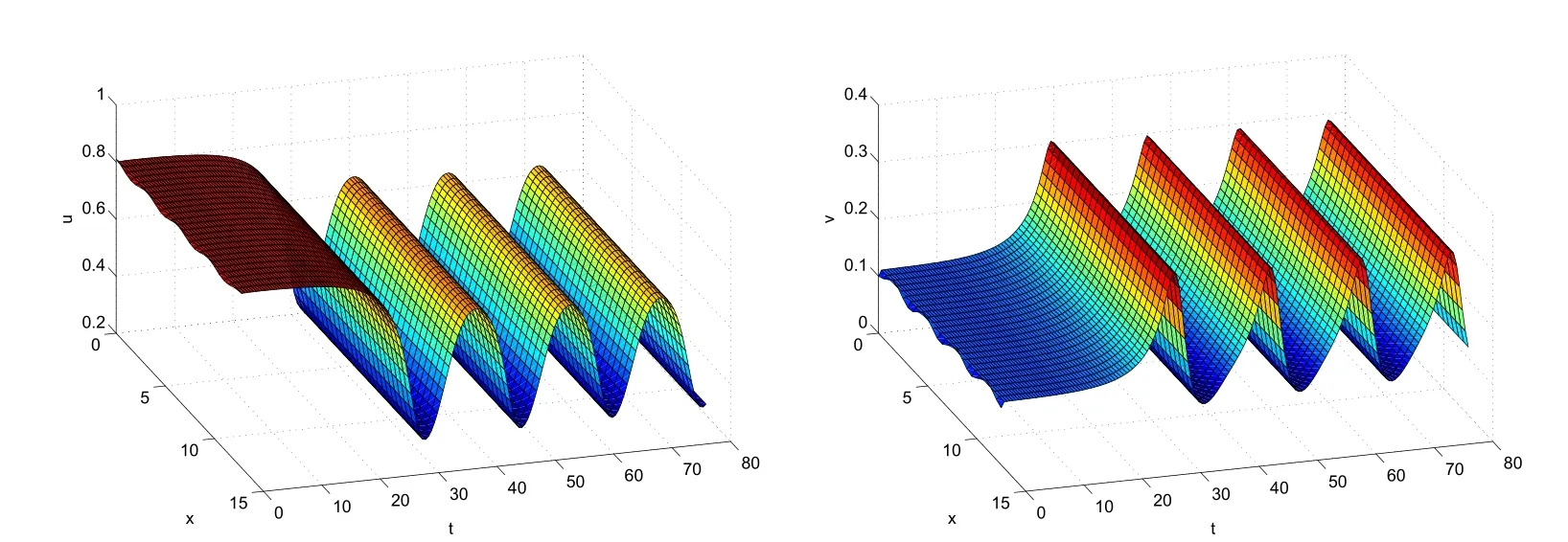

杂志排行
Annals of Applied Mathematics的其它文章
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
- THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
- NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
- A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
- A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
