A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
2018-07-06YuLiuXinyuGuan
Yu Liu,Xinyu Guan
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
1 Introduction
During the last decade,many scholars have focused on the study of the commensal symbiosis model[1-12],which describes a relationship only favorable to the one side and has no influence to the other side.
Sun and Wei[4]first proposed a intraspecific commensal model:
They investigated the local stability of all equilibrium points.However,they did not give any information about the global dynamic behaviors of the system.Zhu,Xu and Li[11]proposed a commensalism model,in which one of the species could not be survived independently.By giving the phase trajectories analysis of the system,they are able to analyse the stability property ofallthe equilibria of the system.Han and Chen[5]incorporated the feedback control variables into the commensal symbiosis modelsystem(1.1).By constructing some suitable Lyapunov function,they showed that the system admits a unique globally stable positive equilibrium;Xie et al.[6],Xue et al.[13,15]studied the dynamic behaviors of the discrete commensalsymbiosis model;Miao et al.[16]further studied the dynamic behaviors of the periodic Lotka-Volterra commensal symbiosis model with impulse.
One could see that all of the above systems are based on the traditional Lotka-Volterra model,which made the assumption that the influence of the second species to the first one is linearize.This may not be suitable.Recently,Wu,Liand Zhou[1]further assumed that the relationship between two species is of Holling type functional response,and they established the following two species commensalsymbiosis model
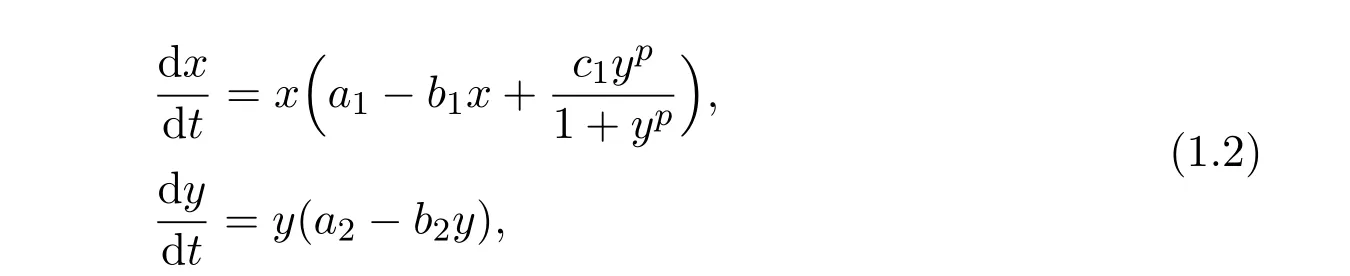
where ai,bi,i=1,2,p and c1are all positive constants with p≥1.By applying the Dulac criterion,they showed that the unique positive equilibrium of the system is globally asymptotically stable.
It brings to our attention that all of the above study did not consider the influence of harvesting.Indeed,to obtain the resource for the development of the human being,harvesting of the species is necessary.Stimulated by the works of Chakraborty,Das and Kar[13],we further incorporated the non-selective harvesting term into system(1.2),and this leads to the following system
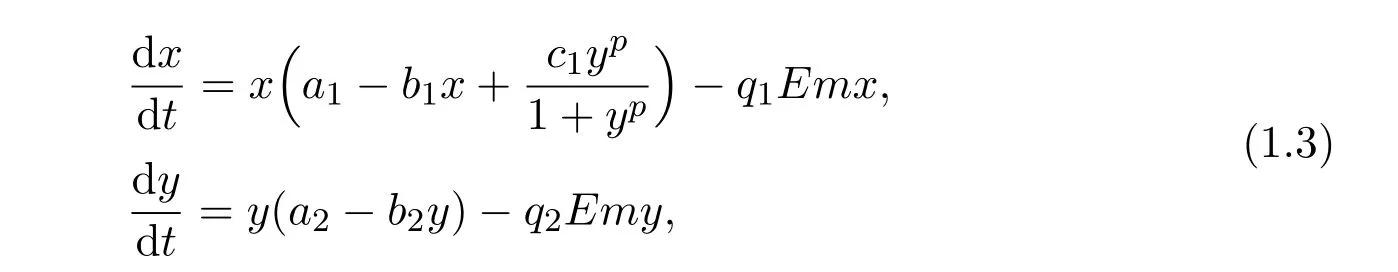
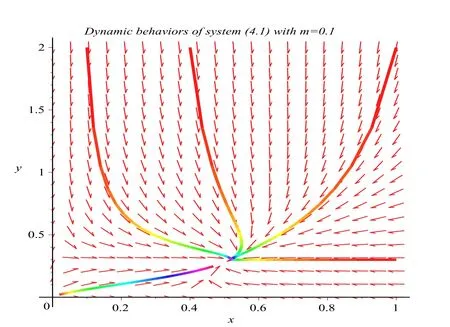
where ai,bi,qi,i=1,2,p,E and c1are all positive constants with p≥1 and E being the combined fishing effort used to harvest,and m(0 The aim of this paper is to investigate the local and global stability property of the possible equilibria of system(1.3).We arrange the paper as follows:In the next section,we will investigate the existence and local stability property of the equilibria of system(1.1).In Section 3,we will investigate the global stability property of the equilibria;in Section 4,an example together with its numeric simulation is presented to show the feasibility of our main results. The equilibria of system(1.3)is determined by equations The system always admits the boundary equilibriums where Obviously,if a1>E mq1,then A2is nonnegative,and if a2>E mq2,then A3is nonnegative.To ensure the positivity of A4,one needs to assume that a1+ Concerned with the local stability property of the above four equilibria,we have the following theorem. Theorem 2.1 (4)assume that and hold,thenA4(x∗,y∗)is locally asymptotically stable. ProofThe Jacobian matrix of system(1.3)is calculated as Then the Jacobian matrix of system(1.3)about the equilibriums respectively.One could easily see that under the assumption of Theorem 2.1,all of the above three matrix have two negative eigenvalues,which means that are all locally asymptotically stable. Note that A4(x∗,y∗)satisfies the equations The Jacobian matrix about the equilibrium A4is given by The eigenvalues of the above matrix areλ1= −b1x∗<0,λ2= −b2y∗<0.Hence,A4(x∗,y∗)is locally stable. This ends the proof of Theorem 2.1. In this section,we try to obtain some sufficient conditions which could ensure the globalasymptotical stability of the equilibria. As a direct corollary of Lemma 2.2 of F.D.Chen[14],we have the following lemma. Lemma 3.1Ifa>0,b>0and≥x(b−ax),whent≥0andx(0)>0,we have Ifa>0,b>0and≤x(b−ax),whent≥0andx(0)>0,we have Lemma 3.2[15]System has a unique globally attractive positive equilibriumy∗= Theorem 3.1 Proof(1)From a1 From the second equation of(1.3)we have Hence For the aboveε>0,there exists a T1>0,such that For t>T1,from the first equation of system(1.3),we have Hence (2)Similarly to the analysis of(1),for arbitrary enough smallε>0,there exists a T2>0,such that For t>T2,from the first equation of system(1.3),we have It follows from Lemma 3.1 that On the other hand,from the first equation of system(1.3),we also have It follows from Lemma 3.1 that It follows from(3.7)and(3.8)that Sinceεis any arbitrary small positive constant,setting ε→0 in the above inequality leads to (3)Consider the function noting that Hence,f(x)is a monotonic function of x.Forε>0 enough small,without loss of generality,we may assume thatε<.From(3.3)and the monotonic increasing of the function From the second equation of(1.3)we have It follows from Lemma 3.2 that Forε>0 enough small,there exists an enough large T3>0,such that For t>T3,from the first equation of system(1.3),(3.9)and(3.10),we have Hence (4)Similarly to the analysis of(3),from the second equation of system(1.3)and Lemma 3.1,we have Hence,for arbitrary small positive constantε>0(without loss of generality,we may assume thatε For t>T4,from the first equation of system(1.3)and(3.11),we have It follows from Lemma 3.1 and the monotonic of the function f(x)that For t>T4,from the first equation of system(1.3)and(3.11),we also have It follows from Lemma 3.1 and the monotonic of the function f(x)that (3.12)together with(3.13)shows that Settingε→0 in(3.14)leads to Consequently,A4(x∗,y∗)is globally attractive. This completes the proof of Theorem 3.1. Now let us consider the following example. Example 4.1Consider the following system In this system,corresponding to system(1.3),we take a1=a2=c1=1,b1=b2=2,E=4,q1=0.5,q2=1.For the system without harvesting,that is,m=0,from Wu,Li and Zhou[1],the system admits a unique positive equilibriumwhich is globally asymptotically stable. (1)Take m=0.6,then and so,from Theorem 3.1(1),A1(0,0)is globally attractive,see Figure 1; (2)take m=0.3,then holds.From Theorem 3.1(2),A2(0.2,0)is globally attractive,see Figure 2; (3)take m=0.1,then and hold.From Theorem 3.1(4),A4(0.5153846154,0.3)is globally attractive,see Figure 3. Figure 1:Numeric simulations of system(4.1)with m=0.6 and the initial conditions(x(0),y(0))=(0.4,2),(1,0.3),(0.02,0.02),(1,2)and(0.1,2),respectively. Figure 2:Numeric simulations of system(4.1)with m=0.5 and the initial conditions(x(0),y(0))=(0.4,2),(1,0.3),(0.2,0.2),(1,2)and(0.1,2),respectively. Figure 3:Numeric simulations of system(4.1)with m=0.1 and the initial conditions(x(0),y(0))=(0.4,2),(1,0.3),(0.2,0.2),(1,2)and(0.1,2),respectively. A commensal symbiosis model with Holling type functional response and nonselective harvesting in a partial closure is proposed and studied in this paper.Already,Wu,Li and Zhou[1]showed that for the system without harvesting(that is,m=0),the system could admits a unique positive equilibrium,which means that the two species could be coexist in a stable state.However,our results shows that depending on the choice of the parameter m,which represents the fraction of the stock could be permit for harvesting,the system may have four kinds of dynamic behaviors:Extinction,partial survival of the one species,or the coexist of the two species in a stable state.That is,by introducing the harvesting,the dynamic behaviors of the system becomes complicated,and it is weakly in the sense that part or all of the species will be driven to extinction. [1]R.X.Wu,L.Li,X.Y.Zhou,A commensalsymbiosis model with Holling type functional response,Journal of Mathematics and Computer Science,16(2016),364-371. [2]K.Yang,Z.S.Miao,F.D.Chen,X.D.Xie,Influence of single feedback control variable on an autonomous Holling-II type cooperative system,Journal of Mathematical Analysis and Applications,435:1(2016),874-888. [3]F.D.Chen,X.D.Xie,Study on the Dynamic Behaviors of Cooperation Population Modeling,Beijing:Science Press,2014. [4]G.C.Sun,W.L.Wei,The qualitative analysis of commensal symbiosis model of two populations,Mathematical Theory and Application,23:3(2003),64-68. [5]R.Y.Han,F.D.Chen,Globalstability of a commensal symbiosis model with feedback controls,Communications in Mathematical Biology and Neuroscience,Vol.2015(2015),Article ID 15. [6]X.D.Xie,Z.S.Miao,Y.L.Xue,Positive periodic solution of a discrete Lotka-Volterra commensal symbiosis model,Communications in Mathematical Biology and Neuroscience,Vol.2015(2015),Article ID 2. [7]Y.L.Xue,X.D.Xie,F.D.Chen,R.Y.Han,Almost periodic solution of a discrete commensalism system,Discrete Dynamics in Nature and Society,Volume 2015(2015),Article ID 295483,11 pages. [8]Z.S.Miao,X.D.Xie,L.Q.Pu,Dynamic behaviors of a periodic Lotka-Volterra commensal symbiosis model with impulsive,Communications in Mathematical Biology and Neuroscience,Vol.2015(2015),Article ID 3. [9]J.H.Chen,R.X.Wu,A commensal symbiosis model with non-monotonic functional response,Communications in Mathematical Biology and Neuroscience,Vol.2017(2017),Article ID 5. [10]F.D.Chen,L.Q.Pu,L.Y.Yang,Positive periodic solution of a discrete obligate Lotka-Volterra model,Communications in Mathematical Biology and Neuroscience,Vol.2015(2015),Article ID 14. [11]Z.F.Zhu,F.Xu,Y.A.Li,Mathematical analysis on commensalism Lotka-Volterra model of populations,J.Chongqing Inst.Tech.Nat.Sci.Ed.,21:10(2007),59-62. [12]Y.L.Xue,F.D.Chen,X.D.Xie,et al,Dynamic behaviors of a discrete commensalism system,Annals of Applied Mathematics,31:4(2015),452-461. [13]K.Chakraborty,S.Das,T.K.Kar,On non-selective harvesting of a multispecies fishery incorporating partial closure for the populations,Applied Mathematics and Computation,221(2013),581-597. [14]F.D.Chen,On a nonlinear non-autonomous predator-prey model with diffusion and distributed delay,J.Comput.Appl.Math.,180:1(2005),33-49. [15]L.S.Chen,X.Y.Song,Z.Y.Lu,Mathematical Models and Methods in Ecology,Chengdu:Shichuan Science and Technology Press,2002. [16]Y.C.Zhou,Z.Jin,J.L.Qin,Ordinary Differential Equaiton and Its Application,Beijing:Science Press,2003.2 The Existence and Local Stability of the Equilibria
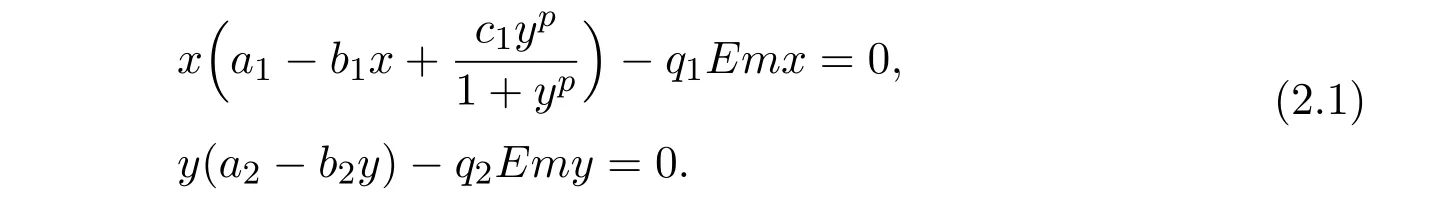
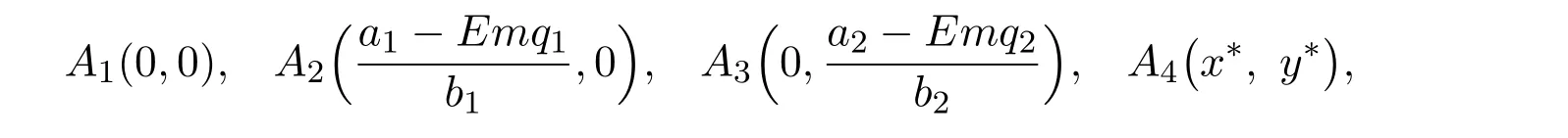
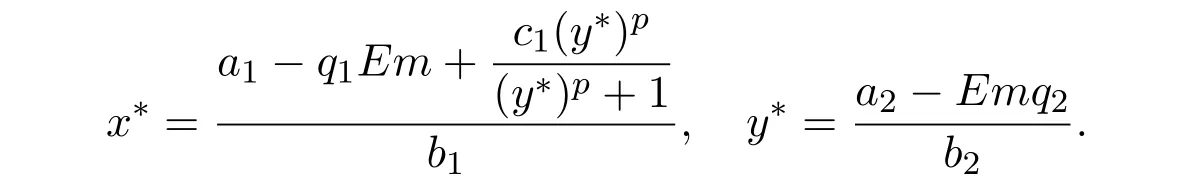
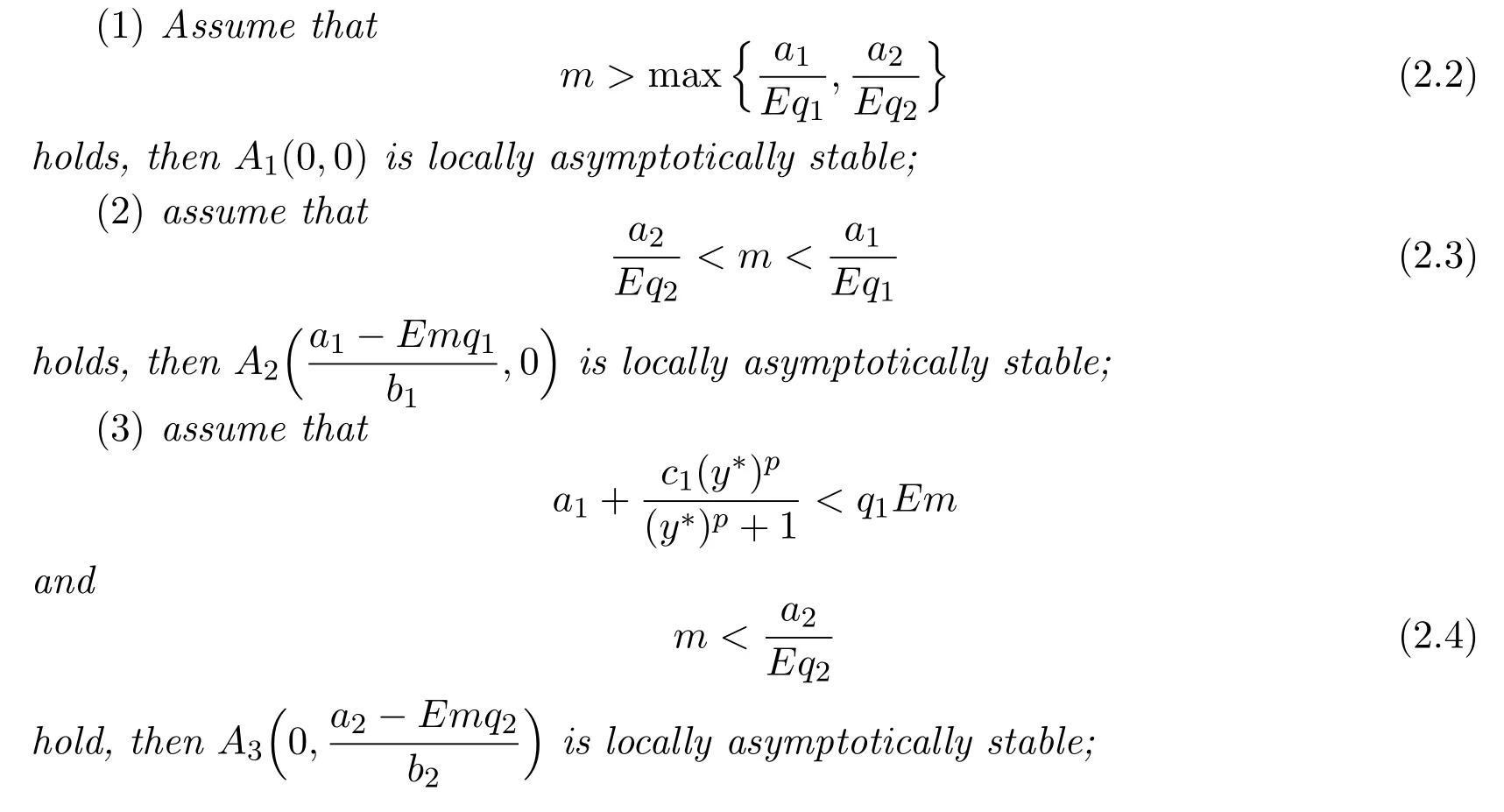


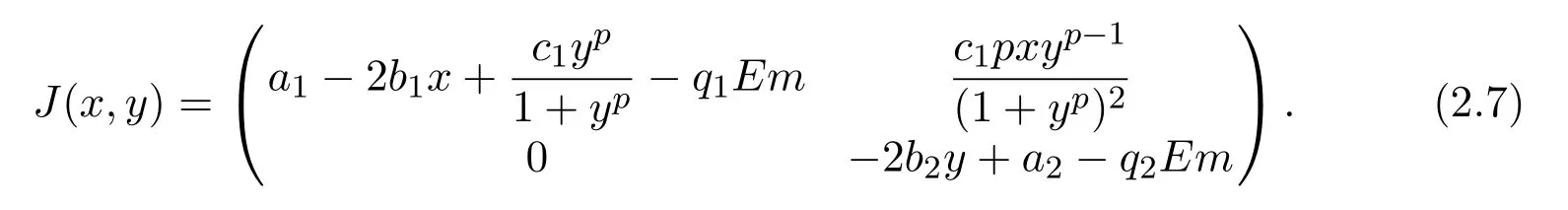

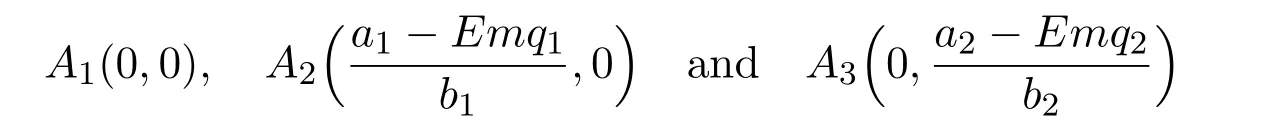

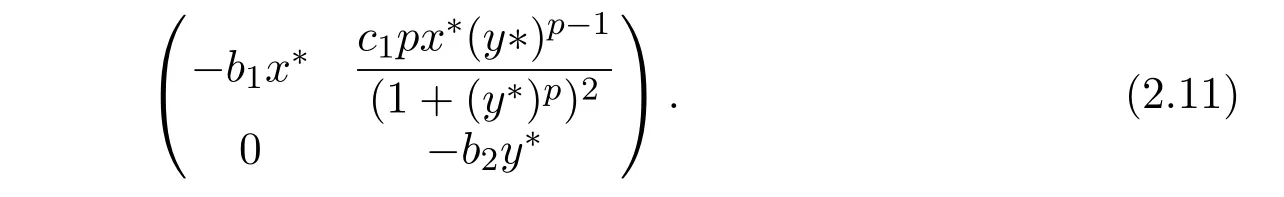
3 Global Stability of the Positive Equilibrium
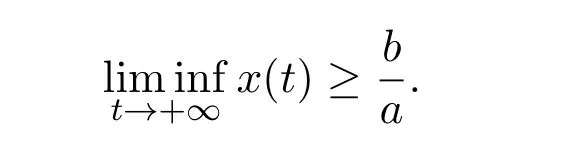

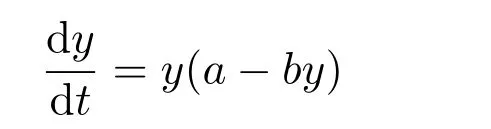

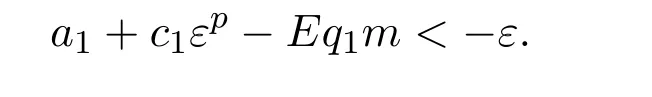
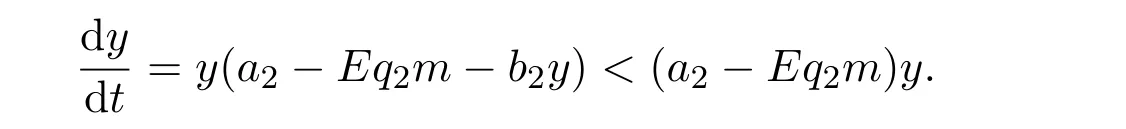
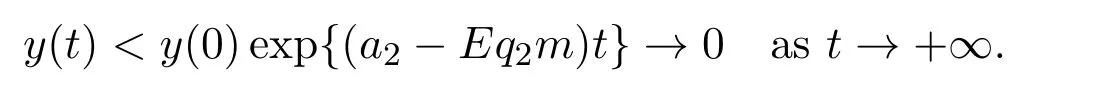
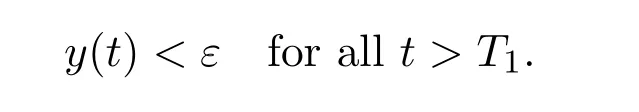
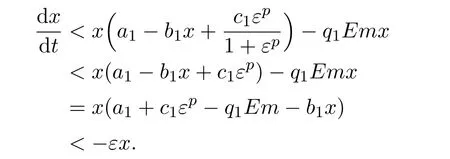
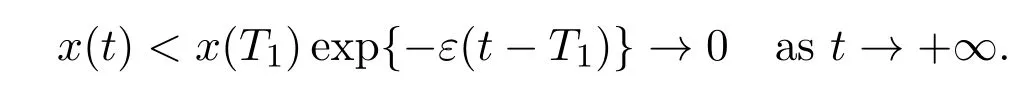
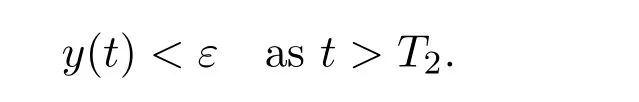
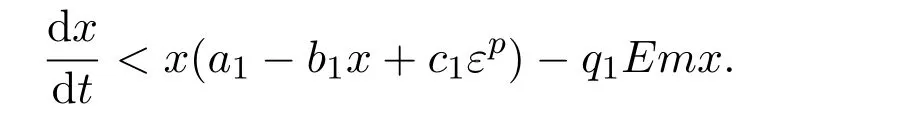
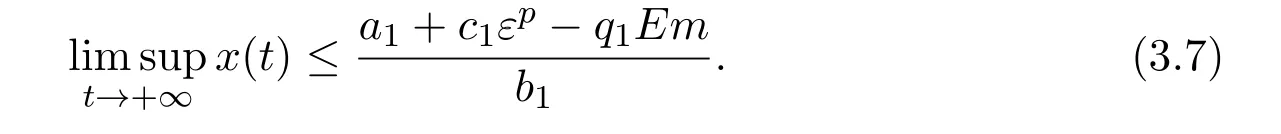
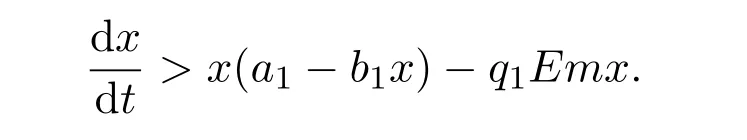

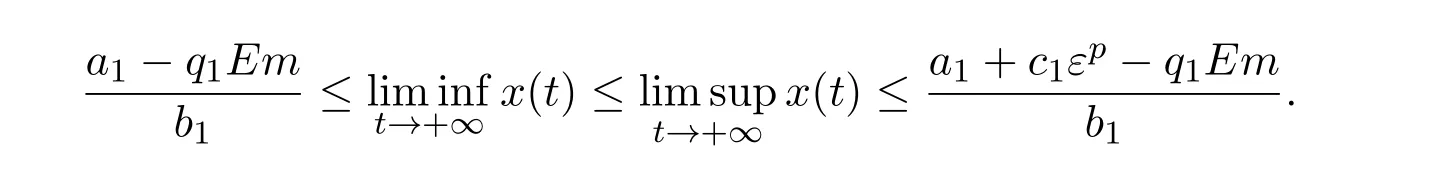
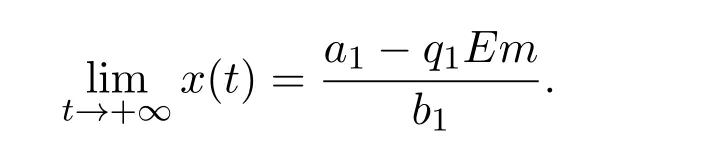
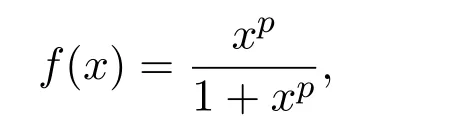
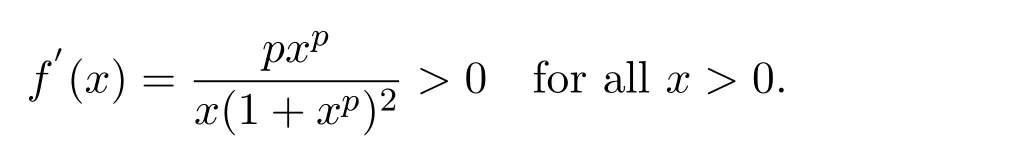

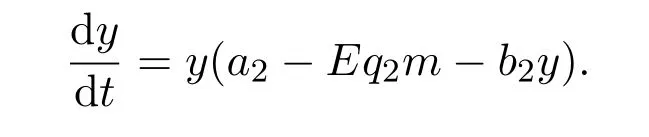
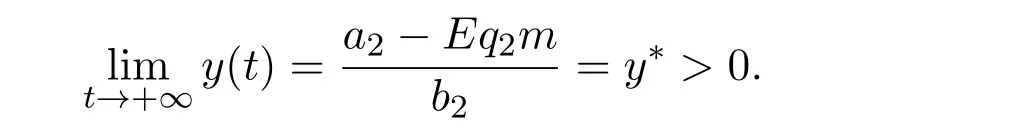
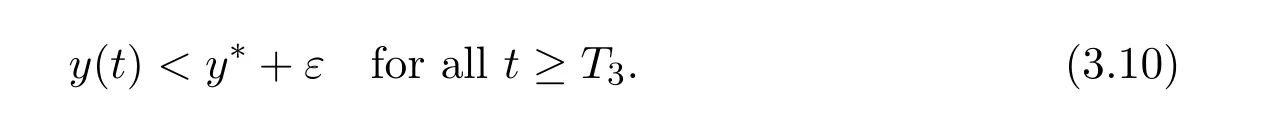
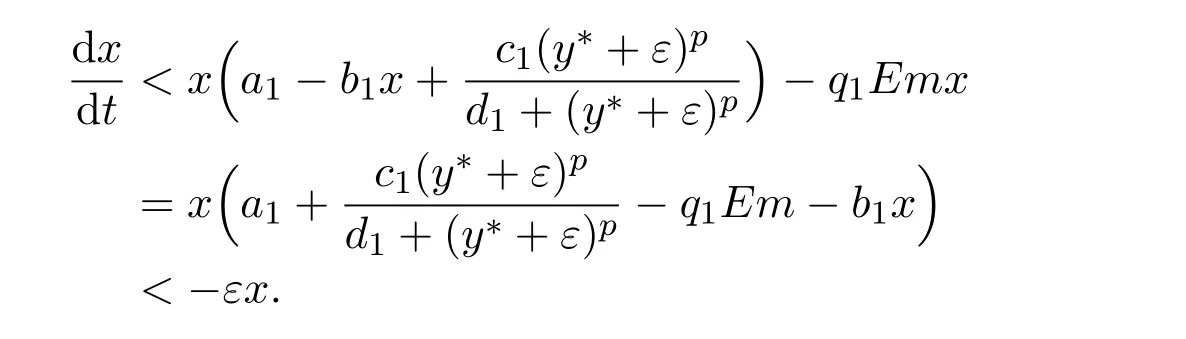
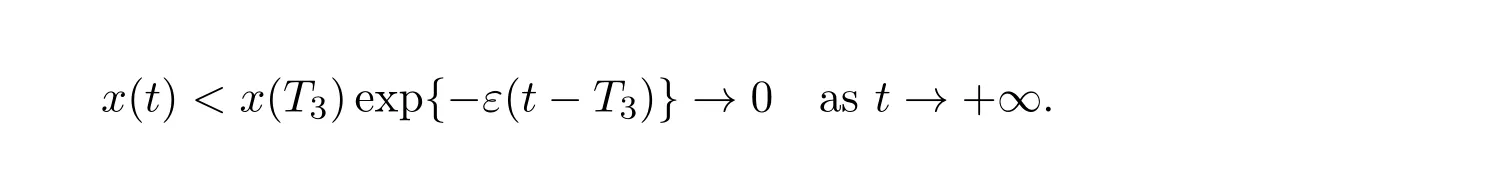

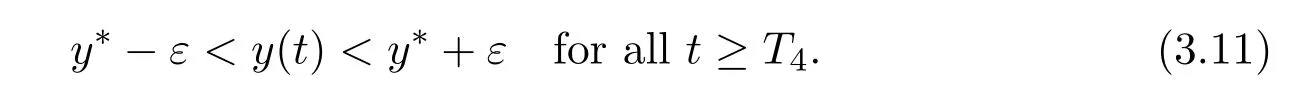
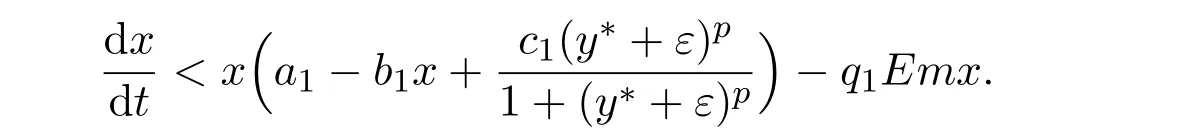
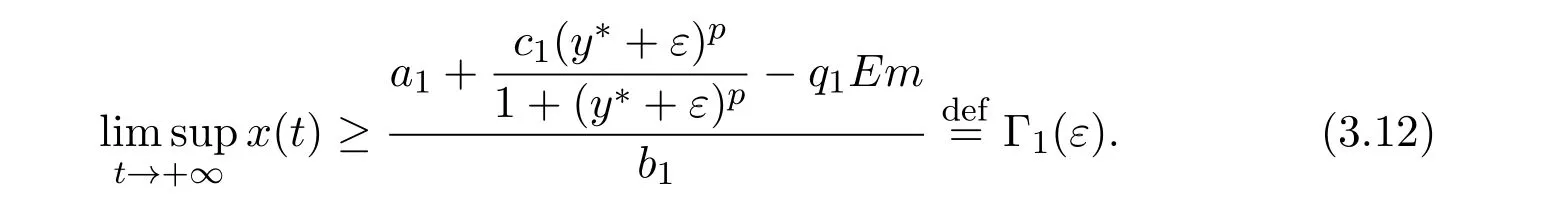
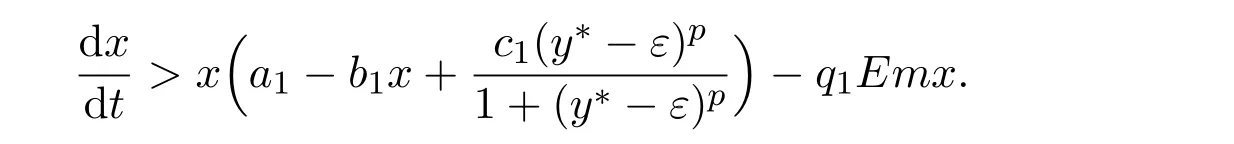

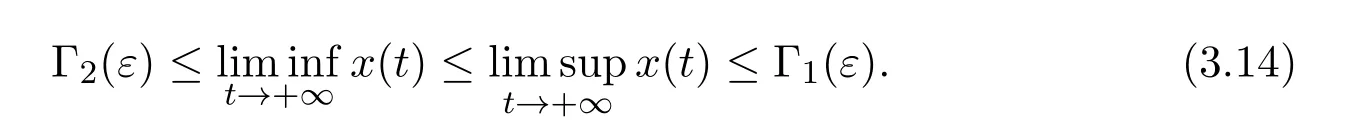
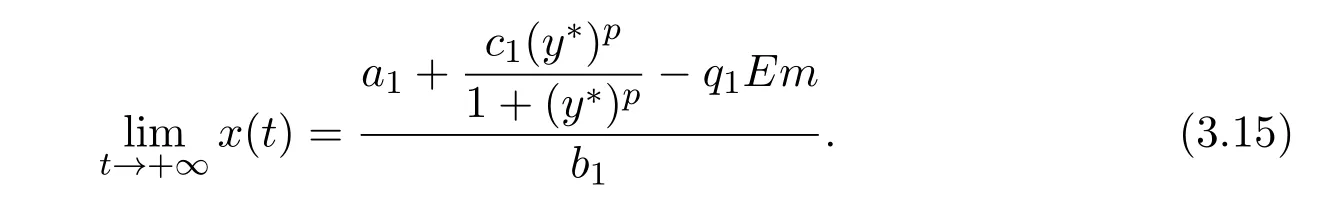
4 Numeric Simulations
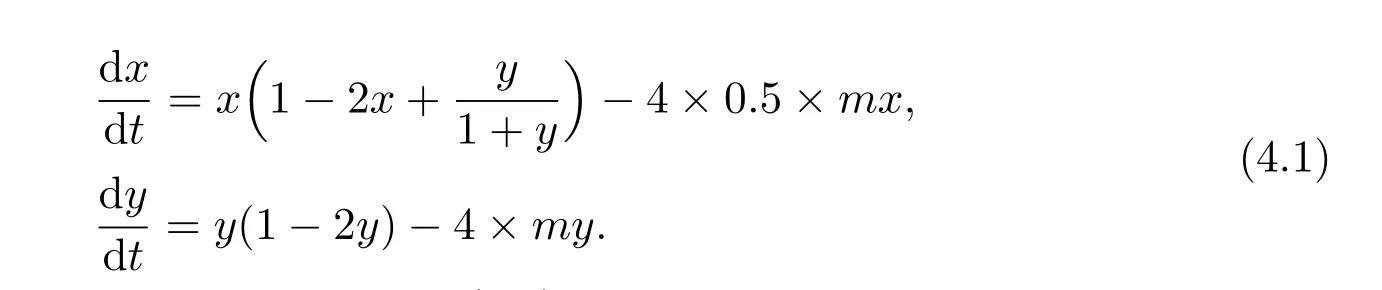


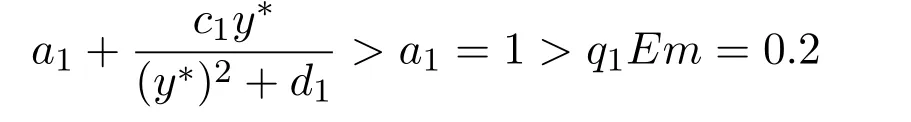
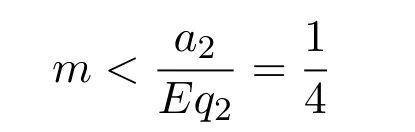

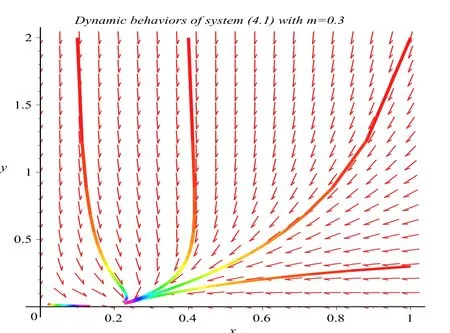
5 Conclusion
杂志排行
Annals of Applied Mathematics的其它文章
- DYNAMICS OF A PREDATOR-PREY REACTION-DIFFUSION SYSTEM WITH NON-MONOTONIC FUNCTIONAL RESPONSE FUNCTION∗†
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
- THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
- NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
- A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
