NEWDYNAMICINEQUALITIES FORDECREASING FUNCTIONS AND THEOREMS OF HIGHER INTEGRABILITY∗
2018-07-06SakerReganOsmanAgarwal
S.H.Saker,D.O’Regan,M.M.Osman,R.P.Agarwal
(1.Dept.of Math.,Faculty of Science,Mansoura University,Mansoura-Egypt;2.School of Math.,Statistics and Applied Math.,National University of Ireland,Galway,Ireland;3.Dept.of Math.,Texas A&M University-Kingsvilie,Texas,78363,USA)
1 Introduction
The classical integral Hölder inequality states that if f and g are positive measurable functions defined on

For generalizations and extensions in the literature we refer the reader to the papers[6–9,12–15].In this paper we establish some new dynamic inequalities on time scales.For related dynamic inequalities on time scales,we refer the reader to the books[1,2]and the papers[16,17].
The paper is organized as follows.In Section 2 we give a brief overview on time scales.In Section 3,we prove some new dynamic inequalities via convexity functions which contain inequalities given by Hardy,Littlewood and Pólya.We also establish some new dynamic inequalities on time scales for decreasing functions.These inequalities contain in particular generalizations of integral inequalities due to Hardy,D’Apuzzo and Sbordone and Popoli.We apply also these inequalities to prove a higher integrability theorem for monotone decreasing function on time scales.
2 Preliminaries on Time Scales
For a good introduction on time scales we refer the reader to the book[4].The forward jump operator and the backward jump operator are defined byσ(t):=inf{s∈T:s>t},andρ(t):=sup{s∈T:s

One chain rule is
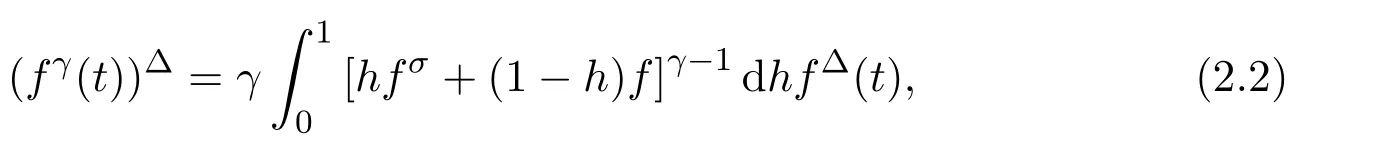
which is a simple consequence of Keller’s chain rule[4,Theorem 1.90].Another chain rule is as follows:Let f:R→R be continuously differentiable and suppose g:T→R is delta differentiable,then f◦g:T→R is delta differentiable and

In this paper we will consider the(delta)integral which we can be defined as follows.If F∆(t)=f(t),then the Cauchy(delta)integral of f is defined byf(s)∆s:=F(t)−F(t0).It can be shown(see[4])that if f∈Crd(T),then the Cauchy integralAn infinite integral is defined asIntegration on discrete time scales is defined by
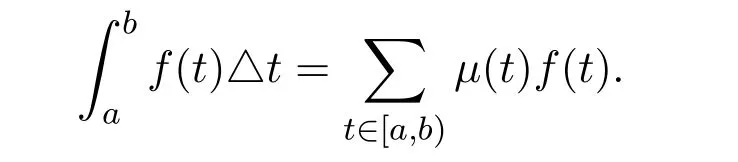
The integration by parts formula on time scales is given by
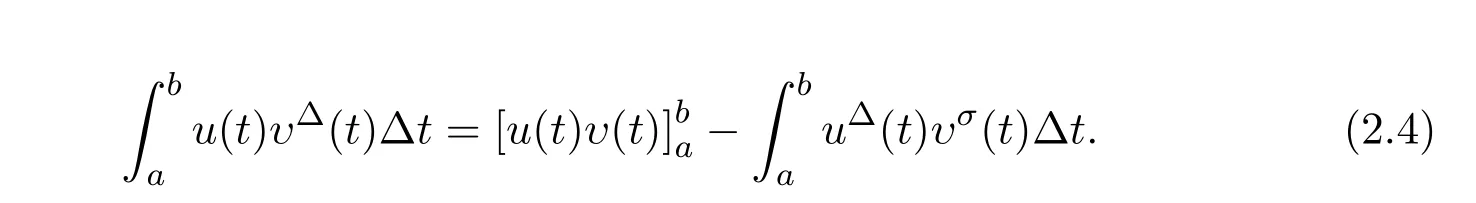
Hölder’s inequality[4,Theorem 6.13]states that two rd-continuous functions f,g:T→R satisfy
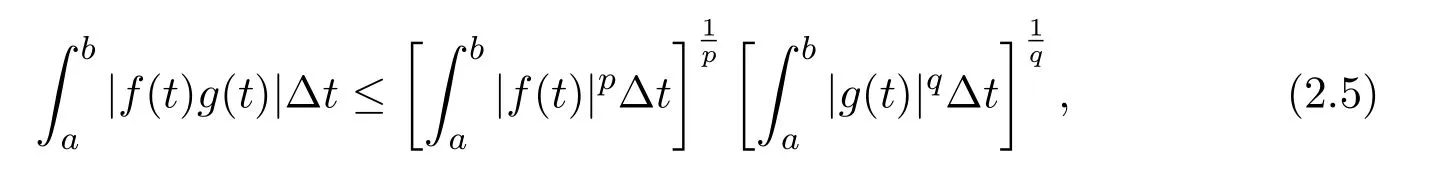
where p>1,1/p+1/q=1 and a,b∈T.
Throughout this paper,we will assume that the functions in the statements of the theorems are positive and the integrals considered are assumed to exist and are finite.
Next we present a weighted Hardy type inequality[16]on time scales which is useful in the proof of our main results.Without loss of generality,we assume that sup T=∞,and define the time scale interval[a,b]Tby[a,b]T:=[a,b]∩T.
Theorem 2.1LetTbe a time scale witha,b∈T(a In our next two results we will assume thatϕis a differentiable convex function. Theorem 3.1LetTbe a time scale with0,a∈T(a>0).Iffis decreasing then ProofLet x∈(0,a)T.Since f is a decreasing function, Let F(x)=so F is increasing.Note thatis a convex function,then From the chain rule(2.3)note Since F is increasing, Now from(3.2)and(3.3)we obtain so integration from 0 to a yields From this inequality we have(3.1).The proof is complete. A special case of Theorem 3.1 is given as follows whenϕ(u)=up,p>1. Corollary 3.1LetTbe a time scale with0,a∈T(a>0).Iffis decreasing then Remark 3.1Applying Hölder’s inequality on the right hand side of(3.6)we get the inequality Remark 3.2We consider the interval[a,b]Tand immediately we have Note if f is decreasing then xγ−1f(with γ ≤ 1)is decreasing.Use xγ−1f in(3.6)to obtain the following result. Corollary 3.2LetTbe a time scale with0,a∈T(a>0),p>1andγ≤1.Iffis decreasing then Remark 3.3Consider the interval[a,b]Tand assume that there exist positive numbers r and s with r In our next results we will assume that there exists an m>0 such that We apply now the weighted Hardy inequality(2.6)to prove a dynamic inequality. Theorem 3.2SupposeTis a time scale anda,b∈T(b>a),and assume(3.11)holds.Let Ifα≤1andβ>1,then where In particular ProofApplying inequality(2.6)with p=q= β,u(x)=(x − a)α−β−1and υ(x)=(x − a)α−1,we obtain here A=Cpand so Let t∈(a,σ(b))T.From the chain rule(2.2)we see that(noteα≤1 andβ>1) and as a result Let t∈(a,b)T.Apply the chain rule(2.2)and(3.11),then we have(noteα<β) and as a result From(3.15),(3.16)and(3.17)we have Putting(3.18)into(3.14),we obtain(3.13).The proof is complete. Letα=q/p andβ=q with p≥q>1 in(3.13)and we obtain the following Hardy-type inequality. Corollary 3.3SupposeTis a time scale anda,b∈T(b>a),p≥q>1,and assume(3.11)holds.Then wheremandGare defined in(3.11)and(3.12)respectively. Remark 3.4As a special case of Theorem 3.2 when T=R(note m=1),we have the inequality in[15,Theorem 2.1](note in our caseα≤1 andβ>1) where In particular when a=0 andα=1 we have Remark 3.5As a special case of Theorem 3.2 when T=N,a,b∈N,noting σ(x)=x+1 andwe have the discrete inequality Now we prove some lemmas that will be needed below. Lemma 3.1Suppose0<λ≤1and assume(3.11)holds.Let ProofFrom the definition of H and(3.11)we have Let u(x)=.Integrating the right hand side of(3.22),using formula(2.4)with u∆(x)=(x − a)λ−1and υσ(x)=h(t)∆t,we obtain(note Let t∈(a,b)T.Apply the chain rule(2.2)and we see that(note 0<λ≤1) and as a result The proof is complete. Lemma 3.2Letλ<0and suppose(3.11)holds.In addition assume Then whereHis defined in Lemma3.1. ProofProceed as in Lemma 3.1 and we obtain(note(3.23)) Let t∈(a,b)T.Apply the chain rule(2.2),and we see that(noteλ<0) and as a result The proof is complete. Lemma 3.3Letλ>1and assume(3.11)holds.Then whereHis defined in Lemma3.1. ProofFrom the definition of H(x)and(3.11)we have Let u(x)=Integrating the right hand side of(3.26),using formula(2.4)with u∆(x)=(σ(x)−a)λ−1and υσ(x)=∆t,we obtain(note Let t∈(a,b)T.Apply the chain rule(2.2),and we see that(noteλ>1) and as a result The proof is complete. In our next result we assume the nonnegative function f satisfies the reverse Hölder inequality,that is for x ∈ (a,b)Tthere exist some constants p,q with p Theorem 3.3LetTbe a time scale witha,b∈T(b>a),α<1and assume(3.11)holds.Suppose there exist constantsp,qwithp and hold.Then ProofLet where we let r=p and r=q.From(3.27)we have Apply Lemma 3.2 on the left-hand side of(3.29)withλ=α−1<0,h=fq(x),then we have Apply Theorem 3.2 on the right-hand side of(3.29)withβ=q/p(note p Substituting this into(3.29),we obtain Thus The proof is complete. Remark 3.6Consider the special case whenα=(and assume r>q)and p=1.Then we have see[7,Lemma 3.2]when T=R. Now we prove a higher integrability theorem for a monotone decreasing function on time scales. Theorem 3.4SupposeTis a time scale anda,b∈T(b>a),and assume(3.11)holds.Letfbe a decreasing function and suppose there exist constantsp,qwithp and holds.Then ProofFrom Theorem 3.3(withα=)we obtain Apply inequality(3.10)with r=q(note r=q Thus The proof is complete. Remark 3.7Since f is decreasing,we have f(σ(x))≤ f(x),so inequality(3.31)becomes [1]R.P.Agarwal,D.O’Regan and S.H.Saker,Dynamic Inequalities on Time Scales,Springer Cham Heidlelberg New York Drodrechet London,2014. [2]R.P.Agarwal,D.O’Regan and S.H.Saker,Hardy Type Inequalities on Time Scales,Springer International Publishing,Cham Heidlelberg New York Drodrechet London,2016. [3]R.Bibi,M.Bohner,J.Pecaric and S.Varošanec,Minkowski and Beckenbach-Dresher inequalities and functionals on time scales,Journal of Mathematical Inequalities,7:3(2013),299-312. [4]M.Bohner and A.Peterson,Dynamic Equations on Time Scales:An Introduction with Applications,Birkhäuser,Boston,2001. [5]M.Bohner and A.Peterson,Advances in Dynamic Equations on Time Scales,Birkhäuser,Boston,2003. [6]B.Bojarski,Remarks on the stability of reverse Hölder inequalities and quasi-conformal mappings,Ann.Acad.Sci.Fenn.Ser.A.I.Math.,10(1985),89-94. [7]L.D’Apuzzo and C.Sbordone,Reverse Hölder inequalities,A sharp result,Rend.di Mate.Ser.VII,10(1990),357-366. [8]F.W.Gehring,The Lp-integrability of the partial derivatives of a quasi-conformal mapping,Acta Math.,130(1973),265-277. [9]F.W.Gehring,The Lp-integrability of the partial derivatives of a quasi-conformal mapping,Bull.Amer.Math.Soc.,79(1973),465-466. [10]G.H.Hardy,J.E.Littlewood and G.Pólya,Some simple inequalities satisfied by convex functions,Messager of Math.,58(1929),145-152. [11]G.H.Hardy,J.E.Littlewood and G.Polya,Inequalities,second edition,Cambridge University Press,Cambridge,1952. [12]A.A.Korenovskii,The exact continuation of a reverse Hö lder inequality and Muckenhoupt’s conditions,Math.Notes,52(1992),1192-1201. [13]B.Muckenhoupt,Weighted norm inequalities for the Hardy maximal function,Trans.Amer.Math.Soc.,165(1972),207-226. [14]L.Nania,On some reverse integral in equalities,J.Austral.Math.Soc.,49A(1990),319-326. [15]A.Popoli,Optimal integrability inclasses,Le Matematiche,LII(1997),157-168. [16]S.H.Saker,R.R.Mahmoud and A.Peterson,Weighted Hardy-type inequalities on time scales with applications,Mediterranean Journal of Mathematics,13(2016),585-606. [17]S.H.Saker,R.R.Mahmoud,M.M.Osman and R.P.Agarwal,Some new generalized forms of Hardy’s type inequality on time scales,Mathematical Inequalities&Applications,20(2017),459-481.
3 Main Results


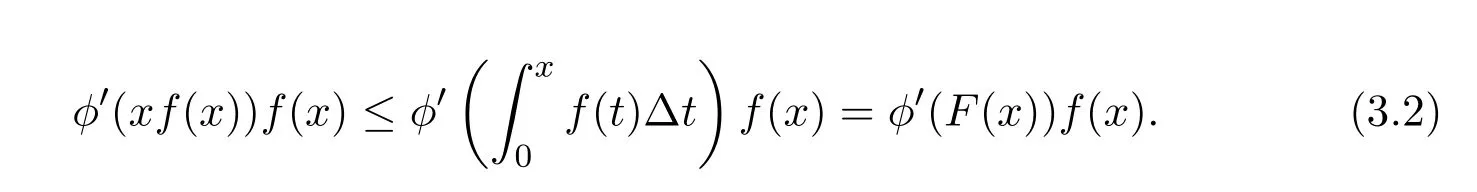






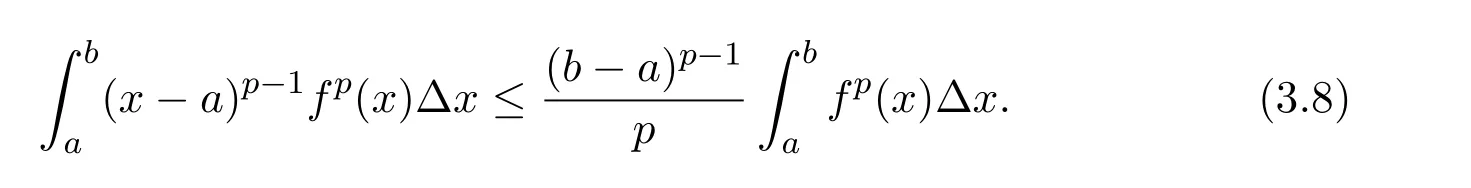

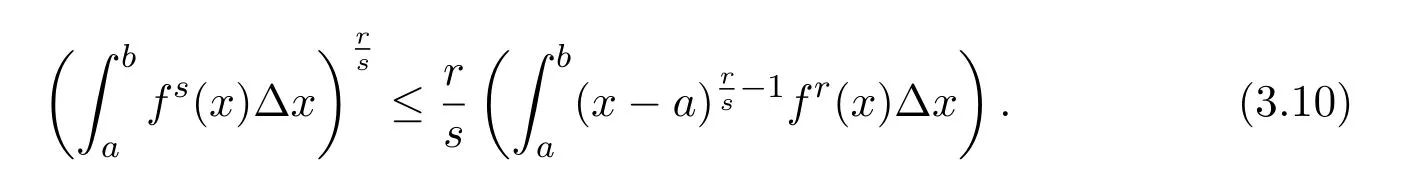
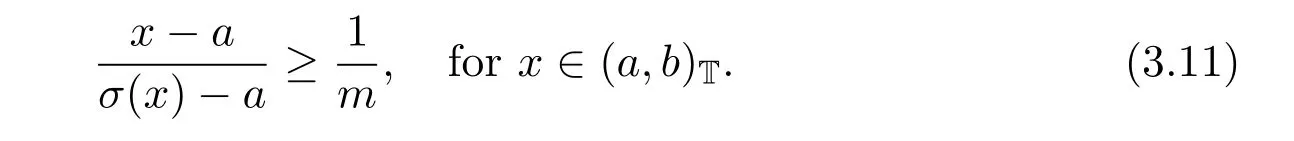
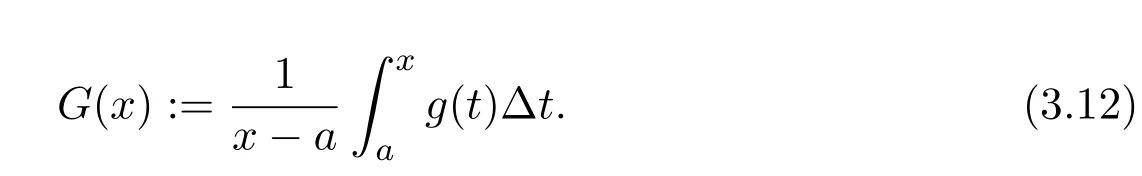

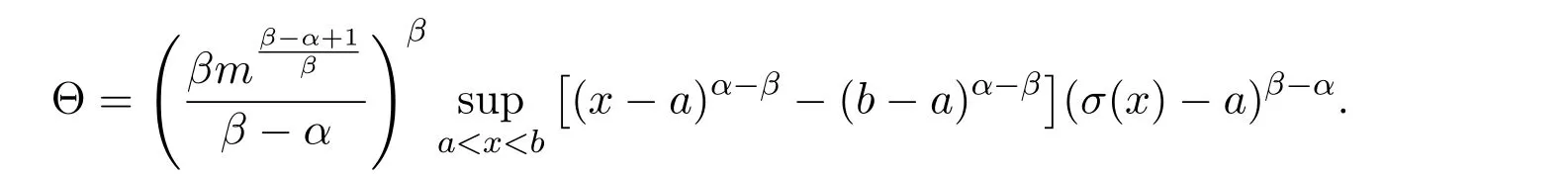


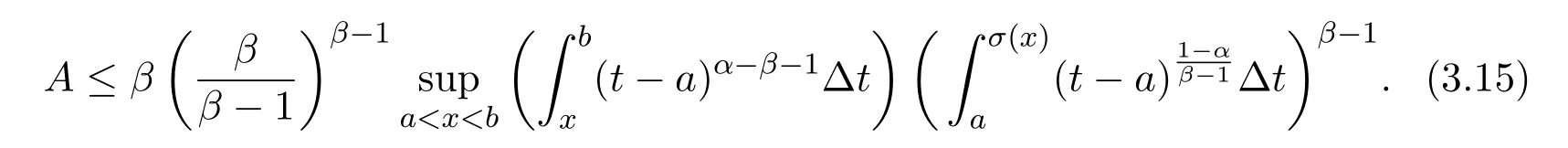
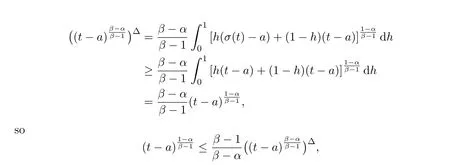

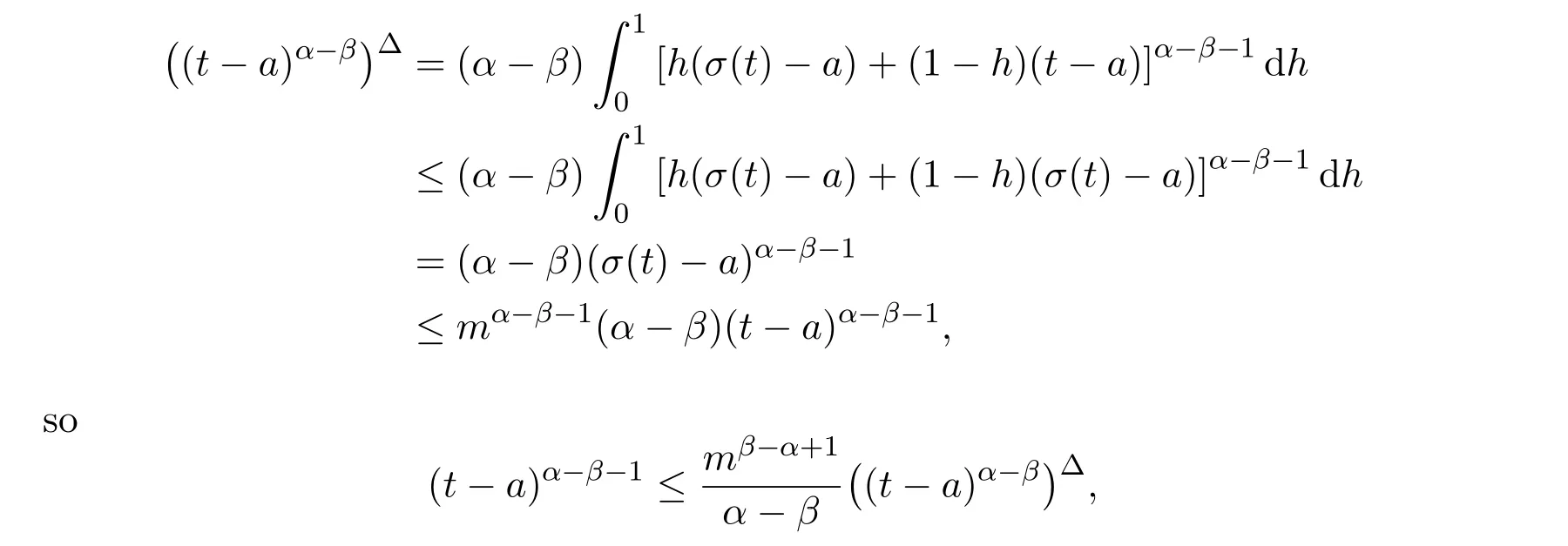





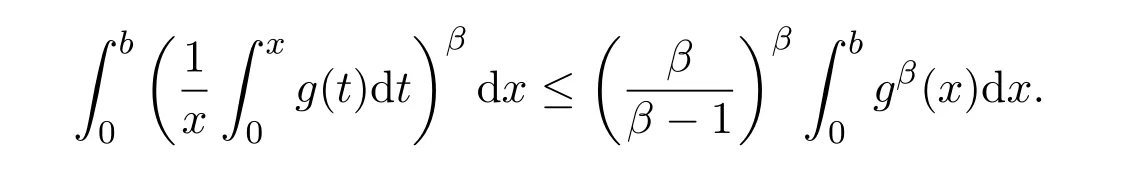



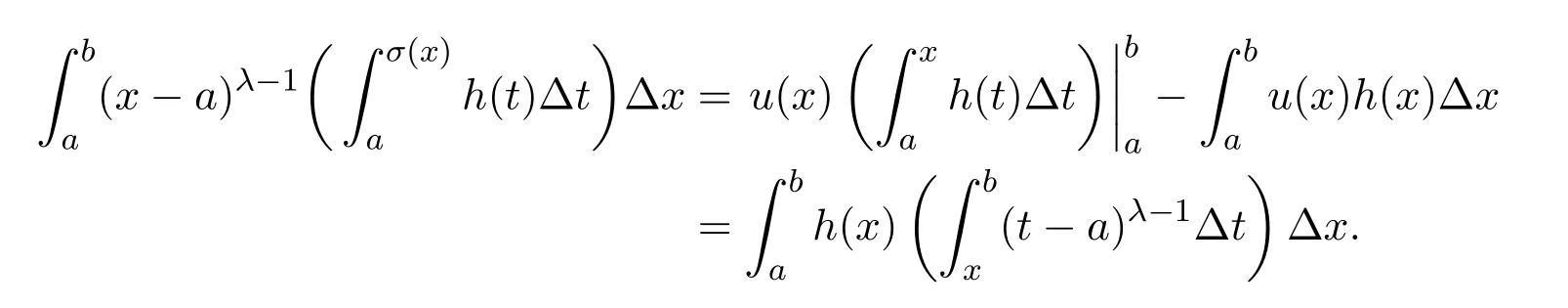

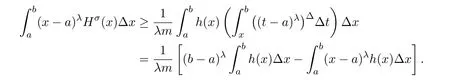





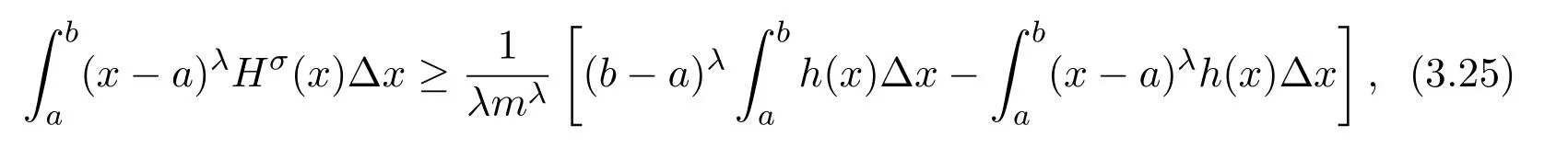
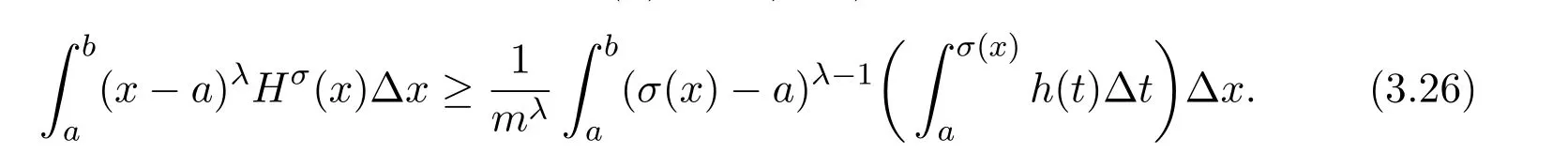


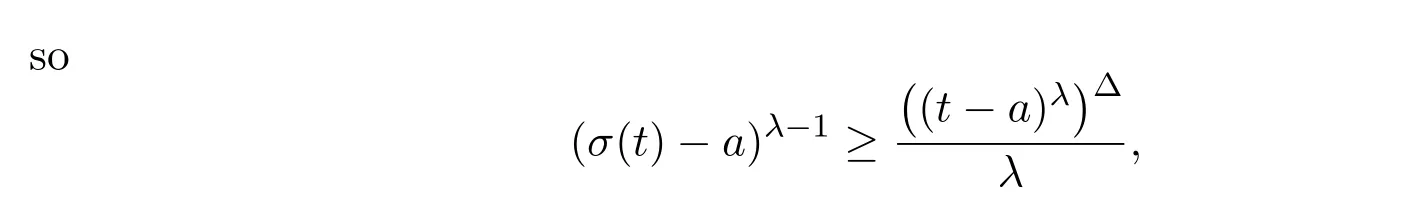

0 such that
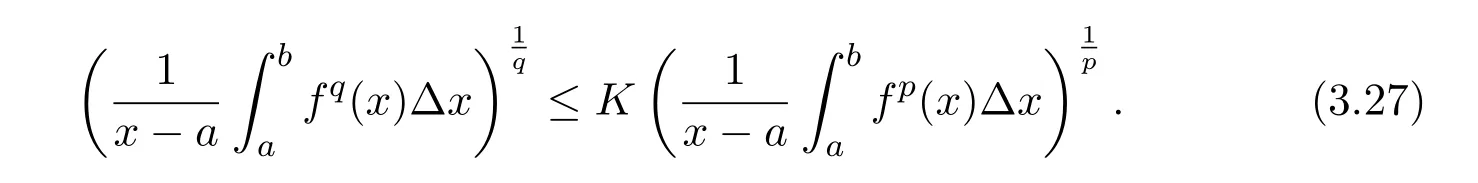

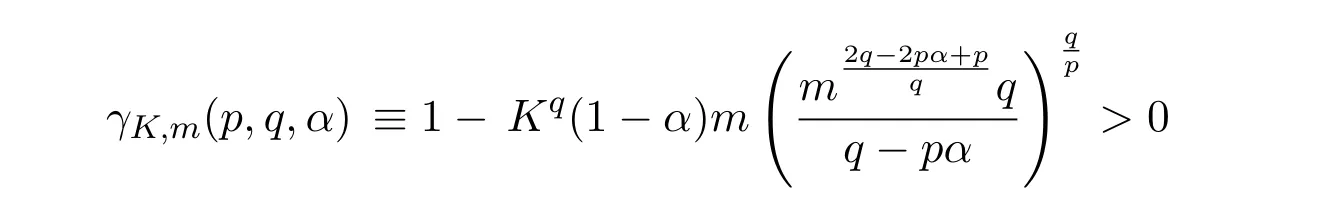
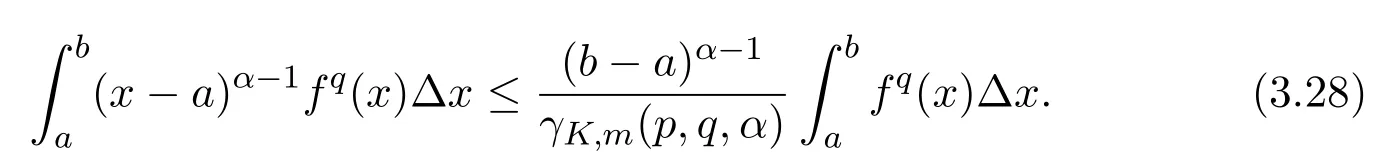
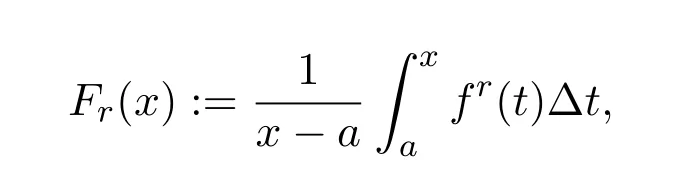
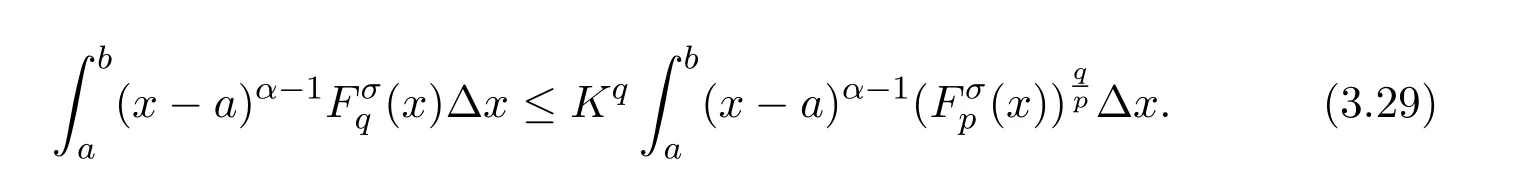
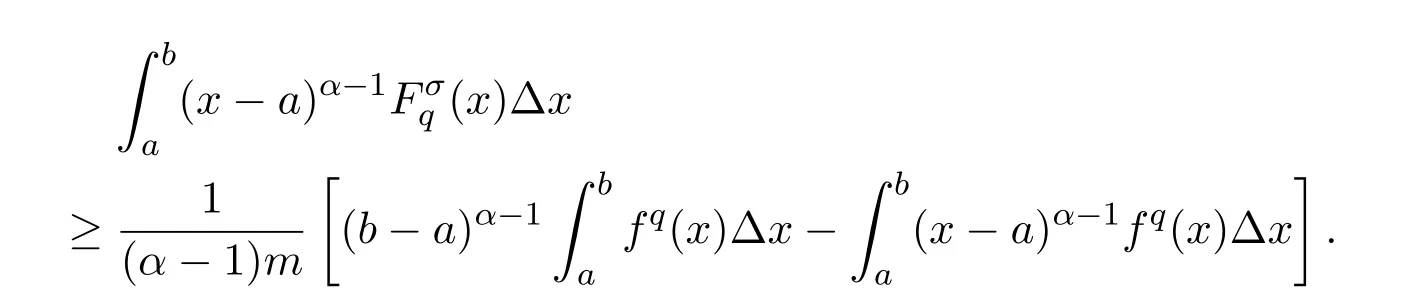



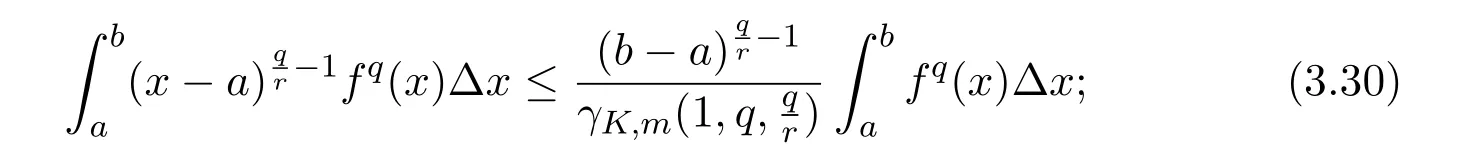
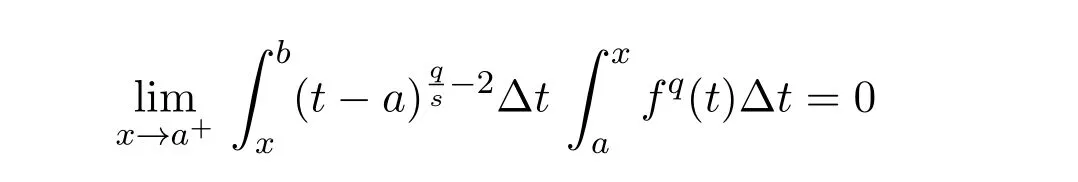
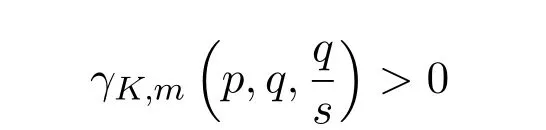


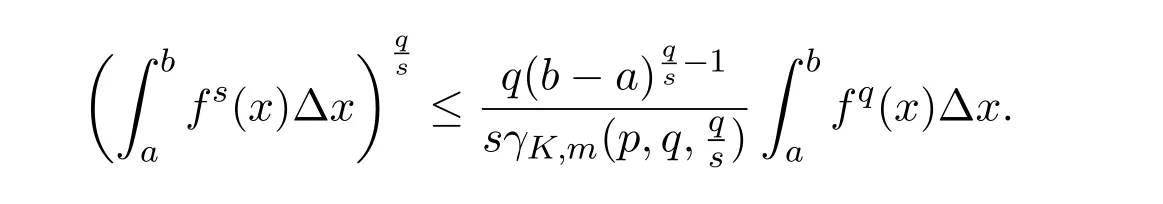


杂志排行
Annals of Applied Mathematics的其它文章
- DYNAMICS OF A PREDATOR-PREY REACTION-DIFFUSION SYSTEM WITH NON-MONOTONIC FUNCTIONAL RESPONSE FUNCTION∗†
- DYNAMICAL ANALYSIS OF A SINGLE-SPECIES POPULATION MODEL WITH MIGRATIONS AND HARVEST BETWEEN PATCHES∗†
- THE BOUNDS ABOUT THE WHEEL-WHEEL RAMSEY NUMBERS∗
- A COMMENSAL SYMBIOSIS MODEL WITH HOLLING TYPE FUNCTIONAL RESPONSE AND NON-SELECTIVE HARVESTING IN A PARTIAL CLOSURE∗†
- A BLOCK-COORDINATE DESCENT METHOD FOR LINEARLY CONSTRAINED MINIMIZATION PROBLEM∗†
- ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†
