ESTIMATION OF PARAMETERS IN A CLOSED PYGMY POPULATION IN CAMEROON∗†

Yannick Tchaptchie KouakepDavid Bekolle

(1.University of Ngaoundere,ERMIA,PO Box 454 Ndang,Ngaoundere,Cameroon;2.AIMS Cameroon,PO Box 608,Limbe,Cameroon;3.LYCLAMO/CES-HANGLOA,PO Box 46,Ngaoundere,Cameroon)

1 Introduction

Hepatitis B is endemic in Africa[23].There are few data updated on epidemiology of Hepatitis B in Africa,especially in Cameroon[17,21,25].But common measures and surveys on clinical cases show that average prevalence in Cameron is almost 10%and the average of prevalence for the three pygmy groups(the Baka,the Bakola and the Bedzan.)studied by Foupouapouognigni et al.[12]is around 11%.Since 20,000 years,the Pygmies have lived in a forest environment in Cameroon prominently as hunter-gatherers(Verdu et al.[20]).

HBV(Hepatitis B Virus)epidemiology in Cameroon social context briefly presented:

1)Professor Njoya Oudou,a specialist of Hepatitis diseases in[25]argues that 10 percent[3,17,25]of Cameroonians suffer from hepatitis B and need around USD 800 per month[5]for the treatment,even vaccination costs USD 50 per vaccinated individual[5].Total population of Cameroon is around 22 millions[21,24].

2)The relative importance of mother-child transmission of HBV(Hepatitis B virus)in Cameroon is not well known[17].

3)Treatments available for chronic hepatitis(not the acute one which is incurable)such as Interferon-alpha,Lamivudine,Adefovir or Entecavir[18]are expensive.Vaccine since 1981[3,18]GenHevac B protects 98%at least 10 years.

4)The rate of superinfection with other diseases such as hepatitis D is 25%[17,18].World Hepatitis day is held every year in July.

5)The maximal life span(years)is 51 years[21]and the birth rate is 32.49 per 1000[15]in Cameroon.

Our main result is to practically estimate HBV prevalences,the probabilityp(a)(to develop symptomatic Hepatitis B state at agea)and acute carriers’transmission rateβi.According to WHO[23]and Bonzi et al.[3],chronic carriers(most of time asymptomatic)have a low infectious rate.As a consequence in this work we assume thatβe≈0 compared withβi.The work is organized as follows.In Section 2,we present the model and estimate the parameters with least squares.Here we perform numerical simulations.Later in Section 3 we present results through evaluated prevalences and graphics.Finally we give a discussion in Section 4.

2 Model,Parameters Estimations and Numerical Simulations

2.1 Presentation of Cameroonian pygmy groups useful for our simulations

We now consider the tree pygmies seen as almost globally closed populations with 44700 to 56000 individuals studied in Foupouapouognigni Y.et al.[12],that is,the Baka group is the largest one(40,000 to 45,000 individuals),and its distribution overlaps the two administrative regions of the south and the east of Cameroon;the Bakola pygmies are the next most populous group(4,000 to 5,000 individuals),mostly located in the western part of the southern region in the Atlantic Ocean division;the Bedzan group is the smallest one(700 to 1,000 individuals)and is located in the northern part of the centralregion.According to Foupouapouognigni[12],HBV surface antigen(HBsAg)was screened by a third-generation EIA(Monolisa AgHBs Plus;Bio-Rad).Of the samples tested,there are 11.8%,95%CI,9.2 to 14.9%were positive for the three pygmy populations surveyed.

Pygmy populations(living in bush or mostly in forests)are relatively “closed”or isolated,and small,which can be a good example for our application[12].

2.2 Data and numerical simulations:Application to the largest pygmy group in Cameroon when R0>1

We recall again that simulating data coming from[12]is interesting because pygmy groups are almost small and closed populations living in deep forests with good properties for mass action law in respect of their way of life.

With these data of Foupouapouognigni Y.et al.[12]on the Baka pygmy population,we observe simulations on a maximum of timetmax=150 years with a maximal life spanA=60 years.We recall the assumption that Cameroon is in an endemic situation for HBV[12,17,23].

1a)We consider the following(chronological)age-structured and well posed model inspired by a manuscript of kouakep[16](through semigroup theory[2,11])with differential susceptibility and infectivity:

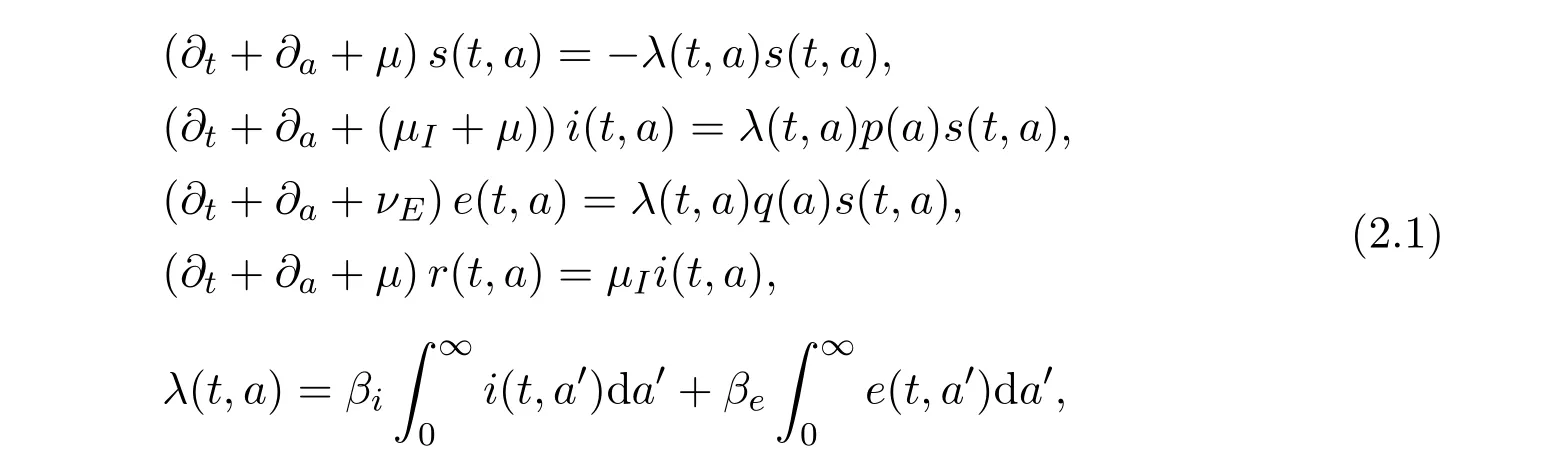
fort>0 anda>0.Heres(t,a)denotes the age-specific density of susceptible,e(t,a)andi(t,a)denote respectively the the age-specific density of chronic carriers and acute infected individuals(that can be symptomatic or asymptomatic)whiler(t,a)denotes the recovered individuals from acute infection.In additionp∈(0,∞)is a given function such that 0≤p(a)≤1a.e.whileq(a)≡1−p(a).Functionqrepresents the age-specific probability to become a(asymptomatic)chronic carrier when becoming infected at agea.Functionpdenotes the probability to develop an acute(symptomatic)infection when getting the infection at agea.We refer to Edmunds et al.[7]for more explanation on the age-dependence susceptibility to the infection.In order to take into account this age-specific susceptibility dependence we will use in this work a simplest prototypical shape curve of the form

for someκ∈[0,1]andr>0 estimated with least squares from data in[12].This differential susceptibility is a particularly important point for HBV infection.Recall that according to CDC1Centers for Disease Control and Prevention,USA:www.cdc.govabout 90%of children will remain chronically infected with HBV while 95%of adults will develop acute infection and will completely recover from HBV infection.

Parameterµ>0 denotes the natural death rate,νI:=(µI+µ)>0 andνEdenote the exit rates associated to each infected class.The termνIgathers recovery rateµIdue to acute infection and natural death rate whileνEcorresponds to the additional death rate due to chronic infection and its consequences.Here we neglect possible recovery from chronic disease.The termλ(t,a)corresponds to the agespecific force of infection and follows the usual bilinear law of mass-action,that is

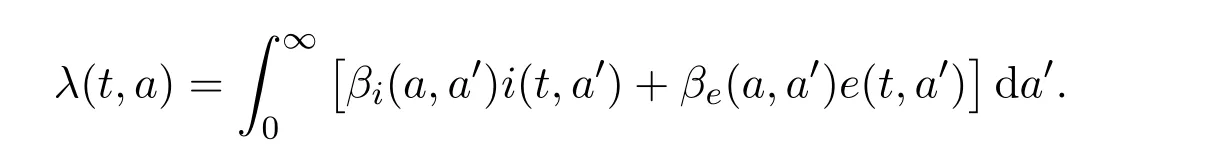
Hereβi(a,a0)andβe(a,a0)respectively denote the contact transmission rates of acute infected individual and asymptomatic carriers of agea0with susceptible of agea.We shall later assume that the contact between individuals is homogeneous so that

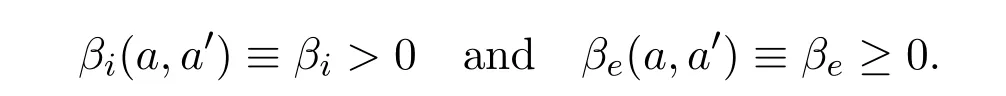
According to WHO[22,23],Edmunds et al[9]and Bonzi et al[3]chronic carriers(most of time asymptomatic)have a low infectious rate.As a consequence throughout of this work we assume that

This problem is supplemented together with the boundary conditions:

and initial data

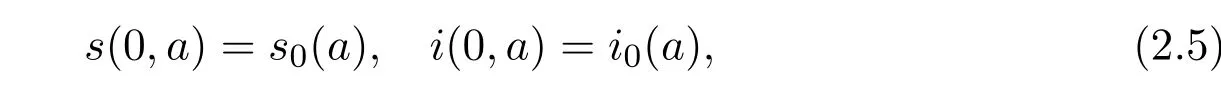
with

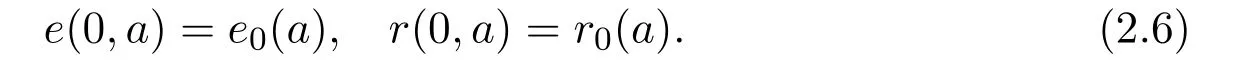
Note that ther-components of the system decouples from the other and have therefore no impact upon the long time behaviour of the system.It will be omitted in the sequel.Here we recall that the boundary conditionsi(t,0)=e(t,0)=0 correspond to no vertical transmission,that is also assumed in the sequel.Hence,as in the work of Edmunds et al.[7,8],we shall focus,in this work,on horizontal transmission taking into account age-specific susceptibility.This age-structured model(2.1)-(2.6)generalizes a discrete age one presented by Bonzy et al.[3,Fig.3,page 62].We introduce the threshold parameterR0known as basic reproduction number(Dietz[4]1975)defined by[16]as

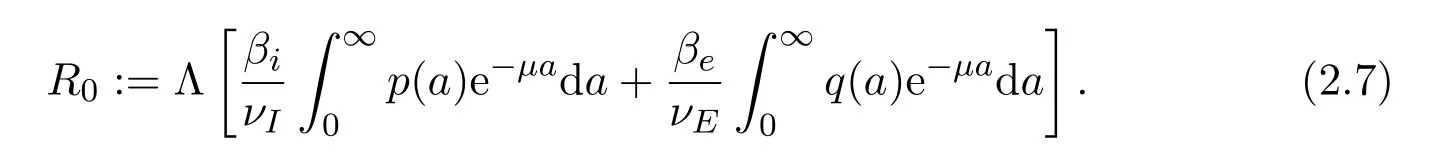
We set

and

1b)It is easy to see that at endemic steady state(se,ie,ee,re)we get

which is obviously positive and unique as solution of a decreasing function goes to 0 sinceR0>1.And we obtain the following system of ordinary differential equations satisfied by the unique endemic equilibrium(se,ie,ee,re):

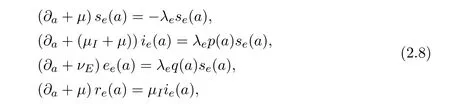
This problem is supplemented together with the boundary conditions:

The model(2.1)-(2.6)could be rewritten as an abstract Cauchy problem

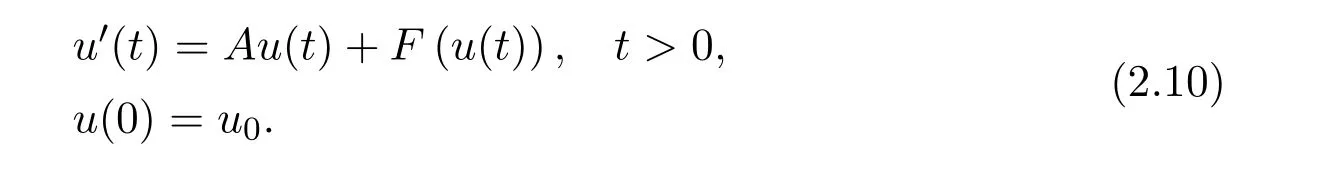
This can be seen as a Lipschitz perturbationFof a nondensely defined Hille-Yosida operatorAand then prove its well posedness on suitableL1-like positive cones with the integrated semigroup approach(see explanations in Kouakep[16]or Djidjou et al.[5,6]).Then standard methodologies[5]apply to provide the existence and uniqueness of mild solution for system(2.1)-(2.6).

2.3 Method of least squares for parameters’evaluation

1)Our aim is to compare the specific class prevalencestatistically adjusted from data[12]and estimated prevalence(pi)from model(2.1)-(2.6)for the seven classes in the Table 1.

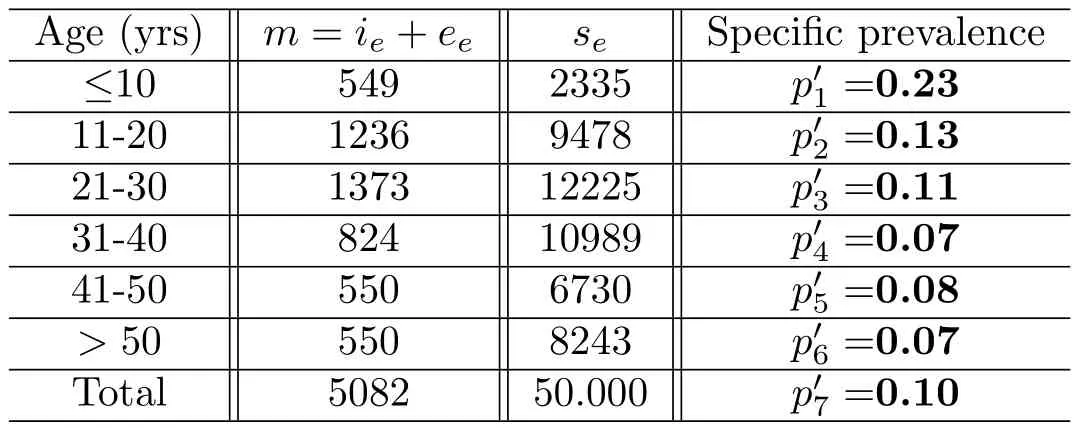
Table 1:HBV data for Baka pygmy group[12]adjusted for 50000 individuals

2)Knowing thatq(a)=ue−v a≡0.643e−0.156aandp(a)=1−q(a),we get:

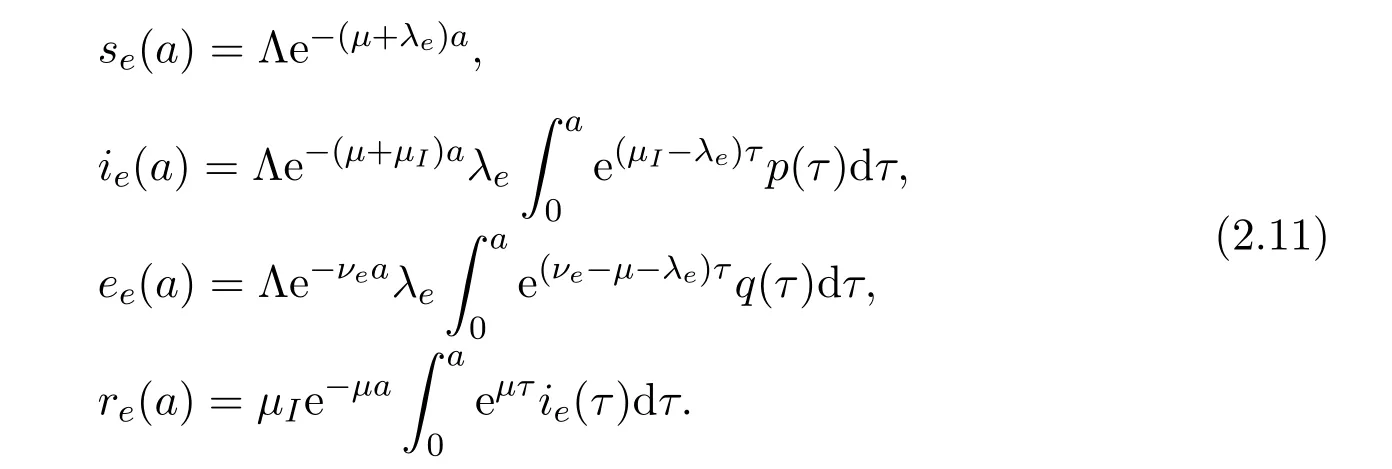
3)We obtain for thei-th age class[a1(i);a2(i)]in Table 1,the evaluation of the estimated prevalence as

4)We set

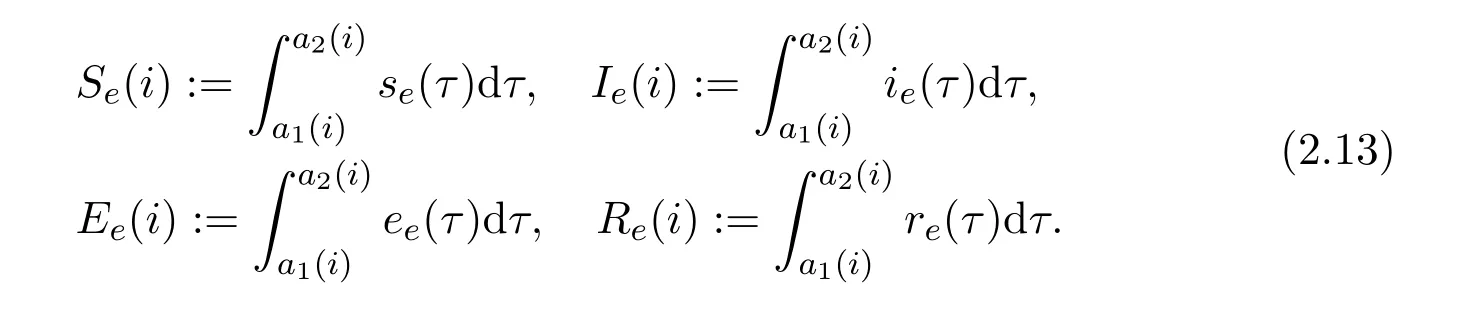
5)We present then the Baka HBV acute prevalences in Table 1.But it is difficult to obtain with formula of the endemic equilibrium,for∆ie,ee=(ie(a1)−ie(a2))+(ee(a1)−ee(a2))the form

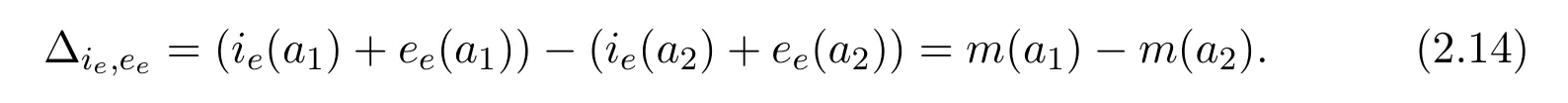
According to[14],it is possible to defineeein respect toie(withm(a):=(ie(a)+ee(a))):

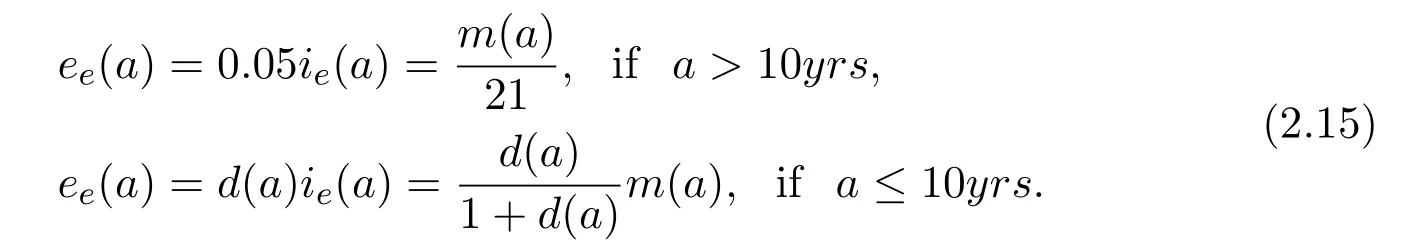
withd(a)∈[0.3;0.9]or simplyd(a)=d∗=0.6(see also Goyal et al.[13]).

6)One can theoretically solve the six(resp.seven)nonlinear equations

in order to findβi,βe,Λ,λe,µI,νe(resp.withµfori=7).

7)But practically,we can approximatewith Table 1 provided by[12]and these coefficients numerically with the likelihood maxima or(as in this work)the least squares methods.

2.4 Simulations and evaluation of some coefficients in the case R0>1

Practically,while estimatingβi,βe,Λ,λe,µIandνe:

1)We use the least squares method with≤µI≤26,since the average timespending in the acute class/compartment belongs to[2,6](in weeks).

2)The maximal life spanAplays a great role on prevalence estimations.One can modify also the numerical codes to estimated(a)=d∗.In fact,by varying the value ofd∗between 0.3 and 0.9,we obtain similar observations as above.

3)Then with numerical constraint onµI,we can estimate the transmission coefficient of acute infectiousβiby assuming thatβe≈0[3,22]and

3.a)theoretically:

3.b)practically:by considering maximum age at 60 years that is just beyond the maximal life span in Cameroon.

We made simulations with the values in Table 2(by using the software(c)Scilab).We denote in Table 2: “p” for people,“yr” for year and “ofs” for off spring or births.

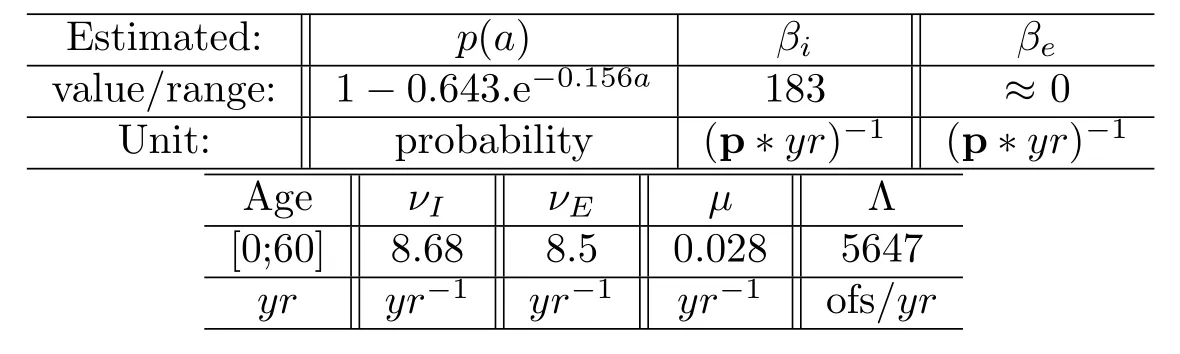
Table 2:Values for R0=2.67>1 estimated with(2.7)

3 Results

A)Using Table 1,the least squares approximations provide the curve 1 of the functionq:a→q(a)=1−p(a).

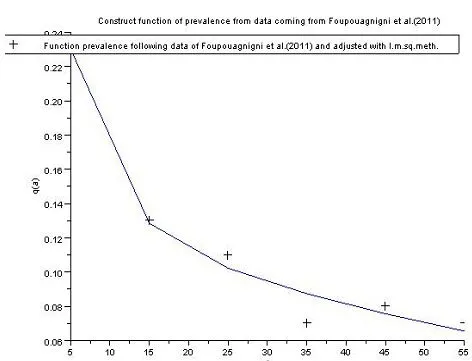
Figure 1:Function q:a→q(a)=1−p(a)adjusted from data of Foupouapouognigniet al.[12]

B)The estimated prevalences are provided in Table 3.We obtain then Figures 2 to 4 presented therein,which show the numerical stability of the endemic equilibrium for long time dynamics of the model.

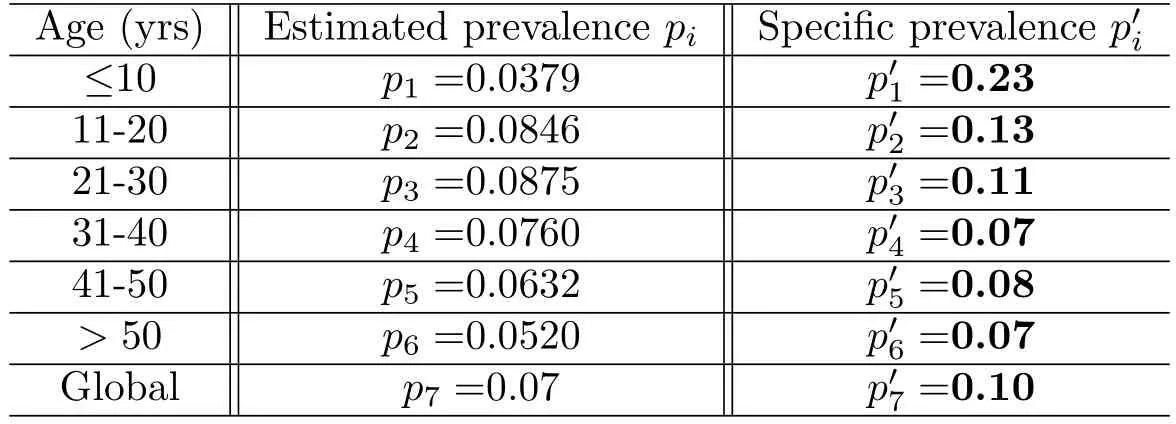
Table 3:Baka data,estimated prevalence VS real specific prevalences for the Baka pygmy group following[12]adjusted to 50000 individuals R0=2.67>1

Figure 2:Prevalence estimated per time

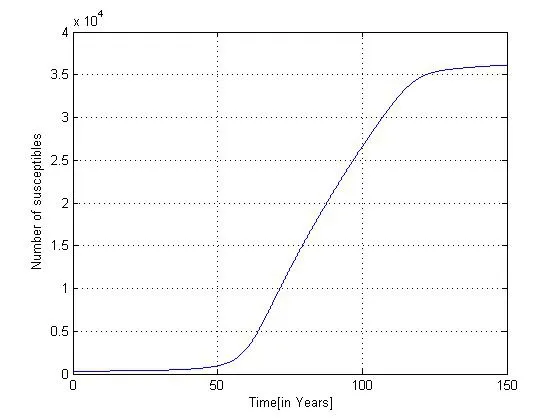
Figure 3:Function of susceptible’density per time

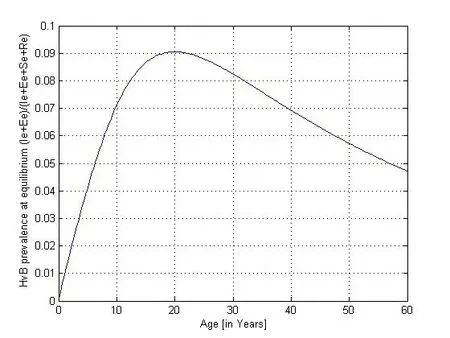
Figure 4:Estimated prevalence at equilibrium

4 Discussion

The above example with differential susceptibility and age structure shows that it is possible to estimate interesting parameters from biological data.

We estimate parameters in Table 2 from(Foupouapouognigni et al.[12],2011)on Baka pygmy group in the East Cameroon region.The gap on Figure 4 for small ages is probably due to the fact that vertical transmission is neglected[5,6,19]in Cameroon[1](See the first three lines of Table 3).Moreover the last line indicates a gap at age less than 10 years.We obtain similar results with the general functionq(a)=exp(−0.645a0.455)stated in(Edmunds et al.[7]1993).The valueR0=2.67>1 of the basic reproduction number estimated from data in[12]confirms that HBV is endemic in the Baka pygmy group.

We need to point out the fact that this modelleft out the vaccination since it is very expensive in Africa,especially in the population studied in Cameroon.Further investigations will be done to include a prospective campaign of mass vaccination for children and young adults in an extended version of(2.1)-(2.6)and estimate parameters.Studies including verticaltransmission like those of(El-Doma[10]2006)could be used in Chinese case as[5]ifwe modify them in order to add the hypothesis of differentialmortality according to susceptible,acute or carrier classes as in model(2.1)-(2.6).

5 Acknowledgment

The author would like to thank Dr A.Ducrot,Prof.Houpa D.D.E.,Prof.Ntyam Achille and GDM-MIAP student group for their helpful suggestions.The author is solely responsible for the views and opinions expressed in this research(part of YTK’s PhD);it does not necessarily reflect the ideas and/or opinions of the funding agencies(AIMS-NEI or IDRC),LYCLAMO and University of Ngaoundere.

[1]Anfumbom K.W.Kfutwah,M.C.Tejiokem and R.Njouom,A low proportion ofHBeAg among HBsAg-positive pregnant women with known HIV status could suggest low perinatal transmission of HBV in Cameroon,Virology Journal,9(2012),1-4.

[2]W.Arendt,C.J.K.Batty,M.Hieber,and F.Neubrander,Vector-valued Laplace Transforms and Cauchy Problems,(2nd edition),Birkhauser Verlag,2011.

[3]B.Bonzi,A.A.Fall,A.Iggidr,and G.Sallet,Stability of differential susceptibility and infectivity epidemic models,J.Math.Biol.,62:1(2011),39-64.

[4]K.Dietz,Transmission and control of arbovirus diseases.In:Epidemiology,D.Ludwig,K.L.Cooke,(eds.),Philadelphia:Society for Industrial and Applied Mathematics,pp.104-121,1975.

[5]R.Djidjou,J.Tewa,S.Bowong and Y.Emvudu,Optimal control for an age-structured modelfor the transmission of hepatitis B,J.Math.Biol.,73:2(2016),305-333.

[6]R.D.Demasse,J.J.Tewa and S.Bowong,Analysis of an Age-structured SIL model with demographics process and vertical transmission,Special issue CARI’12 in ARIMA Journal,17(2014),23-52.

[7]W.J.Edmunds,G.F.Medley,D.J.Nokes,A.J.Hall and H.C.Whittle,The influence of age on the development of the hepatitis B virus(HBV)carrier state,Proc.Roy.Soc.London,253B(1993),197-201.

[8]W.J.Edmunds,G.F.Medley and D.J.Nokes,The design of immunization programmes against Hepatitis B virus in developing countrie,in Models for Infectious Human Diseases:Their Structure and Relation to Data,V.Isham and G.Medley,eds.,Cambridge University,Cambridge,1996,pp.83.

[9]W.J.Edmunds,G.F.Medley and D.J.Nokes,The transmission dynamics and control of hepatitis B virus in the Gambia,Stat.Med.,15(1996),2215-2233.

[10]M.El-Doma,Analysis of an SIRS age-structured epidemic model with vaccination and vertical transmission of disease,Applications and Applied Mathematics,1:1(2006),36-61.

[11]K.J.Engel and R.Nagel,One Parameter Semigroups for Linear Evolution Equations,Springer-Verlag,New York,2000.

[12]Y.Foupouapouognigni,S.A.Sadeuh Mba,A.E.B.Betsem,D.Rousset,A.Froment,A.Gessain,R.Njouom,Hepatitis B and C virus infections in the three pygmy groups in Cameroon,J.Clin.Microbiol.,49:2(2011),737-40.Epub 2010.Epub 2010 Nov 24.PubMed PMID:http://www.ncbi.nlm.nih.gov/pubmed/21106785 or www.ncbi.nlm.nih.gov/pmc/articles/PMC3043525/pdf/zjm737.pdf

[13]A.Goyal,J.M.Murray,The Impact of vaccination and antiviral therapy on hepatitis B and hepatitis D epidemiology,PLoS One,9:10(2014),e110143.

[14]Hépatoweb,http://www.hepatoweb.com/hepatite-B-infection.php,accessed on January 31,2013.

[15]Index Omundi,Source: CIA World Factbook,January 1,2012 Version,http://www.indexmundi.com/g/r.aspx?c=cm&v=25&l=fr,accessed on January 31,2013.

[16]Y.T.Kouakep,Perturbation of a globally stable equilibrium:application on an agestructured model,Sao Paulo Journal of Mathematics Sciences,2016:1(2016),1-26.

[17]Ministry of Public Health of Cameroon, Plan D’introduction du vaccin contre l’Hépatite virale B dans le PEV de routine 2005-2009, pp.9.http://www.gavialliance.org/country/cameroon/documents/proposals/vaccine-introduction-plan-for-nvs|hep-b-support-cameroon-fran%C3%A7ais-/,accessed on January 31,2013.

[18]Pasteur Institute,Infectious diseases:hepatitis B and C,http://www.pasteur.fr/ip/easysite/pasteur/fr/presse/fiches-sur-les-maladies-infectieuses/hepatites-b-et-c,accessed on January 31,2013.

[19]A.Sall Diallo,M.Sarr,Y.Fall,C.Diagne,M.O.Kane,Hepatitis B infection in infantile population of Senegal,Dakar Med.,49:2(2004),136-142.

[20]P.Verdu,et al.,Origins and genetic diversity of pygmy hunter-gatherers from Western Central Africa,Curr.Biol.,19(2009),312-318.

[21]WHO,Cameroon,http://www.who.int/countries/cmr/en/index.html,accessed on January 31,2013.

[22]WHO,Hepatitis B and breastfeeding,No.22,November 1996.

[23]WHO,Media centre:Hepatitis B,http://www.who.int/mediacentre/factsheets/fs204/en/index.html,accessed on January 31,2013.

[24]World Bank,indicator of total population,http://data.worldbank.org/indicator/SP.POP.TOTL,accessed on June 30,2015.

[25]10 per cent of Cameroonians suffer from hepatitis,http://www.seronet.info/breve/10-camerounais-sur-100-souffrent-dhepatites-28377,accessed on January 31,2013.