四元数互补滤波的机械手手势姿态解算

吴 聪, 刘 俊

(上海电机学院 a. 电气学院；b. 机械学院，上海 201306)

在现代工业领域，远程控制的机械手得到了广泛应用。基于多传感器融合的远程控制机械手已成为研究热点，在危险应急的场合有不可替代的作用。基于多传感器融合控制机械手是利用传感器传输手部的参数信息，进而获取运动信息。要完成对机械手的控制首先要获取传感器传输的控制信息,通过构建手势姿态运动系统来得到这一信息。惯性导航系统是将惯性传感器直接固连在载体上[1]，手势姿态运动系统则是将传感器固定在手部的相应位置，利用计算机中的导航程序建立起姿态，通过惯性传感器得到载体信息的同时更新姿态矩阵和解算航姿参数，通过在机械手上的惯性器件(如加速度计,陀螺仪等)定时测定得到机械手的即时运动参数，通过姿态解算算法，解算出机械手的运动姿态。被应用在控制器姿态角上的数据融合算法有互补滤波[2]、共轭梯度法滤波[3]、扩展卡尔曼滤波( EKF)[4]和无迹卡尔曼滤波(UKF)[5]。互补滤波原理简单，能够滤去噪声和抑制漂移，确定合适的低通截止频率对加速度计采集到的数据进行预处理，操作简便，处理后的数据也能有效地完成四元数算法。首先利用加速度计测得重力向量与估计姿态得到的重力向量的误差来矫正积分误差，然后利用矫正后的积分得到所需要的姿态角。在姿态角的解算中，常用的有欧拉角法、方向余弦法和四元数法。文献[6]中在欧拉角描述体系下，采用迭代的EFK组合多传感器测量信息的方法对无人机的姿态进行测量。该方法与常规的方法相比能够较准确的测量姿态角的信息，但是当俯仰角接近90°时方程会出现奇点，故该方法只适合于姿态角变换不大的范围，不能进行全姿态解算；文献[7-8]中提到的方向余弦法虽然解决了欧拉角法不能进行全姿态的解算，但是解9个未知量的方程计算量过大，实时计算困难，工程中很少使用。

本文提出采用四元数互补滤波的方法解算姿态角[9-12]。获取的姿态角是载体相对于初始坐标系的量，为了求解姿态角，要弄清楚载体运动坐标系与初始坐标系，初始坐标系与地球坐标系的坐标变换关系。所以求解姿态角的过程就是获取两个坐标系之间变化关系的过程。

1 手势运动系统姿态测量

传感器不能直接测量控制器的姿态角，因此，需要利用惯性传感器测量的数据信息进行姿态解算，进而控制机械手的运动信息。

1.1 手势运动系统参考坐标系

对任何系统的运动研究都是在特定的参考坐标系内完成的，对手势运动系统的坐标系设计如下：

(1) 机械手初始坐标系，简称G系，坐标三轴用XgYgZg表示。该坐标系原点的位置时刻代表着载体的位置，它不参与载体自身的转动[13]。即机械手的曲腕部分，曲腕部分不参与转动，表示机械手在运动过程中的实际地理位置。

(2) 机械手运动坐标系，简称B系，坐标三轴用XbYbZb表示。机械手运动坐标系是与载体固联参与载体运动的坐标系，代表载体的姿态[13]。这部分坐标系代表机械手五指控制的运动姿态。

1.2 载体手势姿态角的定义

在手势运动系统中，将惯性传感器直接固联在机械手上，运动学中常用偏转角ψ、俯仰角θ和横滚角γ[13]描述载体相对于运动坐标系中的姿态角，定义机械手右、前、上3个方向构成右手系：

偏转角ψ(yaw)：机械手绕定义向上的Z轴旋转与地理北极之间的夹角，顺时针旋转为正，定义域为0～360°。

俯仰角θ(Pitch)：机械手绕定义向右的Y轴旋转与水平面之间的夹角，向上为正，向下为负，定义域为-90°～+90°。

横滚角γ(rool)：机械手绕定义向前的X轴旋转与水平面垂直平面之间的夹角，右倾为正，左倾为负，定义域为-180°～+180°。

机械手的运动姿态由偏转角、俯仰角、横滚角来描述，三维空间机械手运动系统坐标系如图1所示。根据初始坐标系与运动坐标系之间位置变换来解算姿态角[10]。初始坐标系与运动坐标系之间的角度转换如图2所示。

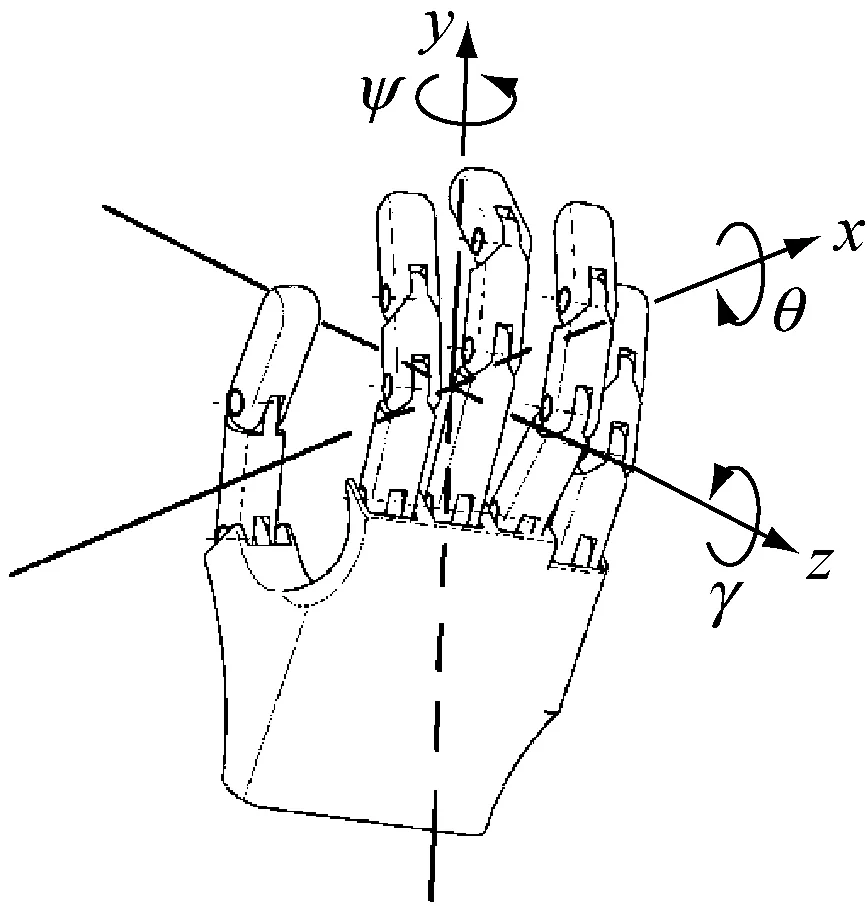
图1 三维空间机械手运动系统坐标系

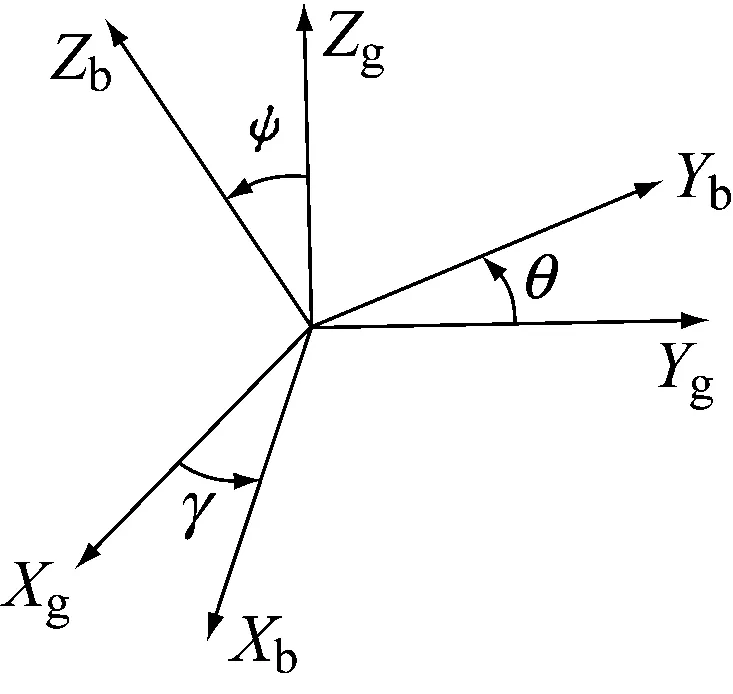
图2 初始坐标系与运动坐标系角度变换

1.3 坐标变换连接矩阵

上文提到求解姿态角的过程就是获取两个坐标系之间变化关系的过程。两坐标系之间角位置关系可以分解为有限次的基本旋转，经过旋转可得两坐标系之间的变化为

(1)

(2)

此时，T矩阵被称为姿态矩阵。

固定在载体上的传感器测得姿态参考向量在运动坐标系各轴的投影，而姿态信息的解算在初始坐标系进行。因此，首先要将姿态参考向量投影到初始坐标系，这个转换是由运动坐标系到初始坐标系变换矩阵完成，根据矩阵中的元素可以求取载体的姿态角。

2 四元数法解算姿态

四元数(Quaternions)是由威廉·卢云·罕密尔顿[14-15]在1843年爱尔兰发现的数学概念。简单地说四元数是由1个实数单位1和3个虚数单位i，j，k组成的含有4个元的数，其表达式为

(3)

由刚体定点转动理论中的欧拉定理可以得到结论：动坐标系相对于参考坐标系的方位可以由动坐标系绕某一转轴μ转动一个角度θ，所以动坐标系的方位可有参数μ和θ来确定。构造一个四元数

Q=cos(θ/2)+μsin (θ/2)

(4)

得载体坐标系到导航坐标系变换的四元数形式为

(5)

对式(4)求导，可得四元数微分方程式为

(6)

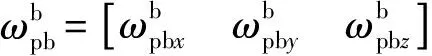
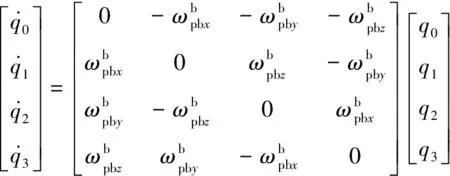
(7)

可用毕卡法解此方程。

3 四元数计算姿态角的实现

根据前面给出的姿态解算方程与四元数，即可得到姿态计算系统的计算原理如图3所示。

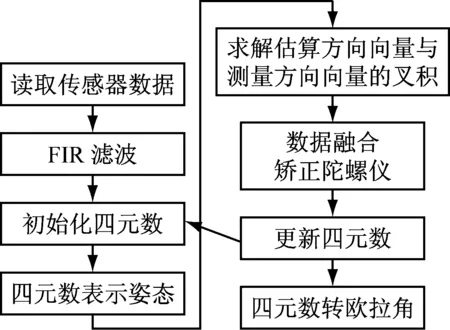
图3 姿态算法流程图

3.1 低通滤波器的实现

实际算法实现中，由于加速度计对外界力敏感， 特别是操控的机械手在启动时的抖动会对加速度计的数据有很大干扰，如图4所示，而加速度计不自带低通滤波，所以，为加速计的数据设计了低通滤波器来对数据进行预处理。

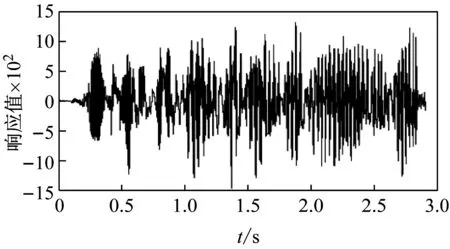
图4 Matlab加速度计未滤波时域

首先通过串口采集到了加速度计的原始数据，加速度计数据输出速率初始化为800 Hz，将数据导入Matlab,做FFT变换得到频谱如图5所示。

由图5可知噪声分布主要在400 Hz左右。结合实际情况，选择基于凯赛窗的低通滤波器，带通频率100 Hz,带阻频率200 Hz，利用Matlab计算出滤波器参数，滤波后效果如图6所示。经过滤波器后加速度数据可用。

3.2 四元数算法的实现

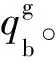
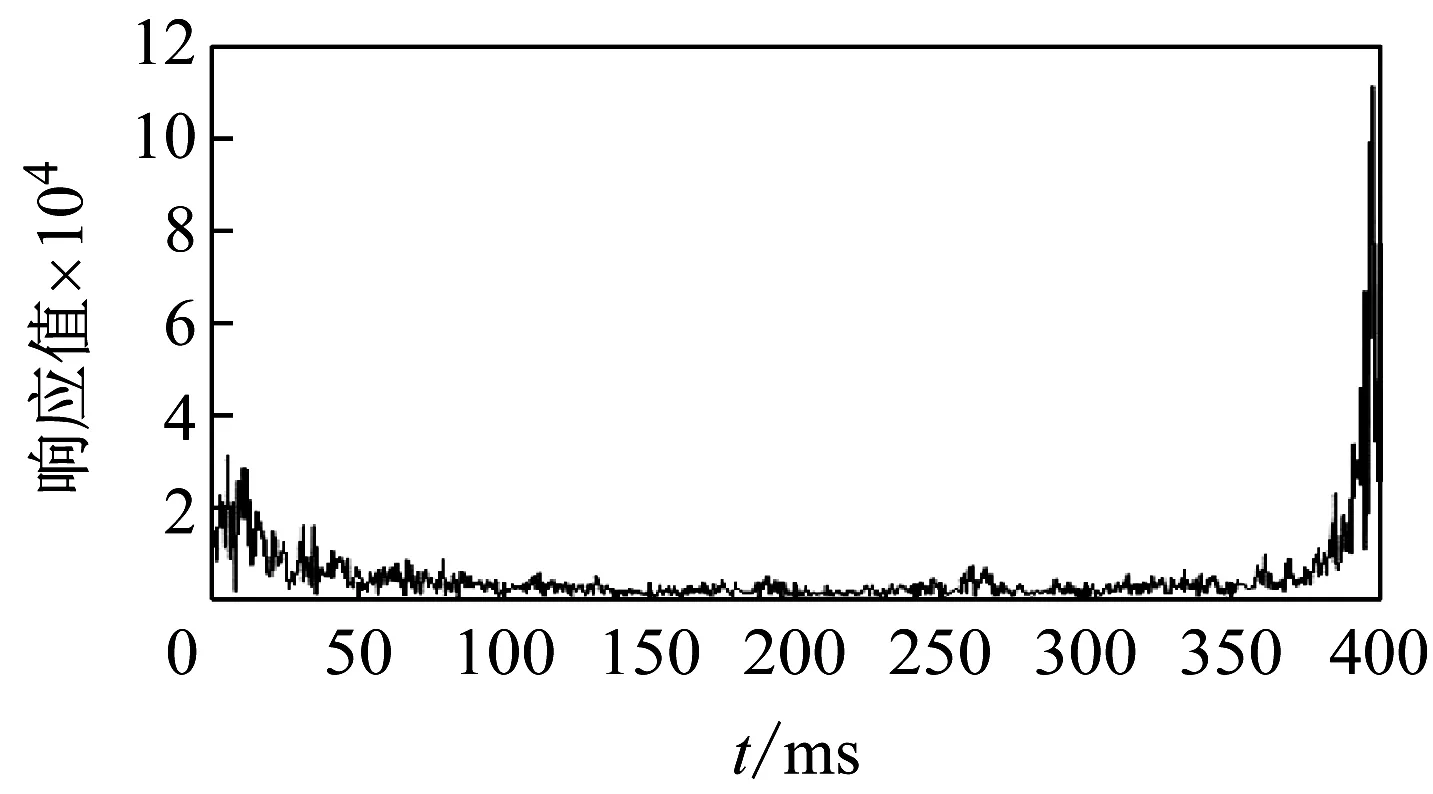
图5 Matlab加速度计未滤波频域

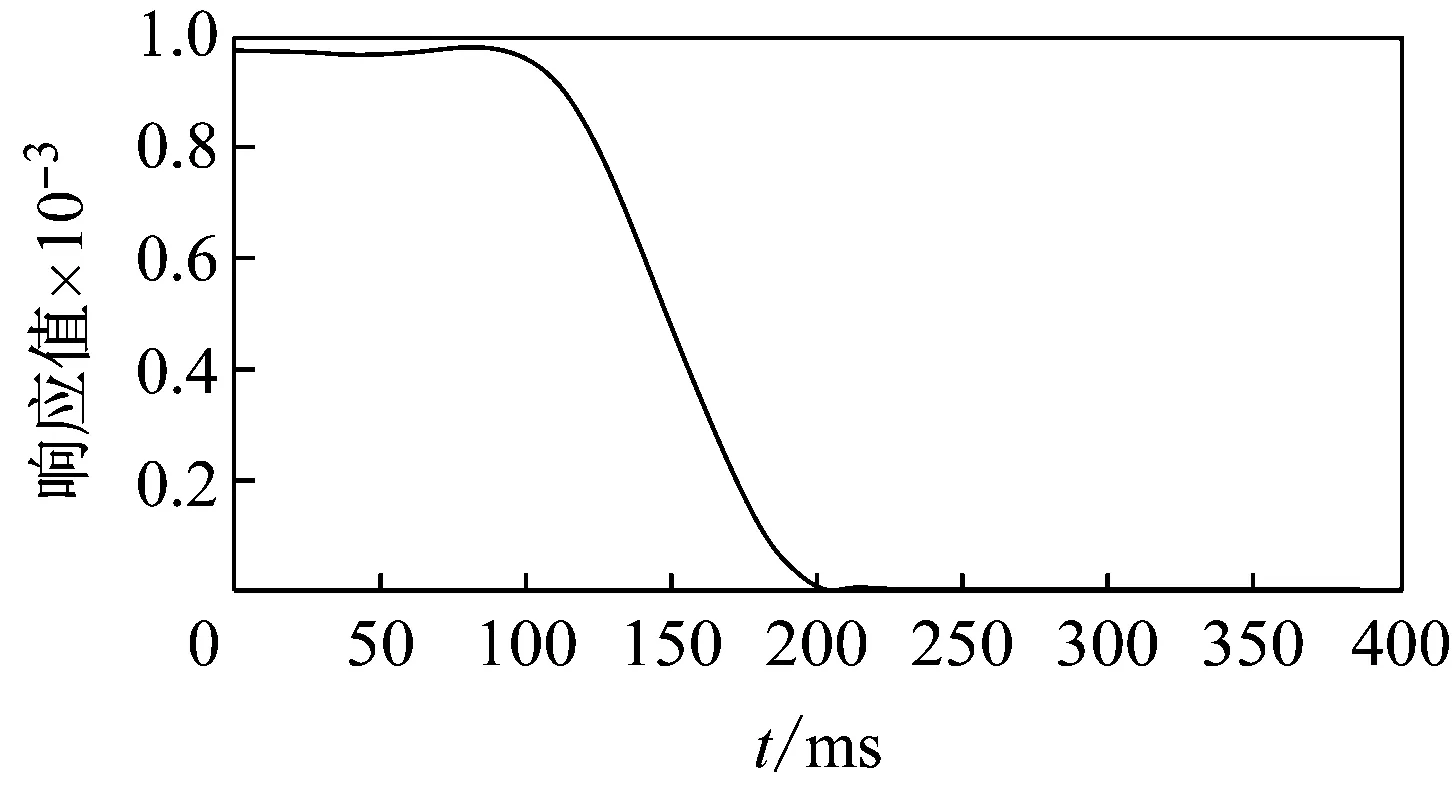
图6 滤波后频谱

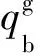
(8)

然后，利用向量的叉积，e可视为误差向量对机体坐标系的纠正，即：

θ=g·t+k·e

(9)

式中，k为一个常量系数。

再利用二阶毕卡法解四元数微分方程式(7)，更新四元数为下一次计算做准备。毕卡二阶算法为

(10)

式中：Δθ为角增量。

最后将四元数转化为欧拉角

Qθ=arcsin (-2q1q3+ 2q0q2)

Qr=arctan2(2q2q3+2q0q1-2q1q1-2q2q2+1)

Qψ=arctan2(2q1q2+2q0q3,-2q2q2-2q3q3+1)

通过以上算法成功得出了机械手的姿态角，角度误差满足了控制要求。姿态计算效果如图7～图9所示，图中实线是通过解算后的姿态角，虚线是解算前的姿态角。由图中数据可看出，解算的姿态角不仅能即时的反映角度变化且曲线平滑，说明姿态解算算法有效。

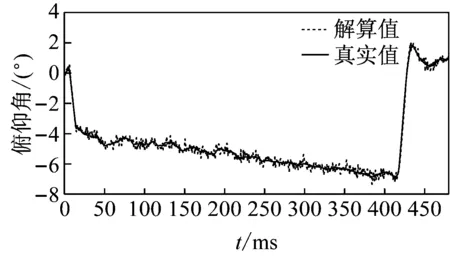
图7 俯仰角曲线图

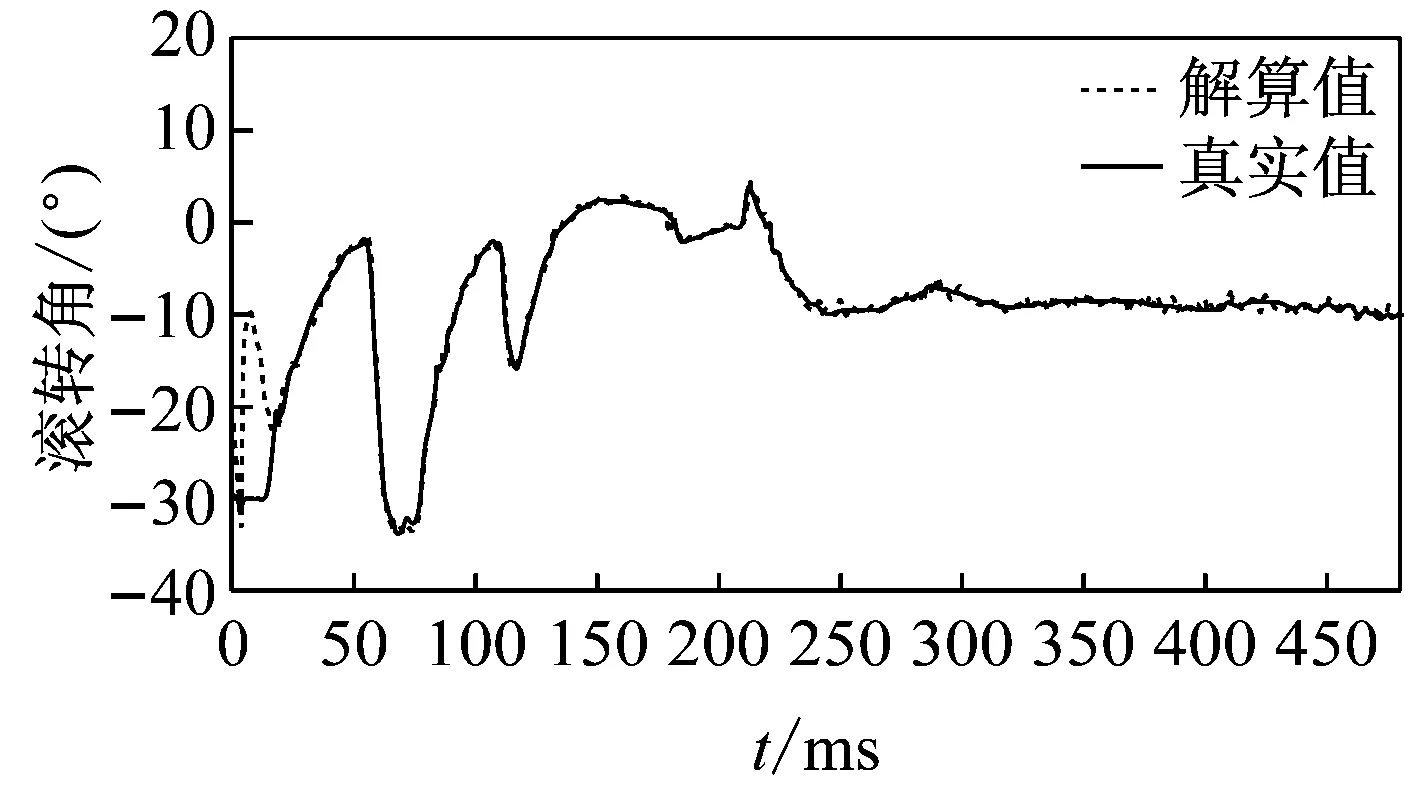
图8 滚转角曲线图

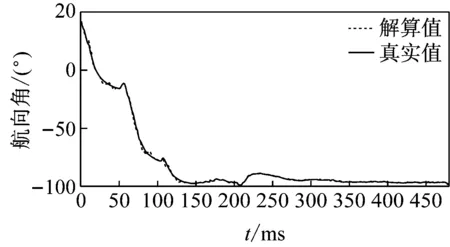
图9 偏转角曲线图

4 结 语

经实验表明，利用四元数互补滤波的方法进行姿态解算，角度误差均在±1°以内，满足控制要求。从上面解算仿真图可以看出解算的姿态角能即时反映出角度的变化，解算后的曲线更加平滑，说明姿态解算算法有效，显著提高了解算后的精度。本文采用的低通滤波器进行滤波对截止频率的选择有很高的要求，选择不当可能会导致实验结果的偏差。因此，接下来可以尝试采用融合算法进行滤波处理，提高滤波精度。

[1] 陈哲. 捷联惯导系统原理[M]. 北京：宇航出版社, 1986.

[2] 陈孟元, 谢义建, 陈跃东. 基于四元数改进型互补滤波的MEMS姿态解算[J]. 电子测量与仪器学报, 2015, 29(9):1391-1397.

[3] 孙金秋, 游有鹏, 傅忠云. 基于共轭梯度法和互补滤波相结合的姿态解算算法[J]. 传感技术学报, 2014(4):524-528.

[4] 汪绍华, 杨莹. 基于卡尔曼滤波的四旋翼飞行器姿态估计和控制算法研究[J]. 控制理论与应用, 2013, 30(9):1109-1115.

[5] 乔相伟, 周卫东, 吉宇人. 用四元数状态切换无迹卡尔曼曼滤滤波器估计的飞行器姿态[J]. 控制理论与应用, 2012, 29(1):97-103.

[6] 贺海鹏, 阎妍, 马良,等. 基于IEKF的四旋翼无人机姿态测量方法研究[J]. 计算机仿真, 2015, 32(4):56-60.

[7] 尹剑, 陈红, 杨萌,等. 捷联姿态计算中方向余弦与四元数法分析比较[J]. 兵器装备工程学报, 2015, 36(9):106-110.

[8] 刘辉邦, 褚金奎, 支炜,等. 基于STM32的无人机姿态测量系统设计[J]. 传感器与微系统, 2013, 32(8):108-110.

[9] 刘松国, 朱世强, 王宣银,等. 基于四元数和B样条的机械手平滑姿态规划器[J]. 浙江大学学报(工学版), 2009, 43(7):1192-1196.

[10] 刘星. 多维MEMS惯性传感器的姿态解算算法研究[D]. 哈尔滨：哈尔滨工程大学, 2013.

[11] 张栋, 焦嵩鸣, 刘延泉. 互补滤波和卡尔曼滤波的融合姿态解算方法[J]. 传感器与微系统, 2017, 36(3):62-65.

[12] 左国玉, 于双悦, 龚道雄. 遥操作护理机器人系统的操作者姿态解算方法研究[J]. 自动化学报, 2016, 42(12):1839-1848.

[13] 秦永元. 惯性导航[M]. 2版. 北京：科学出版社, 2014.

[14] 肖尚彬. 四元数方法及其应用[J]. 力学进展, 1993, 23(2):249-260.

[15] WANG Z H, CHEN X J, ZENG Q S. Comparison of strapdown inertial navigation algorithm based on rotation vector and dual quaternion[J]. Chinese Journal of Aeronautics, 2013, 26(2):442-448.