滑模观测器在无刷直流电动机无位置传感器直接转矩控制中的应用

贺 俊

(上海矩奉电动机自动化有限公司 技术部，上海 200331)

无刷直流电动机由于成本低廉和转矩密度高等优点，自19世纪70年代起，被广泛应用于工业领域。传统无刷直流电动机位置检测通常通过位置传感器实现，为了降低成本；同时，由于在高温、高压等应用场合下位置传感器存在易失效问题，无刷直流电动机的无位置传感器控制成为了目前研究的热点。传统的位置检测方法，在高功率等应用场合容易失效，且存在检测精度低、转矩波动大和控制性能差等问题，严重影响了无位置传感器控制的应用范围。直接转矩控制方法可以有效减小电动机的转矩波动，但对位置、转矩等反馈信号的精度要求较高，且由于控制结构复杂，在无位置传感器控制中应用较少，通常用于永磁同步电动机的控制中。本文基于电动机的扩展状态方程建立滑模观测器，研究精确估算转速、转矩和位置信号的算法，并简化直接转矩控制结构，使其适用于无刷直流电动机的转矩控制。

1 滑模控制基本原理

滑模观测器作为基于变结构控制观测器，具有对系统的参数、扰动不敏感、鲁棒性高等优点[1]。滑模观测器作为闭环观测器，把可以直接测量的物理量作为系统输入，根据状态方程设计观测器的结构，输出所需要观测的特定物理量[2]。在无刷直流电动机位置检测的应用中，可以通过检测电压、电流信号作为输入，利用滑模观测器精确估算电动机的反电势、速度和转子位置等运行参数[3-4]。

无刷直流电动机相反电势滑模观测器通常在两相静止α-β坐标系下建立，此时无刷直流电动机电压方程可表示为[5]

(1)

式中:iα，iβ为两相静止坐标系下α，β轴电流，A；L为相电感，H；R为相电阻，Ω；uα，uβ为两相静止坐标系下α，β轴相电压，V；eα，eβ为两相静止坐标系下α，β轴相反电势，V；ωr为电动机转子角速度，rad/s；θ为电角度,rad;ψf为永磁体磁链幅值，Wb。

无刷直流电动机的扩展状态方程为[6]

(2)

由扩展状态方程可以建立如下扩展状态滑模观测器

(3)

式中:n为对应物理量的估计值;Zα,Zβ为切换控制函数;m为比例系数。

切换函数选择Sigmoid函数，选择自适应律为

(4)

式中:kp，ki为PI控制器比例系数和积分系数。

扩展状态自适应滑模观测器控制如图1所示。

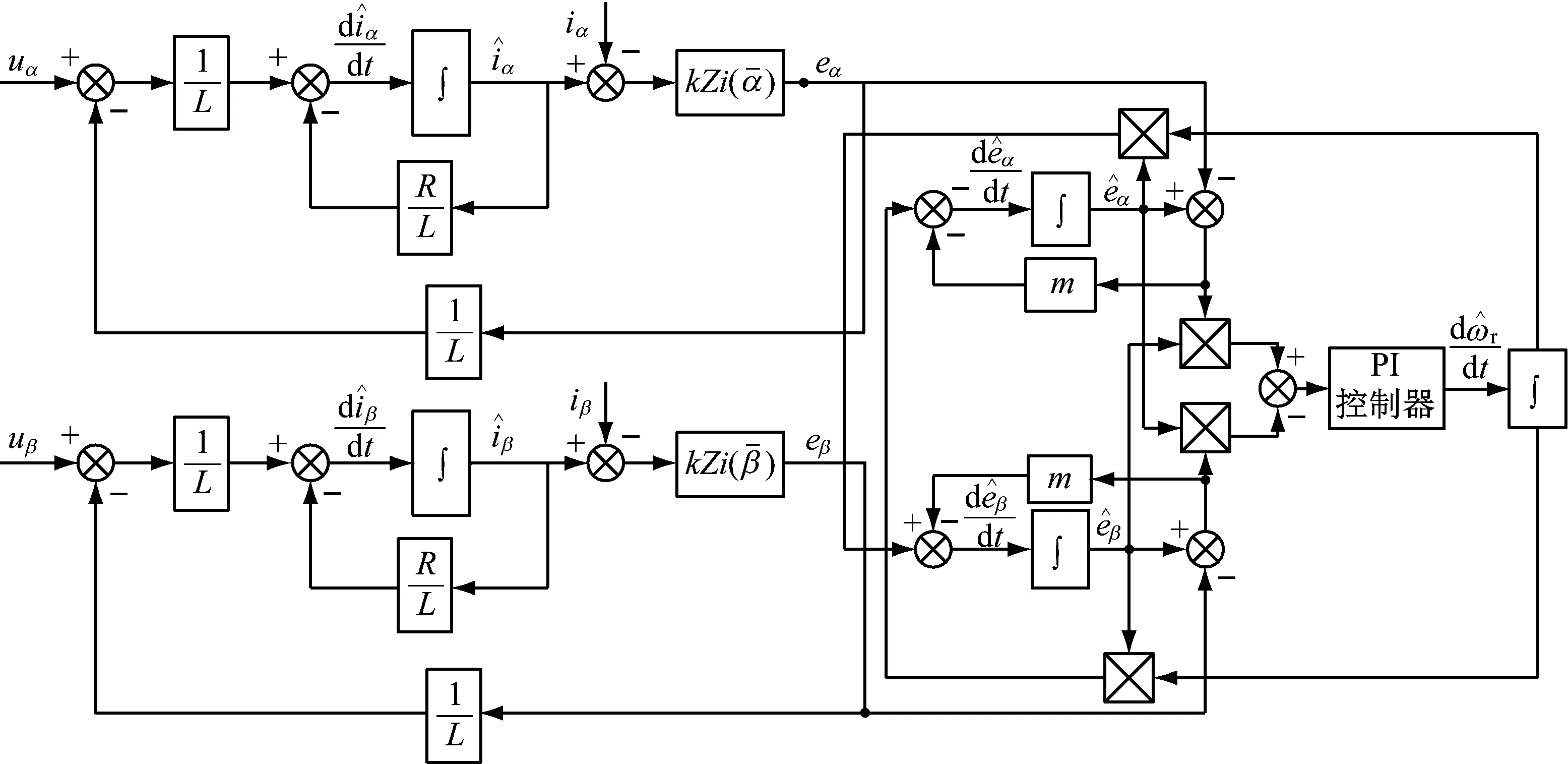
图1 扩展状态自适应滑模观测器控制框图

在实际的控制系统中，由于电动机的中点m一般不引出，导致相电压不能直接测量。因此，滑模观测器的输入电压信号不能直接测量[7]。图2为电压源控制的无刷直流电动机及其驱动系统等效电路[8]。

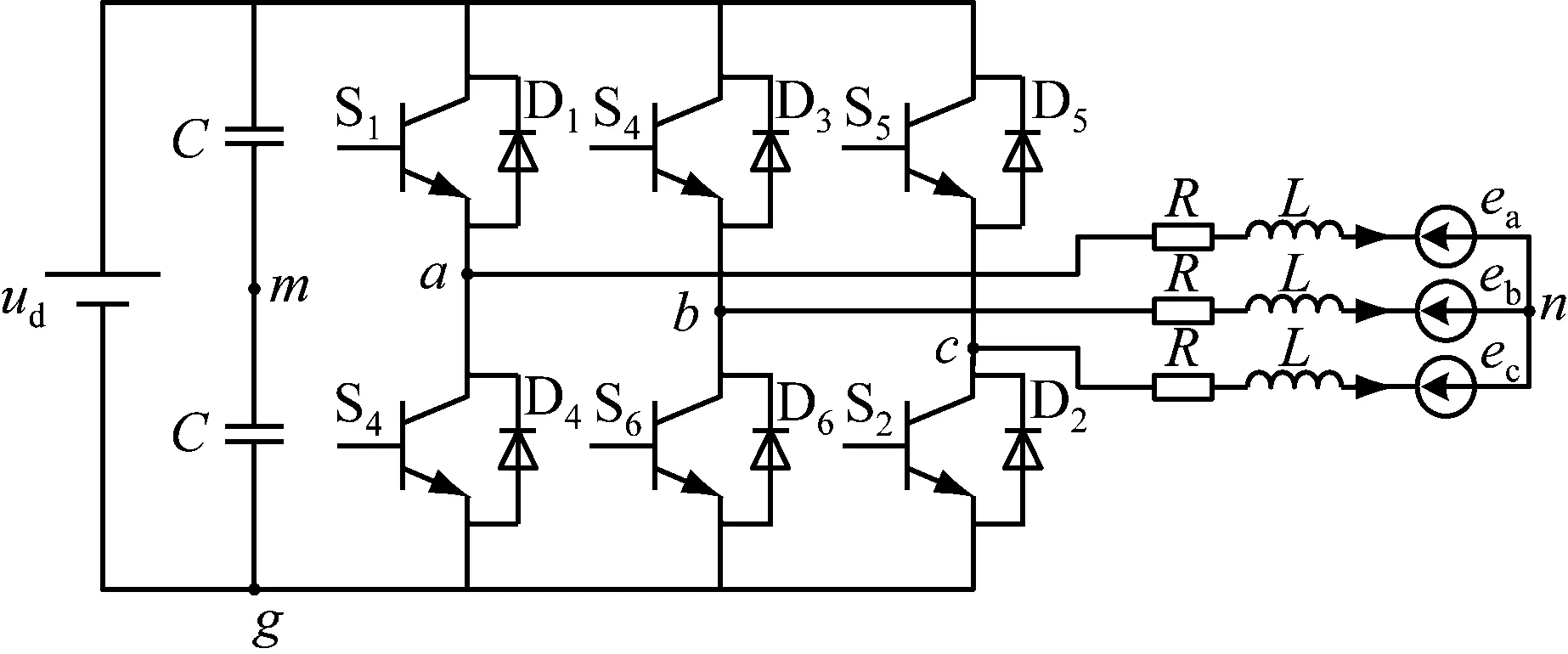
图2 无刷直流电动机与驱动系统等效电路图

由图2知，端电压uag，ubg，ucg是可以测得的，可通过下式求得[9]

(5)

估算得到精确的反电势值后，通过锁相环法得到位置信号，位置信号锁相环算法控制框图如图3所示。

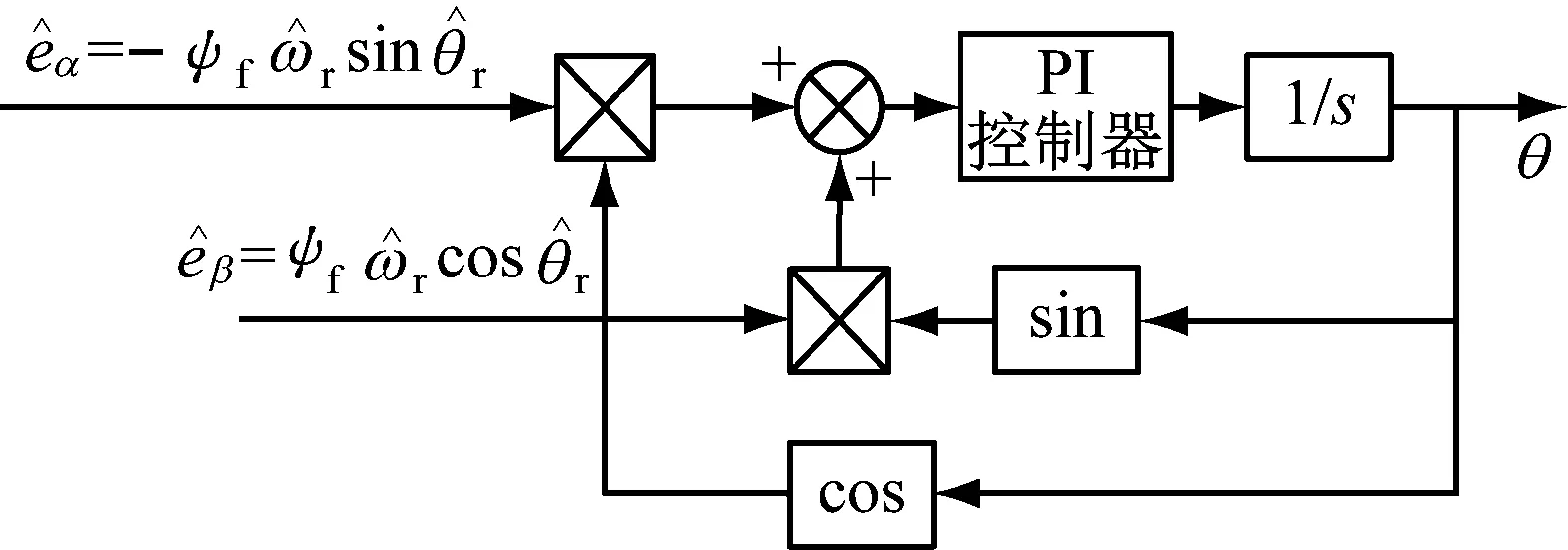
图3 位置信号锁相环算法控制框图

由式(1)可得

(6)

由转子角速度ωr可计算得出电动机转速。

2 无刷直流电动机直接转矩控制

无刷直流电动机直接转矩控制以转矩作为目标控制量，建立定子坐标下的电动机模型，控制定子磁链和转矩。反电势为正弦型的无刷直流电动机的电磁转矩，可以表示为[10]

Te=km|ψs||ψf|sinθ

(7)

式中:km为转矩系数;ψs为定子磁链空间矢量;ψf为转子磁链空间矢量;|ψs|为定子磁链幅值，Wb；|ψf|为转子磁链幅值，Wb；θ为ψs，ψf之间的夹角即磁通角,rad。

由于无刷直流电动机转子磁链不发生变化，如果固定定子磁链的幅值不变，根据式(7)可知电磁转矩将只受磁通角控制[11]。

若用Us表示电压空间矢量，则满足：

(8)

由于定子电阻较小，可以忽略定子电阻的影响,则有

(9)

对式(9)进行离散化，可得

ψs(k+1)=ψs(k+1)+Us(k)ΔT

(10)

式(10)表明，在每个采样周期内，通过施加合适的电压空间矢量，可以控制定子磁链矢量的运动轨迹[12]。

对于直流电压源三相全桥拓扑的驱动器，6个开关管的开关状态可以用一个6位的2进制数表示。其中，直通等组合在实际运行中是不允许的，其余任意一种有效的开关状态都对应了一种电压空间矢量[13]。电压矢量分布及扇区划分如图4所示。电压空间矢量选择如表1所示。有别于传统的6电压矢量控制，为了更精细地控制定子磁链[14]，如图4所示的扇区示意图是按照12个电压矢量划分的。假设某一时刻定子磁链矢量处于I扇区，规定逆时针方向为正，则在图4所示的12个电压空间矢量中，可以使得磁链旋转的电压矢量有多个，通常选择与扇区中线垂直的电压矢量。因此，若需磁链矢量向正方向旋转，则施加电压矢量U4；若需磁链矢量向反方向旋转，则施加电压矢量U10，以此类推。给定定子磁链幅值大于实际定子磁链幅值时，选择扇区符号为-1，此时应选择可以使定子磁链幅值减小的电压空间矢量，使得实际与给定定子磁链幅值之间的差值减小，否则相反。实际应用时，考虑到系统的稳定性，给定定子磁链幅值和实际定子磁链幅值的比较，应采用滞环比较。

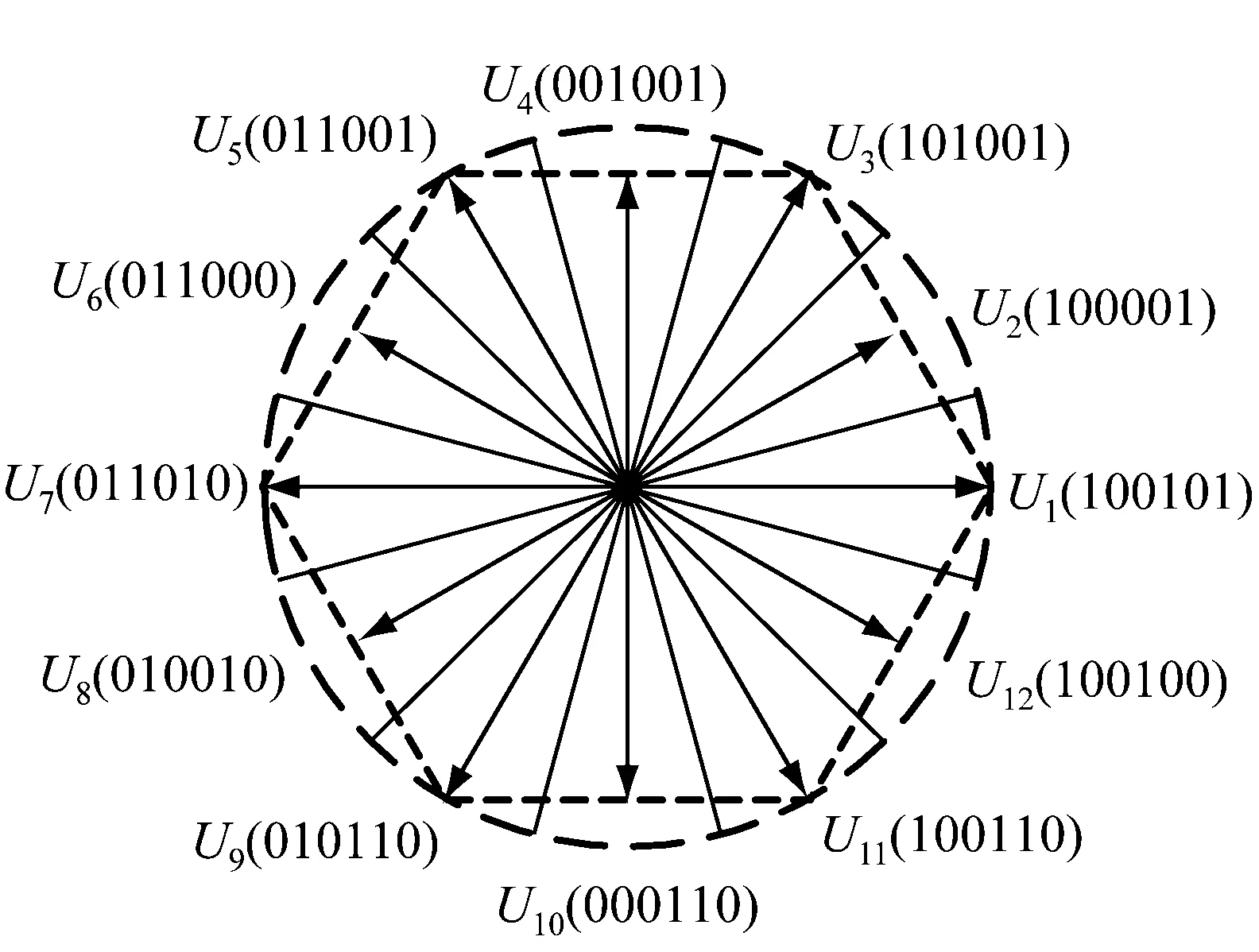
图4 电压矢量分布及扇区划分图

表1 电压空间矢量选择表

传统的直接转矩控制通常是双滞环结构[15]，如图5所示。式(9)是一个纯积分环节，若初始值不准确，会在积分结果中出现一个无法消除的直流分量，且控制结构也较为复杂[16]，在对磁链控制要求不严格的场合，可以采用简化控制方式，简化的直接转矩控制框图如图6所示。

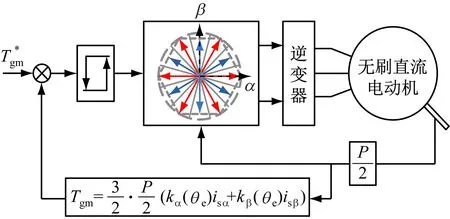
图6 简化的直接转矩控制框图

由电动机理论可知电动机电磁转矩还可以表示为

(11)

对于表贴式无刷直流电动机，交直轴电感值满足Ld0=Lq0=Ls，则式(11)可以简化为

(12)

由于

(13)

代入式(12)得

(14)

而定子磁链满足

(15)

且在两相静止坐标系α-β轴系下相电压方程为

(16)

将式(16)代入式(15)得

(17)

由于ψr=ψs-Lis，代入式(17)得

(18)

代入式(14)得

(19)

由式(19)可知，可以由相反电势、相电流及转速计算电磁转矩。本文前面已经研究了相反电势、转速的估算方法，相电流可以直接测得，所以电磁转矩是可准确估算的。

3 仿真模型

使用Simulink软件建立基于滑模观测器的无刷直流电动机无位置传感器直接转矩控制仿真模型。其中，直流电源电压为300 V，电动机相电阻R=2.875 Ω，相电感L=10 mH。

设定转速为500 r/min，电动机模型中可以引出三相反电势，与通过滑模观测器估算的相反电势进行比较。图7为转化到α轴的反电势波形图(实际值与滑模观测器的输出值对比)，图8是对图7的局部放大。

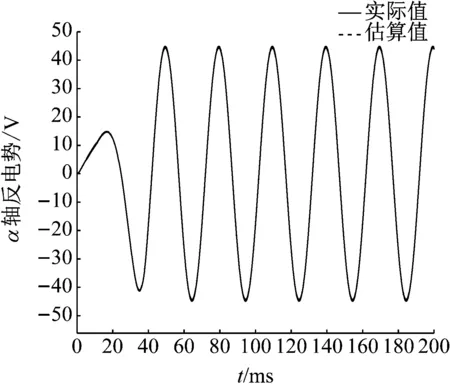
图7 相反电势波形图

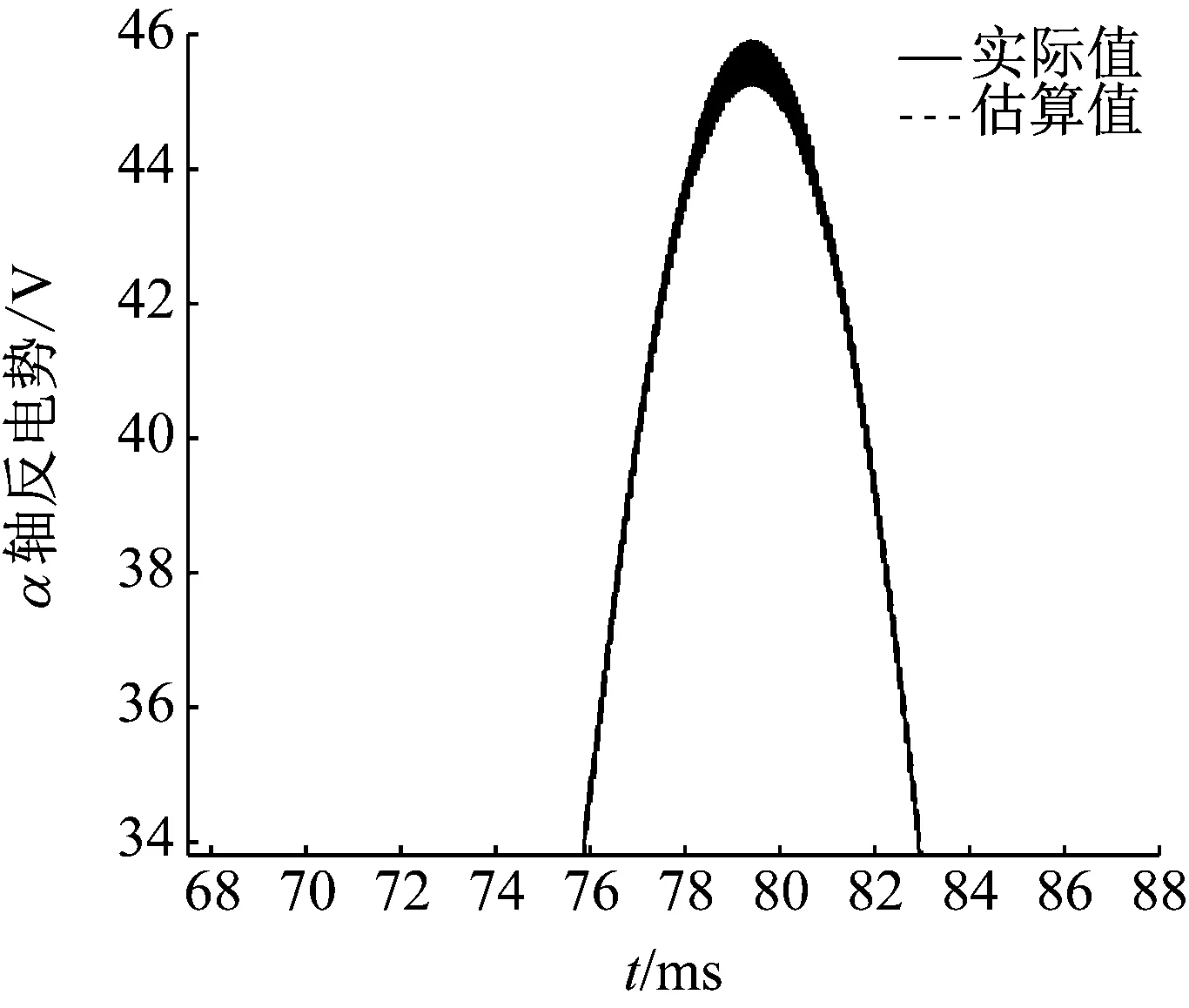
图8 相反电势波形局部放大图

由图7和图8可见，通过滑模观测器估算的相反电势与实际值误差很小。得到反电势后，进一步计算速度信号和位置信号(通过锁相环法)。图9为转速信号波形图(实际值和估算值对比)，图10为图9的局部放大，图11为转子位置信号波形图(实际值和估算值对比)。由此可见，通过滑模观测器和锁相环的方法，能准确快速地跟踪无刷直流电机运行时的反电势、转速和位置信号。

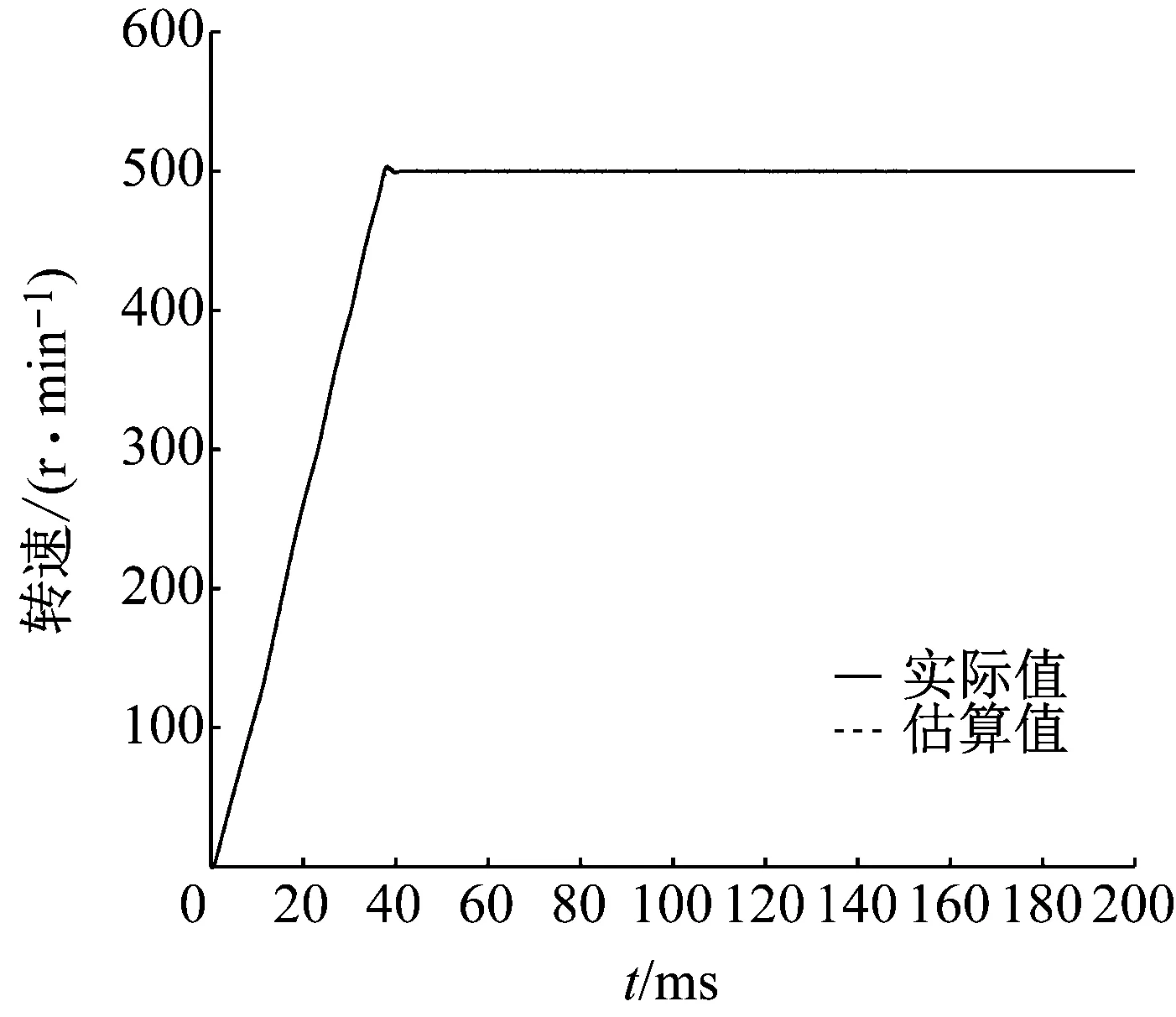
图9 速度信号波形图

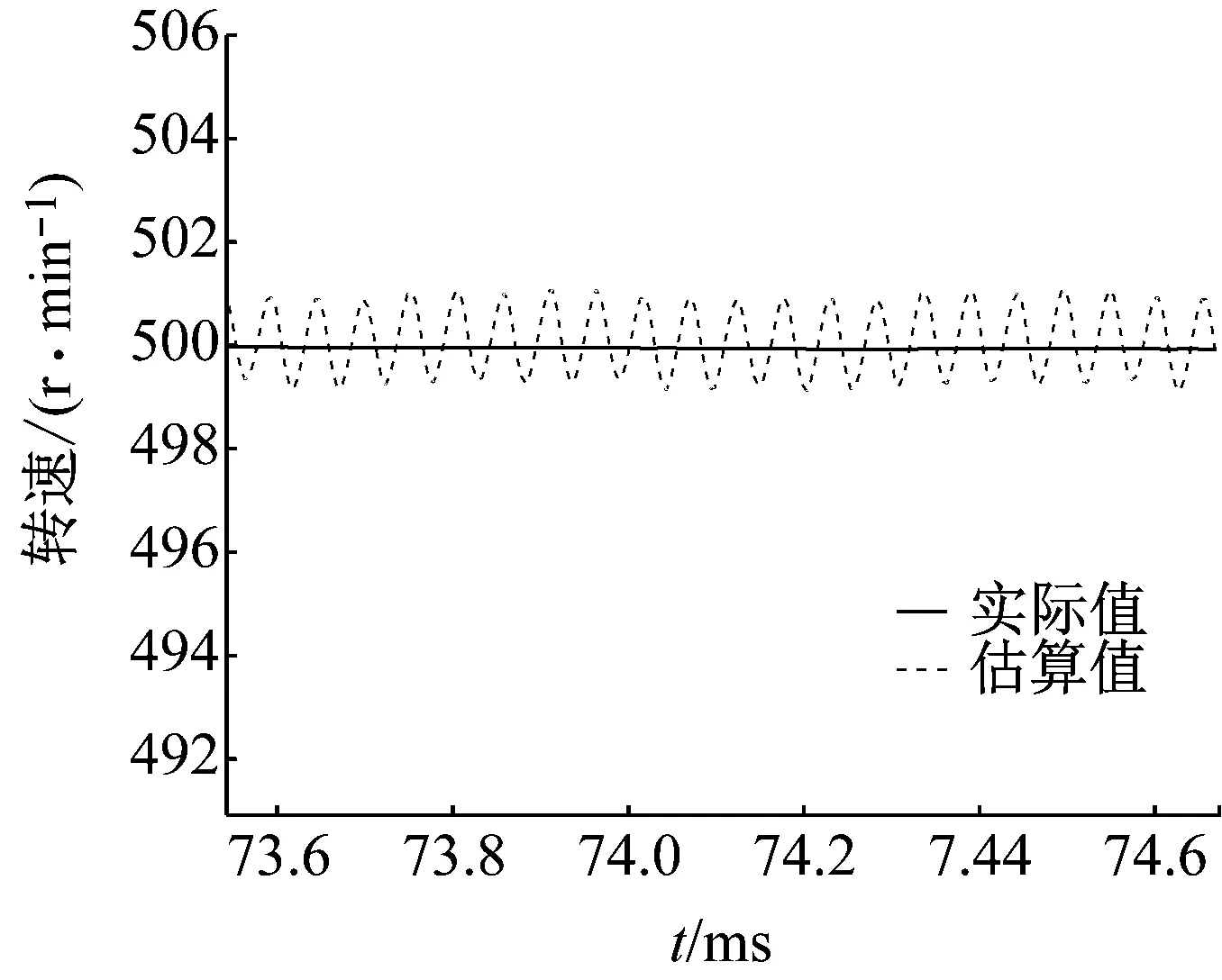
图10 速度信号局部放大图

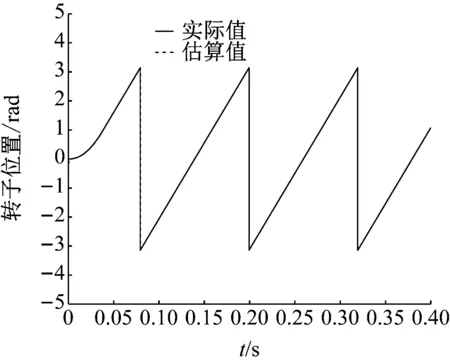
图11 转子位置信号波形图

在静止状态下，由于没有位置传感器，无刷直流电动机起动时初始位置无法确定，因此在起动时，人为地设置一组同步信号，假设为霍尔传感器的位置信号，并按一定频率按照设定转速方向改变位置信号。按此假定的位置信号施加电压矢量，电动机在此电压矢量作用下将会低速转动。

由以上的分析可知，滑模观测器和锁相环可以快速地跟踪反电势、位置信号和速度信号。因此，可以在较短时间后按照估算的位置信号进行控制。此外，由静止起动时，若不对电流进行控制，将产生很大的起动电流。本仿真模型中设定最大相电流瞬时值不超过±15 A，设定起动时负载转矩为5 N·m，转速给定为500 r/min， 0.1 s时转矩突变为10 N·m， 0.2 s时转速突变为1 000 r/min，采用直接转矩控制。图12为转速信号波形图，图13为三相电流信号波形图，图14为电磁转矩波形图。

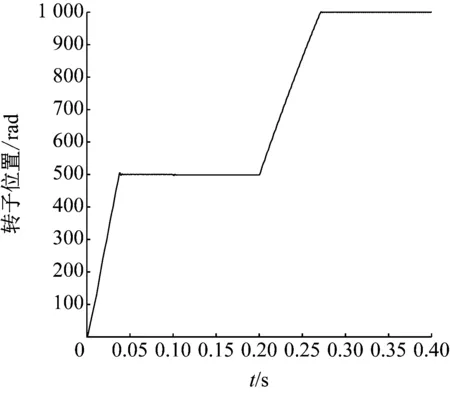
图12 速度信号波形图

可见采用直接转矩控制，三相电流最大值得到了有效的抑制，转速加速平稳且没有明显的超调，稳态时转矩波动较小，可见直接转矩控制对转速和转矩给定的阶跃信号响应迅速，电动机切换平稳。

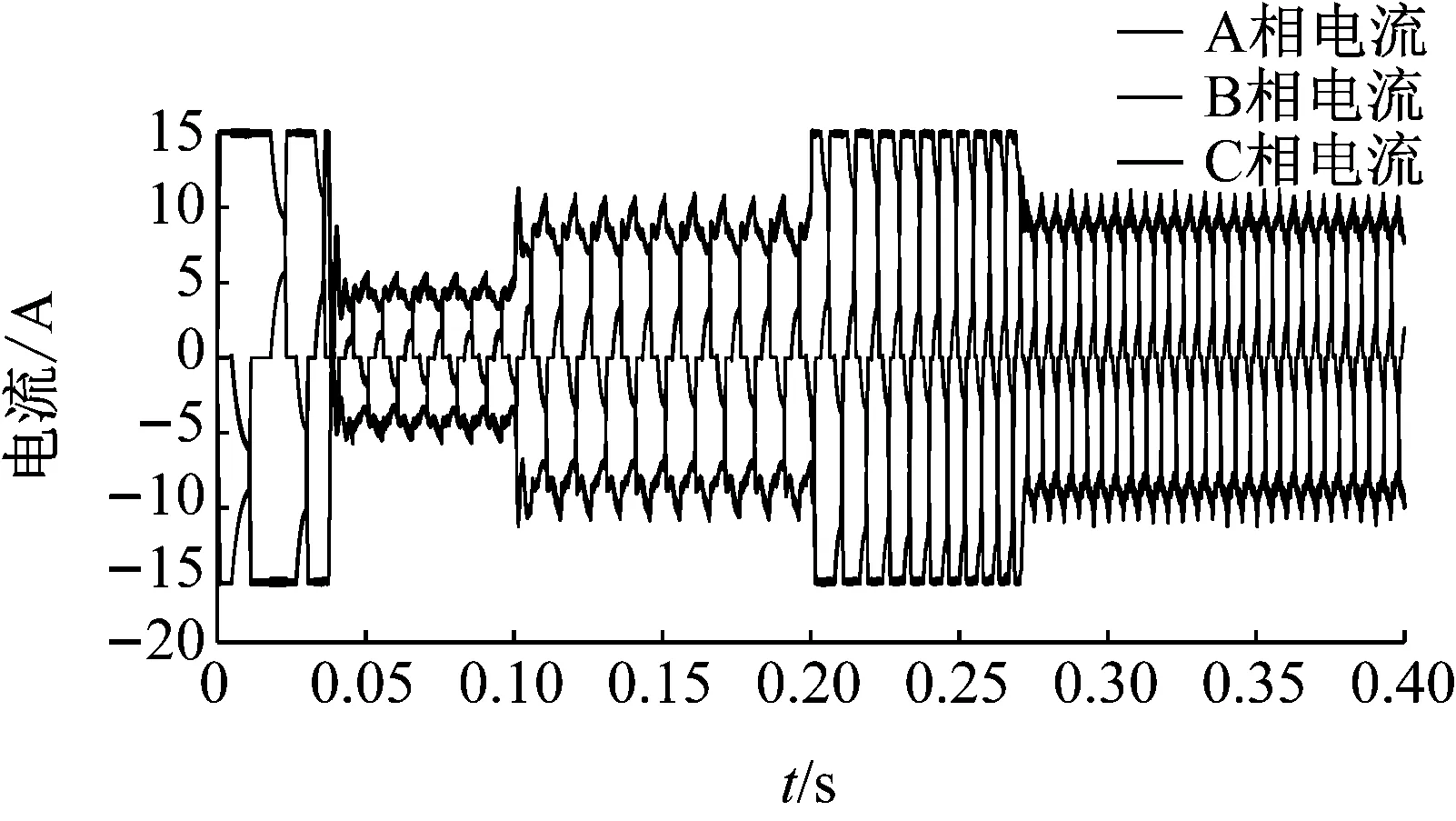
图13 三相电流波形图

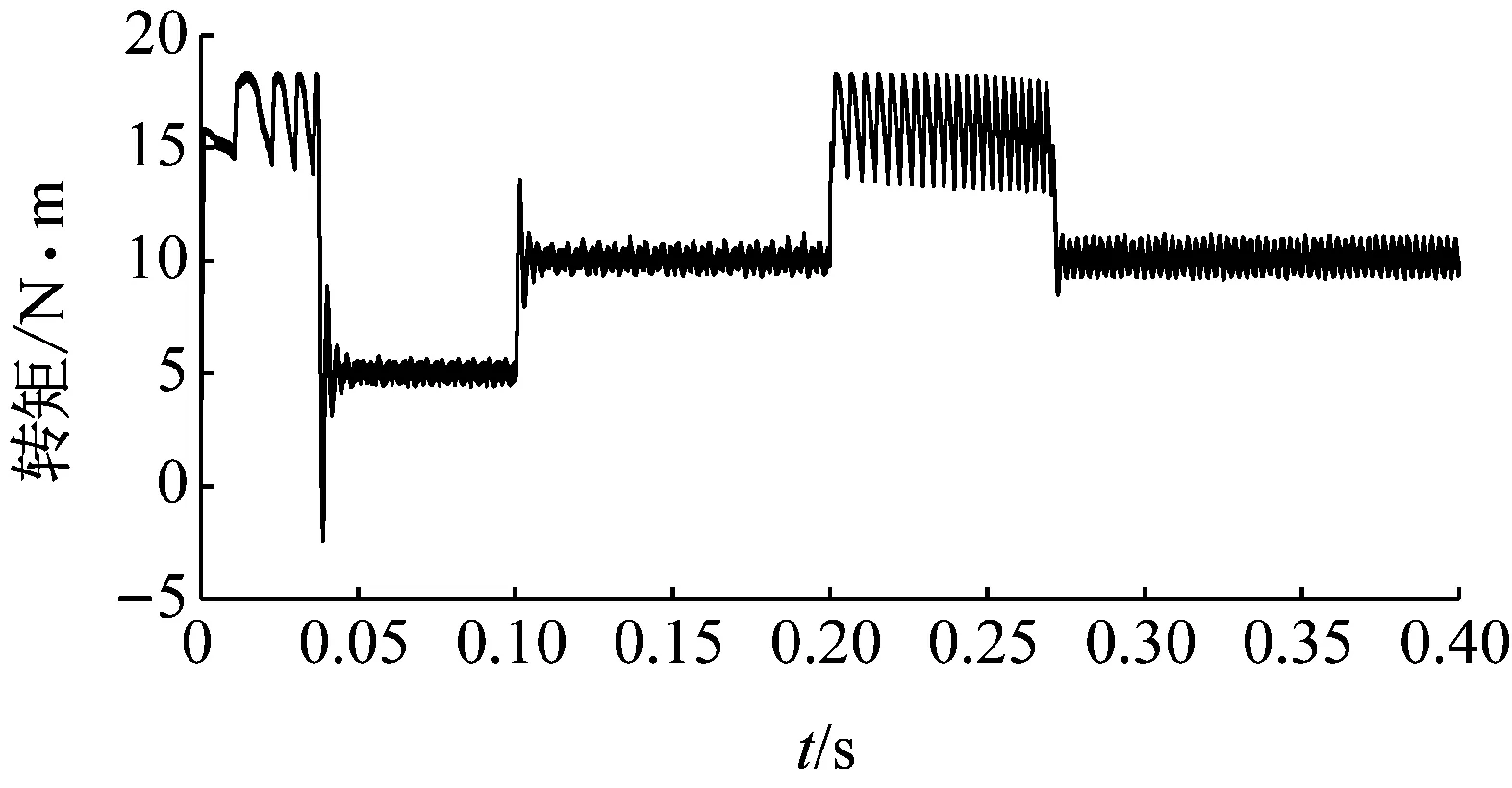
图14 电磁转矩波形图

4 结论

本文研究了滑模观测器在无刷直流电动机无位置传感器控制中的应用，通过无刷直流电动机的扩展状态方程，建立了滑模观测器，准确估算出了无刷直流电动机的相反电势。通过相反电势计算出电动机转速，并通过锁相环控制精确地估算出位置信号。在此基础上，本文进一步研究了基于12电压矢量的直接转矩控制，并在Matlab中建立了Simulink仿真模型。仿真结果表明，滑模观测器和锁相环方法估算的位置、速度信号精度很高，结果可以直接用于直接转矩无位置传感器控制，驱动器得到了有效的过流保护，给定信号发生阶跃时，在保证驱动器不过流的情况下，可以迅速平稳地跟踪给定信号。本文的研究结果对于提高无刷直流电动机无位置传感器控制的性能、电动机运行的平稳性等有重要的实践指导意义。

[1] 焦晓雷. 基于准滑模观测器的无刷直流电动机无位置传感器控制技术研究[D]. 长沙：中南大学, 2012.

[2] 丁佩剑. 基于滑模观测器的PMSM矢量控制系统的研究[D].成都：电子科技大学, 2013.

[3] CHEN M S, HWANG Y R，TOMIZUKA M. A state-dependent boundary layer design for sliding mode control [J]. IEEE Transactions on Automatic Control, 2002, 47(10): 1677-1681.

[4] 朱昊,肖曦,李永东. 永磁同步电动机转矩预测控制的磁链控制算法[J]. 中国电动机工程学报, 2010, 30(21): 86-90.

[5] 朱光起. 基于十二拍控制模式的无刷直流电动机速度控制策略研究[D].哈尔滨：哈尔滨工业大学, 2013.

[6] LIU Y, ZHU Z Q, HOWE D. Commutation-torque-ripple minimization in direct-torque-controlled PM brushless DC drives[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 1012-2021.

[7] Saied M H, Mostafa M Z, Abdel-Moneim T M, et al. On three-phase six-switches voltage source inverter: a 150° Conduction Mode[C]//IEEE. Conference on Control & Automation.[s.l.]:[s.n.], 2006: 153-158

[8] WANG C M, WANG S J, LIN S K, et al. A novel twelve-step sensorless drive scheme for a brushless DC motor[J]. IEEE Transactions on Magnetics, 2007, 43(6): 2555-2557.

[9] NAM K Y, LEE W T, LEE C M, et al. Reducing torque ripple of brushless DC motor by varying input voltage[J]. IEEE Transactions on Magnetics, 2006, 42(4): 1307-1310.

[10] KIM D K, LEE K W, KWON B I. Commutation torque ripple reduction in a position sensorless brushless DC motor drive[J]. IEEE Transactions on Power Electronics, 2006, 21(6): 1762-1768.

[11] LIU Y, ZHU Z Q, HOWE D. Commutation-torque-ripple minimization in direct-torque-controlled PM brushless DC drives[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 1012-2021.

[12] SHI T N, GUO Y T, SONG P, et al. A New Approach of Minimizing Commutation Torque Ripple for Brushless DC Motor Based on DC-DC Converter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3483-3490.

[13] 李自成. 无刷直流电动机无位置传感器控制关键技术研究[D]. 武汉：华中科技大学, 2010.

[14] 刘均华. 永磁无刷直流电动机滑模变结构控制[D].天津：天津大学, 2005.

[15] 卢娜. 基于自适应滑模观测器的无刷直流电动机无位置传感器控制[D].天津：天津大学, 2008.

[16] 朱昊,肖曦,李永东. 永磁同步电动机转矩预测控制的磁链控制算法[J]. 中国电动机工程学报, 2010,30(21): 86-90.