基于W-M分形函数的三维粗糙表面摩擦生热研究

,,,,,

(大连交通大学 机械工程学院,辽宁 大连 116028)

大功率风电制动器具有制动转速高、制动力矩大的特点,其制动过程中大部分动能通过摩擦作用转化为热能,制动器摩擦副表面将产生大量摩擦热.制动闸片由于局部高温和应力集中的原因，材料属性发生改变,造成闸片不均匀摩擦损耗的加剧,影响了风电制动器的制动性能,并降低了制动闸片材料的利用率,因此,如能对制动过程中摩擦接触的微观过程进行深入研究,即可有效预测摩擦副接触表面的力-热分布状态,进而为改善制动摩擦副的工作性能,提高制动闸片的使用寿命提供理论依据.

制动过程中制动盘与闸片接触表面的摩擦接触,其微观实质是两个粗糙表面上一系列不规则微凸体的相互接触过程.实际滑动摩擦过程中,由于真实接触面积远小于名义接触面积且不连续,造成摩擦副间很小的真实接触面积上承担很大的实际载荷,接触微凸体将发生弹塑性变形,并形成“热点”[1].这些“热点”就是制动摩擦副的局部闪温.局部温度过高,及由此导致的摩擦副材料属性变化会引起两接触表面状态的变化.粗糙表面之间的滑动摩擦实质上是一个复杂的非线性接触问题.粗糙表面的形貌和接触特性对制动过程摩擦、磨损和传热都有着重要的影响.因此,研究粗糙表面轮廓形貌以及其对滑动摩擦中的温度与应力的影响有重要的应用价值.

一直以来,国内外学者就粗糙表面轮廓形貌进行了表征，并对其接触摩擦的过程进行了大量的研究.Archard[2]在其研究中首先体现出了分形的思想,将多尺度粗糙表面看作较大尺度的球形微凸体上承载了一簇较小尺度的球形微凸体.Mandelbort[3]首先提出了分形这一概念,并创立了分形几何学,用于解释那些不规则的、破碎的、参差不齐的和断裂的形状;其次在Weierstrass函数的基础上,提出了一种分形曲线函数的表达式,称为Weierstrass-Mandelbrot分形函数(简称W-M分形函数).Mandelbort提出的分形理论被逐渐应用到摩擦学的研究中.Bhushan[4]基于W-M分形函数提出了M-B分形模型,用W-M分形函数来模拟粗糙表面的轮廓线,把模拟两粗糙表面的接触简化为一等效粗糙表面与一理想刚性光滑平面的接触,提出了分形接触模型.葛世荣等[5]研究了通过磨削、车削等加工方法得到的表面轮廓曲线,发现粗糙表面具有明显的分形特征,提出分形维数与表面粗糙度之间呈负指数关系,并定义了特征粗糙度这一概念.魏龙等[6]考虑微凸体的变形特征和摩擦作用的影响，建立了滑动摩擦表面的分形接触模型,采用一个三次多项式来表达弹塑性变形微凸体的接触压力与接触面积的关系,并推导出不同临界条件下微凸体的真实接触面积.邓可月等[7]利用分形理论对表面形貌的分形特点进行研究,在建立W-M分形函数模型的前提下，对表面轮廓形貌进行二维及三维的模拟仿真分析,得出分形维数是影响表面轮廓曲面形貌的主要参数.韩传军等[8]建立了一个含球形微凸体粗糙表面与理想平面的滑动接触模型,探究了特定形状微凸体在摩擦过程中的应力与温度变化规律.本文基于W-M分形理论建立粗糙面微接触的滑动计算模型,将两个粗糙表面简化为一个分形粗糙表面与一个光滑平面的组合,建立粗糙面的滑动接触有限元计算模型,结合大功率风电制动器高速重载的制动工况,在不同分形维数、相对运动速度及施加载荷的边界条件下,模拟并分析了制动过程中粗糙表面的摩擦生热及热应力变化规律.分析结果为进一步研究制动过程中微观摩擦机理研究、粗糙表面摩擦副的闪点温度、摩擦副接触表面的力-热分布状态提供了参考依据.

1 基于W-M分形函数的粗糙表面模型建立

W-M分形函数可以准确地模拟和重构具有分形特性的分形表面,且处处连续但不可微,其本身具有自相似性,是用于表示随机轮廓的一种典型函数[9].其适用于工程表面的数学模型表达式为

(1)

式中:Z(x)为随机表面形貌的高度;x为轮廓的位置坐标;D为分形维数,它描述函数Z(x)在所有尺度上的不规则性;G为特征尺度系数,它反映Z(x)幅值大小,并决定Z(x)的具体尺寸；γ为轮廓的空间频率，对于服从正态分布的随机轮廓,为适用于高频谱密度及相位的随机性,一般γ的取值为1.5.基于W-M分形函数的三维分形表面的函数模型为

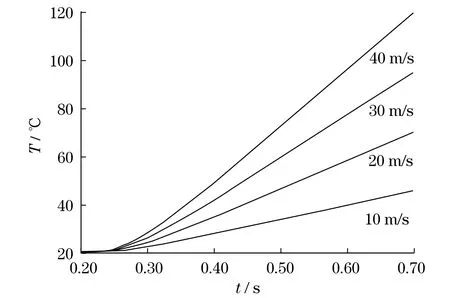
ysinBn)+An] (2

(2)

式中:Cn为尺度系数，是服从均值为0、方差为1的正态分布的随机数;An与Bn为相互独立且服从[0,2π]均匀分布的随机数;Ds为理论分形维数;n为自然序列数.

以W-M分形函数公式为理论基础,借助Matlab软件进行编程,在固定某些特定参数的条件下,对分形维数进行变换,模拟出不同分形维数下的粗糙表面形貌,如图1所示.固定参数中尺度系数取定值C=0.01,自然序列数为n=1,2,…,100.在选取横纵坐标x,y时,由于分形函数公式的特性,要求x≠0,y≠0.因此，横纵坐标的选取区间定在区间[1, 2]内.在区间内,x方向与y方向上每间距0.04上取一个点,取样点的数量为x方向和y方向各26个,总采样点数为676个；再根据An和Bn的两个随机数,求出每个采样点的z坐标值,进行样条拟合并最终绘制出三维状态下不同分形维数的微观表面轮廓形貌.

图1 不同分形维数三维粗糙表面轮廓形貌Fig.1 Three-dimensional rough surface profile topography at different fractal dimension

图1(a)～图1(e)分别为分形维数2.1,2.3,2.5,2.7和2.9时获得的三维粗糙表面轮廓形貌.从图1可以看出,粗糙表面轮廓曲面具有不规则性,呈现出高低不平的形状,不同分形维数下的曲面凹凸程度差别较明显,不仅显露出了轮廓形状的随机性,还体现出了表面形貌的复杂性.随着分形维数值的逐渐增大,粗糙表面轮廓形貌趋于复杂化,表面凹凸程度趋于密集化,且高度幅值变化频率也越来越快,这说明了分形维数是影响表面轮廓曲面形貌的主要参数,这为通过改变分形维数建立不同粗糙程度的摩擦表面模型提供了理论依据.

2 摩擦生热有限元模型的建立

2.1 三维粗糙表面模型的建立

由于粗糙表面轮廓形貌的不规则性,若将此三维模型直接用于有限元模拟,不仅需要增加网格数量导致运算量显著上升,而且很容易造成接触分析不收敛的情况,因此，需要对粗糙表面轮廓进行光滑处理.运用Matlab中的样条拟合功能,将分形粗糙表面轮廓拟合成光滑表面轮廓形貌,拟合后表面形貌的凹凸程度趋势并没有发生太大改变,但表面光滑程度较高,适合三维模型的建立和有限元仿真.选取其中一组分形维数Ds=2.7的三维粗糙表面轮廓,将其拟合后的表面各点数据导入到Creo中生成三维模型,粗糙体表面的轮廓形貌如图2所示.

图2 拟合后分形维数Ds=2.7的粗糙表面三维模型Fig.2 Three-dimensional model of rough surface with Ds=2.7 fractal dimension after fitting

2.2 边界条件与有限元计算模型

2.2.1热边界条件

在有限元接触分析的设定中,接触面单元不能穿透目标面,而目标面单元可以穿透接触面,且目标面一般选择标准为平面、网格较粗和面积较大的面,而接触面一般都选择硬度偏软的面.根据这一性质,选择制动盘为光滑表面作为目标面,而制动闸片为粗糙表面作为接触面.在制动过程中,摩擦生热产生的能量为

(3)

式中:FH是摩擦耗散能转换成能量的比例系数,当认为摩擦全部转化为热量的情况下，FH的值为1;τ为等效摩擦应力;v为滑动率.分配在接触面和目标面的摩擦生热能量分别为qc和qt,即

(4)

式中:FW为接触面与目标面之间的热量分配权重因子,qc和qt的关系为

(5)

式中:ρc,ρt分别为接触面和目标面的密度;Cc,Ct分别为接触面和目标面的比热容;kc,kt分别为接触面和目标面的热导率[10].在代入制动盘(目标面)和制动闸片(接触面)材料属性计算得热分配系数分别为31%和69%.

在制动过程接触的热边界条件中，热传导占主导地位,摩擦接触区域温度Tc=Tt,其中，接触面和目标面中，接触部分的热传导方程为

(6)

接触面与目标面未接触部分主要的热边界条件为热对流,其中，接触面和目标面的非接触部分的热对流方程为

(7)

式中:Tα为流体介质的温度,即刚接触时空气的温度;h12为接触面与流体介质的对流换热系数;h13为目标面与流体介质的对流换热系数.经计算,将对流换热系数设定为13.35 N·m/(h·km2).

2.2.2有限元计算模型

为简化模型,提高分析效率,对摩擦生热模型作如下基本假设:① 两摩擦件的材料组成均匀,且各向同性;② 制动闸片材料(铜基粉末冶金)和制动盘材料(Q345-B)的密度、比热、热导率、热膨胀系数、弹性模量、泊松比等各项物理参数均为常数,且不受温度变化影响;③ 由于滑动过程时间极短,因此，仅考虑热传导和热对流的影响,忽略热辐射的作用;④ 忽略粗糙表面的磨损及其影响,认为动能完全转化为摩擦热而被摩擦副吸收;⑤ 摩擦过程中,符合库仑摩擦定律,摩擦系数保持不变.两摩擦件材料的热物理参数如表1所示.

表1 摩擦件材料物理参数Tab.1 Friction material physical parameters

为简化运算,制动盘和制动闸片均采用局部模型,对两者的三维模型进行网格划分,划分后的有限元模型如图3所示.图3中:上方模型为分形粗糙表面采用四面体单元划分网格,共计有19 392个四面体单元(C3D4T);下方模型为光滑表面,理想光滑平面体外形规则,为减少运算量,选用六面体单元(C3D8T)划分网格,共计有9 600个六面体单元.由于接触计算及弹塑性计算的复杂性,考虑到计算成本,滑动距离为L=20 mm.运动过程分为2个阶段:第1阶段在分形表面上施加载荷,使分形粗糙表面往下运动,挤压光滑表面,在光滑表面的底面限制Z方向自由度,并对粗糙体的侧表面分别施加法向约束;第2阶段对光滑平面分别施加不同的速度载荷.

图3 制动过程分形粗糙体与光滑表面有限元模型Fig.3 Finite element model of fractal aperture and smooth surface in braking process

3 摩擦生热仿真结果分析

制动过程中,各种因素共同作用影响摩擦生热.为探究不同因素各自对于摩擦生热的影响程度,在保证其他参数不变的情况下,分别改变单一变量以研究其对制动过程中摩擦生热的影响.因此，选取不同分形维数、滑动速度以及施加载荷的条件，对制动过程分形粗糙表面的摩擦生热进行探究,结合大功率风电制动器制动的实际工况,选取分形维数Ds分别为2.1,2.3,2.5和2.7,运动速度v分别为10,20,30和40 m/s,施加载荷P分别为10,20,30和40 MPa,以探究不同单一变量变化对分形粗糙表面摩擦生热的影响.

3.1 分形维数对摩擦生热的影响分析

图4(a)～图4(d)分别是施加载荷为30 MPa时,分形维数Ds为2.1,2.3,2.5和2.7不同情况下，摩擦初期的表面热区分布形貌图.图4(a)为分形维数Ds=2.1时的温度分布云图,从图中可以看出其热区分布形式主要以块状热区为主,点状热区的数量仅占极少数,而在制动初期其最大闪点温度为146.7 ℃.图4(b)为分形维数Ds=2.3时的温度分布云图,相较于图4(a)其块状热区的数量有所减少,而点状热区的数量呈增长的趋势,其制动初期的最大闪点温度为200.7 ℃.图4(c)为分形维数Ds=2.5时的温度分布云图,块状热区的接触面积与数量都有大幅度减少,而点状热区的数量也超过了块状热区的数量.其制动初期的最大闪点温度为276.2 ℃.图4(d)为分形维数Ds=2.7时的温度分布云图,其热区基本上都为点状热区,而制动初期的最大闪点温度为317.0 ℃.从图4的温度分布云图可以分析出,当分形维数较小时,摩擦初期形成的热区以块状热区居多,而点状热区的数量偏少,随着分形维数的增大,点状热区的数量增多,而块状热区的数量减少,形成这种趋势的原因是当分形维数较小时,表面形貌复杂程度低,分形粗糙表面单位面积内的波峰波谷数量也较少,表面更为平坦,因此，更容易形成块状热区.而随着分形维数增大,表面形貌的复杂程度也随之上升,表面凹凸程度趋于密集化,使得单位面积内的波峰波谷数量也随之增加,点状热区形成的概率随之增大.此外,随着分形维数增大,粗糙体接触界面的最高温度也呈现上升趋势.这是因为分形维数较小时,接触部分大多是面接触,接触部分最大接触压力较小,因此，摩擦初期摩擦生热的最大温度值较小;当分形维数较大时,面接触部分减少,点接触部分增加,导致最大接触压力值也随之增大,其接触的微凸体的最大闪点温度也随之升高.由图4还可看出,虽然分形粗糙曲面在构造时就具有随机性的特点,导致摩擦生热形成的热区分布趋势也存在着一定的随机性,但分形维数数值的变化还是会对摩擦生热产生较大影响.

图4 不同分形维数情况下粗糙表面热区分布图Fig.4 Rough surface hot zone distribution at different fractal dimension

3.2 运动速度对摩擦生热的影响分析

图5为不同相对运动速度下,滑动时间为500 μs内的分形粗糙表面最顶端微凸体节点(节点814)的温度随时间变化历程图.由图5可以发现,在制动过程中,温度随着时间的变化呈上升趋势.根据温度曲线变化的趋势,可以将其分为2个阶段:第1个阶段(0～20 μs)为急剧增长阶段；第2阶段(20～500 μs)为缓慢增长阶段.从图5中可以看出,相对运动速度越高,急剧增长阶段微凸体的温升就越大,缓慢增长阶段微凸体的最高温度值也越大.当速度分别为10,20,30和40 m/s时,粗糙峰最大温度分别为215.295 ℃,388.176 ℃,539.303 ℃和691.053 ℃.

图5 分形粗糙体最高微凸体(节点814)温度-时间曲线图Fig.5 Temperature-time curve of highest asperity (Node 814) in fractal aperture

不同相对运动速度下,粗糙体非接触面区域节点(节点504)温度-时间变化曲线如图6所示.由图6可见,非接触节点的温度随着制动时间的推进，呈近似线性增长的趋势.当相对运动速度越大时,曲线的斜率也越大,这是因为速度越快微凸体的最高温度越大,微凸体与非接触部分温差越大,导致非接触面区域的热传递速率越快,其结论也完全符合傅里叶定律.

3.3 施加载荷对摩擦生热的影响分析

图7(a)～图7(d)分别是运动速度为20 m/s,分形维数Ds=2.7条件下,施加载荷为10,20,30和40 MPa的分形粗糙表面接触压力云图.从图7(a)中可以看出,当施加载荷为10 MPa时,加载后的制动初期最大接触压力为1 588 MPa,实际接触点的数量为7个.在图7(b)中,施加载荷为20 MPa,加载后的制动初期最大接触压力为1 714 MPa,实际接触点较图7(a)有所增加,其数量大约为14个.在图7(c)中,加载后的制动初期最大接触压力为1 653 MPa,实际接触点较图7(b)有小幅增加,其数量大约为18个左右.图7(d)为施加载荷为40 MPa的接触压力云图,其在加载后的制动初期最大接触压力为1 564 MPa,实际接触点数量在26个左右.根据图7可以看出:当施加的载荷越大,真实的接触面积越大,接触点数量越多,但接触点数量呈非线性增长趋势;且实际接触点的接触压力远大于施加载荷,最大接触压力数值处于1 600 MPa左右;随着施加载荷的增加,表面最大接触压力出现了一定程度起伏的情况,造成此情况的原因是真实的粗糙表面形状具有随机性与不规则性,使得接触面积并不是随着载荷增大而等比例的增大,这就导致接触压力并不随载荷增大而增大,而是在表面最大接触压力附近小幅波动.

图6 分形粗糙体非接触面(节点504)温度-时间曲线图Fig.6 Temperature-time curve of non-contact surface (Node 504)in fractal aperture

图8(a)～图8(d)分别是施加载荷为10,20,30和40 MPa的分形粗糙表面的温度云图.从图8(a)中可以看出,当施加载荷P=10 MPa在制动过程结束时,其最大闪温为443.7 ℃,并形成以最高闪温点为中心的一整块热区,且温度梯度的趋势明显.在图8(b)中，当施加载荷P=20 MPa时,相较于图8(a)其热区的范围有所扩张,热区数量也有一定增幅,其制动末期的最大闪点温度为456.0 ℃.在图8(c)中,施加载荷后热区的接触面积与数量都有一定量的增加,其制动末期的最大闪点温度为453 ℃.图8(d)为施加载荷P=40 MPa时的温度分布云图,可以看出,在制动末期热区数量的分布范围广且密集,且不少独立热区在最后合并成了整块热区,其最大闪温为454.1 ℃.从图8中可以看出,当施加载荷越大时,真实接触面积随之增大,在摩擦过程中,形成的热区数量越多,随着时间的推移,热区的面积也逐渐扩张.但在不同载荷作用下,其微凸体的最高温度基本都处于450.0 ℃左右,这是由于最大闪温点一般都是分形粗糙曲面的最高点,也是分形粗糙曲面最大接触压力点.由前文分析可知,不同接触表面最大接触压力值虽有较小波动,但是其值相差不大,因此，最高闪温点由于摩擦生热所产生的热量也相近,最高闪温点的温度也近似相同.但由于载荷增大、热区增多的原因,次闪温点的数量也会增多,且受到热区增多的影响,非接触区域受到更多热区热传导的作用,因此，载荷越大非接触区域单位时间内温升越显著.综上所述,施加载荷的大小对于微凸体的最高闪温点的温度影响并不大,但会对热区的数量以及一些次闪温点和非接触点的温度造成一定的影响.

图7 不同施加载荷下分形粗糙表面接触压力分布云图Fig.7 Fractal rough surface contact pressure distribution at different applied loads

图8 不同施加载荷下分形粗糙表面温度分布云图Fig.8 Fractal rough surface temperature distribution at different applied loads

4 结论

本文基于W-M分形函数,建立了制动接触摩擦副三维粗糙表面模型,将两个粗糙表面简化为一个分形粗糙表面与一个光滑平面的组合.结合热传递理论及风电制动过程的实际工况,建立了制动盘与闸片粗糙表面的滑动摩擦有限元模型,模拟并分析了制动过程中粗糙表面的摩擦生热及热应力变化规律,得到如下结论:

(1) 粗糙表面的分形维数对摩擦生热有较大影响,当分形维数较小时,摩擦初期形成的热区以块状热区数量较多,而点状热区的数量偏少.随着分形维数的增大,点状热区的数量增多,而块状热区的数量减少,且粗糙体接触界面的最高温度也呈现上升的趋势.

(2) 分形粗糙表面最高温度随运动时间的变化过程可分为急剧增长和缓慢增长两个阶段.相对运动速度越高,接触区域最顶端的微凸体节点在急剧增长阶段的温升越大,在缓慢增长阶段的最高温度值也越大,并且非接触面区域的温升速率也越快.

(3) 施加载荷越大,接触点数量越多,真实的接触面积越大,且实际接触点的接触压力远大于施加载荷,但接触压力不随着载荷增大而成比例增大.随着施加载荷的增加,微凸体的最高闪温点的温度变化幅度不大,但会影响热区的数量大小与次闪温点和非接触点的温度.

参考文献:

[1] 黄健萌,高诚辉,李友遐,等.工程粗糙表面接触摩擦热力学研究进展[J].中国工程机械学报,2007(4):490-496.

HUANG J M,GAO C H,LI Y X,et al.Advances of frictional contact thermodynamics for fractal rough surfaces[J].Chinese Journal of Construction Machinery,2007(4):490-496.

[2] ARCHARD J F.Elastic deformation and the laws of friction[J].Proceedings of the Royal Society A:Mathematical Physical and Engineering Sciences,1957,243(1233):190-205.

[3] MANDELBROT B B.Fractals:form,chance,and dimension[M].San Francisco:W.H.Freeman and Company,1977.

[4] BHUSHAN M B.Fractal model of elastic-plastic contact between rough surfaces[J].ASME Journal of Tribology,1991,113:1-11.

[5] 葛世荣,TONDER K.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80.

GE S R,TONDER K.The fractal behavior and fractal characterization of rough surfaces[J].Tribology,1997,17(1):73-80

[6] 魏龙,刘其和,张鹏高.基于分形理论的滑动摩擦表面接触力学模型[J].机械工程学报,2012,48(17):106-113.

WEI L,LIU Q H,ZHANG P G.Sliding friction surface contact mechanics model based on fractal theory[J].Chinese Journal of Mechanical Engineering,2012,48(17):106-113.

[7] 邓可月,刘政,邓居军,等.W-M函数模型下表面轮廓形貌的变化规律[J].机械设计与制造,2017(1):47-50.

DENG K Y,LIU Z,DENG J J,et al.Variation of surface profile topography based on W-M function model[J].Machinery Design and Manufacture,2017(1):47-50.

[8] 韩传军,张杰,梁政.粗糙表面在滑动过程中的摩擦生热研究[J].西南石油大学学报(自然科学版),2015,37(2):159-164.

HAN C J,ZHANG J,LIANG Z.Study on frictional heating of rough surface in the sliding process[J].Journal of Southwest Petroleum University (Science and Technology Edition),2015,37(2):159-164.

[9] 李成贵,董申.三维表面微观形貌的表征趋势[J].中国机械工程,2000,11(5):488-492.

LI C G,DONG S.The trends of characterizing 3D surface microtopography[J].China Mechanical Engineering,2000,11(5):488-492.

[10] 张靖周.高等传热学[M].北京:科学出版社,2009.

ZHANG J Z.Advanced heat transfer[M].Beijing:Science Press,2009.