采用改进蝙蝠算法优化的并联机器人液压驱动误差控制研究
2018-07-05,
,
(1.新乡职业技术学院 数控技术系,河南 新乡453000; 2.合肥工业大学 机械工程学院,合肥 230009)
随着科技的进步,机器人给企业生产带来了方便.传统机器人大多数采用串联驱动机构,具有驱动空间大、运动灵活等优点,但有驱动承载力小、关节误差累积大等缺点.为了提高机器人驱动承载力和定位精度,并联机器人驱动机构应运而生.从机构学运动角度分析,并联机器人具有许多优点[1-2]:① 承载力大;② 刚度强;③ 定位精度高.因此,并联机器人在航天、海洋及医学等领域得到了广泛应用.但是,并联机器人的结构决定了其运动轨迹的复杂性,研究并联机器人运动平台的定位精度具有重要的价值.
并联机器人驱动机构在发展过程中,诞生了许多理论和方法.例如:文献[3-4]研究了并联机器人结构设计,分析了并联机器人正运动学和工作空间,推导了并联机器人的正运动学方程式,求解几何参数,从而设计出并联机器人液压驱动机构;文献[5-6]研究了并联机器人的轨迹跟踪控制,建立了并联机构逆运动学模型,引用了模糊PID控制器控制机器人运动轨迹,通过仿真验证轨迹跟踪效果,提高了控制系统的稳定性;文献[7]研究了并联机器人运动轨迹的生成方法,利用图像格式提取运动轨迹特征点,采用Matlab软件进行特征点曲线拟合,通过实验验证了可行性,快速地生成机器人运动轨迹.以往研究并联机器人运动平台轨迹定位精度较低,不能满足高精度轨迹跟踪的要求.对此,本文采用差分进化算法融合蝙蝠算法优化级联控制参数,将优化后的级联控制用于驱动并联机器人运动平台的轨迹跟踪,通过Matlab软件对运动平台定位精度进行仿真验证,并且与蝙蝠算法优化结果进行对比和分析,为进一步研究并联机器人运动平台轨迹跟踪提供了理论基础.
1 并联机器人分析
并联机器人如图1所示,主要包括运动平台、固定平台和6个可扩展的驱动器.驱动器由6个相应的液压阀控活塞伺服驱动系统,控制良好的驱动器长度和它们之间的完美配合,使上运动平台遵循所期望的运动轨迹.上平台的驱动,采用液压伺服控制系统,由6个气缸伺服阀组成,如图2所示.
液压缸阀控制的数学模型[8]可以表示为
(1)

图1 并联机器人驱动机构Fig.1 Parallel robot driving mechanism
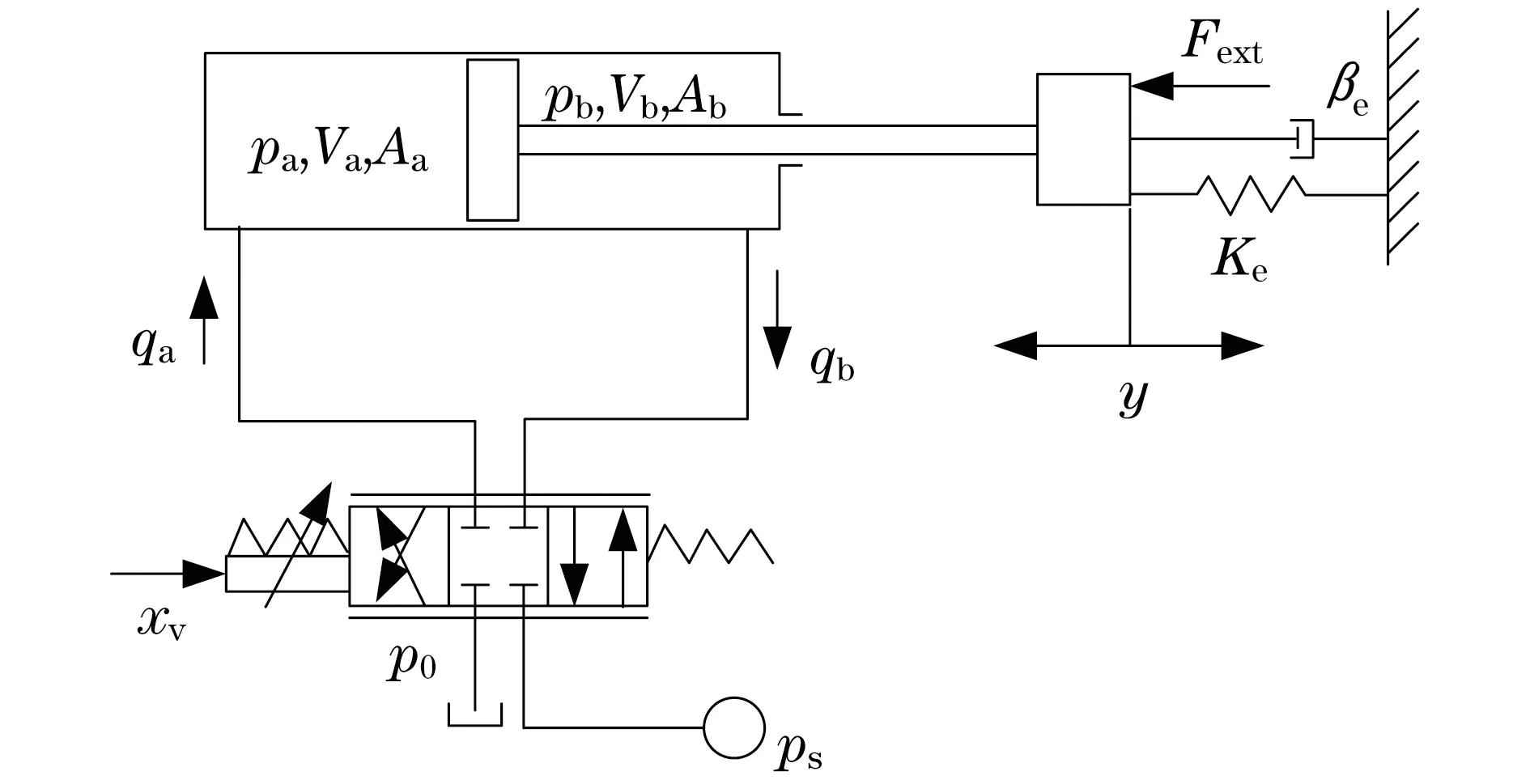
图2 阀控非对称活塞示意图Fig.2 Valve controlled asymmetric piston diagram
式中:y为活塞位移;mt为活塞总质量;Aa为活塞头一侧的有效面积;Ab为活塞杆一侧的有效面积;α=Ab/Aa;pa,pb分别为前进和返回压力;Ff为摩擦力;Ke为负载弹簧刚度;Fext为活塞上干扰力;βe为液体体积弹性模量;Va0和Vb0为初始单杠容积;cvi> 0为阀孔的流量系数;xv为阀移动位移;ps为供应压力;p0为油箱压力;cLi为内部泄漏系数;L为活塞冲程.如果x≥0,则函数sg(x)等于x;如果x<0,则sg(x)等于0.
2 级联控制器的优化设计
级联控制FL由两个循环组成:内环控制和外环控制.内环控制是实际的制动器控制回路,它的目标是通过输入输出线性化来控制执行机构的压力差;外环控制涉及到执行器负载的稳定控制和外部外力Fext的补偿.
如图3所示,非线性控制设计的输入输出线性化方法:从子系统压力动态FL和控制输入u之间找出输出的直接关系,其控制方程式[9]为
(4)
在u和FL之间,对应的输出导数设置为新的输入v,采用这种非线性关系,系统可以输出期望的运动轨迹.v的控制方程式为
(5)
式中:P,I,D分别为比例系数、积分系数及微分系数;e(t)=FL,ref-FL.
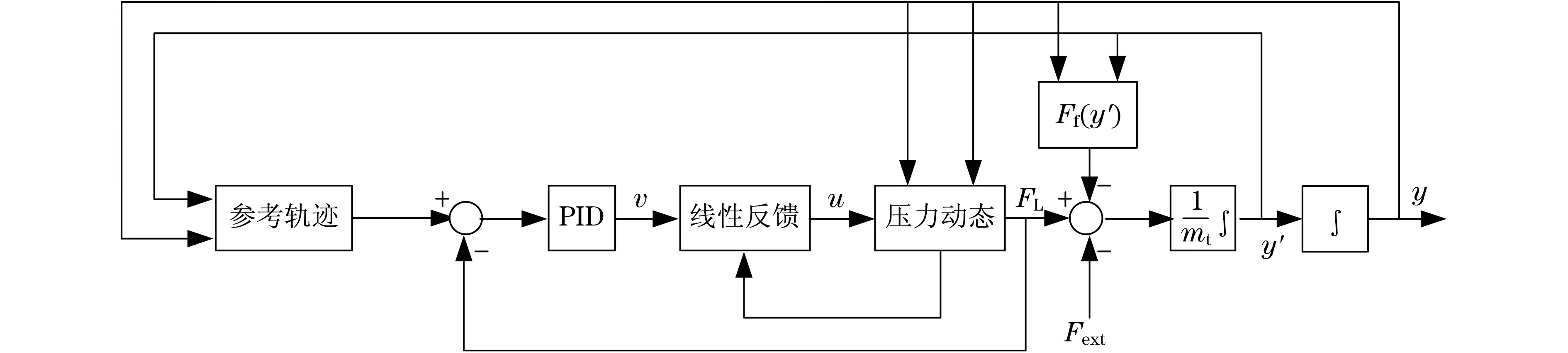
图3 液压执行机构级联控制的结构框图Fig.3 Structure block diagram of cascade control of hydraulic actuator
约束最优问题可以通过目标函数f(x)表达,f(x)的最优化与设计参数x有关,可以写为
式中:εi(t)(i= 1,2,…,6)为第i根驱动活塞位置误差,ε(t)=[ε1(t),ε2(t),…,ε6(t)]T为位置误差向量,t为时间间隔.
每个控制器有3个设计参数变量:
(8)
式中:x=[x1,x2,…,x18]T为设计参数向量.
目标函数是在满足约束条件的同时,找到优化目标函数的变量值.指定约束gi的可行空间如下:
F={x∈R18|gi(x)<0,i=1,2,…,18}
(9)
假设虚拟目标函数为fv(x),Rn→R满足下列条件:① 若x∈F,则fv(x)<0;② 若f(xa) (10) 根据定义的虚拟目标函数fv(x),原约束优化问题(6)修正后为 (11) 式中:gmax(x)=max[g1(x),g2(x),…,g18(x)],gi(x)为式(7)中的第i个约束. 蝙蝠算法利用超声波对障碍物进行探测和定位,从而搜索到全局最优解的一种启发式智能算法.具体操作步骤如下: 步骤1种群初始化.在D维空间随机产生初始值,主要包括:① 种群数量NP;② 最大脉冲频率R0;③ 最大脉冲音量A0;④ 频率取值范围[fmin,fmax];⑤ 音量衰减系数α;⑥ 频率增强系数γ;⑦ 搜索精度ε. 步骤2根据蝙蝠初始位置xi,搜索当前最优解x*. 步骤3更新蝙蝠的速度、位置及脉冲频率,其变化迭代公式[10]为 (12) 步骤4随机生成均匀分布数r0,若r0>ri,则对当前最优值进行扰动,生成新的解,并对新解进行处理;若r0 (13) 步骤5对所有当前最优值进行重新排序,直到搜索到全局最优值或达到最大迭代次数为止. 差分进化算法类似于遗传算法,也有变异、交叉与选择操作,具体操作步骤如下: 步骤1种群初始化.在D维空间内随机生成NP个个体位置xi(t). 步骤2变异操作.从初始种群中随机选择3个互不相同的个体,进行变异操作方程式[11]为 vij(k)=xa(k)+F[xb(k)-xc(k)] (14) 式中:a,b,c为随机数,取值范围为[1,2,…,NP],NP为种群大小;F为缩放因子,取值范围为[0,2]. 步骤3交叉操作.将变异后个体与变异前个体进行交叉操作,从而得到新的个体,其交叉方程式[11]为 (15) 式中:λ为交叉概率,取值范围为[0,1];r0为均匀分布随机数,取值范围为[0,1];rn为随机整数,取值范围为[1,N]. 步骤4选择操作.根据适应度函数比较uij(k+1)和xi(k),从而生成下一代个体xi(k+1): xi(k+1)= (16) 步骤5输出最优值.反复操作步骤1~步骤4,直到输出群体最优位置. 蝙蝠算法和差分进化算法在优化复杂问题时,容易陷入局部最优值.因此,本文采用差分进化算法融合蝙蝠群算法,具体操作步骤如下: 步骤1初始化种群的各个参数; 步骤2判断种群个体适应度值,得出当前最优解; 步骤3根据式(15)和式(16)更新蝙蝠搜索速度、位置及脉冲频率; 步骤4扰动当前最优解,生成一个新解,并处理新解; 步骤5根据r0 步骤6采用差分进化算法对初始参数进行变异、交叉及选择操作,输出新的蝙蝠位置; 步骤7由蝙蝠个体适应度值来更新当前最优位置,不断迭代最优值,直到满足最优值为止,否则,转到步骤3. 改进蝙蝠算法与蝙蝠算法的差别在于:改进蝙蝠算法在迭代后生成新的值,不是直接用于下一次迭代,而是经过个体之间的变异、交叉和选择操作,得到当前最优值后,再进入下一次迭代.因此,改进蝙蝠算法全局搜索能力较强,避免搜索过程中产生局部最优解. 采用改进蝙蝠算法对机器人运动平台控制进行优化,初始条件参数设置:种群大小为100,最大迭代次数为400,最大脉冲频率R0=0.5,最大脉冲音量A0=0.25,交叉概率为0.05,变异缩放因子为0.65,优化后的级联控制参数如表1所示 表1 级联控制器参数优化值Tab.1 Parameter optimization of cascade controller 为了对比蝙蝠算法和改进蝙蝠算法的搜索效果,采用级联控制机器人运动平台轨迹跟踪误差进行验证,运动平台期望运动轨迹为x=0.2·sin(2πt),y=0.3sin(2πt+π/2),z=1.4+0.4·sin(2πt),仿真参数如表2所示.在Matlab软件中进行轨迹跟踪误差仿真,采用蝙蝠算法优化级联控制的机器人运动平台轨迹跟踪误差如图4所示.采用改进蝙蝠算法优化级联控制的机器人运动平台轨迹跟踪误差如图5所示. 表2 并联机器人仿真参数Tab.2 Simulation parameters of parallel robot 图4 蝙蝠算法优化级联控制仿真结果Fig.4 Optimization of cascade control simulation results of bat algorithm 图5 改进蝙蝠算法优化级联控制仿真结果Fig.5 Optimizing the bat algorithm to optimize the simulation results of cascade control 对比图4和图5仿真结果可知,并联机器人运动平台在执行轨迹跟踪任务时,采用蝙蝠算法优化级联控制所产生的最大误差如下:x轴最大误差为1.3×10-2m,y轴最大误差为1.8×10-2m,z轴最大误差为2.6×10-2m;而采用改进蝙蝠算法优化级联控制所产生的最大误差如下:x轴最大误差为1.5×10-4m,y轴最大误差为1.9×10-4m,z轴最大误差为2.5× 10-4m.改进后,并联机器人运动平台轨迹跟踪产生的误差小.因此,采用改进蝙蝠算法优化级联控制,在相同的控制条件下,可以提高并联机器人运动平台控制精度. 本文研究了并联机器人运动平台定位精度,创建了并联机器人液压驱动结构简图,设计了液压驱动运动平台的级联控制方程式.构造定位误差目标函数,给出设计变量和约束条件.引用差分进化算法和蝙蝠算法对级联控制目标函数进行优化.在Matlab环境下,对运动平台三维方向进行跟踪误差仿真,并与蝙蝠算法优化级联控制效果形成对比.仿真数据表明,改进蝙蝠算法优化后的级联控制,运动平台在x,y,z轴方向轨迹跟踪产生的误差较小,提高了液压驱动机构的定位精度. 参考文献: [1] 李冰冰.基于粒子群算法的并联机器人位姿误差建模与补偿方法研究[D].沈阳:东北大学,2014. LI B B.Research on pose error modeling compensation of parallel robot based and on PSO[D].Shengyang:Northeastern University,2014. [2] 丁琴琴.基于RBF神经网络调节切换增益的并联机器人滑模控制研究[D].镇江:江苏大学,2012. DING Q Q.Sliding mode control of parallel manipulators based on RBF neural network for switching gain control[D].Zhenjiang:Jiangsu University,2012. [3] 刘兰波,唐志勇,裴忠才.6自由度液压并联机器人结构优化设计[J].机床与液压,2014,42(23):119-121. LIU L B,TANG Z Y,PEI Z C.Structural optimization design of a 6-DOF hydraulic parallel robot[J].Machine Tool and Hydraulics,2014,42(23):119-121. [4] FILIPOVIC M,DJURIC A,KEVAC L.The rigid S-type cable suspended parallel robot design,modelling and analysis[J].Robotica,2016,34(9):1950-1958. [5] 李一龙,严智敏.基于模糊PID对3-RPS并联机器人轨迹跟踪控制[J].测试技术学报,2016,30(1):24-28. LI Y L,YAN Z M.Trajectory tracking control of 3-RPS parallel robot based on fuzzy PID[J].Journal of Test and Measurement Technology,2016,30(1):24-28. [6] POUR R K,KHAJVAND H,MOOSAVIAN S A A.Fuzzy logic trajectory tracking control of a 3-RRS ball and plate parallel manipulator[J].International Conference on Robotics and Mechatronics,2016(28):343-348. [7] 马国庆,刘丽,于正林,等.6自由度并联机器人轨迹生成及实验研究[J].长春理工大学学报(自然科学版),2015,38(5):54-57. MA G Q,LIU L,YU Z L,et al.Trajectory generation and experiment research of 6-DOF parallel robot[J].Journal of Changchun University of Science and Technology (Natural Science Edition),2015,38(5):54-57. [8] GUO H B,LIU Y G,LIU G R,et al.Cascade control of a hydraulically driven 6-DOF parallel robot manipulator based on a sliding mode[J].Control Engineering Practice,2008,16(9):1056-1067. [9] NEDIC N,STOJANOVIC V,DJORDJEVIC V.Optimal control of hydraulically driven parallel robot platform based on firefly algorithm[J].Nonlinear Dynamics,2015,82(3):1458-1472. [10] 何子旷.蝙蝠算法的改进与应用[D].广州:广东工业大学,2013. HE Z K.Improvement and application of the bat algorithm[D].Guangzhou:Guangdong University of Technology,2013. [11] 周钦亚.动态环境中差分进化算法的研究[D].郑州:郑州大学,2014. ZHOU Q Y.The research of differential evolution under dynamic environment[D].Zhengzhou:Zhengzhou University,2014.3 改进蝙蝠算法
3.1 蝙蝠算法
3.2 差分进化算法
3.3 改进蝙蝠算法
4 仿真及分析

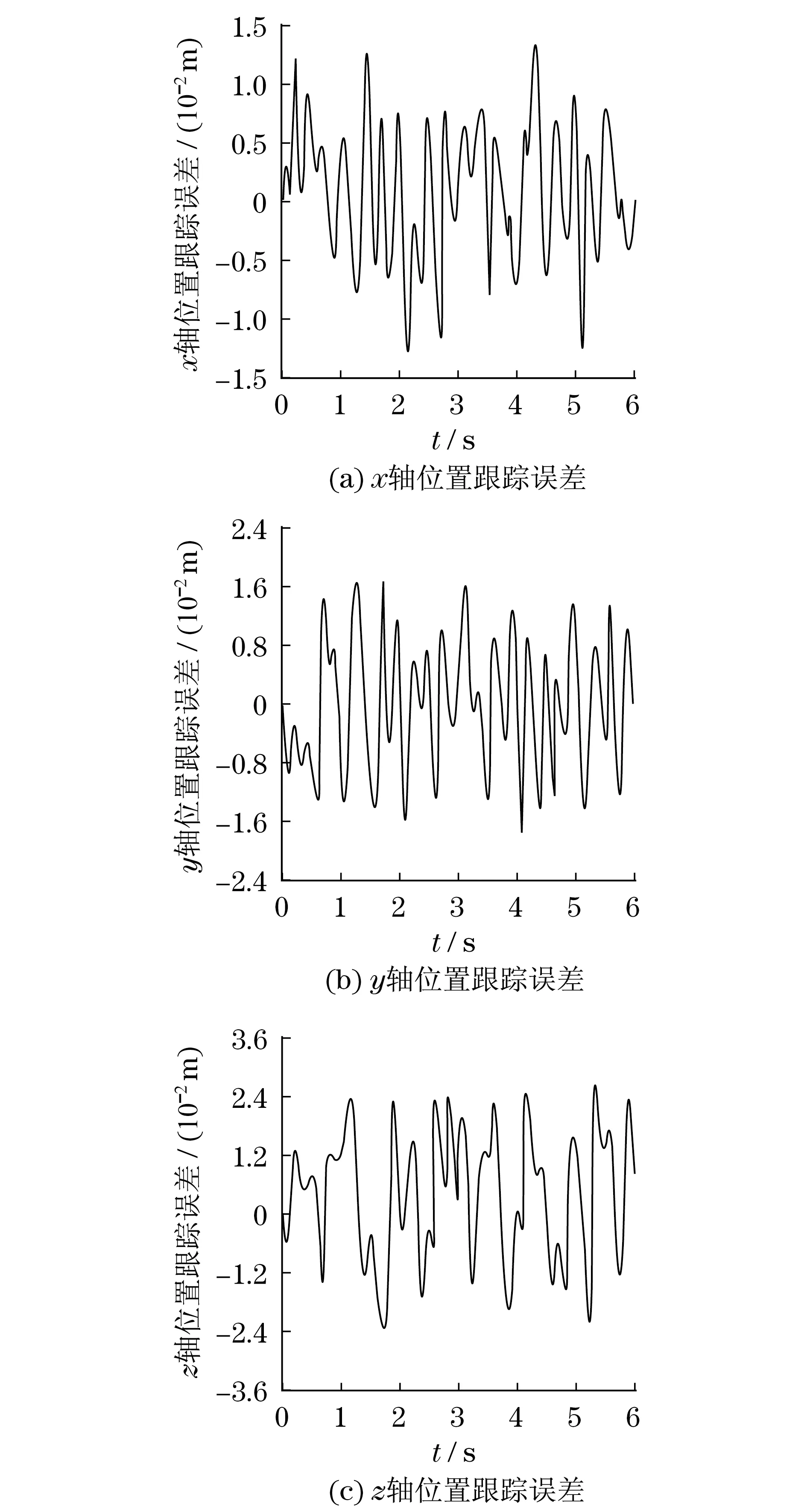
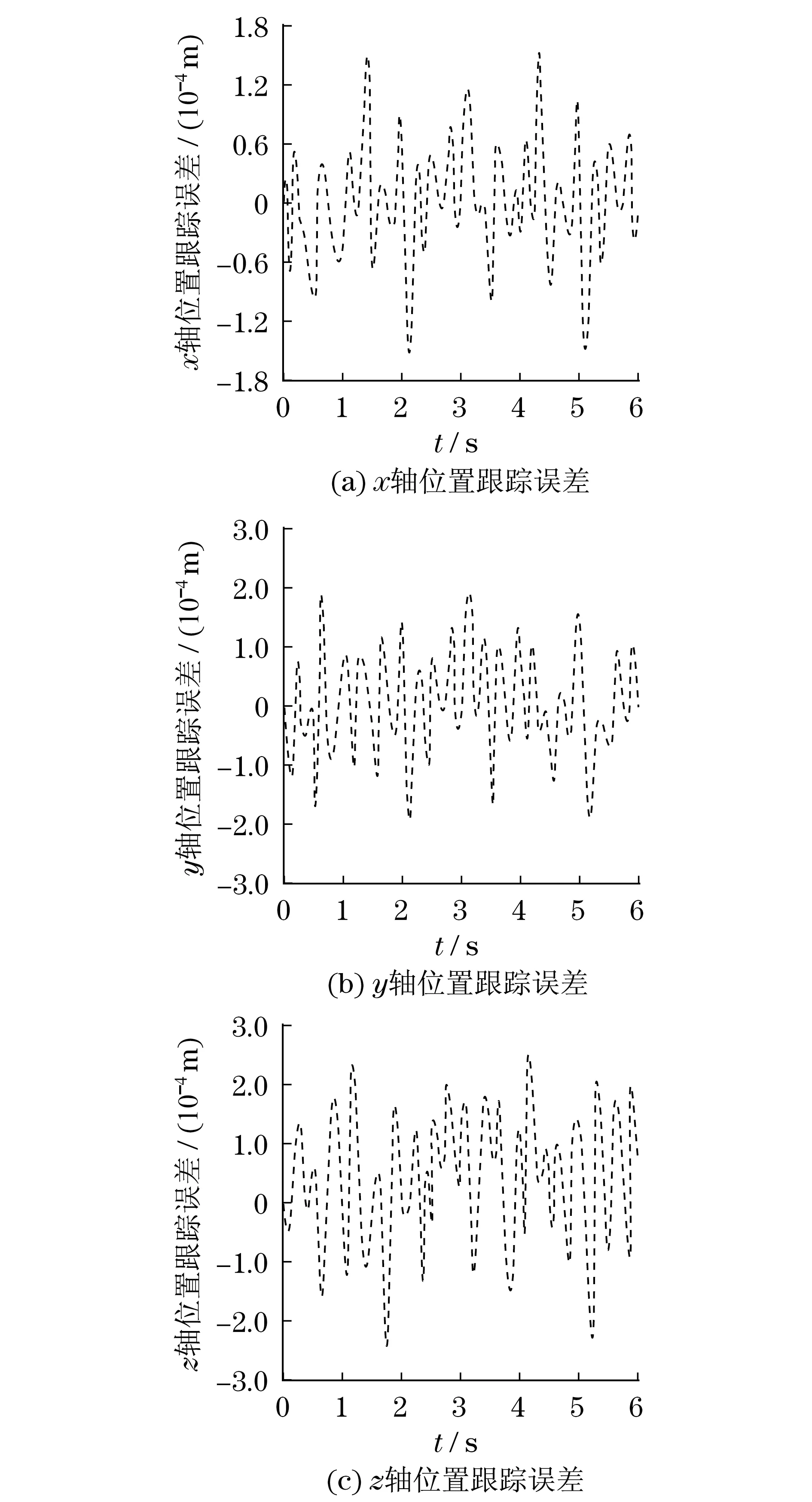
5 结语
