基于改进三次B样条曲线的奶牛点云缺失区域修复方法

何东健 牛金玉 张子儒 郭阳阳 谭 益

(1.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100； 2.农业部农业物联网重点实验室， 陕西杨凌 712100； 3.陕西省农业信息感知与智能服务重点实验室， 陕西杨凌 712100)

0 引言

奶牛养殖业在我国国民经济中具有重要的战略地位[1-2]。奶牛的规模化标准养殖是提升我国奶业竞争力和品质的必经之路，也是我国奶牛产业发展的必然要求[3]。规模化标准养殖需要优良的奶牛品种，而奶牛的体型评定对选育适应机械化挤奶的优良奶牛品种具有重要意义。

奶牛的三维点云数据包含奶牛身体尺寸和外形等几何信息，因此，获取奶牛的三维点云数据对奶牛的体型评价、体尺测量以及健康状况评定和行为模型研究均具有重要的应用价值[4]。目前，获取三维点云数据的途径主要有双目立体视觉系统、深度相机和激光扫描仪等[5]，由于环境和设备精度影响，特别是奶牛养殖场围栏等复杂环境因素，导致获取的点云存在孔洞现象，点云孔洞不仅使模型实现正确的可视化受限，而且严重影响点云的后期处理工作[6-7]。

国内外学者针对点云孔洞修复问题进行了许多研究。WANG等[8]使用移动最小二乘法并依据模型的几何形状和阴影信息对孔洞进行拟合重建；CHALMOVIANSKY等[9]首先计算模型中每个点的邻近点，以此确定孔洞边界，然后使用边界的邻近点构造代数曲面片填充孔洞；MARCHANDISE等[10]通过正交梯度法求解径向基函数在任意曲面上的偏微分方程，较好地修补了网格模型中存在的孔洞。NGO等[11]将复杂的孔洞分成较小的简单子孔洞，再用三角网格算法修补子孔洞，最终完成复杂孔洞修补。QUINSAT等[12]以数值模型的先验知识作为名义网格，识别出数字化孔洞后，计算名义网格和点云之间的差异，然后确定最小化的变形能量进行网格变形，对点云模型上的孔洞进行修补。蒋刚[13]先对空间采样点曲线在3个坐标平面上投影，然后用支持向量机分别对3组二维投影数据进行回归运算，计算得到孔洞的三维坐标，完成孔洞修补；陈相等[6]利用三角形网格特征寻找到孔洞边界，然后依据孔洞边界夹角进行三角形网格填充，得到修补效果较好的点云模型。晏海平等[14]提出一种基于径向基函数的孔洞修复算法，该算法提取孔洞多边形边界特征并用最小二乘法填充孔洞，再建立孔洞边界点和邻域信息的径向基隐式曲面，结合梯度下降法调整孔洞填充点的位置，实现点云孔洞的修复。上述算法均针对区域相对较小的封闭孔洞进行修复，而去除遮挡栏杆后的奶牛点云，不仅点云缺失区域大，且为非封闭孔洞，上述算法难以有效对非封闭较大孔洞进行修复。

为解决奶牛点云非封闭较大孔洞的修复问题，本文提出一种基于改进三次B样条曲线的修复方法，以提高奶牛点云模型精度。

1 奶牛点云数据获取及预处理

1.1 奶牛点云数据获取

在陕西省杨凌科元克隆股份有限公司奶牛养殖场，用美国微软公司Kinect v2体感设备(简称Kinect)及配套软件，采集健康荷斯坦奶牛深度数据。

安装在支架上的Kinect设置于活动场和挤奶间栏杆通道(长约4 m，宽约1.4 m)一侧，Kinect传感器有效检测范围为0.5～4.5 m，为有效拍摄到奶牛多帧全身点云且降低环境点云影响，故视野范围应覆盖此段栏杆通道，经测试，将Kinect放置于其中心距最近栏杆(直径0.05 m)轴线2.15 m处，距离地面高度为0.9 m。当奶牛整个身体完全进入Kinect的视野范围时，开始采集深度码流数据，采集帧率30 f/s，深度图像分辨率为512像素(水平)×424像素(垂直)，数据保存在便携式计算机固态硬盘(三星850 EVO SATA3，120 G)中。

于2017年3月24—30日20:00—21:30，采集45头奶牛全身侧视深度数据，每头奶牛采集5帧，共计225帧。

1.2 点云数据预处理

在台式计算机(CPU为Intel Core i5-4590 3.3 GHz、8 GB内存)上，用Microsoft Visual Studio 2013、PCL点云库、Matlab R2017a进行数据处理。

由于拍摄环境复杂，获取的点云中除奶牛外，还包括地面、水平栏杆、竖直栏杆等干扰，故需要去除非奶牛点云数据，如图1所示，点云数据坐标系以红外摄像头感光元件中心为坐标原点o，x轴水平向左，y轴竖直向上，z轴沿拍摄方向垂直xoy面。

图1 Kinect获取的奶牛点云Fig.1 Dairy cow’s point cloud obtained by Kinect

奶牛点云预处理流程如图2所示，具体步骤为：①用直通滤波方法去除部分背景点云，如图3a所示。②用查询点与邻域点集之间平均距离估计方法[15]过滤环境中的离群点。③用带法线的平面模板匹配法去除地面点云数据，如图3b所示。④用与给定轴线平行的直线模板匹配法去除水平栏杆点云。⑤用查询点与邻域点集之间平均距离估计的方法去除余留下的少量栏杆边缘噪声点，如图3c所示。⑥对于竖直栏杆和与之相连的少量地面点云数据，用欧氏聚类方法[16]予以去除，最终得到奶牛个体的点云数据，如图3d所示。

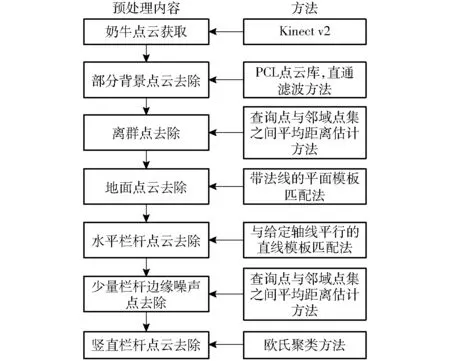
图2 预处理流程图Fig.2 Flow chart of preprocessing

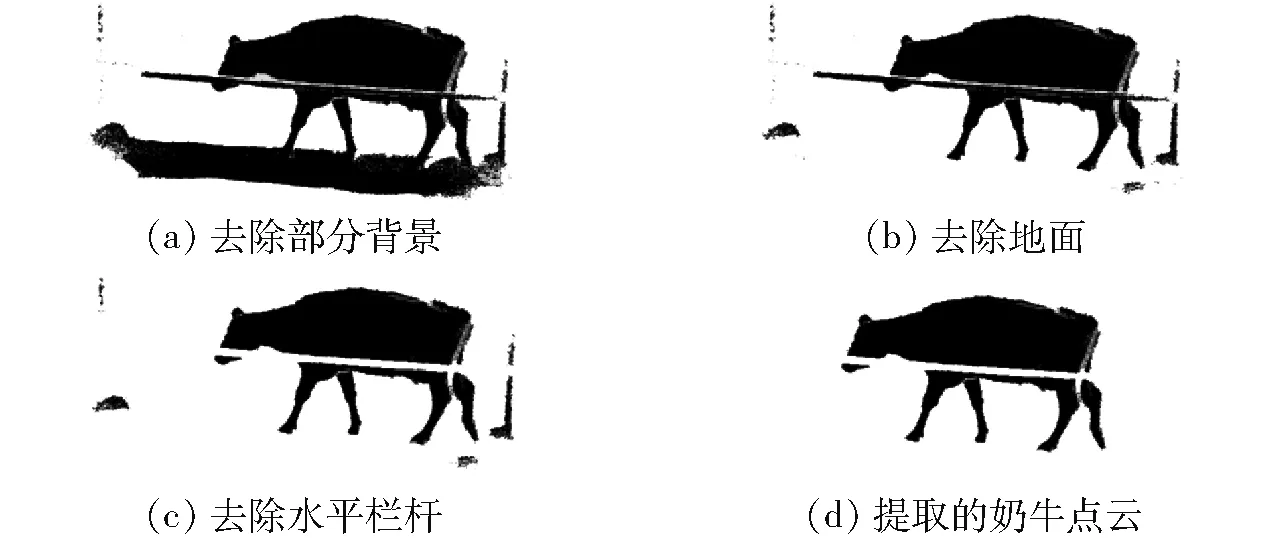
图3 奶牛点云预处理结果Fig.3 Results of preprocessing dairy cow’s point cloud

2 奶牛缺失区域修复方法

经过预处理后的奶牛点云存在被水平栏杆遮挡的缺失较大的区域，将对后续体尺参数提取产生重要影响，故本文提出了基于改进的三次B样条曲线的点云修复方法。先去除环境背景后的奶牛点云进行切片投影，再对每个切片点列中间距较大的相邻点进行补点，最后对补点后得到的新点列进行三次B样条曲线拟合，即得到修复后奶牛点云。

2.1 奶牛点云切片投影

奶牛点云缺失区域基本沿x轴方向且上下侧均有点云，故可用上下侧点云信息修复缺失区域。先将点云沿x轴进行切片投影处理，步骤如下：

(1)确定奶牛点云中点与点之间最小空间距离dmin，沿x轴方向以dmin等间隔将点云切片采样为N份。由于部分切片采样点云中存在断连间隔，故对切片宽度前后分别扩展dmin。

(2)考虑到扩展切片采样区间后点数增加较多，对曲线拟合有较大影响，故对每个切片点云沿y轴以dmin等间隔将切片点云分为Ni份，对每份取其所有点的中心作为该份的代表点。

(3)将沿x轴方向切片的点云向yoz面投影，再对投影的点进行三次B样条曲线拟合，将获得的新点列还原到三维空间时，将x坐标设置为切片采样区间中点。对N份点云切片做同样处理。

奶牛前后肢处切片投影相对复杂且具有代表性，故选取前肢处一切片投影作为拟合的典型代表，其点云切片投影如图4所示。

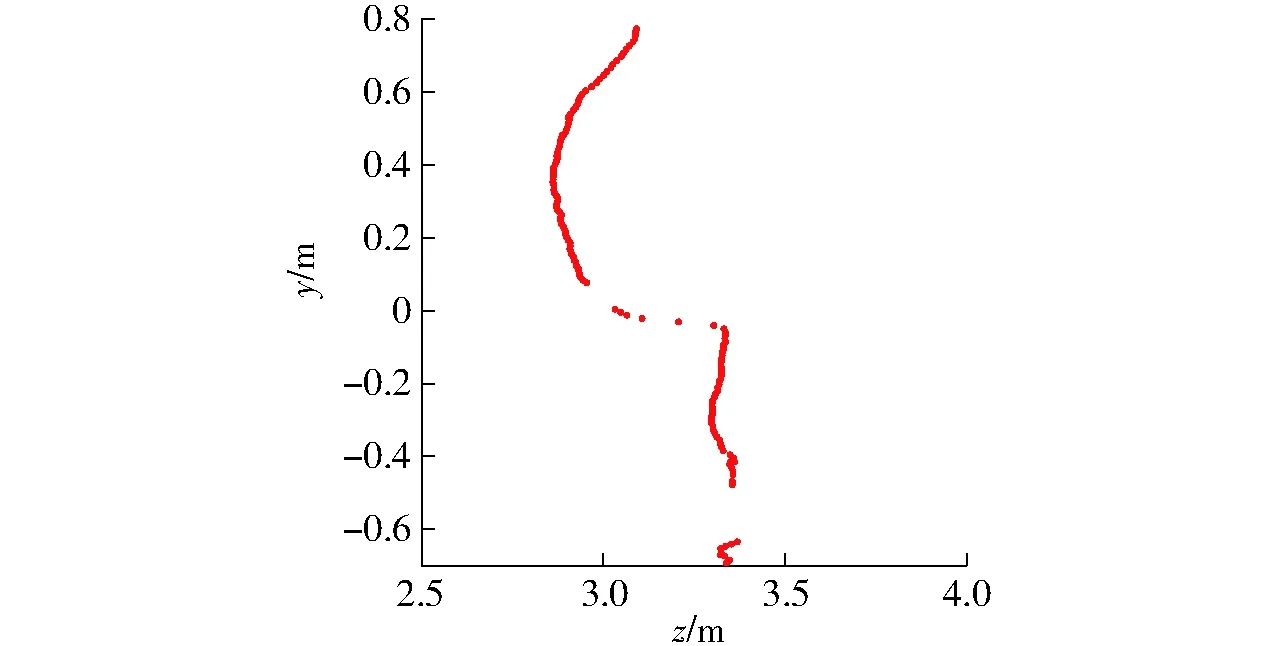
图4 奶牛前肢点云切片投影Fig.4 Slice projection of dairy cow’s forelimb point cloud

2.2 奶牛点云切片投影的拟合方法

不同部位的奶牛点云切片投影形状和点数各不相同，且相邻点之间密集程度差异较大，故无法用最小二乘法[17-19]确定通用拟合函数以拟合不同切片投影，使用样条曲线[20-21]易出现过拟合现象，而三次B样条曲线[22-25]具有局部性、凸包性等性质，可由4个点拟合一段曲线，且不会出现过拟合现象，故本文用三次B样条曲线对奶牛点云切片投影进行拟合。

2.2.1三次B样条曲线拟合

对于任意相邻的4个顶点Pi、Pi+1、Pi+2、Pi+3，三次B样条曲线段表达式为

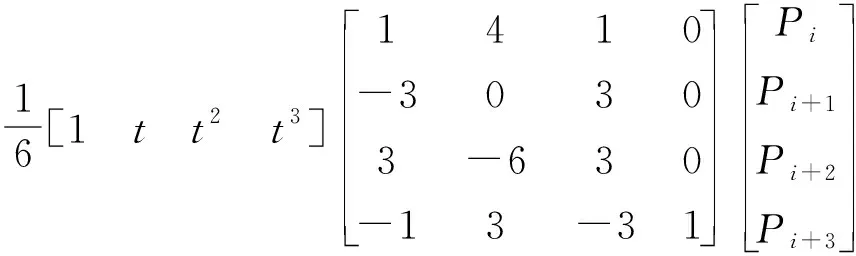
(1)

对三次B样条方法拟合后的曲线进行拟合取点时，取决于参数t的取值，为了使拟合点列均匀，可将t均匀取值。但因奶牛点云中存在水平栏杆遮挡，切片投影中存在间隔较大的相邻点，因此，用三次B样条曲线对切片投影进行拟合时，若参数t均匀取值，则拟合后在间隔较大的相邻点处会出现点列稀疏问题。如图5所示，对奶牛肢蹄处切片投影点云分别进行三次B样条曲线拟合，由局部放大图可以看出，在原点列间隔较大处拟合得到的新点列均匀性较差。

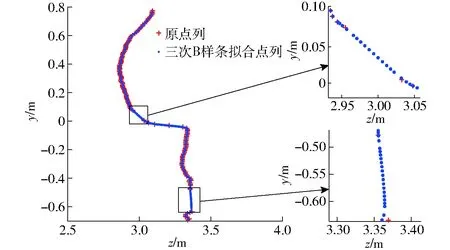
图5 三次B样条曲线拟合Fig.5 Cubic B-spline curve fitting

2.2.2改进的三次B样条拟合方法

针对三次B样条曲线拟合出现的点列稀疏问题，一种方法是再次用三次B样条曲线拟合，但这会使拟合的曲线更加偏离原曲线位置，而且拟合的形状与原曲线差异更大；另一种方法是先对其进行补点，再用三次B样条曲线拟合，该方法可以使拟合的曲线更加逼近原曲线，如文献[25]中增加型值点的方法。但本文中奶牛切片投影存在较大的间隔区域，文献[25]的补点方法会使增加的点超出补点区域，导致拟合曲线局部偏差较大。为此，本文对文献[25]方法进行改进，提出一种对较大间隔区域补点的方法，然后再用三次B样条曲线拟合，以使拟合的曲线更加逼近原曲线。

改进方法原理如图6所示，具体步骤如下：

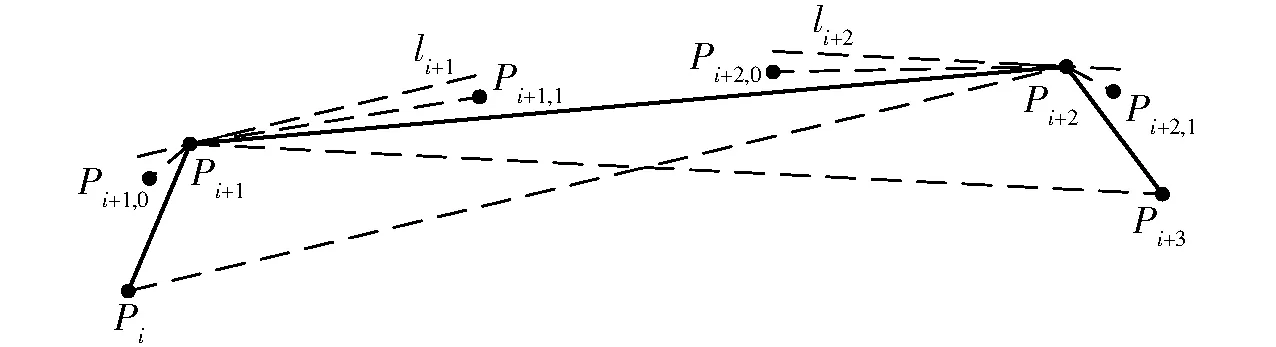
图6 补点示意图Fig.6 Diagram of adding points

(1)已知Pi、Pi+1、Pi+2、Pi+3为平面上的点列，过Pi+1点作PiPi+2的平行线li+1，过Pi+2点作Pi+1Pi+3的平行线li+2。

(2)设补点间距阈值为L，若|Pi+1Pi|≥L、|Pi+1Pi+2|≥L，则分别做li+1与Pi+1Pi和Pi+1Pi+2夹角的角平分线Pi+1Pi+1,0和Pi+1Pi+1,1，使

(2)

式中h——比例系数

若相邻点间距小于L，则不进行补点。

同理，在Pi+2点处可得到Pi+2,0和Pi+2,1点。

(3)将Pi、Pi+1,0、Pi+1、Pi+1,1、Pi+2,0、Pi+2、Pi+2,1、Pi+3按顺序合并成新点列，再返回步骤(1)、(2)，直到所有相邻点间距均小于L。

(4)将补点后得到的新点列进行B样条曲线拟合，即可得到平滑的点列。

3 试验结果与分析

为了验证本文方法对奶牛点云栏杆遮挡较大缺失区域的修复性能，验证以下方面：

(1)奶牛典型肢体部位切片投影拟合后点列的均匀性以及拟合点列对原点列的逼近性能。点列的均匀性用相邻点间距均值和标准差评价；拟合点列对原点列的逼近性能用切片逼近误差评价，即计算原点列的每个点与拟合点列中点的最小间距，将所有最小间距的均值作为切片逼近误差。

(2)拟合后的每帧奶牛点云对原点云的逼近性能。用帧逼近误差，即每帧奶牛点云所有切片逼近误差的均值，评价对原点云的逼近性能。

3.1 参数h和L取值分析

本文算法中直接影响点云切片投影均匀性和逼近性能的参数是比例系数h和间距阈值L，因此需对二者的较优取值进行试验。

对图4所示的前肢处切片投影，分别取h为1/6、1/5、1/4和1/3，L/dmin在1～20间取整数进行拟合，统计相邻点间距均值、标准差以及拟合后点数和切片逼近误差，如图7所示。

分析图7可知，当L/dmin=1时，相邻点间距均值、标准差和逼近误差达到最小，但均值小于拟合间距dmin(该帧点云为7.114 mm)的0.5倍，同时，拟合后点数也大于三次B样条方法获得点数的2倍，点数的成倍增加会对后期奶牛点云体尺提取效率等产生重要影响。当h取值为1/4，L/dmin取值为5时，可使标准差和逼近误差达到较小值。

取h=1/4，L/dmin=5，对奶牛前肢处点云切片投影进行拟合，结果如图8所示，拟合后相邻点间距均值为7.552 mm，标准差为1.305 mm，逼近误差为0.720 mm，点数由拟合前150个增加到拟合后的256个，与图5仅用三次B样条曲线拟合相比，本文方法拟合后点列较为均匀，且更逼近原点列。

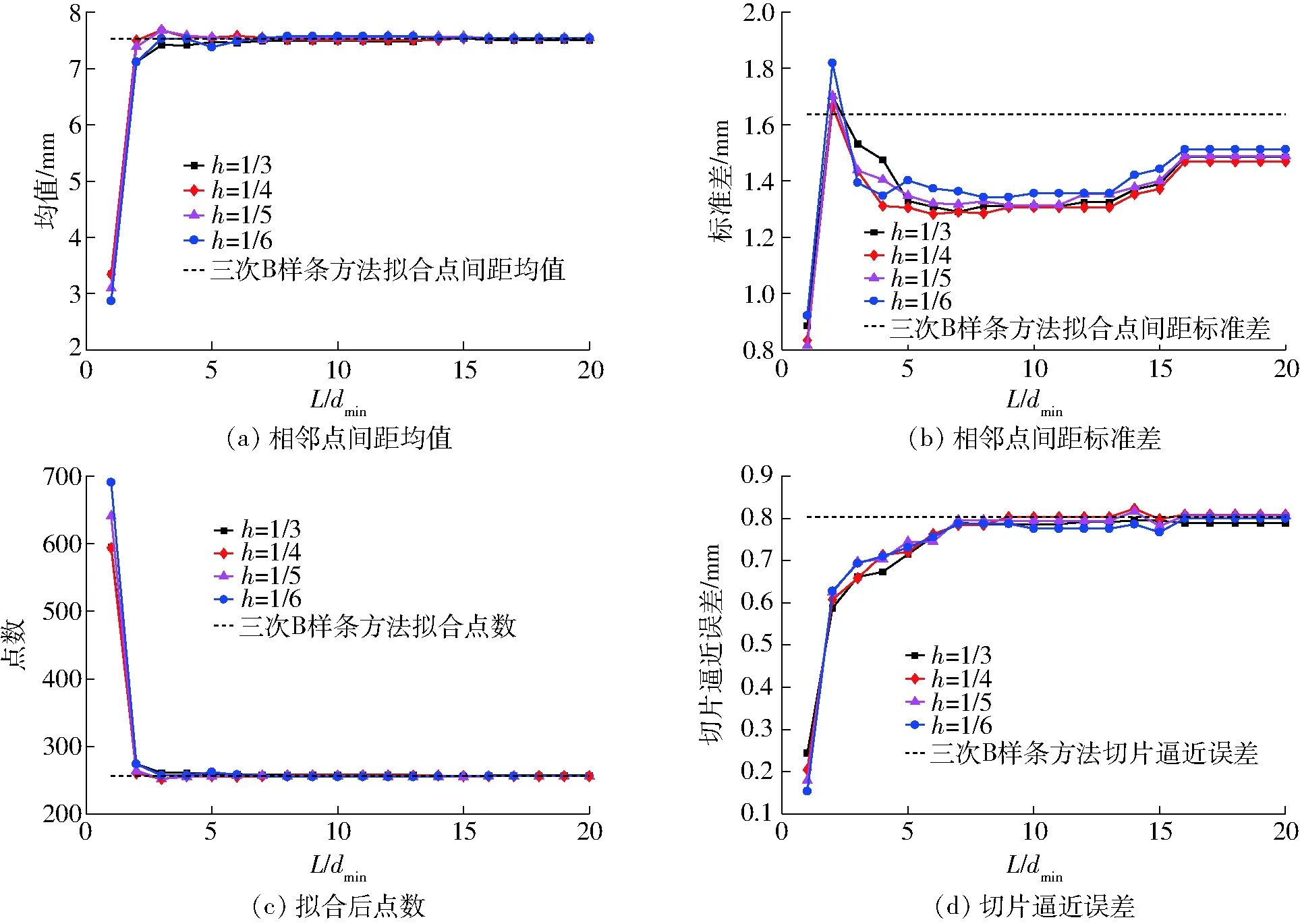
图7 奶牛前肢处点云切片投影拟合结果Fig.7 Fitting results of slice projection constructed by point cloud of dairy cow’s forelimb

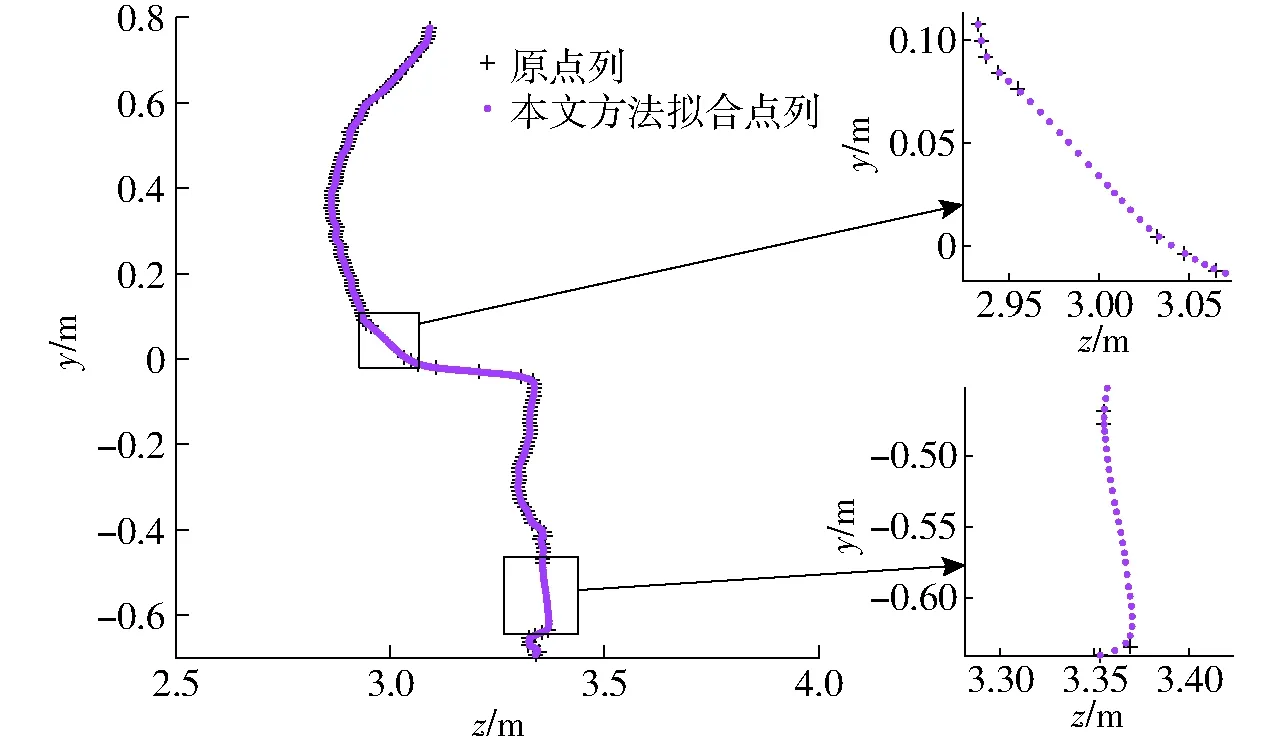
图8 本文方法拟合结果Fig.8 Fitting result of proposed method

3.2 奶牛拟合点云逼近性能分析

取h=1/4，L=5dmin，用本文方法对45头奶牛的225帧点云进行栏杆遮挡缺失区域修补，计算出帧逼近误差和平均帧逼近误差，如图9所示。从图9可知，仅用三次B样条曲线拟合得到的平均帧逼近误差为2.214 mm，最大和最小帧逼近误差为3.918 mm和0.819 mm，而本文方法得到的平均帧逼近误差为1.623 mm，最大和最小帧逼近误差为2.547 mm和0.737 0 mm，平均帧逼近误差降低了26.7%，更加逼近原点云。

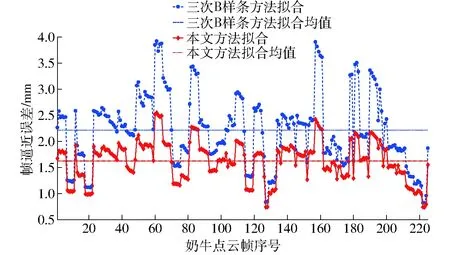
图9 奶牛点云帧逼近误差Fig.9 Fitting error of dairy cow’s point cloud by frame

图10为三次B样条方法和本文方法修复效果图，图10a～10d为未修复的整体和局部细节图，图10e～10h为三次B样条曲线修复得到的整体和局部细节图，图10i～10l为使用本文算法修复得到的整体和局部细节图。可以看出，图10f与10g在奶牛点云栏杆遮挡区域边缘有明显的空缺，而本文方法得到的图10j与10k在栏杆遮挡区域边缘的修复效果较好。从奶牛点云的背部俯视图可以看出，三次B样条方法和本文方法对较小间隔均能取得较好的修复效果，但在背部有较大间隔处，本文方法修复效果更好。

图10 奶牛点云修复效果对比图Fig.10 Repairing effect comparison of dairy cow’s point cloud

从图10中还可以看出，在奶牛头部点云缺失区域，仍存在未得到修复的区域，这是因为该处点云缺失区域仅一侧有点云信息，而另一侧无点云信息。

3.3 噪声敏感性试验

由于奶牛身体存在黑白块区域，Kinect发出的红外光会被黑色区域吸收一部分，导致获取的点云存在噪声。为考察噪声对本文方法拟合效果的影响，对含有噪声的奶牛点云用本文方法进行拟合试验，结果如图11所示。

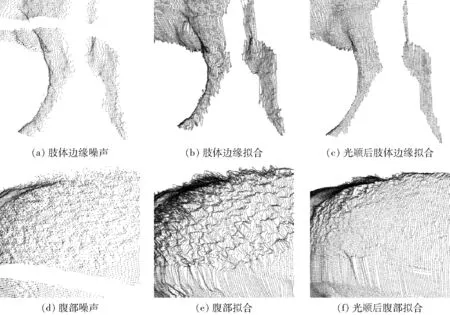
图11 噪声对本文方法的影响Fig.11 Effect of noise on proposed method

图11b为对图11a包含噪声的肢体部分拟合的结果，可见在肢体边缘会产生不属于奶牛的多余点。图11e为对图11d所示存在噪声的腹部进行拟合的结果，拟合后的点云噪声点数增大。因此，在点云拟合前应先进行光顺和降噪处理。对图11a和图11d点云进行高斯滤波[16]，用本文方法进行拟合的结果如图11c和图11f所示，可见肢体边缘和腹部拟合效果得到改善，但由于采用统一的高斯滤波参数，仍存在肢蹄变细、腹部有少量噪声问题，故可利用局部平滑方法进一步改善。

4 结论

(1)提出了一种基于三次B样条曲线的奶牛点云较大缺失区域修复方法，参数h=1/4，L/dmin=5时，修复后的点列均匀性和逼近性能均优于三次B样条方法。

(2)对45头奶牛共225帧点云修复试验，结果表明，与三次B样条方法相比，本文方法平均帧逼近误差降低了26.7%，更加逼近原点云。

(3)在奶牛肢体和腹部存在噪声时，修复效果会受到较大影响，用高斯滤波进行光顺降噪后可以取得较好的平滑效果，但肢蹄变细、腹部仍存在少量噪声问题，需对局部光顺降噪算法做进一步研究。

1 李顺.中国畜牧业发展历程分析及趋势预测[J].中国畜牧杂志,2010,46(12):25-28.

LI Shun. Analysis on China livestock development process and trend forecast[J]. Chinese Journal of Animal Science,2010,46(12):25-28. (in Chinese)

2 刘长全, 杨洋.中国奶业产业政策的发展及成效[J].中国奶牛,2017(10):58-64.

3 莫佳蓓, 刘庆友.中国和日本奶牛养殖业规模化发展的比较分析[J].江苏农业科学,2017,45(9):303-307.

4 何东健, 刘冬, 赵凯旋.精准畜牧业中动物信息智能感知与行为检测研究进展[J/OL].农业机械学报,2016,47(5):231-244.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160532&flag=1.DOI:10.6041/j.issn.1000-1298.2016.05.032.

HE Dongjian, LIU Dong, ZHAO Kaixuan. Review of perceiving animal information and behavior in precision livestock farming[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(5):231-244. (in Chinese)

5 邵小宁.基于Kinect的植物三维点云获取与重建方法研究[D].杨凌:西北农林科技大学,2016.

SHAO Xiaoning. Research on 3D point cloud acquisition and reconstruction method of plant based on Kinect[D].Yangling:Northwest A&F University,2016. (in Chinese)

6 陈相, 童小华.基于三角格网的点云空洞修补算法及精度研究[J].测绘通报,2013(4):1-3.

CHEN Xiang, TONG Xiaohua. Research on points cloud hole filling algorithm and accuracy in triangle mesh[J]. Bulletin of Surveying and Mapping,2013(4):1-3. (in Chinese)

7 王果, 崔希民, 俞世炜, 等.应用扫描光线重建法的建筑立面遮挡点云恢复[J].测绘通报,2014(5):63-65.

WANG Guo, CUI Ximin, YU Shiwei, et al. Recovery of occluded building facade point cloud based on the reconstructed scan light and planar segmentation[J]. Bulletin of Surveying and Mapping,2014(5):63-65. (in Chinese)

8 WANG J, OLIVEIRA M M. Filling holes on locally smooth surfaces reconstructed from point clouds[J]. Image and Vision Computing, 2007, 25(1): 103-113.

9 CHALMOVIANSKY P, JUTTLER B. Filling holes in point clouds[J]. Lecture Notes in Computer Science, 2003, 2768: 196-212.

10 MARCHANDISE E, PIRET C, REMACLE J F. CAD and mesh repair with radial basis functions[J]. Journal of Computational Physics,2012, 231(5): 2376-2387.

11 NGO T M, LEE W S. Feature-first hole filling strategy for 3D meshes[M]. Springer Berlin Heidelberg, 2013: 53-68.

12 QUINSAT Y, LARTIGUE C. Filling holes in digitized point cloud using a morphing-based approach to preserve volume characteristics[J]. International Journal of Advanced Manufacturing Technology,2015, 81(1-4): 411-421.

13 蒋刚.基于SVM和空间投影的点云空洞修补方法[J].计算机工程,2009,35(22):269-271.

JIANG Gang. Point cloud hole filling method based on SVM and space projection[J]. Computer Engineering, 2009,35(22):269-271. (in Chinese)

14 晏海平,吴禄慎,陈华伟.基于径向基函数的散乱点云孔洞修复算法[J].计算机工程与设计,2014,35(4):1253-1257.

YAN Haiping, WU Lushen, CHEN Huawei. Hole repairing algorithm in scattered point cloud based on radial basis function[J]. Computer Engineering and Design,2014,35(4):1253-1257. (in Chinese)

15 RUSU R B, MARTON Z C, BLODOW N, et al. Towards 3D point cloud based object maps for household environments[J]. Robotics and Autonomous Systems,2008, 56(11): 927-941.

16 朱德海. 点云库PCL学习教程[M]. 北京: 北京航空航天大学出版社, 2012.

17 刘俊焱, 云挺, 周宇, 等.基于最小二乘的点云叶面拟合算法研究[J].西北林学院学报,2014,30(5):70-77.

LIU Junyan, YUN Ting, ZHOU Yu, et al. Leaf surface fitting of point cloud based on least square method[J]. Journal of Northwest Forestry University,2014,30(5):70-77. (in Chinese)

18 闫蓓, 王斌, 李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2008,34(3):295-298.

YAN Bei, WANG Bin, LI Yuan. Optimal ellipse fitting method based on least-square principle[J]. Journal of Beijing University of Aeronautics and Astronautics,2008,34(3):295-298. (in Chinese)

19 田垅, 刘宗田.最小二乘法分段直线拟合[J].计算机科学,2012,39(6A):482-484.

TIAN Long, LIU Zongtian. Least-squares method piecewise linear fitting[J]. Computer Science,2012,39(6A):482-484. (in Chinese)

20 苗莎, 郑晓薇.三次插值样条曲线拟合多核并行算法[J].计算机应用,2010,30(12):3194-3196.

MIAO Sha, ZHENG Xiaowei. Multi-core parallel algorithm for cubic spline curve fitting[J]. Journal of Computer Applications,2010,30(12):3194-3196. (in Chinese)

21 海啸, 朱志杰.最小二乘法和三次样条曲线拟合的比色测温误差修正对比分析[J].激光杂志,2015,36(6):72-76.

HAI Xiao, ZHU Zhijie. The comparison between the least square method and cubic spline interpolation in errors of colorimetry temperature measurement[J]. Laser Journal,2015,36(6):72-76. (in Chinese)

22 喻德生, 程程.基于离散曲率的三次均匀B样条的局部光顺算法[J].浙江大学学报:理学版,2011,38(5):511-517.

YU Desheng, CHENG Cheng. On local fairing algorithm for cubic B-spline with discrete curvature[J]. Journal of Zhejiang University:Science Edition,2011,38(5):511-517. (in Chinese)

23 韩江, 江本赤, 夏链, 等.基于轮廓关键点的B样条曲线拟合算法[J].应用数学和力学,2015,36(4):423-431.

HAN Jiang, JIANG Benchi, XIA Lian, et al. A B-spline curve fitting algorithm based on contour key points[J]. Applied Mathematics and Mechanics,2015,36(4):423-431. (in Chinese)

24 王文珂, 李思昆.无序B样条曲线的曲面拟合算法[J].计算机辅助设计与图形学学报,2013,25(5):679-685.

WANG Wenke, LI Sikun. B-spline surface fitting to unorganized curves[J]. Journal of Computer-Aided Design & Computer Graphics,2013,25(5):679-685. (in Chinese)

25 段振云, 王宁, 杨旭, 等.一种改进B样条曲线拟合算法研究[J].机械设计与制造,2016(5):17-19.

DUAN Zhenyun, WANG Ning, YANG Xu, et al. An algorithm of improved B-spline curve fitting[J]. Machinery Design & Manufacture,2016(5):17-19. (in Chinese)