高地隙喷雾机主动空气悬架减振控制与实验
2018-07-05武秀恒秦嘉浩杜岳峰宋正河
武秀恒 秦嘉浩 杜岳峰 宋正河 陈 雨 谢 斌
(1.中国农业大学工学院, 北京 100083; 2.现代农业装备优化设计北京市重点实验室, 北京 100083; 3.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100)
0 引言
近年来,随着自走式喷雾机向大功率、高地隙、宽喷幅方向发展,整机质心亦随之提高,喷杆长度显著增加。工作时车身较小的振动即可引起喷杆端部较大的位移变化,尤其在接近于悬架固有频率的地面条件下,车身振荡剧烈,加之喷杆与车身各自的振动形成耦合,严重影响喷药质量与行车安全。此时若增设减振性能优良的主动悬架,则能防止车身发生倾倒、提高喷药精度,还可改善乘坐舒适性、延长零部件寿命。
目前对空气悬架系统的研究多集中于半主动型式,因其结构简单、能耗低、便于维护且易于控制实施[1-5]。然而,主动空气悬架系统依靠外界动力输入连续调节悬架刚度,具有对恶劣环境适应性强的优点,大幅改善行驶平顺性和舒适性的同时,更能保证车辆的作业安全。此外,由于使用空气作为能量传递介质,其制造和维护成本较低,舒适性高,清洁环保且便于控制[6]。主动悬架较半主动悬架耗能高,但如只在上述特殊工况下适时开启,较高的能量消耗也因相对短的工作时间而可忽略。此外,由于农业装备慢速重载低频的特点,主动空气悬架恰能满足其响应速度。
主动悬架系统包括悬架机械结构与主动力实施部分(空气弹簧及其供气系统)。与机械结构的运行过程比较,空气弹簧的充放气过程具有较强的非线性,系统参数时变[7-10],传统线性控制器对系统性能的提升较为有限。另一方面,减振过程中不但要求在外部激励下车身加速度尽量小,还要求悬架位移尽可能保持在设定位置附近,以防减振过程中悬架位移偏移过大而造成车身侧倾,因此需要对车身加速度和悬架位移两个变量同时进行控制[11-12]。此外,在进行控制器设计时,还需充分考虑空气弹簧的压力调节范围,悬架行程约束以及减振过程中轮胎与地面间的接触力等[13-14]。
为解决大型高地隙喷雾机在复杂地面条件下,尤其处于地面激励接近于悬架固有频率这一特殊工况下的剧烈振动问题,本文提出适时开启的主动空气悬架减振方案。设计一种空气悬架H∞状态反馈与时频非线性联合减振控制策略。首先,以实时测量空气弹簧压力的传感器为节点,将主动悬架的控制问题分为两部分。基于LMI方法求解在约束条件下的H∞状态反馈控制器增益,该控制器将车身加速度、悬架位移等信息作为反馈进行综合,可保证多个变量的实时调整,由此计算当前时刻空气弹簧所需施加的主动力。针对空气弹簧充放气过程非线性,应用时频非线性控制方法加以处理。基于空气弹簧压力传感器的反馈,时频控制器实时调节比例电磁阀开度以控制空气弹簧时刻跟踪理想主动力的期望值。最后,依托室内1/4车辆主动空气悬架实验台,对所设计的减振方案进行实验验证。
1 主动空气悬架方案与动力学模型
主动空气悬架二自由度模型如图1所示。图中,ms、mu分别为簧载质量与簧下质量,ca、ct分别为悬架阻尼系数与轮胎等效阻尼系数,kt为轮胎等效刚度;xs、xu、xr分别为运动过程中的车身位移、轮胎位移以及由于地面起伏而产生的对悬架的输入位移,p1、V1为空气弹簧中气体绝对压力和体积,ps为供气压力,pa为放气时出口大气压力,V为控制器输出电信号。
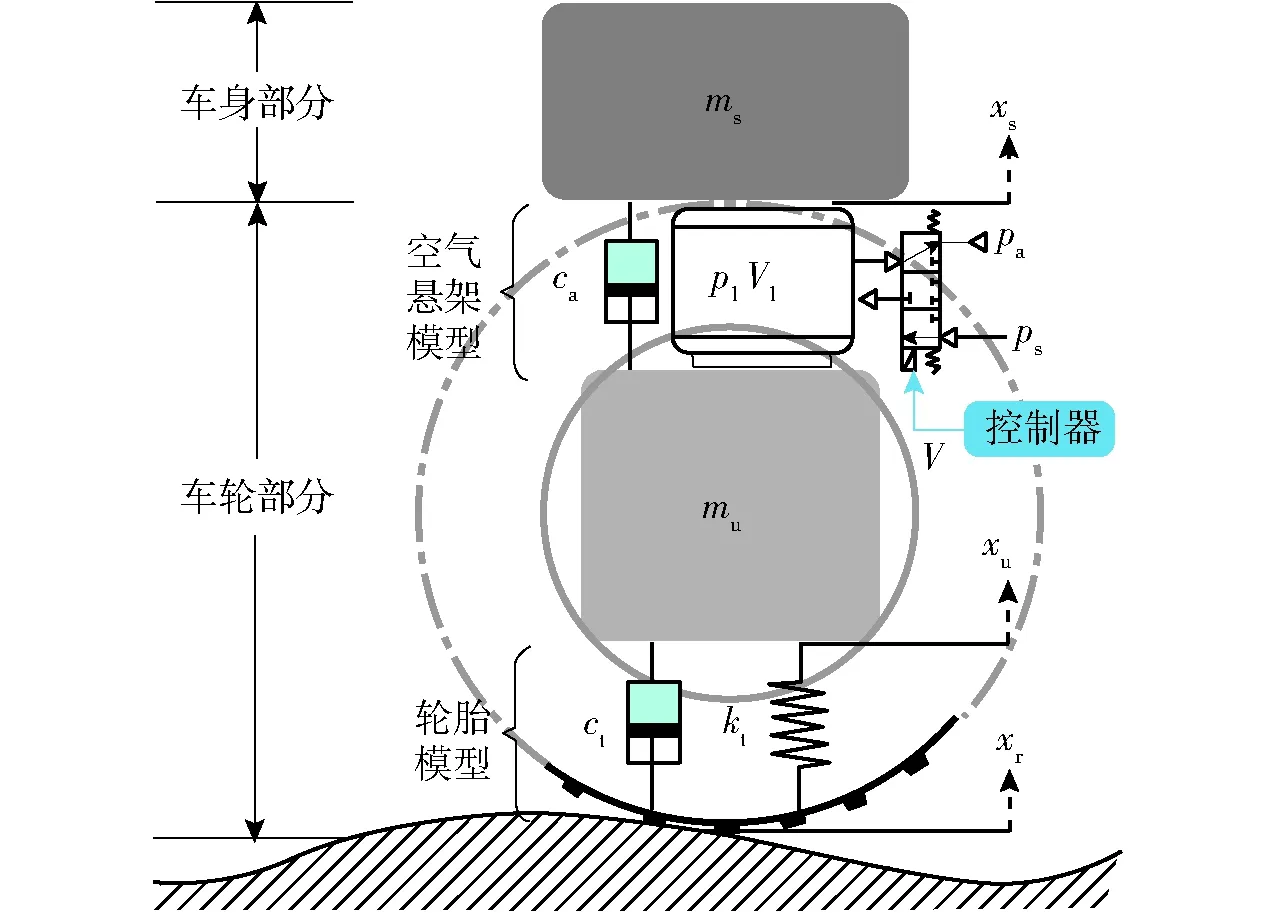
图1 带空气弹簧主动悬架二自由度模型Fig.1 Schematic of active pneumatic suspension
由图1可知,空气弹簧由三位五通比例集成电磁阀控制,当电磁阀处于中位时,切断了弹簧与外界气体的交换过程,此时整体相当于被动悬架;当喷雾机行驶于颠簸地面时,控制电磁阀开启,此时可对空气弹簧进行实时充放气,以调节弹簧刚度,达到主动悬架减振的目的。由于有针对性的开启与关闭主动控制,能够使悬架在保证喷雾机行驶平稳的同时,尽可能地减少能量消耗。
综合牛顿第二定律、气体状态方程与质量流量方程,可得主动空气悬架二自由度模型的微分方程为[14-16]
(1)
式中Ae——空气弹簧有效截面积,m2
n——气体绝热指数
R——气体常数
T0——空气弹簧中初始热力学温度,K
p0——空气弹簧中初始压力,MPa
G——质量流量,kg/s
通过调节比例电磁阀可切换空气弹簧的充放气过程和控制气体质量流量G,以此达到控制空气弹簧压力的目的。根据图1中电磁比例阀开合与弹簧充放气关系,质量流量G的计算公式为[16-17]

(2)
式中cd——节流阀孔流量系数
TU——节流阀孔上游空气温度,K
AK——比例电磁阀阀口面积,m2
AK与输入给电磁阀电压成一定关系,当AK>0时,表示空气弹簧充气过程,AK<0时,表示空气弹簧放气过程。
通过上述数学模型可知,空气弹簧的充放气过程具有不连续性,传递能量的介质——空气受环境影响大,整个空气弹簧压力控制系统参数时变,非线性较强。因此,针对线性化后的系统模型所设计的控制器对实际系统性能的提升较为有限,因此宜采用非线性控制方法。
以状态空间为设计基础的状态反馈线性控制器可同时控制系统多个状态变量,不同于空气弹簧的运动,悬架机械结构运动过程的非线性问题不是特别突出,基于此,应用状态反馈既满足了同时控制的要求,又能保证总体控制品质。综上,为了将状态反馈控制与非线性控制方法相结合,需对系统数学模型进行转换。考虑到压力传感器较流量传感器具有成本低、简单耐用、安装方便、响应频率较高且测量较精准,因此以空气弹簧中压力为节点,将主动悬架机械部分数学模型转换为状态空间形式。
选取状态变量为

由此得到以状态空间形式所表示的动力学模型为
(3)
其中

式中z(t)——车身垂向加速度控制输出
zc1(t)——悬架的行程限制控制输出
zc2(t)——轮胎动静载比值控制输出
xmax——空气弹簧行程限制
O——零矩阵
zc1(t)<1表示控制过程中弹簧的伸缩位移应小于设计的最大行程,以免发生悬架结构间的碰撞从而降低车身稳定性甚至造成零件损坏;此外,由式(3)状态方程可知,Ae作为重要参数指导状态反馈控制器的计算,而根据空气弹簧的特性,当弹簧在行程范围内伸缩时,有效截面积Ae几乎不变,一旦超过该限制,随着高度的变化其截面积Ae变化较大,因此超过限制后同样会降低状态反馈控制器的控制效果。进一步,为了保证操作稳定性和安全性,行驶过程中轮胎与地面间需要始终存在正压力,以保证可靠的轮胎附着力,即要求zc2(t)<1。最后,在整个控制过程中,空气弹簧中的压力不应超过供气压力,即控制输入需满足限制条件|u(t)|≤umax。
2 控制原理
基于以上分析,在综合考虑主动空气悬架机械部分的多变量控制与空气弹簧的非线性问题后,本文所确定的控制方案如图2所示。图中,向量x表示被控系统状态输出,xd为期望输出,K为状态反馈控制器增益向量,pd为由状态反馈控制器所计算的空气弹簧期望压力,p为压力传感器所测得系统实际压力。时频控制器内部包含有一比例控制,用于镇定系统,其中kp为比例系数。

图2 主动空气悬架控制方案Fig.2 Control scheme of active pneumatic suspension
2.1 H∞状态反馈控制器增益的LMI求解
H∞控制因具有较好的抑制外界扰动能力而被广泛应用于振动控制,其控制目的在于最小化由扰动至车身垂向加速度传递函数的最大奇异值。该奇异值愈小,扰动抑制能力愈强[18]。H∞条件下的状态反馈控制器增益向量可通过求解下述引理中LMI而得到,并且应用该方法的另一优点在于各个约束条件均可转化为相应的LMI,在求解控制器增益时一并进行考虑。

(1)在无扰动情况时,系统在控制器作用下渐近稳定。
(2)零初始状态开始,由路面扰动w(t)到车身垂向加速度z(t)的传递函数G(jω)的范数满足
‖G(jω)‖∞<γ
(3)当路面扰动能量小于wmax=ρ/γ2时,各约束条件zc1(t)<1、zc1(t)<1以及|u(t)|≤umax可以得到保证。其中ρ为系统最大扰动能量;umax为空气弹簧供气系统可提供的最大输出压力。
由此,控制器增益为
(4)
(5)
(6)
(7)
2.2 非线性时频控制原理
作为一种非线性控制器,时频控制强调控制作用不仅应在时域减小误差,更应在频域抑制系统的响应频宽,因而控制算法需要同时作用于系统的时频域。基于此,时频控制算法融合了小波变换时频多分辨率的优点,将主动噪声控制领域中的滤波型最小均方(FXLMS)算法与离散小波变换集成,由于这两种方法在实际操作中均以滤波的形式进行运算,使得此控制器较其他非线性自适应控制器形式紧凑,计算效率高。并且FXLMS算法本身作为时域非线性控制器,具有较强的自适应能力,所以结合了小波变换后在控制强非线性甚至混沌系统时仍然效果显著[19-22]。
时频控制器的结构原理如图3所示。其中,W1与W2分别为辨识滤波器与控制滤波器,各包含N个滤波系数,其定义为
W1(n)=[w1,0(n)w1,1(n) …w1,N-1(n)]T
(8)
W2(n)=[w2,0(n)w2,1(n) …w2,N-1(n)]T
(9)
辨识滤波器W1实时辨识及跟踪系统的动态性能,控制滤波器W2实时调整控制输出。阴影框中的T代表二进制离散小波变换的分解矩阵,根据Mallat塔式算法[23],该矩阵为由高、低通滤波系数组成的方阵[24]。

图3 时频控制器原理图 Fig.3 Schematic of time-frequency controller
另外,定义向量
X(n)=[x(n)x(n-1) …x(n-N+1)]T
(10)
U(n)=[u(n)u(n-1) …u(n-N+1)]T
(11)
(n)=[(n)(n-1) …(n-N+1)]T
(12)
式中x(n)——n时刻控制器参考输入
u(n)——控制输出
式(10)定义了参考输入向量X(n),其包含前N个时刻参考输入。同理,控制器输出向量U(n)包含前N个时刻的控制器输出信号,并且
(13)
(14)
对W1(n)、W2(n)中系数的更新通常以误差的最小均方为目标,采用最速下降法进行适时调整,即
W1(n+1)=W1(n)+μ1TU(n)f(n)
(15)
W2(n+1)=W2(n)+μ2T(n)e(n)
(16)
其中
e(n)=d(n)-y(n)
(17)

(18)
(19)
式中e(n)——n时刻控制误差
f(n)——n时刻辨识滤波器与实际系统输出间的辨识误差
d(n)——n时刻期望输出压力或称参考输出
y(n)——n时刻的系统实际输出

μ1、μ2分别为辨识滤波器和控制滤波器系数计算过程中的迭代步长,同时是控制器设计中的关键参数,因此需要反复调试以权衡系统的动态特性与稳定性。综上,时频控制属于闭环自适应控制,系统反馈间接调整控制器的参数,以误差最小均方为目标,逐渐将误差控制在一定范围内。
3 控制器参数设计与实验
3.1 控制器参数求解与设计
主动空气悬架实验系统相关参数见表1。
根据表1参数值,设ρ=0.5,应用Matlab求解式(4)~(7)中LMI,在最优化γ=15.8的情况下,可求得H∞状态反馈控制器增益为时频控制器设计过程中,一般根据系统非线性的复杂程度而选取滤波系数长度不同的小波,本文参考已有文献并经过仿真分析,最终确定选用db3小波滤波器,其高、低通滤波器分别包含6个滤波器系数[25-26]。
K=105×
[-2.170 3 -1.207 8 -0.714 8 -0.080 8]
对于系统辨识滤波器W1(n)以及控制滤波器W2(n),滤波器越长,采样频率越高,包含的参数越多,越能精确对系统进行估计和控制,但受限于控制器硬件的计算能力,为确保控制的实时性,选择滤波器的长度N=128,采样频率为1 000 Hz。

表1 主动空气悬架实验系统主要参数Tab.1 Main parameters of active pneumatic suspension test system
滤波器参数更新时的迭代步长属于时频控制器的关键参数,较大的迭代步长保证了控制器跟踪目标的快速性,使系统具有较快的响应速度,但降低了闭环系统的稳定性;相反,减小迭代步长有助于提升闭环系统稳定性。经过仿真与实际调试,得到较优的迭代步长为μ1=μ2=1×10-16。另外,在时频控制之前应首先使用比例控制镇定被控系统。
确定控制器参数后,对闭环系统的频响进行估计。通过计算线性化系统传递函数的最大奇异值,分别得到开环与闭环系统的幅频响应,如图4所示。当系统输入约为1.3 Hz时,开环系统出现一阶共振现象,簧载质量加速度幅值上升剧烈。如果喷雾机工作过程中某一车轮遇到类似地面激励,则整机大幅侧向摆动,喷杆端部很可能撞击地面,造成零部件损坏。而加入状态反馈后的闭环系统加速度幅值显著减小,说明在空气弹簧充放气控制理想的前提下,加入主动控制后的减振效果明显。此外,该结果可为后续实验过程中激励模式的确定提供参考。

图4 开环系统与闭环系统幅频响应Fig.4 Amplitude-frequency response of open and closed loop systems
3.2 仿真结果与实验验证

图5 主动空气悬架实验台架Fig.5 Photo of active pneumatic suspension test-bench1.振动实验台架 2.液压泵站 3.激振台主控制器 4.空气弹簧 5.激振液压油缸 6.悬架控制器
主动空气悬架室内实验系统如图5所示。实验中,充放气的控制由比例流量阀与电磁换向阀所集成的气路完成,如图6所示。比例流量阀为Teknocraft公司生产的隔离平衡阀(型号iQ203311),通过调节输入电压改变阀口开度以调节流量;换向阀采用SNACE公司4V330C-10型三位五通电磁阀,通过高低电平调节阀口开关实现充放气功能。控制器采用NI公司PXIe-8135实时控制系统,其优点在于可将Matlab中编辑的控制算法代码直接转换下载并实施,该控制系统配置了多达32路模拟输入输出,方便控制策略的实际验证。

图6 充放气及流量控制集成部件Fig.6 Integrated component for air flux control1.比例电磁阀 2.比例电磁阀驱动模块 3.电磁换向阀
为了考察主动空气悬架时域减振效果,对开环系统、半主动控制系统和主动控制系统分别进行了仿真与实验。其中半主动控制系统采用文献[16]中所设计的带有附加气室的空气弹簧减振方案,通过调节空气弹簧与附加气室之间阻尼孔通流面积改变悬架阻尼,以达到根据外界激励情况进行主动控制的目的。其中控制算法为基于天棚-地棚参考的混合滑模控制,作为半主动悬架控制中目前研究的热点方向,其控制效果较优。因此,与其对比可充分证明主动空气悬架的优良减振性能。
根据图4系统频响结果,为模拟喷雾机车轮行驶与接近悬架系统固有频率的工况,考虑1.3 Hz下的路面激励

在该扰动输入下,簧载质量加速度响应的仿真结果对比如图7所示。实验过程中控制液压油缸同样输出该激励,实验结果对比如图8所示。

图7 主动空气悬架控制仿真结果对比Fig.7 Comparison of simulation results for active pneumatic suspension

图8 主动空气悬架控制实验结果对比Fig.8 Comparison of experiment results for active pneumatic suspension
仿真与实验结果均表明,在H∞状态反馈与时频非线性联合控制作用下,主动悬架的减振效果明显。由于系统采样需要时间以及电磁阀等控制部件存在一定的反映滞后,导致实验效果较仿真效果系统性能稍有下降,但实验结果与仿真结果能较好地匹配,由此说明,H∞状态反馈控制器增益设计适当,时频非线性控制器能较好地处理实际过程中空气弹簧系统的非线性特征,使其发挥出较为理想的减振效能。由实验结果可知,在系统一阶共振频率的激励条件下,被动悬架簧载质量最大加速度达8.5 m/s2左右,半主动悬架的最大加速度约为7 m/s2,而主动空气悬架的最大加速度降低至2.5 m/s2;并在激振结束后迅速稳定系统,缩短了系统振荡时间。
图9为主动减振过程中因控制空气弹簧变形而产生的悬架位移的变化结果。可知,悬架位移在整个控制过程中始终处于悬架行程内,而当激励停止后,悬架位移恢复到零初始位置,进一步说明状态反馈控制在抑制加速度的同时,可缓慢调整悬架位移,防止在振动控制过程中较大程度的偏离初始位移。

图9 主动控制过程中悬架位移变化Fig.9 Vibration result of suspension displacement during control process
为进一步验证控制方案的有效性,围绕随机路面激励条件下的悬架减振效果进行了仿真与实验。基于国家标准对随机路面功率谱的定义,根据其中时域和频域的描述关系,应用Matlab/Simulink生成车速为15 km/h时F级路面的时域激励信号[16,27],其能够描述一类典型农田路面的不平度情况[28]。图10为计算产生的田间随机路面时域激励信号,显示了车速一定时,路面起伏程度随时间的变化情况。以此类信号作为激励模拟田间路面工况,控制前后仿真与实验结果分别如图11和图12所示。

图10 田间随机路面时域激励信号Fig.10 Road random excitation signal in time domain
由图11、12可知,当车速处于某一范围内,路面激励频率会在悬架固有频率附近波动。当激励频率接近悬架固有频率时,可致被动悬架车身部分的加速度在短时间内升高;而当激励频率远离悬架固有频率时加速度又随之降低。但仿真和实验结果均表明,在整个随机路面激励过程中,主动空气悬架开启后的车身加速度明显减小,再次证明了本文策略能有效降低车身的振动,保证整机的平稳运行。

图11 随机路面激励下控制前后仿真结果Fig.11 Simulation results under road random excitation

图12 随机路面激励下控制前后实验结果Fig.12 Experiment results under road random excitation
4 结论
(1)设计了适时开启的高地隙喷雾机主动空气悬架控制策略并进行了室内台架实验。在模拟该系统受一阶共振频率激励的工况下,被动悬架最大簧载质量加速度可达8.5 m/s2左右,半主动悬架的最大加速度约为7 m/s2,而主动悬架的最大加速度降至2.5 m/s2,并在激振结束后迅速稳定,明显缩短了系统振荡时间。田间随机路面激励工况下的实验同样显示出主动空气悬架显著的减振效果。表明所提出的H∞状态反馈与时频非线性联合控制策略可有效抑制车身的剧烈抖动,继而提升工作可靠性、安全性与乘坐舒适性。
(2)时频非线性控制器能够辨识空气弹簧系统的非线性并加以控制,使其准确地跟踪实时计算的期望压力,保证了主动减振控制成功的实施。H∞状态反馈控制器在满足限制条件以及减小车身加速度的同时,保证了悬架在初始设定位置附近振动,由此可确保车身在振动控制过程中的水平位姿。
1 NGUYEN V L, ZHANG J, LE V Q, et al. Performance analysis of air suspension system of heavy truck with semi- active fuzzy control[J]. Journal of Southeast University: English Edition, 2017,33(2):159-165.
2 SUN X, YUAN C, CAI Y, et al. Model predictive control of an air suspension system with damping multi-mode switching damper based on hybrid model[J]. Mechanical Systems and Signal Processing, 2017,94:94-110.
3 孙晓强, 陈龙, 汪少华, 等. 半主动空气悬架阻尼多模型自适应控制研究[J/OL].农业机械学报, 2015,46(3):351-357.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150351&flag=1. DOI:10.6041/j.issn.1000-1298.2015.03.051.
SUN Xiaoqiang, CHEN Long, WANG Shaohua, et al. Research on damping multi-model adaptive control of semi-active air suspension[J/OL]. Transactions of the Chinese Society for Agricultual Machinery, 2015,46(3):351-357.(in Chinese)
4 吴光强, 黄焕军, 叶光湖. 基于分数阶微积分的汽车空气悬架半主动控制[J/OL].农业机械学报, 2014,45(7):19-25.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140704&flag=1. DOI:10.6041/j.issn.1000-1298. 2014.07.004.
WU Guangqiang, HUANG Huanjun, YE Guanghu. Semi-active control of automotive air suspension based on fractional calculus[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014,45(7):19-25.(in Chinese)
5 TODKAR R G. Design, development and testing of an air damper to control the resonant response of a SDOF quarter-car suspension system[J]. Modern Mechanical Engineering, 2011, 1(2): 84-92.
6 张军. 轿车主动空气悬架系统3种方案仿真分析[J].北京理工大学学报, 2007, 27(9):779-782.
ZHANG Jun. Simulation analysis on three concepts of active air spring suspension system of passenger car[J]. Transactions of Beijing Institute of Technology, 2007,27(9):779-782.(in Chinese)
7 ZHU H, YANG J, ZHANG Y, et al. A novel air spring dynamic model with pneumatic thermodynamics, effective friction and viscoelastic damping[J]. Journal of Sound and Vibration, 2017, 408: 87-104.
8 ZARGAR B, FAHIM A, JNIFENE A. Development, validation, and parameter sensitivity analyses of a nonlinear mathematical model of air springs[J]. Journal of Vibration and Control, 2012,18(12): 1777-1787.
9 LIU H, LEE J C. Model development and experimental research on an air spring with auxiliary reservoir[J]. International Journal of Automotive Technology, 2011, 12(6): 839-847.
10 PORUMAMILLA H, KELKAR A G, VOGEL J M. Modeling and verification of an innovative active pneumatic vibration isolation system[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2008, 130(3): 031001-031001-12.
11 KIM H, LEE H. Height and leveling control of automotive air suspension system using sliding mode approach[J]. IEEE Transactions on Vehicular Technology, 2011, 60(5): 2027-2041.
12 RAJAMANI R. Vehicle dynamics and control[M]. New York:Springer Science & Business Media, 2011.
13 CHEN H, GUO K H. ConstrainedH∞control of active suspensions: an LMI approach[J]. IEEE Transactions on Control Systems Technology, 2005, 13(3): 412-421.
14 SUN W, GAO H, KAYNAK O. Adaptive back-stepping control for active suspension systems with hard constraints[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1072-1079.
15 ROBINSON W D. A pneumatic semi-active control methodology for vibration control of air spring based suspension systems[D]. Ames: Iowa State University, 2012.
16 陈雨. 高地隙喷雾机独立式立轴空气悬架设计方法与特性研究[D]. 北京:中国农业大学, 2017.
CHEN Yu. Research on design methods and characteristics of independent strut type air suspension system for high clearance sprayer[D]. Beijing: China Agricultural University, 2012.(in Chinese)
17 ZARGER B. Model development, validation and nonlinear control of pneumatic suspensions[D]. Ottawa: University of Ottawa, 2007.
18 GAO H, SUN W, SHI P. Robust sampled-dataH∞control for vehicle active suspension systems[J]. IEEE Transactions on Control Systems Technology, 2010, 18(1): 238-245.
19 LIU M K, SUH C S. Simultaneous time-frequency control of bifurcation and chaos[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(6): 2539-2550.
20 LIU M K, SUH C S. Synchronization of chaos in simultaneous time-frequency domain[J]. Applied Mathematical Modelling, 2013, 37(23): 9524-9537.
21 WANG X, SUH C S. Nonlinear time-frequency control of PM synchronous motor instability applicable to electric vehicle application[J]. International Journal of Dynamics and Control, 2016,4(4): 400-412.
22 WANG X, SUH C S. Precision concurrent speed and position tracking of brushed DC motors using nonlinear time-frequency control[J]. Journal of Vibration and Control, 2016,83(2):141-148.
23 MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE Transactions on Information Theory, 1992, 38(2): 617-643.
24 SUH C S, LIU M K. Control of cutting vibration and machining instability: a time-frequency approach for precision, micro and nano machining[M]. Hoboken:John Wiley & Sons, 2013.
25 DAUBECHIES I. Ten lectures on wavelets[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1992.
26 武秀恒, 杜岳峰, C STEVE Suh, 等. 一种基于时频控制方法的控制器设计与实验[J].控制理论与应用, 2017,34(3):329-336.
WU Xiuheng, DU Yuefeng, C STEVE Suh, et al. On the design and physical validation of a time-frequency controller[J]. Control Theory & Applications, 2017, 34(3): 329-336.(in Chinese)
27 陈杰平, 陈无畏, 祝辉, 等. 基于Matlab/Simulink的随机路面建模与不平度仿真[J].农业机械学报,2010,41(3):11-15.
CHEN Jieping, CHEN Wuwei, ZHU Hui, et al. Modeling and simulation on stochastic road surface irregularity based on Matlab/Simulink[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 11-15.(in Chinese)
28 徐竹凤, 薛新宇, 崔龙飞, 等. 农田地面振动谱的研究综述[J].中国农机化学报, 2016, 37(7): 251-255.
XU Zhufeng, XUE Xinyu, CUI Longfei, et al. Review on farmland ground vibration spectrum[J]. Journal of Chinese Agricultural Mechanization, 2016, 37(7): 251-255.(in Chinese)
