基于栈式自编码器的FTIR光谱识别

李四海 余晓晖(甘肃中医药大学信息工程学院 甘肃 兰州 730000)(甘肃中医药大学药学院 甘肃 兰州 730000)

0 引 言

傅里叶变换红外光谱技术是一种新型检测技术，具有信噪比高、重复性好及检测速度快等优点，已在农业、食品、石油化工、药物质量控制等领域得到广泛应用。在中药研究领域，运用FTIR光谱技术对中药材的真伪、种类和产地进行鉴别，快速测定中药材中有效成分的含量以及中药辅料的品质，对于实现中药产品质量的过程控制、保证中药产品药效的稳定具有重要意义。

FTIR光谱的波段区间为4 000～400 cm-1，光谱含有大量的波数变量，其定性分析主要包括光谱特征提取及分类模型的建立。对光谱进行有效的特征提取可以降低模型的复杂性，提高泛化能力。目前常用的特征提取方法大致可分为两类：主成分分析PCA(Principal component analysis)及模型集群技术[1]。文献[2]利用傅里叶变换红外光谱仪采集了不同食用油油烟烟气红外光谱数据，运用PCA对高维光谱进行降维，分别建立了BP神经网络和概率神经网络分类模型，有效实现了食用油油烟种类的识别。文献[3]利用傅里叶变换红外光谱结合偏最小二乘判别分析PLS-DA(Partial Least Squares Discriminant Analysis)对摩洛哥四种产地的橄榄油进行了准确分类。PCA是一种十分有效的光谱压缩方法，被广泛用于数据的预处理，但PCA需要人工选择主成分个数，且其提取的特征是原始变量的线性组合，不能有效表达波数变量的非线性特征。文献[4-5]分别基于模型集群技术中的随机蛙跳和竞争自适应重采样技术进行光谱波数变量选择，实现了光谱数据的降维。模型集群技术的基本思想是预先生成光谱波数种子变量，然后采用一定的随机搜索策略和评价准则将重要变量不断添加到种子变量，最终得到一个最优的变量子集，使该子集的分类代价最小。该类方法需要重复建立判别模型对变量子集的优劣进行评价，计算开销较大。

深度学习是机器学习领域的一个新的研究热点，近年来在语音识别、机器翻译、计算机视觉等应用中取得很大进展。传统的支持向量机、BP神经网络、PLS-DA等浅层学习方法依靠人工经验抽取样本特征，模型学习后得到的是没有层次结构的单层特征。深度学习能够学习得到原始信号的层次化特征，有利于分类及数据特征的可视化[6]。目前，深度学习在中药光谱分析方面的应用还报道较少，文献[7]使用深度信念网络对太赫兹光谱进行识别，结果显示基于堆叠受限玻尔兹曼机的特征提取方法其分类性能最优。

针对现有的基于PCA及模型集群技术的光谱特征提取无法有效表达光谱的深层次及非线性特征，本文基于傅里叶变换红外光谱技术，利用栈式自编码器的逐层特征提取能力，挖掘光谱数据的深层次特征，建立传统中药材秦艽的分类模型，实现对秦艽光谱的有效识别。

1 栈式自编码

1.1 稀疏自编码

图1 自编码器

当隐藏层神经元个数小于输入层神经元个数时，AE能够得到输入数据的压缩表示。特别是对于存在多重相关性或较大冗余性的数据，AE能够学习到数据的潜在特征，得到数据的抽象表示，实现对数据的低维表达。

对n个样本进行分类的代价函数为[11]：

(1)

式中：代价函数的第一项为基本误差项，目的在于最小化重构误差；第二项为正则项，通过最小化所有权重参数的平方和能够对权重参数的解空间进行有效压缩，限制出现幅度较大解，防止过拟合，提高泛化能力。其中，xi和yi分别表示第i个样本的输入和输出值。nl为网络总层数、sl和sl+1分别为第l和l+1层的神经元数。Wji(l)为第l层第i个神经元和l+1层第j个神经元之间的连接权重。λ为权重衰减参数，用于控制惩罚项在代价函数中的相对重要性。

当隐藏层神经元数量较多时，通过对其施加稀疏性限制，使神经元大多数时间都处于被抑制的状态，从而能更有效地表达数据的特征。在代价函数中增加稀疏惩罚项，则总的代价函数为：

(2)

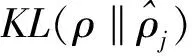
(3)

当ρj=ρ时，相对熵为0，因此最小化惩罚项能够使隐藏层的平均活跃度接近ρ。

在2013年12月13日召开的中国水利企业协会五届理事会二次会议上，新兴铸管股份有限公司被授予“2011—2012年度全国优秀水利企业”荣誉称号。

1.2 栈式自编码分类模型

栈式自编码器SAE 是一个由多层稀疏自编码器堆叠而成的深度神经网络，通过将最后一个隐藏层的输出与softmax分类器相连，构成SAE分类模型。包含两个隐藏层的SAE分类模型如图2所示。

图2 栈式自编码神经网络

训练SAE分类模型的关键是使用合适的无约束优化算法求解网络参数，包括权重参数和softmax分类器参数。对于深层神经网络，如果使用基于参数随机初始化的梯度下降算法进行训练，由于反向传播的梯度在靠近输入层时会急剧下降，出现梯度弥散，导致深层网络退化为浅层网络，不能有效地实现逐层特征提取[12-13]。因此，对于深层神经网络，一般采用逐层贪婪训练的方法进行，与参数随机初始化相比，逐层贪婪训练能够获得一个更好的网络参数初始值，减小网络参数陷入局部极小的可能性，加快监督训练阶段的收敛速度[14]。SAE分类模型的训练包括两个步骤：逐层贪婪训练和网络微调。

1.2.1 逐层贪婪训练

逐层贪婪训练[15]每次只训练网络中的一层，首先训练第一个隐藏层的网络参数，将该层的输出作为下一层的输入继续训练第二个隐藏层的网络参数，重复以上步骤直到完成所有自编码器的训练，最后用学习到的高层特征训练softmax分类器。

自编码器参数的训练步骤为：

(1) 计算输入的前向传播：

z(l+1)=W(l)a(l)+b(l)

(4)

a(l + 1)=1/(1 + e-z(l + 1))

(5)

式中:z(l)表示第l层的输入加权和，a(l)为该层的激励输出。

(2) 计算隐藏层各节点的残差：

δi(3)=-(yi-ai(3))f′(zi(3))

(6)

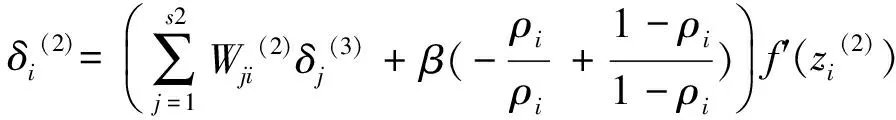
(7)

(3) 根据残差计算需要的偏导数：

▽W(l)J(W,b)=δ(l+1)(a(l))T

(8)

▽b(l)J(W,b)=δ(l+1)

(9)

softmax分类器的参数训练采用有监督的方式，具体步骤为：

(1) 首先计算分类器的总代价：

(10)

式中:第一项为误差基本项，第二项为权重衰减惩罚项。n为样本数，k为类别数，ξ为权重衰减项的惩罚系数，通过引入权重衰减项，代价函数变为了严格的凸函数，LBFGS算法(Limited-memory BFGS)可以较快地收敛到全局最优解。

(2) 计算分类器参数的梯度：

(11)

1.2.2 网络微调

逐层贪婪训练得到的网络参数值只是相邻两层之间的最优参数，要得到全局最优参数还需要对预训练得到的网络参数进行微调。具体方法为：根据逐层贪婪训练得到的网络参数，对输入进行前向传播，根据分类器的输出误差，按照式(11)微调分类器参数；将残差反向传播，按照式(8)和式(9)依次调整各隐藏层的权重和偏置，通过反复迭代直到获得网络的全局最优参数。

2 基于SAE的光谱识别

2.1 实验数据及预处理

实验平台为MATLAB R2016b，SAE及PLS-DA模型算法均通过编程实现。

秦艽样本分别采自甘肃古浪、天祝、卓尼等地，共144个，其中麻花秦艽68个，大叶秦艽76个。选取84个作为训练样本，60个作为测试样本。利用ALPHA-T型傅里叶变换红外光谱仪扫描得到所有样本的傅里叶变换红外光谱，光谱扫描范围为4 000～400 cm-1，每个样本包含2 558个波数变量。

为消除基线漂移及背景噪声的影响，对原始光谱数据进行基线校正及平滑预处理，采用三阶Savitsky-Golay平滑滤波，窗口大小为13。两种秦艽的原始平均光谱如图3所示。

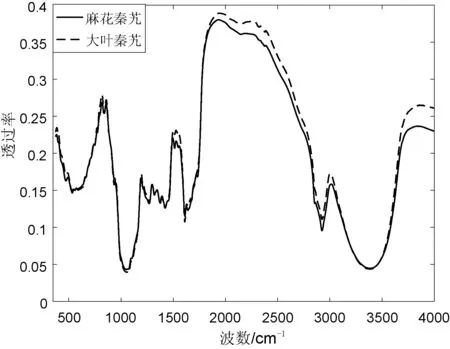
图3 两种秦艽的FTIR平均光谱

为更有效地求解神经网络，加快网络收敛速度，对光谱数据进一步进行归一化处理。

(12)

2.2 实验结果及分析

2.2.1 网络结构及参数设置

深度网络的结构设计目前尚没有通用的方法，要结合具体应用和数据特点进行设计。通常情况下，网络层数越多，通过逐层特征提取，网络的更高层越能提取到数据更抽象的特征，这些特征也能更好地表达数据的本质。但网络层数越多，需要优化的网络参数越多，网络学习时间也越长。考虑到FTIR光谱一维信号的特点，2个隐藏层就能够有效提取光谱信号的层次特征，因此确定隐藏层层数为2个。

网络中的其他参数对网络性能也有较大影响。本文通过实验，最终确定的网络参数见表1。

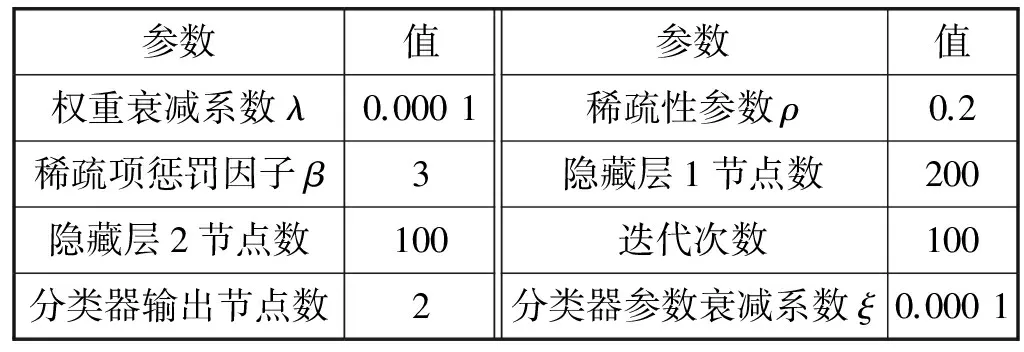
表1 网络参数

2.2.2 结果及分析

根据以上网络参数建立栈式自编码分类模型，使用LBFGS算法对权重参数及分类器参数进行优化。表2给出了网络预训练阶段，各隐藏层及softmax分类器的代价函数值及参数优化时间，图4是分类器总代价及权重衰减项的收敛曲线。

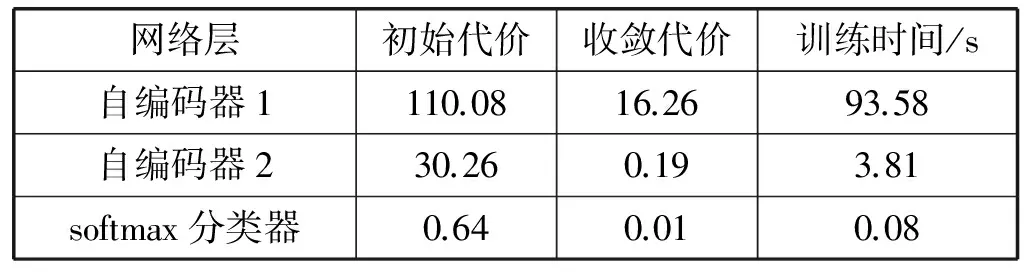
表2 网络代价及收敛时间

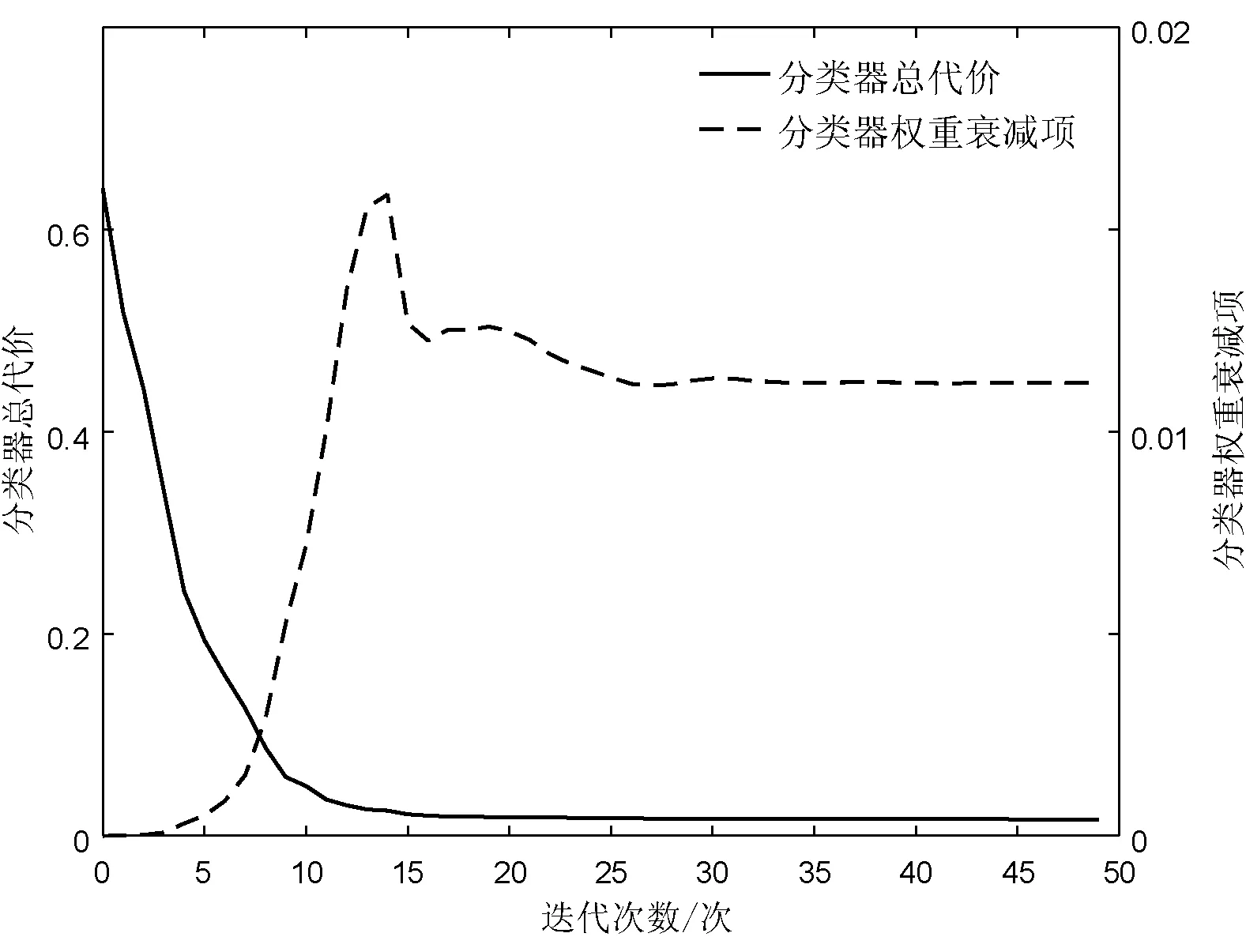
图4 softmax分类器代价函数收敛曲线

由表2可知：第一个隐藏层训练速度较慢，表明从原始数据提取特征最为复杂，提取到的是光谱的初级特征，而训练第二个隐藏层所需时间则明显减少，说明第一个隐藏层提取的特征是有效的。根据逐层提取的数据特征，softmax分类器的初始代价及收敛代价都非常小，这表明逐层贪婪训练有效地捕获了光谱信号的层次化特征。从图4可以看出，随着权重衰减项的快速增加，分类器总代价快速下降，迭代20次时已经收敛。权重衰减项在迭代的开始阶段快速上升的原因在于此时基本误差项较大，权重惩罚项的作用相对较小，当基本误差减小到一定程度时，权重惩罚项在总代价中的作用开始上升，因此权重惩罚项曲线开始下降，并在迭代30次左右时也趋于收敛，表明分类器最优参数的训练已经完成。

为说明本文方法的有效性，使用相同的训练集和测试集，分别建立FTIR光谱的PLSDA模型、深度信念网络(DBN-NN)模型以及基于竞争自适应重采样CARS(Competitive adaptive reweighted sampling)变量选择的PLSDA模型，对不同模型的分类性能进行对比。PLSDA模型通过对光谱进行主成分分析，提取前5个主成分，此时对原始光谱的方差解释水平为98.7%。使用提取的主成分建立PLSDA模型对两种秦艽进行分类。DBN-NN模型经过实验确定的参数为：两个RBM层，各隐层节点数为100、80，输出层节点数为2，批大小(batchsize)为14，网络预训练及权值微调学习率均为0.001，迭代次数分别为30、100。模型集群技术方法中，由于CARS算法变量选择效果好，速度较快，因此选择CARS算法进行变量选择，采样次数2 000次，5折交叉验证，模型集群中分类准确率最高的模型包含51个重要变量，根据选择的变量建立PLSDA模型，取前6个主成分。各分类模型在测试样本上的性能对比见表3。

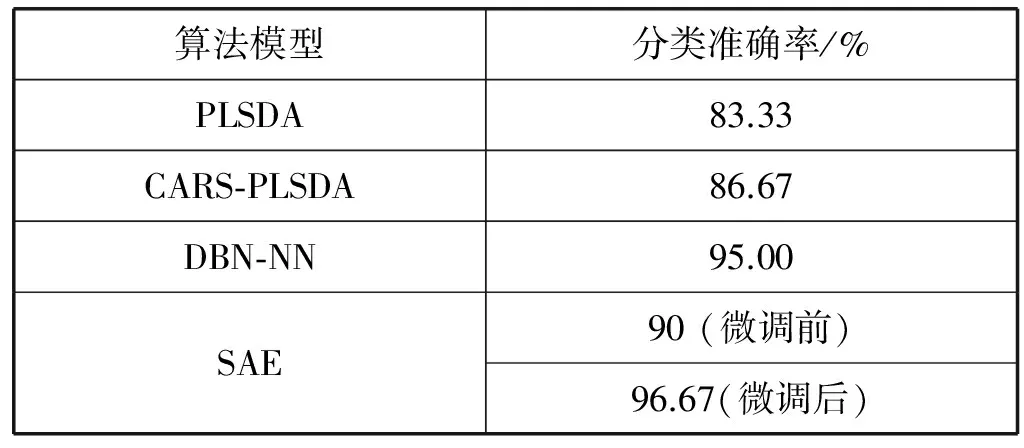
表3 不同模型的性能对比

从表3可知，与PLSDA相比，CARS-PLSDA通过变量选择提高了模型的泛化能力。基于深度学习的SAE及DBN-NN模型的分类准确率均高于PLSDA及CARS-PLSDA，DBN-NN的准确率与SAE接近，这表明深度学习能有效提取光谱信号的层次化特征，多层非线性结构具有强大的特征表达能力。其中，栈式自编码器在微调前的分类准确率也高于PLSDA及CARS-PLSDA模型，说明SAE具有更好的特征提取能力，能够有效挖掘光谱数据的深层次特征。对比网络微调前后的分类性能，可以看到微调可以对网络参数进行整体优化，改善网络性能，进一步提高模型的分类准确率。

3 结 语

采样栈式自编码器构建了FTIR光谱的softmax分类模型，网络的多层结构能够有效提取光谱数据的非线性及层次化特征，提高对光谱数据的抽象及表达能力。逐层贪婪训练能够找到更好的网络参数初始值，减小网络参数陷入局部极小的可能性，加快监督训练阶段的收敛速度。网络微调能够进一步优化整个网络的参数，对于提高分类性能有重要作用。FTIR光谱的识别对于中药质量控制具有重要意义，基于深度学习的光谱识别技术在海量光谱的快速鉴别中具有较为广阔的应用前景。

[1] Deng B C, Yun Y H, Liang Y Z. Model population analysis in chemometrics[J]. Chemometrics & Intelligent Laboratory Systems, 2015, 149:166- 176.

[2] 叶树彬，徐亮，李亚凯，等．基于人工神经网络的傅里叶变换中红外光谱法对食用油油烟种类识别研究[J]．光谱学与光谱分析，2017，37(3)：749- 754.

[3] Hirri A, Bassbasi M, Platikanov S, et al. FTIR spectroscopy and PLS-DA classification and prediction of four commercial grade virgin olive oils from morocco[J]. Food Analytical Methods, 2016, 9(4): 974- 981.

[4] 陈晓辉，黄剑，付云侠，等．基于iPLS和CARS数据融合技术的波长选择算法[J]．计算机工程与应用，2016，52(16)：229- 232.

[5] 郑剑，周竹，仲山民，等．基于近红外光谱与随机青蛙算法的褐变板栗识别[J]．浙江农林大学学报，2016，33(2)：322- 329.

[6] 尹宝才，王文通，王立春．深度学习研究综述[J]．北京工业大学学报，2015，41(1)：48- 59.

[7] 马帅，沈韬，王瑞琦，等．基于深层信念网络的太赫兹光谱识别[J]．光谱学与光谱分析，2015，35(12)： 3325- 3329.

[8] Bengio Y, Courville A, Vincent P. Representation learning: a review and new perspectives[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 35(8):1798- 1828.

[9] Baldi P, Guyon G, Dror V, et al. Autoencoders, unsupervised learning, and deep architectures Editor:I[C]// ICML Unsupervised and Transfer Learning, 2012: 37- 50.

[10] Schmidhuber J. Deep learning in neural networks: an overview[J]. Neural Networks, 2015, 61:85- 117.

[11] 王知音，禹龙，田生伟，等．基于栈式自编码的水体提取方法[J]．计算机应用，2015，35(9)：2706- 2709.

[12] 寇茜茜，何希平．基于栈式自编码器模型的汇率时间序列预测[J]．计算机应用与软件，2017，34(3)：218- 221.

[13] 段宝彬，韩立新，谢进．基于堆叠稀疏自编码的模糊C-均值聚类算法[J]．计算机工程与应用，2015，51(4)：154- 157.

[14] 陈国定，姚景新，洑佳红．基于堆栈式自编码器的尾矿库安全评价[J]．浙江工业大学学报，2015，43(3)：326- 331.

[15] Larochelle H. Greedy layer-wise training of deep networks[J]. Advances in Neural Information Processing Systems, 2007, 19:153- 160.