扩散式样条最小四阶矩算法

周 楠 倪锦根(苏州大学电子信息学院 江苏 苏州 215006)

0 引 言

将节点分布在特定的区域内，且每个节点跟邻域内的其他节点存在信息交换的网络可称为分布式网络[1]。分布式网络在回声消除、目标定位、生物群体活动建模和图像传感器网络等领域具有重要作用。自适应网络是指能够根据网络节点分布情况进行训练和自学习，并自适应地调节自身参数的分布式网络[2]。分布式估计算法通常用来对自适应网络的某些感兴趣参量进行估计。

分布式估计算法在信号处理领域应用广泛。近年来提出了几种分布式估计算法，如扩散式符号误差最小均方算法(DSE-LMS)[3]、分布式仿射投影符号算法(DAPSA)[4]、分布式子带自适应滤波算法(DSAF)[5]、分布式符号子带自适应滤波算法(DASAF)[6-7]、分布式最小四阶矩自适应算法(DLMF)[8]等。对于线性未知系统，上述分布式估计算法能够获得很好的性能，但是当未知系统的期望信号存在非线性失真时，上述算法的稳态失调较大。为了解决这一问题，文献[9]提出了扩散式样条最小均方算法(简记为DSLMS)，该算法对高斯噪声环境中的自适应网络具有较好地估计性能。然而，当网络中存在一些非高斯的大方差加性噪声时，算法产生的稳态失调较大。

本文首先定义节点误差的p阶矩代价函数，然后通过随机梯度法来最小化该代价函数，从而推出一般形式的扩散式样条自适应算法。当p为4时，可得扩散式样条四阶矩算法。仿真结果表明，与扩散式样条最小均方算法，该算法对均匀和二元噪声等功率较大的非高斯环境噪声具有更低的稳态失调。

1 分布式网络模型

自适应网络的节点连接方式可以用网络拓扑结构来表示。常用的自适应网络连接方式主要有递增式、扩散式和概率分布式三种[1]。在递增式拓扑结构中，每个节点包含的信息必须按顺序从一个节点传递到与之相邻的下一个节点，最终形成一个闭合的通信环；在扩散式拓扑结构中，每个节点与其邻域内的多个节点进行通信；在概率分布式拓扑结构中，每个节点是以一定的概率相连接，同样地与邻域内的节点进行通信。目前，扩散式拓扑结构应用最为广泛，本文算法也采用扩散式拓扑结构。

如图1所示的扩散式网络，各节点通过信息传递和自适应迭代的方式对包含N个节点的网络中的未知向量wo进行估计。节点k在n时刻的输入向量为xk,n=[xk(n),xk(n-1),…,xk(n-M+1)]T，其中M表示滤波器的抽头系数。在包含非线性失真的自适应网络中，期望信号可以表达为:

(1)

式中：νk(n)表示节点k受到的环境噪声，f(·)表示非线性失真函数。

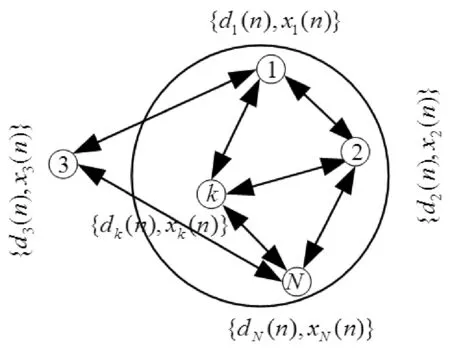
图1 扩散式拓扑结构

2 算法推导

在扩散式样条算法中，每个节点采用一个样条自适应滤波器，其结构框图如图2所示[10-11]。

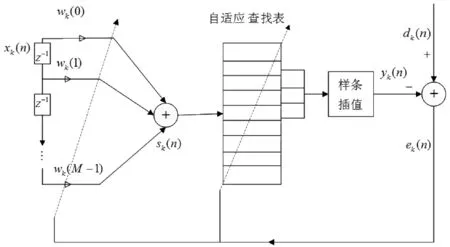
图2 扩散式网络节点采用的样条自适应滤波器框图

采用扩散式样条算法对未知系统进行估计时，在节点k先将输入信号通过自适应滤波器，得到线性输出为[10]：

(2)

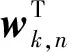
(3)

(4)

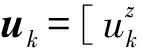
(5)

式中:B是样条基矩阵[12]。定义误差信号的p阶矩为:

(6)

对第k个节点的n时刻抽头系数向量求导可得:

(7)

(8)

对第k个节点的n时刻控制点向量qk,i,n求梯度可得:

(9)

(10)

研究表明，扩散式自适应网络使用“自适应-联合”(ATC)策略能够获得更低的稳态失调[1]。将ATC策略和最速下降法应用于样条自适应滤波器，可得:

(11)

(12)

(13)

(14)

以上两式为扩散式样条最小四阶矩(DSLMF)算法权值向量和控制点向量的迭代公式。

3 仿真实验

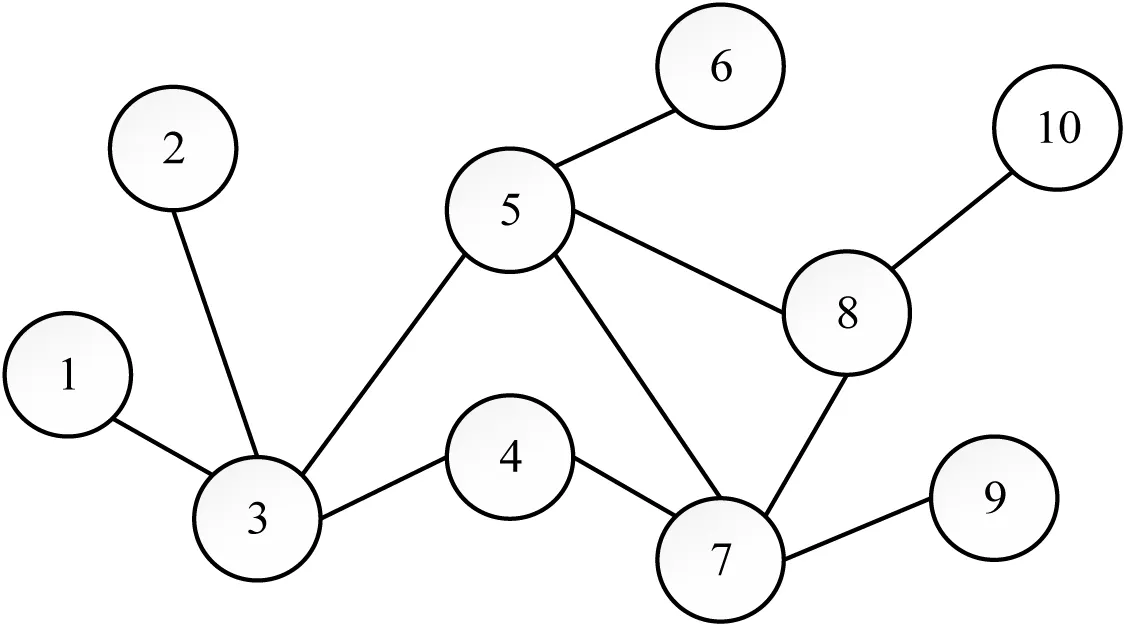
图3 扩散式的网络拓扑结构

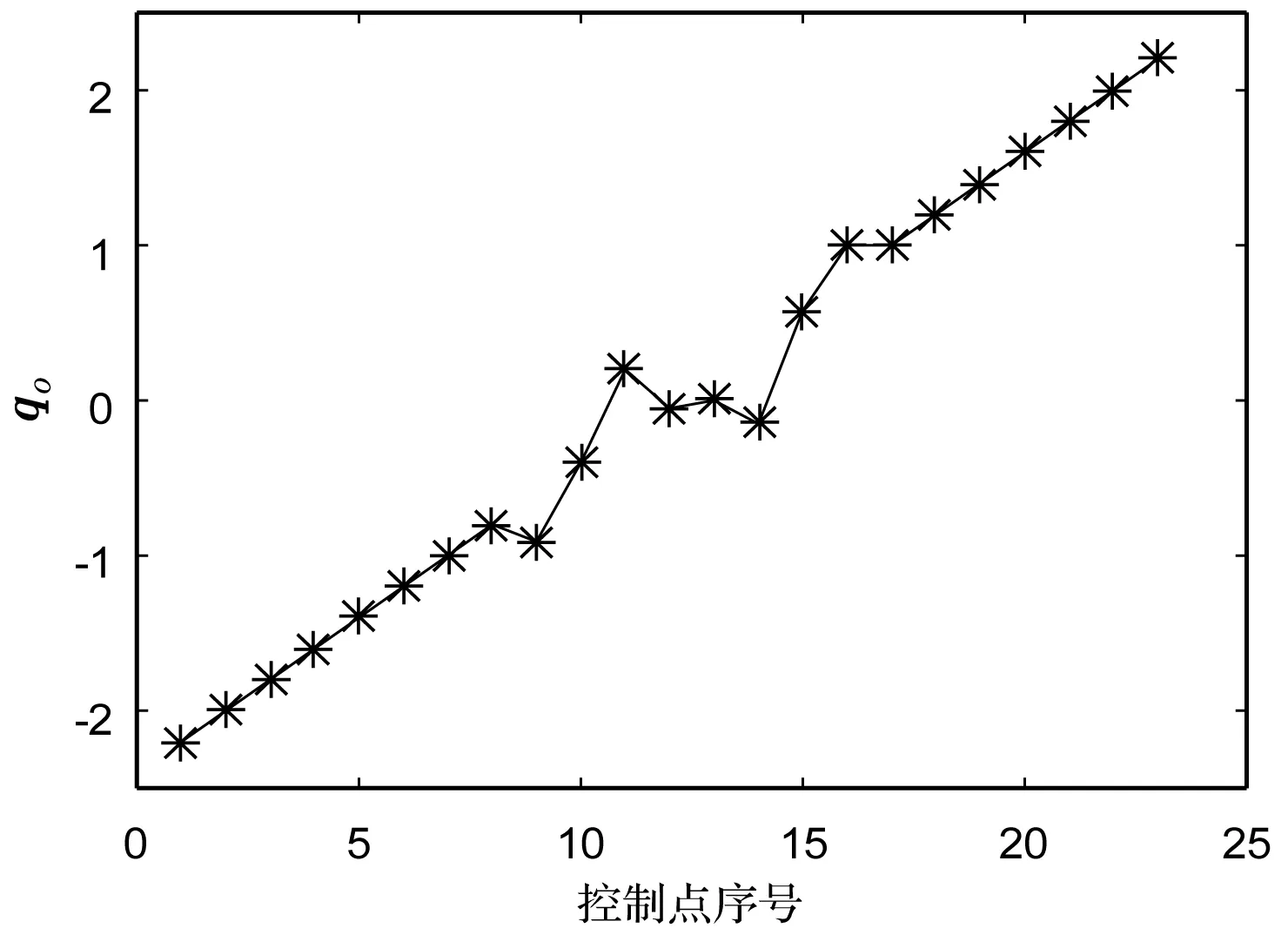
图4 未知控制点分布情况

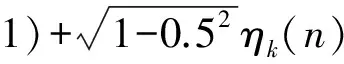
图5 节点输入信号、均匀噪声和二元噪声的方差

以白噪声作为输入，均匀噪声和二元噪声作为环境噪声的情况下，DSLMF和DSLMS的网络均方偏差曲线分别如图6和图7；为了在相同收敛速度条件下比较失调问题，步长分别取为0.002和0.000 02，图7中DSLMS和DSLMF的步长分别取为0.002和0.000 015。

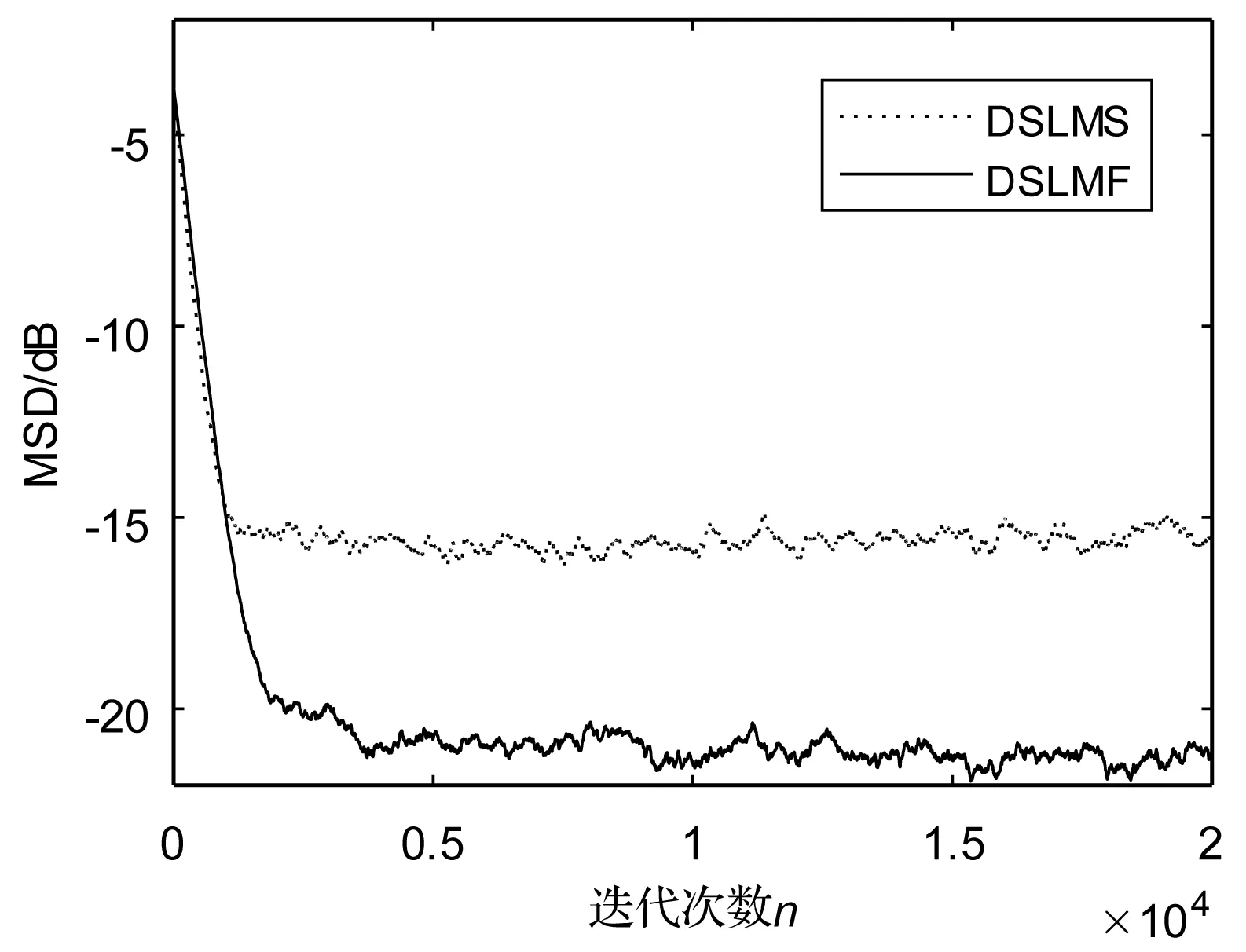
图6 DSLMS和DSLMF的网络均方偏差曲线，输入信号为白噪声，环境噪声为均匀加性噪声

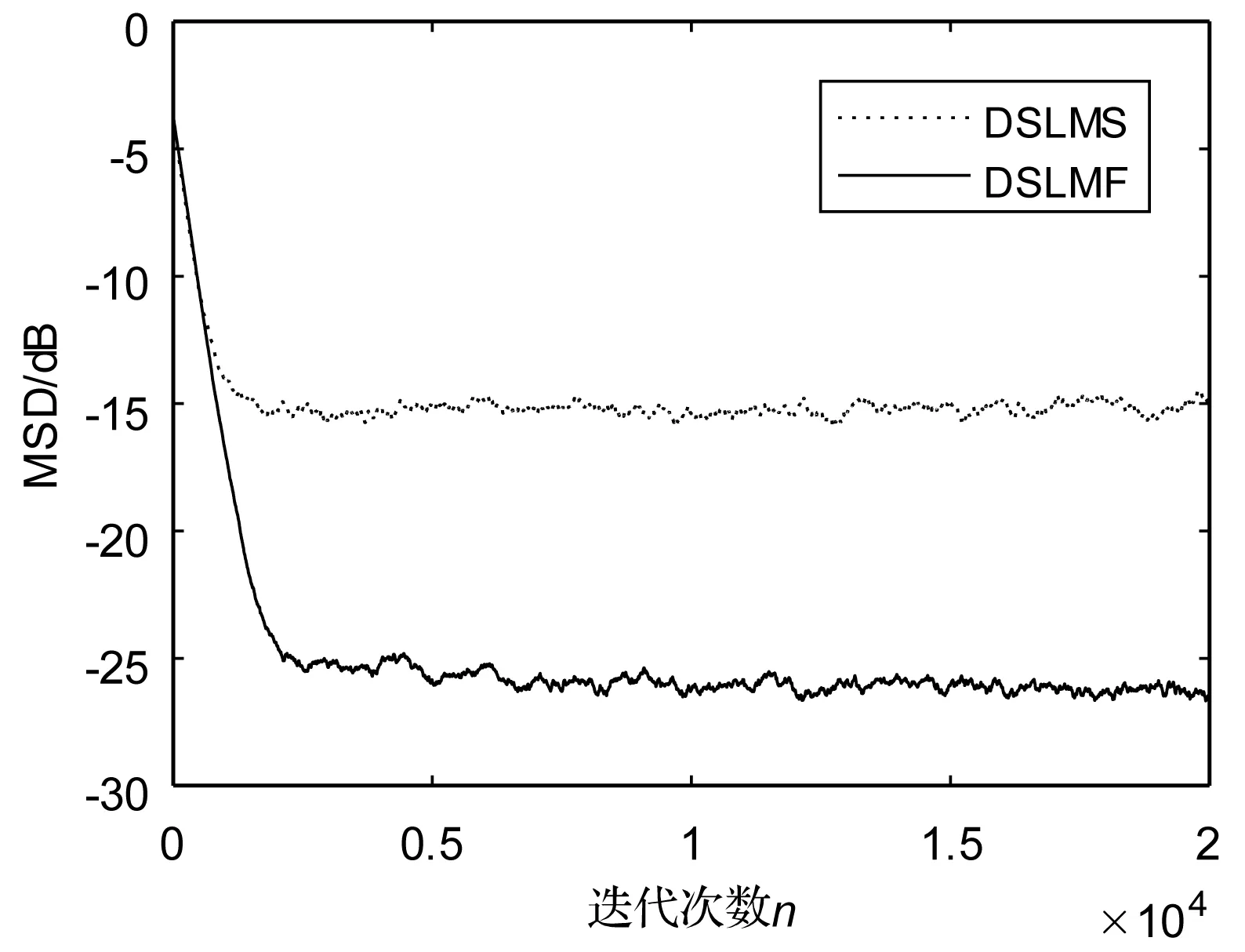
图7 DSLMS和DSLMF的网络均方偏差曲线，输入信号为白噪声，环境噪声为二元加性噪声

从图6和图7可以看出，无论是均匀还是二元环境噪声，DSLMF都比DSLMS具有更低的稳态失调。图8和图9将输入信号换成有色信号。由图可见，在有色信号输入下，DSLMF算法在较大的均匀或二元噪声干扰下，其稳态失调仍然优于DSLMS算法。

图8 DSLMS和DSLMF的网络均方偏差曲线，输入信号为有色，环境噪声为均匀加性噪声

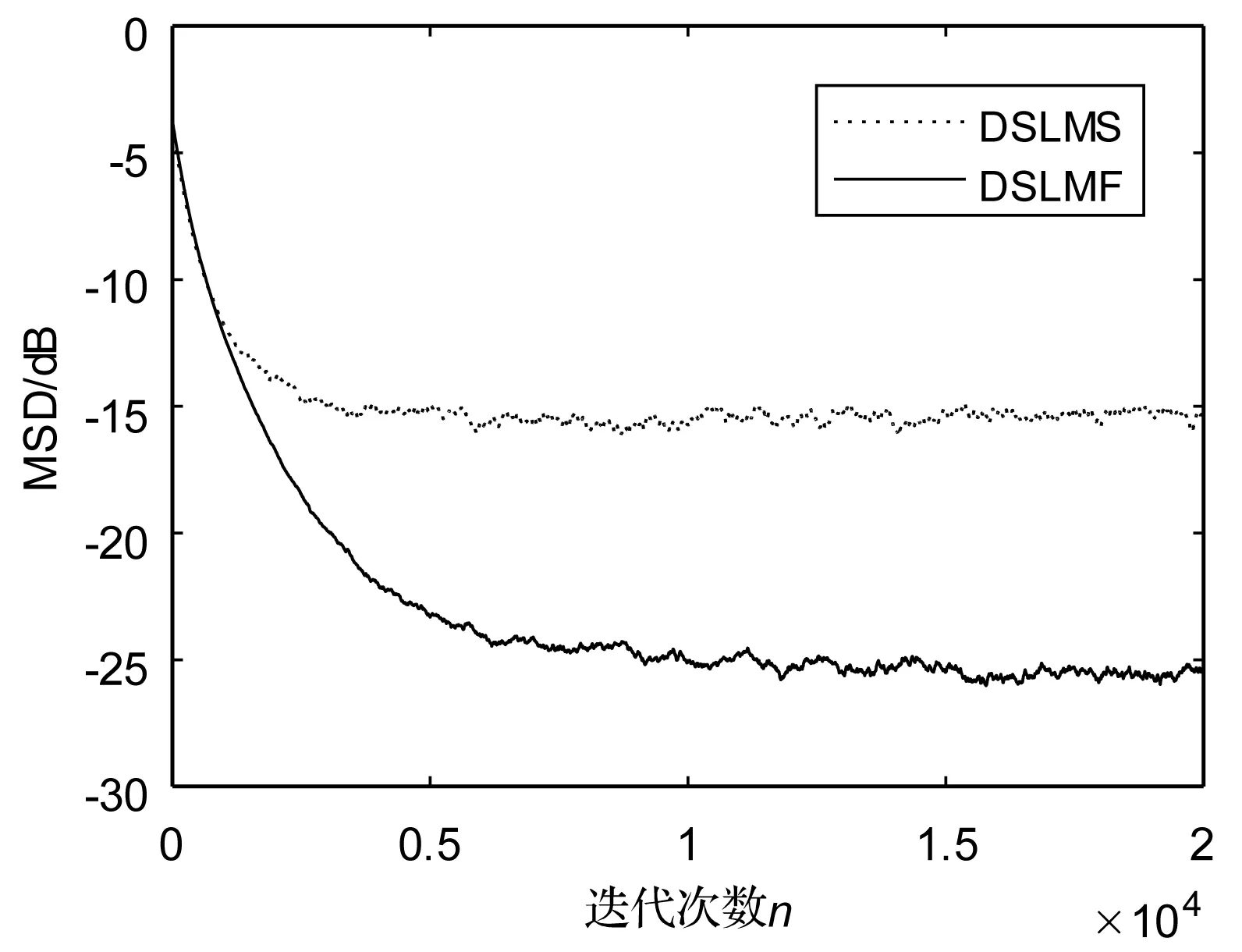
图9 DSLMS和DSLMF的网络均方偏差曲线，输入信号为有色，环境噪声为二元加性噪声

4 结 语

本文通过最小化p阶矩代价函数，运用梯度下降法，推出了一种扩散式样条自适应算法。当p取不同的整数时，可得到不同的算法。仿真结果表明，在较大的均匀噪声或二元噪声环境中，采用扩散式样条最小四阶矩算法具有很低的稳态失调。

[1] Sayed A H.Adaptive networks[J].Proceedings of the IEEE,2014,102(4):460- 497.

[2] Sayed A H.Adaptation,learning,and optimization over networks[J].Foundations and Trends in Machine Learning,2014,7(4- 5):311- 802.

[3] Ni J,Chen J,Chen X.Diffusion sign-error LMS algorithm:Formulation and stochastic behavior analysis[J].Signal Processing,2016,128:142- 149.

[4] 倪锦根,马兰申.抗脉冲干扰的分布式仿射投影符号算法[J].电子学报,2016,44(7):1555- 1560.

[5] 倪锦根,马兰申.分布式子带自适应滤波算法[J].电子学报,2015,43(11):2225- 2231.

[6] Ni J.Diffusion sign subband adaptive filtering algorithm for distributed estimation[J].IEEE Signal Processing Letters,2015,22(11):2029- 2033.

[7] Shi J,Ni J.Diffusion Sign Subband Adaptive Filtering Algorithm with Enlarged Cooperation and Its Variant[J].Circuits Systems & Signal Processing,2016,36(4):1- 11.

[8] Ni J,Yang J.Variable step-size diffusion least mean fourth algorithm for distributed estimation[J].Signal Processing,2016,122(C):93- 97.

[9] Scardapane S,Scarpiniti M,Comminiello D,et al.Diffusion spline adaptive filtering[C]//European Signal Processing Conference.IEEE,2016:1498- 1502.

[10] Scarpiniti M,Comminiello D,Parisi R,et al.Nonlinear spline adaptive filtering[J].Signal Processing,2013,93(4):772- 783.

[11] Guan S,Li Z.Normalised spline adaptive filtering algorithm for nonlinear system identification[J].Neural Processing Letters,2017,46(2):595- 607.

[12] Scarpiniti M,Comminiello D,Scarano G,et al.Steady-state performance of spline adaptive filters[J].IEEE Transactions on Signal Processing,2016,64(4):816- 828.