智慧旅游中基于语义轨迹的高效最近邻查询方法研究

孙一格 马 昂 吴 雷, 潘 晓 郭景峰(石家庄铁道大学经济管理学院 河北 石家庄 05004)(河北省高校人文社会科学重点研究基地(石家庄铁道大学) 河北 石家庄 05004)(燕山大学信息科学与工程学院 河北 秦皇岛 066004)

0 引 言

智慧旅游是随着云计算、下一代通信、数据挖掘等技术发展起来的一种新型旅游形态。其以移动终端应用为核心，实现用户和互联网的实时交互，使旅行安排更加个性化，并且便捷、高效，从而具有很大的研究价值。手机等各种电子移动设备以及GPS定位系统的发展，使得人们出行的地理位置信息很容易获取[1-3]。一方面，出行者在外出过程中停留形成的空间点连接起来形成了具有时空信息的轨迹；另一方面，伴随社交媒体应用的流行普及，例如，微博、微信等应用，地理位置与文本数据的融合变得非常普遍。轨迹中蕴含的丰富语义信息，如道路状况、天气条件、邻近朋友等为智慧旅游中越来越多应用和研究提供了助力。例如，在旅游系统中，用户除了记录自己的位置信息以外，还包括感兴趣点类型、地理环境、用户评价、图片、视频等数据。通过将轨迹中的时空信息与文本数据融合可以得到带有语义标签的轨迹，被称为语义轨迹[5-6]。例如用户A在a点购物，在b点住宿，那么购物、住宿等活动就是与空间点相对应的语义信息。由于轨迹的数量是相当庞大的，如何有效地对海量轨迹进行查询，获取最能满足客户需求的轨迹具有重要的应用价值。

在轨迹数据上进行查询处理已有大量的研究工作[4-16]。然而，现有大部分工作仅考虑轨迹上的时空信息，忽略了轨迹上的语义信息。例如，某驴友希望从历史旅游轨迹线路中寻找满足一定要求的轨迹作参考。倘若只考虑地理位置的因素，则可以通过布尔查询[11]、skyline查询[14]或最近邻kNN[15]查询等得到合适的匹配路线。然而，现实中很多情况下用户不仅对地理位置有要求，同时对语义也有要求。如驴友期望在自己预设的地点附近进行餐饮、参观和购物等需求。以图1为例，用户想在q1点附近进行{a,c}两项活动，在q2点附近进行{e}活动。Tr1、Tr2、Tr3是系统中的原有的旅行轨迹，当用户向系统输入他想进行的活动及地点后，系统应返回包含用户所需要的全部活动{a,c,e}且从空间位置上距离查询点最近的k条轨迹，即语义轨迹的kNN查询。表1给出查询点到轨迹点的距离。

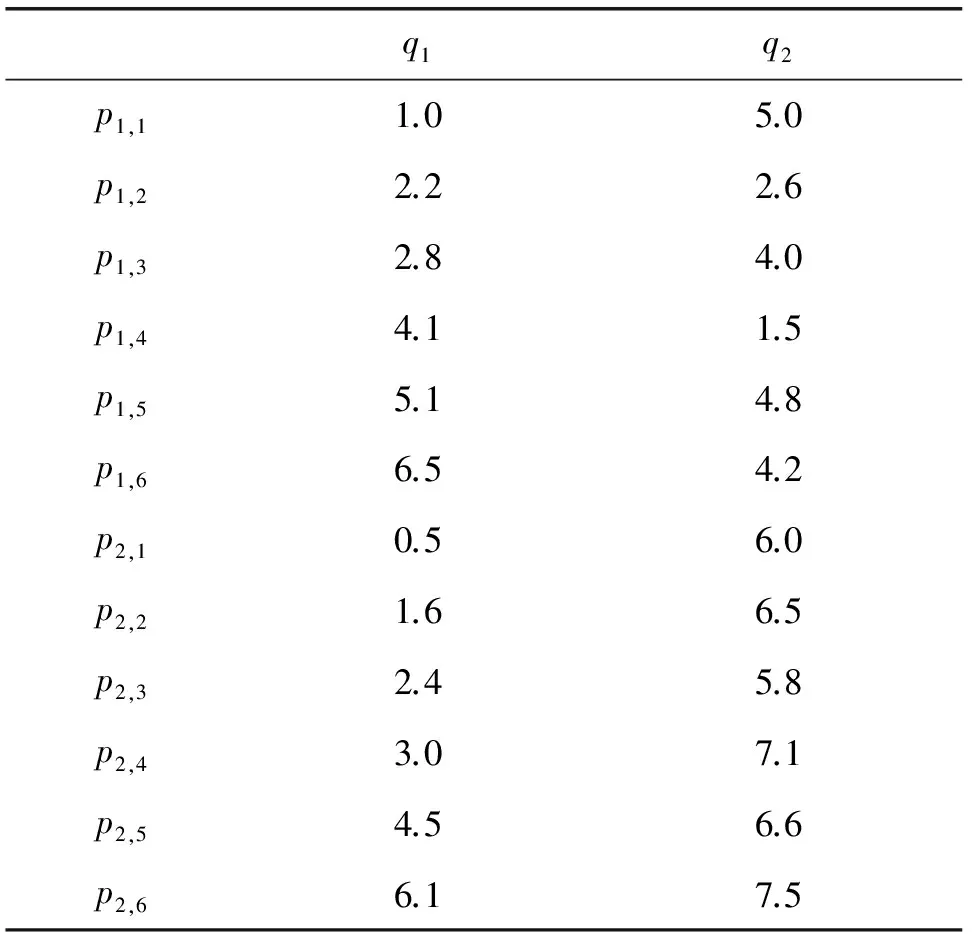
表1 示例中Tr1、Tr2轨迹点到查询点的距离

本文正是针对智慧旅游中语义轨迹上的k最近邻查询问题进行研究。基于R-tree融合位置上的文本信息提出了ITS-tree索引结构(包括IT-tree和S-树两个部分)，索引了原始轨迹特征点的空间信息和语义信息，可同时从空间和文本两个方面对轨迹进行剪枝。利用最小最佳优先原则，首先遍历IT-tree，从原始的语义轨迹中先获取候选轨迹集，然后对候选轨迹利用S-树进行轨迹结果的求精。

1 相关工作

现有在轨迹数据上的查询工作，按照查询点的个数的不同可分为两类：一类是单点查询，即查询满足用户当前位置和语义需求的轨迹数据；另一类是多点查询，即查询中包括的位置可以是一个点集合，语义可以是用于描述整条轨迹亦可以是描述每一个位置采样点的关键字集合。文献[11]给定用户查询位置和语义集合，返回包含用户语义并且匹配距离最短的k条轨迹。文献[6]提出的近似关键字查询 AKQST与传统空间语义查询不同，在查询集合中仅指定语义集合，但并没有涉及位置信息。该方法返回k条包含最相关语义且旅行代价最小的k条子轨迹。文献[7]中，每一条轨迹上带有一个文本关键字集合，提出了面向用户的轨迹查询UOTS。该方法返回距离查询点最近的轨迹，并且查询点的集合可以是有序序列，也可以是无序序列。文献[16]在位置空间、语义信息的基础上，增加了一个衡量标准即打分信息。在用户给定起点、终点以及语义信息下，该方法返回包含查询中所有语义信息、以及轨迹长度满足距离要求并且评分最高的轨迹段。文献[5]提出一种GAT新型网格索引结构，以层次的方式组织轨迹片段及其活动信息。利用best-first搜索框架，通过空间邻近和活动遏制同时修剪大量不合格的轨迹，有效地处理了空间文本查询。但由于为每一个语义构建一棵树，当需查询的语义较多时，会导致对HICL进行多次遍历，查询代价较高。

2 问题的形式化描述

方便起见，本文将游客在某地点上进行的活动，如住宿、餐饮、购物等，作为该位置的语义信息，其全集用A表示，小写字母表示语义实例。语义轨迹是一系列被赋予活动语义的点序列，用Tr表示，轨迹上的点用p来表示，即Tr={p1，p2，p3，…}，轨迹上的点p同时具有位置和语义两方面信息，形式化的表示为pi=(x,y,φ)，其中φ={x|x∈A}表示该点附着的语义信息。用户输入的查询点集用Q{q1，q2，q3，…}表示，其中每一个查询点亦是语义位置点。

定义1(点匹配[5]) 给定某一查询点q，若轨迹上点子集的语义组成的并集是查询点语义集的超集，即q.φ⊆∪pi∈Trpi.φ，则称该点集是查询点q到轨迹Tr的点匹配，用pm表示。

很明显，针对某一个查询，轨迹上的点匹配存在多个。

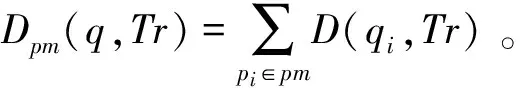
继续图1的例子，{p1,1,p1,2}、{p1,2,p1,3}、{p1,1,p1,2,p1,3}等都是查询点q1到轨迹Tr1的点匹配，其点匹配距离分别为3.2、5.0、6.0，最短点匹配距离为D(p1,1,q1)+D(p1,2,q1)=3.2。

本文的查询是点集合。因此，轨迹匹配距离定义与文献[5]相同。

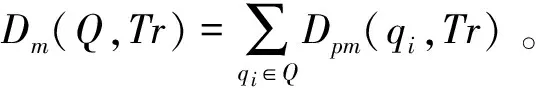
从定义3可以看出，轨迹匹配距离是所有查询点到该轨迹的任意一个点匹配距离的和。轨迹的最短匹配距离是所有匹配距离中的最小值。例如，针对Q={q1,q2}来说，轨迹Tr1的轨迹匹配距离为Dpm(q1,Tr1)+Dpm(q2,Tr1)。Tr1的最短轨迹匹配距离Dmm(Q,Tr1)为Dmpm(q1,Tr1) +Dmpm(q2,Tr1) =3.2+4.8=8.0。

本文的目标即从语义轨迹集合D中，根据查询点集合Q，寻找包含Q中所有关键字集合并且轨迹匹配距离最小的k条轨迹。具体来讲，查询结果需要满足空间与语义两方面要求：从语义的角度讲，查询结果中的点集合应包含所有查询点语义，示例中查询点语义集合是{a,c,e},则轨迹Tr2、Tr3不会出现在结果集中；从空间的角度讲，查询点到轨迹的轨迹匹配距离最短，以满足空间上轨迹兴趣点接近预设地点的要求。

3 ITS-树索引结构

为提高查询效率，本文提出了一个新的ITS-tree (即IT-tree+S-tree)索引结构。该索引结构分为两部分：(1) IT-tree，索引空间中的语义轨迹，融合了轨迹的空间信息、语义信息以及轨迹标识，便于查找候选轨迹集。(2) S-tree查找树，以语义词频为标准为轨迹标识号建立分段树，便于确定轨迹是否包含查询中的全部语义。

IT-tree：在R-tree的基础上融合了关键字到轨迹的倒排信息。为提高查找速率，在IT-tree中存储的是所有语义在整个数据库的词频，方便对语义进行比较和剪枝。在轨迹的所有点上建立R-tree，在叶子结点上建立词频到轨迹标识的倒排表，在中间结点上存储词频区间。具体来讲，叶子结点中的倒排表以该区域内覆盖的位置点所带的语义词频为关键字，指向一个轨迹标识列表，该列表中存储的是包含该语义信息的轨迹标识。中间结点存储该结点覆盖语义的降序词频区间，区间个数可由内存大小决定[5]。进行查询时，通过判断查询语义的词频区间与结点词频区间的是否存在交集，对IT-tree的结点进行剪枝(详见4.1节方法1)。表2是图1中的轨迹所带语义对应的词频，图2是这3条轨迹构建的IT-tree，图3是图2的树型结构示意图，图4示例了叶子结点N5中存储的倒排表。

表2 词频映射表

图2 IT-tree构建示例

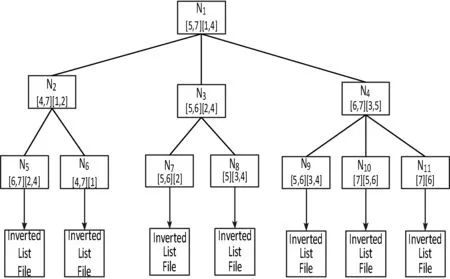
图3 IT-tree示意图

图4 叶子结点N5存储的倒排表

S-tree：在IT-tree上进行查询时，得到的是候选轨迹集。为进一步判断候选轨迹是否包含查询所需要的全部语义，需要对候选轨迹进一步求精，这正是S-tree的作用。S-tree的创建方法如下：通过从高到低排列的语义词频将连续的轨迹id划分为若干不相交的区间段，各区间所携带的语义信息用bitmap表来表示。这里假设轨迹id均是数字类型，如果轨迹id不是数字类型可以先将其数字化。具体划分方法如下：首先以是否包含最高语义词频为标准将轨迹id分为若干区间。例如，假设轨迹集包含10条轨迹，轨迹标识号为1～10，a为词频最高的语义，若Tr1-Tr3、Tr7-Tr10包含语义a，Tr4-Tr6不含语义a，则通过是否包含语义a可将轨迹标识号划分为[1,3], [4,6], [7,10]三个区间。接着使用词频次高的语义进行划分，与上述过程类似，若次高语义词频为b,则用b在由a划分好的区间的基础上再次进行划分，可得含a、b，含a但不含b，不含a但含b以及不含a、b的多个轨迹段。区间划分时，当语义词频总和达到90%时，划分停止。为每个划分好的区间建立bitmap表，按区间划分时语义由高到低的次序，每一位置1表示该位代表的语义存在，置0表示该位代表的语义存在，由bitmap表可知轨迹中包含的语义，如图5所示。所划分轨迹区间作为输入，根据线段树建立的方法，建成平衡的二分线段树，即S-tree。当从IT-tree中得到候选轨迹集后，以候选轨迹标识作为关键字搜索S-tree，锁定轨迹id所在叶子结点区间。通过查看该区间的bitmap表，可知该轨迹是否包含全部词频在90%以内查询语义。若查询中包含词频小于10%的关键字，则在计算最短轨迹匹配距离之前查看轨迹活动列表结构，若所有词频小于10%的语义均有对应点，则进行下一步计算[5]。若候选轨迹包含所有查询语义则进一步计算查询点到候选轨迹的最短轨迹匹配距离。详见4.1节方法2。

图5 S-tree示例

4 k最近邻查询方法

方法遍历ITS-tree获取候选结果集，并计算候选结果集中轨迹的最短轨迹匹配距离。为防止出现查询结果遗漏，进一步对可能符合要求的轨迹进行验证，最终返回含有k条轨迹的结果集。

4.1 遍历ITS-tree获取候选轨迹集

方法利用best-first思想，首先在IT-tree上进行遍历获取满足到某一个查询点空间位置较近的k条轨迹。具体遍历方法如下：遍历过程维护队列seq，seq中的元素以结点到各查询点距离的最小值为排序关键字进行升序排序。首先将IT-tree的根结点放入队列seq。当seq不为空时，取出队头。判断是否存在查询点的语义关键字对应的词频落入该结点的语义区间中，如果没有则将这个结点及其分支过滤，否则，计算其孩子结点到各查询点的空间最短距离，将其孩子结点按最短距离升序插入队列中。当队头中取出的是叶子结点时，取出具体轨迹放入轨迹集中。持续进行遍历，直至轨迹集中包含k条轨迹，具体见方法1。

接下来，利用S-tree检查这k条轨迹是否满足查询语义的要求。针对每一条候选轨迹，若其包含查询要求的所有语义则进一步计算最短匹配距离。具体来讲，针对每一条候选轨迹，根据该轨迹的标识存在的叶子结点bitmap表，根据查询Q中的每一个查询语义在bitmap中对应位置是否为1判断该轨迹是否包含该语义。若发现轨迹未包含全部查询语义，则将该轨迹从轨迹集中删去。当然，该方法无法判断轨迹是否包含词频小于10%的查询语义，可以遍历轨迹活动列表，通过轨迹中是否有词频小于10%语义的对应点进行进一步判断。然而，由于这些语义出现的概率较低，并不影响查询方法的性能。对于满足语义要求的轨迹计算最短轨迹匹配距离[5]，并插入候选结果集。

方法1遍历IT-tree

1 输入：IT-tree，seq

2 输出：轨迹集

3 维护队列seq存储结点编号以及结点到查询点距离

4 When 遍历IT-tree

5 Node N=seq.pop()

6 检查是否有查询语义词频落在结点N的词频区间

7 if Y，计算孩子结点到当前查询点距mD(cni,q)

8 将cni按当前查询点距离的升序插入seq

9 else 删除N

10 if (cn==null)

11 取出轨迹Tri

12 if (Tri未经过求精)

13 将Tri插入轨迹集

14 if (轨迹集轨迹数+候选集轨迹数=k)

15 return 轨迹集

若候选结果集中轨迹数i

方法2轨迹求精结果

1 输入：轨迹集Q，k

2 输出：top-k Tr

3 用方法1遍历IT-Tree

4 When 取得轨迹集TR

5 if (所查询语义均在90%词频范围内)

6 遍历TR中Tri的S-tree查看该轨迹是否包含全部查询语义

7 else 遍历TR中Tri的S-tree和APL结构确定轨迹包含全部查询语义

8 if(Tri包含全部查询语义)

9 计算该轨迹最短匹配距离Dmm(Q，Tri)

10 将Tri插入候选结果集CRS，删除TR中的Tri

11 else 删除Tri

12 if (CRS轨迹数i

13 得到候选结果集CRS

14 验证并更新CRS，得到RS

15 return RS

4.2 候选轨迹求精及得到top-k轨迹

在4.1节中仅获得的是距离某一个查询点较近轨迹，包含距离一个查询点最近邻的轨迹不一定是距离所有查询点的距离和最小的轨迹。因此，仅经过4.1节方法计算获得的结果并不能覆盖全部解。为确保没有遗漏可行解，本节对当前未出现在候选结果集，但可能成为查询结果的轨迹进行进一步求证。具体方法如下：以每个查询点为圆心，以当前候选结果集中最大的轨迹匹配距离为半径，在IT-tree上执行范围查询，查询获得的结果且未在现有候选结果集中出现的轨迹即是被遗漏的可行解。该可行解进行验证，其验证方法是：计算该轨迹与查询的最短匹配距离，若该距离小于当前结果集中最大值，则将其依升序插入当前结果集，并删去结果集中最后一条轨迹。重复这个过程直至最终得到含有top-k条轨迹的结果集。

5 示例分析

图2为上文中的实例，设置k值为2，原始轨迹集中有Tr1,Tr2,Tr3三条轨迹，有2个查询点q1，q2，查询语义是{a,c,e}，其中q1查询语义为{a,c}，q2查询语义为{e}。建立图3所示IT-tree。

计算出的IT-tree中各结点到查询点的最短距离如表3所示。

表3 计算得各结点到查询点的最短距离

查询语义为{a,c,e}，其中c语义为语义词频小于10%的语义。首先将N1压入队列中，随后取出队列中第一个结点N1，所有查询语义均在N1内，得到其三个子结点N2,N3,N4。计算其子结点到查询点的距离插入队列中，再取头结点N2，由于{a,c}语义词频落入N2词频区间内，取N2孩子结点计算距离后插入队列中。取队头结点N5，得到轨迹Tr1，Tr2插入候选轨迹集。此时候选轨迹数i=k,返回对轨迹进行求精。

遍历S-tree至叶子结点可得Tr1的Bitmap表11111，包含语义{a,e}和Tr2的Bitmap表11110，不包含语义e，因此将Tr2删除。用文献[5]中计算Tr1的最短轨迹匹配距离，参照表1可知最短轨迹匹配距离为1.0+2.2+1.5+4.8=9.5，将Tr1插入结果集中。此时结果集中轨迹数为1，小于k，返回遍历IT-tree。

取队头结点N3，语义{a,c,e}的词频落入的N3的词频区间，计算孩子结点N7、N8到各查询点的距离插入队列中。接着取队头结点N6，语义a的词频落入N6词频区间中，取出轨迹Tr1、Tr2，由于已经过遍历，不对候选结果集进行更新。接下来取队头N7，语义c的词频落入N7的词频区间，取出轨迹Tr1，不对轨迹集进行更新。取队头N4，语义{a,e}落入其词频区间，取N4的孩子结点，计算距离插入队列中。如此进行下去，可在 取到轨迹Tr3，返回Tr3进行验证，在S-tree叶子结点中3所在区间可得Bitmap表11111，由轨迹活动列表不含c，将其删除。由于遍历结束，候选结果集中仅有Tr1。

检验：以q1、q2为圆心，当前结果集中轨迹Tr1的最短匹配距离8.0为半径进行范围查询，检验从查询范围内覆盖的叶子结点中取得的轨迹是否有未出现在结果集中的情况。重复求精过程，对结果集进行更新。由于本例中轨迹数量较少，因此仅有{Tr1}满足要求。

本例中只针对每个查询点对IT-tree进行一次遍历。若使用文献[5]工作提供的方法，则要分别针对语义a、c、e对索引结构进行多次遍历，查询代价较高。

时间代价分析：查询方法主要分为两个部分：第一部分是利用IT-tree和S-tree索引结构找出候选结果集。假设查询点个数为|q|，n为轨迹数据集中点的个数，|D|为语义的值域中值的个数，算法的时间复杂度为O(|q||D|n2)。第二部分为根据候选结果集求解精确匹配距离，在该部分中，我们利用文献[1]的匹配算法，所以时间代价与文献[1]一致。

本文提出的方法可以进一步从下面两个问题进行提高与改进。一是IT-tree是基于轨迹中的离散点来构建的，从IT-tree中得到候选轨迹存在重复计算的情况。此点增加轨迹访问数组visit[]解决。二是虽然S-tree索引结构是基于语义词频占总词频的前90%的语义构建，但S-tree的高度依然是语义信息集合的值域|D|，当语义很多时，S-tree可能过高。此点可利用语义信息的词频分布降低S-tree索引结构的树高，对查询算法的效率做进一步优化提升。

6 结 语

本文针对旅游系统中的kNN语义轨迹查询问题,介绍了相关背景及工作，提出ITS-tree索引以期通过改进索引结构和方法提高查询的效率。IT-tree在R-tree索引空间信息的基础上存储区域点的语义信息，并通过叶子结点中的倒排表获取候选轨迹；用S-tree结构来检查轨迹是否满足语义要求，提高了语义检查的精确性。在进行查询时通过同时考虑查询点的所有语义，减少查找次数；使用查询语义词频与中间结点词频区间是否存在交集，对IT-tree结点进行剪枝，提高查找效率。接下来的工作将进一步对索引及方法进行优化，验证方法的有效性。

[1] 刘晓乐,李博. 隐私保护下的组最近邻查询算法研究[J]. 计算机应用与软件,2016,33(5):302- 306.

[2] 林娜,郑亚男. 基于出租车轨迹数据的路径规划方法[J]. 计算机应用与软件,2016,33(1):68- 72.

[3] 肖艳丽,张振宇,杨文忠. 基于GPS轨迹的用户移动行为挖掘算法[J]. 计算机应用与软件,2015,32(11):83- 87.

[4] 李万高. 路网中基于最短路径的最近邻查询算法研究[J]. 计算机应用与软件,2014,31(7):59- 61,68.

[5] Zheng K, Shang S, Yuan N J, et al. Towards efficient search for activity trajectories[C]//IEEE International Conference on Data Engineering. IEEE Computer Society, 2013:230- 241.

[6] Zheng B, Yuan N J, Zheng K, et al. Approximate keyword search in semantic trajectory database[C]//IEEE, International Conference on Data Engineering. IEEE, 2015:975- 986.

[7] Shang S, Ding R, Yuan B, et al. User oriented trajectory search for trip recommendation[C]//Proceedings of the 15th International Conference on Extending Database Technology—EDBT ’12. 2012:156- 167.

[8] 李晨, 申德荣, 朱命冬,等. 一种对时空信息的kNN查询处理方法[J]. 软件学报, 2016, 27(9):2278- 2289.

[9] 丁治明. 一种适合于频繁位置更新的网络受限移动对象轨迹索引[J]. 计算机学报, 2012, 35(7):1448- 1461.

[10] 宋晓宇, 许鸿斐, 孙焕良,等. 基于签到数据的短时间体验式路线搜索[J]. 计算机学报, 2013, 36(8):1693- 1703.

[11] Gao C, Lu H, Ooi B C, et al. Efficient Spatial Keyword Search in Trajectory Databases[DB]. eprint arXiv:1205.2880, 2012.

[12] Chen Y, Jiang K, Zheng Y, et al. Trajectory simplification method for location-based social networking services[C]//International Workshop on Location Based Social Networks, Lbsn 2009, November 3, 2009, Seattle, Washington, Usa, Proceedings. DBLP, 2009:33- 40.

[13] 赵苗苗. 基于出租车轨迹数据挖掘的推荐模型研究[D].北京:首都经济贸易大学, 2015.

[14] Aljubayrin S, He Z, Zhang R. Skyline Trips of Multiple POIs Categories[C]//International Conference on Database Systems for Advanced Applications. Springer International Publishing, 2015:189- 206.

[15] Zheng B, Zheng K, Xiao X, et al. Keyword-aware continuous kNN query on road networks[C]//IEEE, International Conference on Data Engineering. IEEE, 2016:871- 882.

[16] Chen W, Zhao L, Xu J J, et al. Trip Oriented Search on Activity Trajectory[J]. Journal of Computer Science & Technology, 2015, 30(4):745- 761.