汽车变速器动态性能研究
2018-07-04贾贵川
□贾贵川 □王 刚 □章 超
长安大学 汽车学院 西安 710064
汽车变速器是汽车传动系统的重要组成部分,直接影响汽车的平顺性、稳定性。变速器的使用寿命与工作过程中的稳定性是评价整车性能的指标。变速器在齿轮啮合过程中会产生动态啮合力,啮合力的大小对变速器的正常工作有显著影响,因此有必要对齿轮啮合力进行研究[1]。笔者通过CATIA三维绘图软件建模,随后对变速器进行动力学仿真分析,得出各级齿轮传动过程中的啮合力、啮合频率,反映变速器在正常工作过程中的某些特性,可以为变速器的设计、齿轮与轴的校核提供便利,并且对后期的优化设计与噪声控制具有指导意义。
1 变速器传动机构
笔者以某轻型货车为研究对象,货车采用的变速器为5+1挡的中间轴式变速器,即具有五个前进挡与一个倒退挡。具有中间轴的三轴变速器中,第一轴的前端经轴承支承在发动机飞轮上,第一轴的花键用来装设离合器的从动盘;第二轴的前端经轴承支承在第一轴后端的孔内,经啮合套连接后可得到直接挡;第二轴的末端经花键与万向节连接,可以将动力经传动系统传递给后轮驱动桥[2]。发动机的动力由离合器传递到变速器的第一轴,再经中间轴传递到第二轴输出。轴上的齿轮为常啮合齿轮,换挡时拨叉作用于同步器进行换挡。变速器在动力传递过程中起到变速增扭的作用,进而满足车辆在各个工况下的行驶要求[3]。
变速器的传动机构如图1所示。图1中Z1为第一轴常啮合齿轮,Z2为第二轴五挡齿轮,Z3为第二轴三挡齿轮,Z4为第二轴二挡齿轮,Z5为第二轴一挡齿轮,Z6为倒挡齿轮,Z7为中间轴常啮合齿轮,Z8为中间轴五挡齿轮,Z9为中间轴三挡齿轮,Z10为中间轴二挡齿轮,Z11为中间轴一挡齿轮,Z12为中间轴倒挡齿轮,Z13为倒挡轴倒挡齿轮。

图1 变速器传动机构
2 三维实体建模
选取前进挡一挡为研究对象,各齿轮参数见表1,齿轮按7级精度设计。
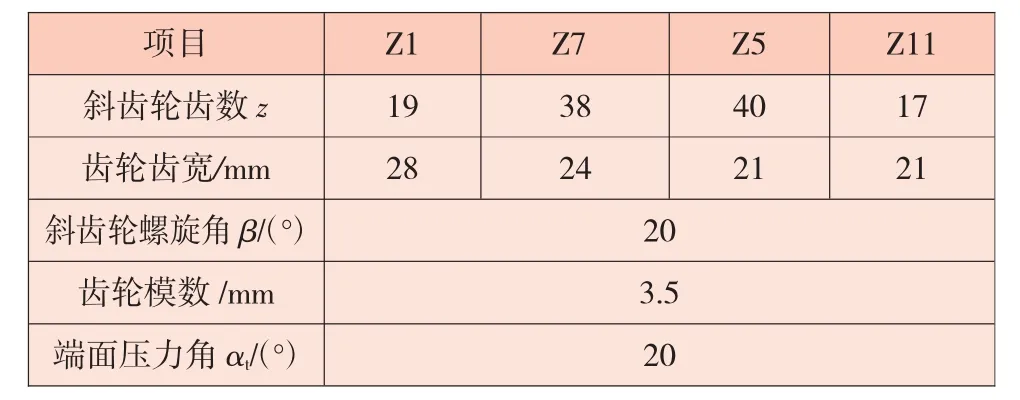
表1 前进挡一挡齿轮参数
由于ADAMS软件的三维建模能力不强,因此需要在CATIA中对变速器的零件进行装配,装配完成后需要对装配图进行干涉检查,防止因为模型的误差造成分析结果出错。根据表1中的参数在C ATIA中建立变速器前进挡一挡三维仿真模型,如图2所示。
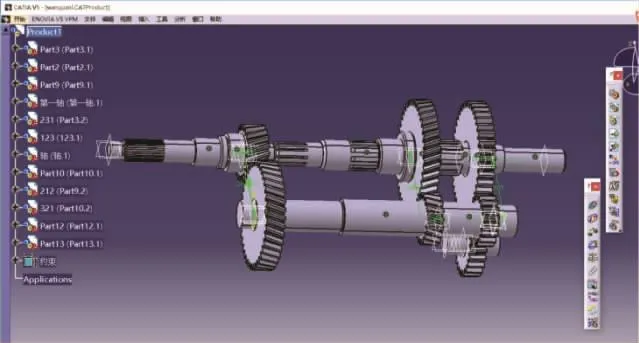
图2 变速器前进挡一挡三维仿真模型
3 虚拟仿真研究
3.1 ADAMS建模
将CATIA中的装配图转换为.stp格式。取前进挡一挡为研究对象导入ADAMS,在ADAMS中删去对分析结果影响不大的零部件,简化模型,同时减小仿真计算的工作量。变速器前进挡一挡ADAMS仿真模型如图3所示。定义材料属性均为钢材,密度为7.8×10-6kg/mm3,弹性模量为 207GPa,泊松比为 0.29。

图3 变速器前进挡一挡ADAMS仿真模型
3.2 定义约束
根据变速器传动机构定义约束类型,各构件的约束类型见表2。
3.3 定义接触
在齿轮传动过程中,轮齿间的相互碰撞啮合会产生接触力,因此需要定义每对齿轮的接触力,进而求得各个轮齿间的啮合力。在ADAMS的View模块中,计算接触力的方法有两种,一种是补偿法,一种是冲击函数法。冲击函数法根据冲击函数来计算两个构件之间的接触力。接触力由两个部分组成:一是由于两个构件之间相互切入而产生的弹性力,二是由相对速度产生的阻尼力[4]。笔者采用冲击函数法,令A为冲击函数,则有:

表2 构件约束类型
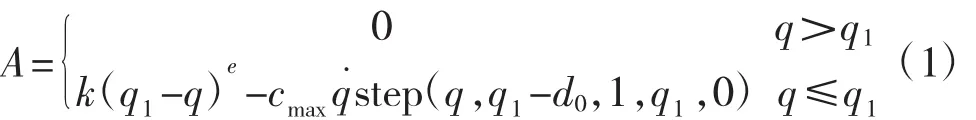
式中:q为两齿轮之间相互切入的深度;为速度;k为刚度系数;e为刚性指数;cmax为最大阻尼系数;d0为阻尼达到最大值时的切入量;q1为A的阈值。

式中:r为齿轮相对曲率半径;E0为相对弹性模量;u为两齿轮的齿数比;d1为较小齿轮的分度圆直径[5];αn为斜齿轮的端面啮合角;μ1、μ2为两齿轮的泊松比;E1、E2为两齿轮的弹性模量。
式(1)中 k(q1-q)e计算结果为弹性力,cmaxq˙step(q,q1-d0,1,q1,0)计算结果为阻尼力。
由式(2)~式(4)可得 Z1、Z7的刚度系数k1=1.05×106N/mm,Z5、Z11 的刚度系数 k2=2.7×105N/mm。金属材料的刚性指数e=2.2,阻尼系数c=40 N·s/m,阻尼最大时切入深度d0=0.07 mm,摩擦力类型选用库仑法。
3.4 添加驱动与负载
设发动机输入轴转速为1 800 r/min,变速器输出轴添加力矩为1 638 N·m的负载,为了防止在仿真过程中出现突变,在ADAMS中使用step函数来保证驱动添加的平稳性,step(time,0,0,0.2,10800D)表示在0.2s内使转速平稳加快到1800r/min,即10 800(°)/s,step(time,0,0,0.2,1638000) 表示使负载在0.2 s内平稳增大到1 638 N·m,其中time是时间变量,为0.5 s。仿真步长影响结果的精确性,且取决于计算机性能与模型的复杂程度,笔者将仿真步长设置为 3 000步[6]。
3.5 仿真结果与分析
Z1与Z7啮合力仿真结果如图4所示,Z5与Z11啮合力仿真结果如图5所示。
对齿轮啮合力的时域图进行快速傅里叶变换,可得到频域图。在ADAMS中,齿轮的轴向力沿X轴方向,径向力沿Y轴方向,圆周力沿Z轴方向。与X轴、Y轴、Z轴方向相同为正,反之为负。由时域图可以看出,仿真初始时刻啮合力出现一极大值,这是由启动时刻齿轮啮合冲击引起的,与实际情况相符。在0~0.3 s期间,变速器处于加速阶段,笔者仿真采用step函数使转速稳步加快,因此三个方向的啮合力也逐渐增大,0.3 s以后转速稳定,啮合力也不再加大,并稳定在某值处上下波动,波动的幅值具有周期性,这与在啮合过程中轮齿的啮入啮出相符。在齿轮传动中,齿轮所受的动载荷与齿轮加工精度、齿轮副重合度、轮齿受载变形等均有关。

图4 Z1与Z7啮合力仿真结果

图5 Z5与Z11啮合力仿真结果
为了与仿真作对比,笔者利用机械设计中的经典公式计算齿轮啮合力[7],其圆周力Ft为:

式中:T为转矩;d为齿轮分度圆直径。
径向力Fr为:

轴向力Fa为:

取仿真曲线中稳定阶段的啮合力与理论值相对比,具体见表3。
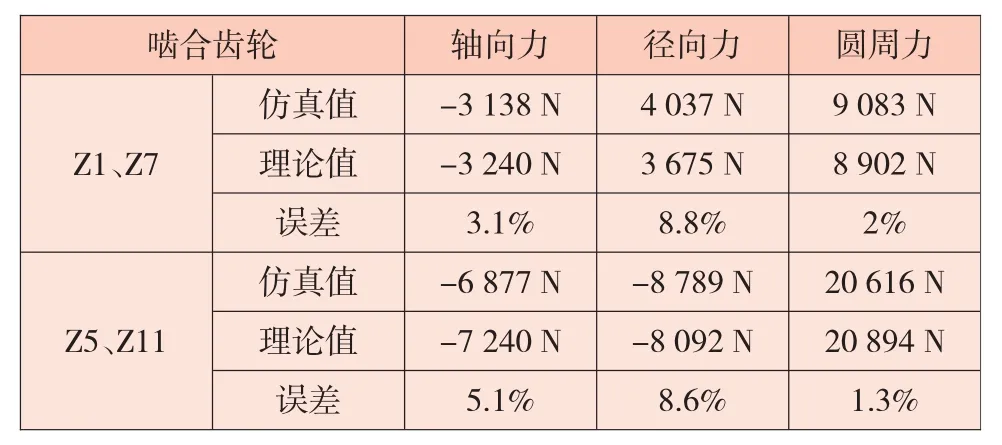
表3 仿真值与理论值对比
由表3可以看出,仿真值与理论值较为接近,误差在10%以内。
在频域内进行分析,得到齿轮的前三阶啮合频率,见表4。

表4 齿轮前三阶啮合频率Hz
Z1、Z7啮合频率的主频率为569 Hz,相应的啮合力幅值也最大,为124 N。Z5、Z11啮合频率的主频率为255 Hz,对应的啮合力幅值为105 N。齿轮啮合频率f计算式为[8]:

式中:n为齿轮轴转速。
变速器输入轴的转速为1 800 r/min,输出轴的转速为382 r/min。由此计算出Z1、Z7的啮合频率为570 Hz,Z5、Z11的啮合频率为255 Hz,与仿真结果很接近。啮合频率的整数倍处会出现峰值,峰值随频率的增大而逐步减小。通常可以通过对齿轮齿向与齿廊修形、提高齿轮的加工安装精度来减小齿轮啮合频率的幅值,进而降低变速箱的振动与噪声[9-10]。
3.6 不同加速时间对齿轮啮合力的影响
在不改变输入轴转速、输出轴转速、仿真时间、仿真步长的情况下,改变仿真加载时间,即输入轴的转速从0加快到1 800 r/min的时间改变为0.1 s、0.2 s,0.3 s,再次对仿真进行分析。以Z1与Z7的圆周力为例,进行三种加速时间的仿真,结果如图6所示,不同加速时间对应的齿轮啮合力见表5~表7。
由表5~表7可以看出,齿轮啮合力在平稳阶段与整个仿真阶段的最大值是相同的,且加速阶段的最大值与平稳阶段的最大值相差不大,说明齿轮啮合力是平稳增大的。加速时间为0.1 s时的整个仿真阶段啮合力最大值大于其它两个加速时间,加速时间为0.3 s时的啮合力平均值最小,且均值随加速时间的增加而减小。
4 总结
基于CATIA软件建立变速器的三维仿真模型,并且在ADAMS软件中建立仿真模型,实现了变速器前进挡一挡的动力学仿真,得到了两对齿轮的啮合力。仿真结果与理论计算值误差很小,说明模型建立较为合理,为变速器与其它齿轮传动系统的强度校核提供了帮助。
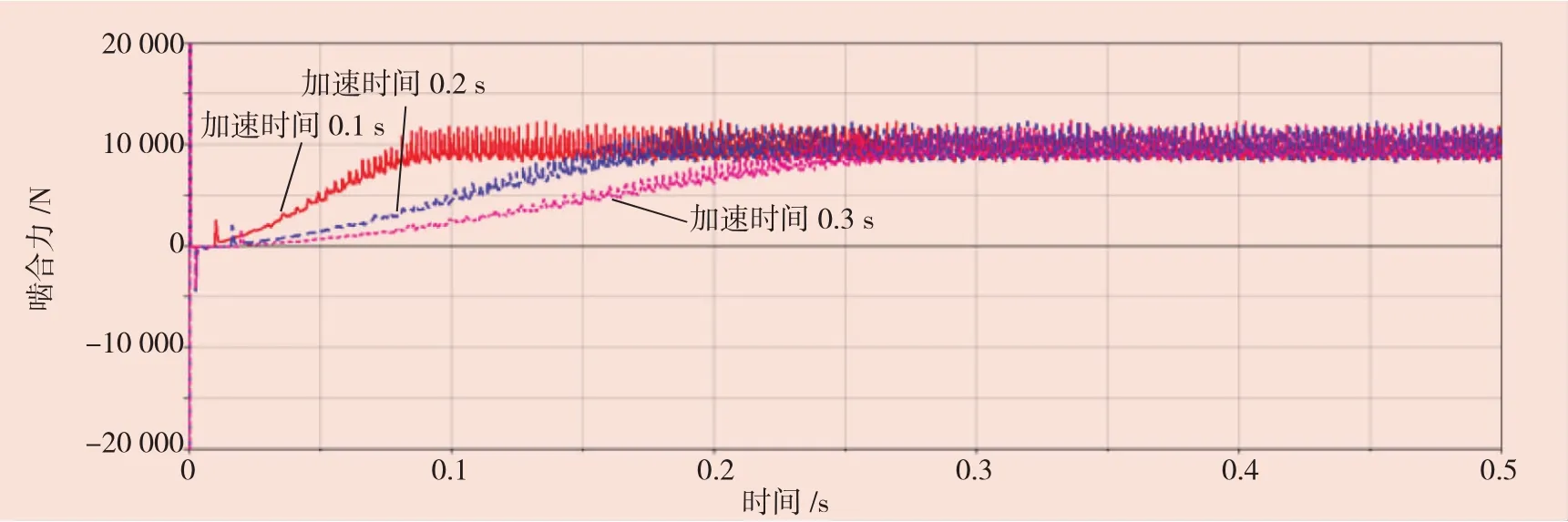
图6 齿轮啮合力时域图
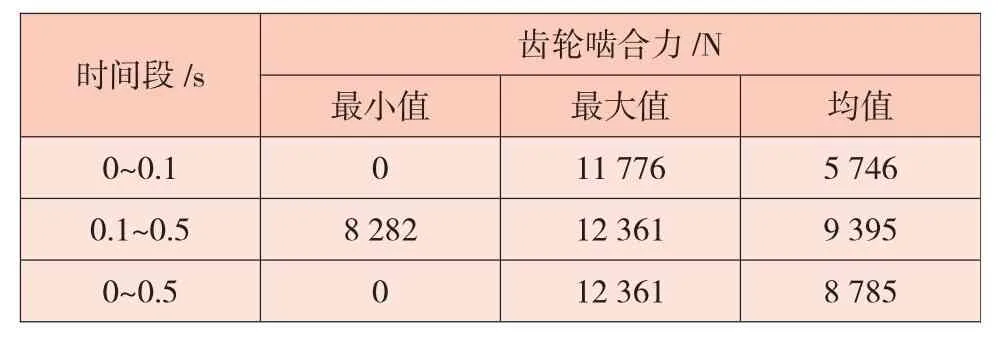
表5 加速时间0.1 s时齿轮啮合力

表6 加速时间0.2 s时齿轮啮合力

表7 加速时间0.3 s时齿轮啮合力
仿真得到了变速器前进挡一挡齿轮的啮合频率和与之对应的幅值,可以通过齿轮修形、提高齿轮加工精度与安装精度来减小啮合频率对应的幅值。同时,在设计箱体时,固有频率应尽可能远离啮合频率,以免引起共振,并且对降低变速箱的振动噪声具有参考意义。
改变齿轮的加速时间,由三种加速时间的仿真结果分析可知,齿轮的加速时间会影响齿轮啮合力的幅值,加速时间越短,齿轮啮合力的均值越大。因此,在仿真时应选取合适的加速时间。
[1]卫良保,韩斌,许黎明,等.基于ADAMS的叉车变速箱动态特性分析[J].机械传动,2017,41(6):154-158.
[2]王望予.汽车设计[M].4版.北京:机械工业出版社,2004.
[3]吉林大学汽车工程系.汽车构造[M].5版.北京:人民交通出版社,2006.
[4]李增刚.ADAMS入门详解与实例[M].2版.北京:国防工业出版社,2014.
[5]冯洋,李庆忠,裴罗特.基于ADAMS汽车前照灯调光电机的传动摩擦影响分析[J].机械传动,2015,39(9):161-163.
[6]熊倪,王匀,郭玉琴,等.基于ADAMS的动力钳齿轮传动系统动态载荷仿真分析[J].机械制造,2016,54(1):11-13.
[7]成大先.机械设计手册[M].5版.北京:化学工业出版社,2008.
[8]汪奇谋,李华,姚进.基于ADAMS的变速箱传动系统的动力学仿真[J].机械传动,2013,37(6):75-77.
[9]郭红珍.齿轮的噪声及减噪措施[J].机械管理开发,2009,24(1):16-17.
[10]罗小林,蒙鹏宇,钟武昌.汽车变速器的噪声源分析与降噪设计[J].机械制造,2016,54(1):34-36.
