邻域决策的随机约简与集成分类研究
2018-07-04余思成杨习贝陈向坚窦慧莉王平心
余思成,杨习贝,2,陈向坚,窦慧莉,王平心
1(江苏科技大学 计算机学院,江苏 镇江 212003)
2(南京理工大学 经济管理学院,南京 210094)
3(江苏科技大学 数理学院,江苏 镇江 212003)
1 引 言
为了使得粗糙集[1]方法能够处理连续型数据以及混合型数据,Hu等人提出了邻域粗糙集的概念[2,3].邻域粗糙集以其简单直观的建模手段且灵活的尺度表示方式,受到了众多学者的广泛关注,近年来相关领域研究取得了丰硕的成果[4-11].
在邻域粗糙集理论中,邻域决策错误率是一个重要的概念[12].所谓邻域决策错误率,实际上是借助留一验证的技术,描述邻域分类器在样本集中发生错误判断的程度.与传统粗糙集方法中基于近似质量、条件熵等约简形式[13-16]不同,邻域决策错误率为从分类学习的视角研究属性约简问题提供了一种度量标准.利用基于邻域决策错误率的属性约简,可以获得使得邻域决策错误率能够被降低的属性子集.然而利用启发式算法求解基于邻域决策错误率的约简,得到的仅仅是一个局部最优属性子集,考虑到样本集中可能存在多个满足邻域决策错误率降低这一约束条件的属性子集,因此可以借助集成的思想来研究邻域分类问题,其目的是期望充分利用多个约简所提供的信息,提升邻域分类器的性能.
集成学习的初衷是把若干个基分类器的分类结果通过一定的方法融合起来,从而取得比单个基分类器更好的性能[17-19].文献[20]的研究表明集成分类器取得良好效果的一个关键在于基分类器的差异性,因而如何获取具有较大差异的基分类器已然成为集成学习研究中的一个热点问题.传统的集成学习通常利用Bagging[21-23],Boosting[24-26]等调整样本的方法来获得有差异性的基分类器.此外亦可以从属性的角度出发,通过抽取不同的属性子集分别加以训练,其目的是获得基于不同属性空间下的一组基分类器[27].显然,后者与粗糙集理论中属性约简问题是有着密切关联的,若能充分利用多个不同约简所提供的信息,则将有助于在粗糙集理论中使用集成策略以提升学习性能.鉴于此,笔者首先设计了一种基于邻域决策错误率的随机属性约简算法,利用该算法可以从原始属性集中提取多个满足邻域决策错误率降低这一约束条件的属性子集,其次利用这些属性子集构造一组邻域分类器,最后通过对测试样本在这些分类器上给出的类标记投票得到最终的分类结果.由于随机约简方法[28]可以获取多个属性子集,因此包含了比单个属性子集更充分的信息,从而可以对邻域分类器的性能产生正面影响.
2 邻域分类器与邻域决策错误率
邻域粗糙集是Hu等人[2,3]提出的一种扩展粗糙集模型,它提升了粗糙集理论对于数值型数据的处理能力.邻域粗糙集的处理对象依然是一个决策系统DS=(U,AT∪D),其中U是所有样本构成的集合,称其为论域,AT是所有条件属性的集合,D是决策属性,U/IND(D)={X1,X2,…,Xn}表示根据决策属性D所诱导的论域上的划分.
定义1[2]. 称二元组
在决策系统中,借助邻域的概念,可以构造邻域分类器[3]如算法1所示:
算法1. 邻域分类器
输入:决策系统DS=(U,AT∪D),测试样本y,邻域半径σ.
输出:测试样本类标记L(y).
步骤1. ∀x∈U,计算δ(y,x);
步骤2. 计算δ(y);
步骤4.Xj=arg max{Pr(Xi,δ(y)):∀Xi∈U/IND(D)};
步骤5.L(y)=j,输出L(y).
在利用邻域分类器进行分类学习的基础上,Hu等人进一步提出了邻域决策错误率(NDER)的概念[12].其核心思想是利用留一验证得到邻域分类器在U中的分类错误率,这个分类错误率即是邻域决策错误率.
定义2. 给定一个决策系统DS=(U,AT∪D),其邻域决策错误率为:
(1)
其中L(x)为邻域分类器输出的类标记,D(x)是x的真实类标记.
由定义2可以看出,邻域决策错误率是样本集中邻域分类器发生错误判断的程度.
3 邻域决策错误率随机约简
利用邻域决策错误率,Hu等人给出了相应的属性约简描述[12].
定义3. 给定一个决策系统DS=(U,AT∪D),∀A⊆AT,A被称为一个邻域决策错误率约简(NDERR),当且仅当NDERA≤NDERAT,且对于任意B⊂A,都有NDERB>NDERAT.
大家都知道的,当年美国总统尼克松访华时用的那双筷子,现在值多少钱了?十万不止。但也不是所有的附加上的东西都值钱,一张宣纸,齐白石在上面涂了几笔,这张纸就值大钱了。同样一张宣纸,隔壁张三抹了几笔,这张纸就废了。同样是几笔,差距咋就这样大呢?在于附加值。附加值有正数,也有负数。
由上述定义可以看出,利用邻域决策错误率的概念定义约简,其目的是使邻域分类器对约简后的样本集发生错误判断的程度降低.
在粗糙集理论中,贪心算法是求解约简的典型方法,若将邻域决策错误率降低作为约简条件,则通过贪心策略也可以求得一个局部最优属性子集[12].然而实际数据中可能存在多个满足邻域决策错误率降低这一约束条件的属性子集.为了获取并尽可能利用这些属性子集所提供的信息,需要通过恰当的途径求解尽可能多的满足条件的属性子集.文献[27]提出了一种基于邻域随机约简的方法:该方法放宽了贪心策略每一步选择最佳属性的要求,而采用随机选取前F个最佳属性中的一个添加到约简中,多次执行算法可以得到多个满足约简约束条件并且有一定差异的属性子集.将邻域决策错误率约简与邻域随机约简的方法结合,可以设计一种基于邻域决策错误率的随机属性约简方法如算法2所示.
算法2. 基于邻域决策错误率的随机属性约简
输入:邻域决策系统DS=(U,AT∪D),邻域半径σ,随机参数F.
输出:一个邻域随机约简red.
步骤1.red=ø;
步骤2. 计算NDERAT
步骤3. 若AT-red=ø则转至步骤 8;
步骤4. ∀a∈AT-red,计算NDER[a]∪red,并按照NDER[a]∪red值从小到大排序记为a1,a2,…,an;
步骤5. 从a1,a2,…,an的前F个,即a1,a2,…,aF中随机选取一个记为ak;
步骤6.red=red∪{ak};
步骤7. 若NDERred>NDERAT则转至步骤3;
步骤8. 输出red.
基于邻域决策错误率的随机属性约简算法经过多次运行,即可得到多个满足邻域决策错误率降低这一约束条件并且有一定差异的属性子集.
4 邻域分类器集成
利用邻域决策错误率随机约简,可以得到多个有一定差异的属性子集,通过这些属性子集可以构造多个邻域分类器,对给定的新样本在不同的邻域分类器上可能得到不同的类别,通过投票的方式对这些邻域分类结果加以集成,得到最终的输出类别,从而达到利用不同属性子集进行分类的目的.图1给出了一种借助邻域决策错误率随机约简获得多个属性子集并利用邻域分类器进行集成分类的方法.

图1 NDER随机约简分类策略Fig.1 NDER based randomized reduction and neighborhood classification strategy
由图1可以看出,基于NDER随机约简的邻域分类方案能够在满足邻域决策错误率降低这一约束条件的多个属性子集上产生多个分类结果,并对所得的结果进行投票,有望获得比单个属性子集更高的分类性能.同时该方案可以采用并行计算的方法进行优化,从而降低时间消耗.
5 实验分析
为了验证基于NDER随机约简集成算法的有效性,选取了12组UCI数据进行实验分析.数据集基本信息如表1所示.
实验环境为PC机,双核1.10GHz CPU,8G内存,windows10 操作系统 ,matlab R2012a 实验平台.
在本组实验中,设置随机属性约简的随机参数F=3,求得邻域决策错误率降低的属性子集数量为40个,即用40个基分类器集成(采用邻域分类器),并使用Kappa统计量[28,29]描述分类结果的一致性,选取了十个不同的邻域半径参数值,分别是0.05,0.1,… ,0.5.图2给出了上述12个数据集在十折交叉验证下,原始数据下的分类精度,利用传统启发式算法求邻域决策错误率约简(NDERR)得到的分类精度、邻域决策的一致性度量,利用邻域决策错误率随机约简集成(ELNDERR)的分类精度、邻域决策的一致性度量.
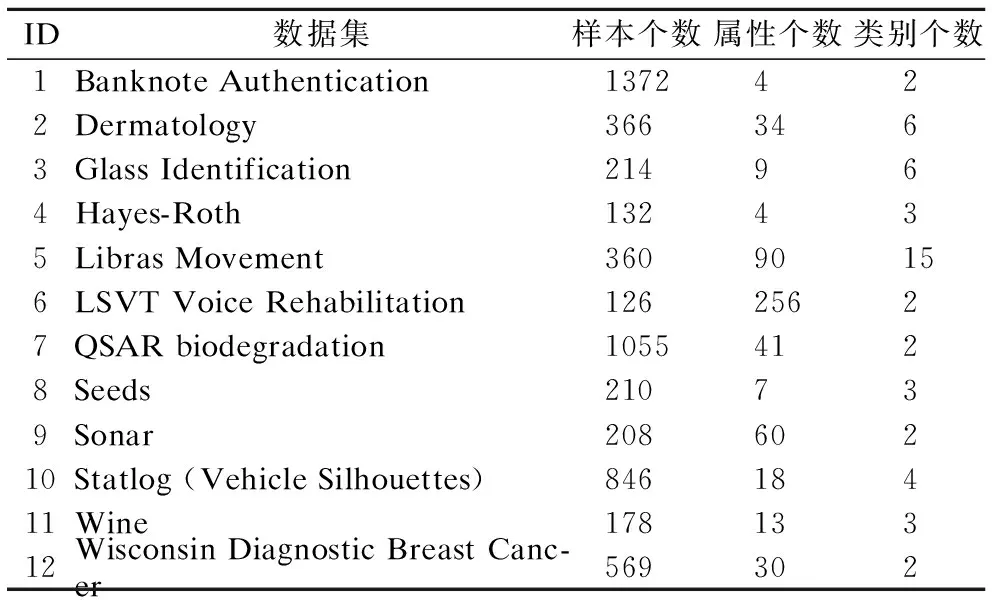
表1 数据集描述Table 1 Data sets description

图2 分类精度及一致性在不同约简下的对比Fig.2 Comparisons for classification accuracies and agreements among different reducts
从实验数据中可以看出,在绝大多数半径下,利用ELNDERR得到的分类结果,分类精度和分类结果的一致性都明显优于利用NDERR得到的结果,这表明ELNDERR方法从分类精度和鲁棒性两方面上对邻域分类器的性能有提升作用.此外,个别半径下约简后的邻域分类器分类精度低于原始属性的分类精度,例如,Seeds数据集在邻域半径参数0.25和0.3下原始属性的分类精度高于属性约简后的分类精度,又如Wine数据集在邻域半径参数0.15下原始属性的分类精度也高于属性约简后的分类精度,这主要是因为文中属性约简的目的是提高邻域决策的留一验证精度,而非十折交叉验证的精度.
6 结 论
邻域决策错误率约简,求取的是满足邻域决策错误率降低这一约束条件的属性子集,目的是通过降低邻域分类器的发生错误判断的程度提升邻域分类器的性能.通过构造基于邻域决策错误率的随机属性约简算法,利用求解得到的多个约简形成基分类器,对分类结果进行投票集成,旨在进一步提升邻域分类器性能.实验表明,在绝大多数半径下,基于邻域决策错误率随机约简的集成分类方法可以有效地提高邻域分类器的分类精度和分类鲁棒性.
在本文工作的基础上,笔者将就以下工作进行深入探讨:
1)提高约简效率,寻求更高效快速的求解算法;
2)利用邻域半径变化构造基分类器的集成策略;
3)基于随机属性约简的选择性集成方法.
:
[1] Pawlak Z.Rough set[J].International Journal of Computer & Information Sciences,1982,11(5):341-356.
[2] Hu Q,Yu D,Liu J,et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences,2008,178(18):3577-3594.
[3] Hu Q,Yu D,Xie Z.Neighborhood classifiers[J].Expert Systems with Applications,2008,34(2):866-876.
[4] Chen H,Li T,Cai Y,et al.Parallel attribute reduction in dominance-based neighborhood rough set[J].Information Sciences,2016,373:351-368.
[5] Lin Y,Li J,Lin P,et al.Feature selection via neighborhood multi-granulation fusion[J].Knowledge-Based Systems,2014,67(3):162-168.
[6] Liu Y,Huang W,Jiang Y,et al.Quick attribute reduct algorithm for neighborhood rough set model[J].Information Sciences,2014,271(7):65-81.
[7] Xu J,Xu T,Sun L,et al.An efficient gene selection technique based on fuzzy C-means and neighborhood rough set[J].Applied Mathematics & Information Sciences,2014,8(6):3101-3110.
[8] Yang X,Zhang M,Dou H,et al.Neighborhood systems-based rough sets in incomplete information system[J].Knowledge-Based Systems,2011,24(6):858-867.
[9] Bao Li-na,Ding Shi-fei,Xu Xin-zheng,et al.Extreme-learning machine algorithm based on neighborhood rough sets[J].Journal of University of Jinan,2015,29(5):367-371.
[10] Tang Chao-hui,Chen Yu-ming.Neighborhood system uncertainty measurement approaches.[J].Control & Decision,2014,29(4):691-695.
[11] Zhang Wei,Miao Duo-qian,Gao Can,et al.A neighborhood rough sets-based Co-training model for classification[J].Journal of Computer Research & Development,2014,51(8):1811-1820.
[12] Hu Q,Pedrycz W,Yu D,et al.Selecting discrete and continuous features based on neighborhood decision error minimization[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2010,40(1):137-150.
[13] Duan Jie,Hu Qing-hua,Zhang Ling-jun,et al.Feature selection for multi-label classification based on neighborhood rough sets[J].Journal of Computer Research & Development,2015,52(1):56-65.
[14] Liang Hai-long,Xie Jun,Xu Xing-ying,et al.New attribute reduction algorithm of neighborhood rough set based on distinguished object set[J].Journal of Computer Applications,2015,35(8):2366-2370.
[15] Jia H,Ding S,Ma H,et al.Spectral clustering with neighborhood attribute reduction based on information entropy[J].Journal of Computers,2014,9(6):1316-1324.
[16] Yang Xi-bei,Xu Su-ping,Qi Yong,et al.Rough data analysis method based on multi feature space[J].Journal of Jiangsu University of Science and Technology (Natural Science Edition),2016,30(4):370-373.
[17] Li Y,Si J,Zhou G,et al.FREL:a stable feature selection algorithm[J].IEEE Transactions on Neural Networks & Learning Systems,2014,26(7):1388-1402.
[18] Wang X,Xing H,Li Y,et al.A study on relationship between generalization abilities and fuzziness of base classifiers in ensemble learning[J].IEEE Transactions on Fuzzy Systems,2014,23(5):1638-1654.
[19] Sun Bo,Wang Jian-dong,Chen Hai-yan,et al.Diversity measures in ensemble learning[J].Control & Decision,2014,29(3):385-395.
[20] Zhou Z,Yu Y.Ensembling local learners through multimodal perturbation[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2005,35(4):725-735.
[22] Breiman L.Bagging predictors[J].Machine Learning,1996,24(2):123-140.
[23] Bi Kai,Wang Xiao-dan,Yao Xu,et al.Adaptively selective ensemble algorithm based on bagging and confusion matrix[J].Acta Electronica Sinica,2014,42(4):711-716.
[24] Korytkowski M,Rutkowski L,Scherer R.Fast image classification by boosting fuzzy classifiers[J].Information Sciences,2016,327:175-182.
[25] Schapire R E.The strength of weak learnability[J].Machine Learning,1990,5(2):28-33.
[26] Trzcinski T,Christoudias M,Lepetit V.Learning image descriptors with boosting[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2015,37(3):597-606.
[27] Valentini G,Masulli F.Ensembles of learning machines[M].Neural Nets,Springer Berlin Heidelberg,2002.
[28] Zhu Peng-fei,Hu Qing-hua,Yu Da-ren.Ensemble learning based on randomized attribute selection and neighborhood covering reduction[J].Acta Electronica Sinica,2012,40(2):273-279.
[29] Sim J,Wright C C.The Kappa statistic in reliability studies:use,interpretation,and sample size requirements[J].Physical Therapy,2005,85(3):257-268.
[30] Yang Chun,Yin Xu-cheng,Hao Hong-wei,et al.Classfier ensemble with diversity:effectiveness analysis and ensemble optimization[J].Acta Automatica Sinica,2014,40(4):660-674.
附中文参考文献:
[9] 鲍丽娜,丁世飞,许新征,等.基于邻域粗糙集的极速学习机算法[J].济南大学学报自然科学版,2015,29(5):367-371.
[10] 唐朝辉,陈玉明.邻域系统的不确定性度量方法[J].控制与决策,2014,29(4):691-695.
[11] 张 维,苗夺谦,高 灿,等.邻域粗糙协同分类模型[J].计算机研究与发展,2014,51(8):1811-1820.
[13] 段 洁,胡清华,张灵均,等.基于邻域粗糙集的多标记分类特征选择算法[J].计算机研究与发展,2015,52(1):56-65.
[14] 梁海龙,谢 珺,续欣莹,等.新的基于区分对象集的邻域粗糙集属性约简算法[J].计算机应用,2015,35(8):2366-2370.
[16] 杨习贝,徐苏平,戚 湧,等.基于多特征空间的粗糙数据分析方法[J].江苏科技大学学报(自然科学版),2016,30(4):370-373.
[19] 孙 博,王建东,陈海燕,等.集成学习中的多样性度量[J].控制与决策,2014,29(3):385-395.
[23] 毕 凯,王晓丹,姚 旭,等.一种基于Bagging和混淆矩阵的自适应选择性集成[J].电子学报,2014,42(4):711-716.
[28] 朱鹏飞,胡清华,于达仁.基于随机化属性选择和邻域覆盖约简的集成学习[J].电子学报,2012,40(2):273-279.
[30] 杨 春,殷绪成,郝红卫,等.基于差异性的分类器集成:有效性分析及优化集成[J].自动化学报,2014,40(4):660-674.
