TNT径高比对爆炸冲击波比冲量的影响研究

陈 铭，周云波，孙晓旺

(南京理工大学 机械工程学院， 南京 210094)

炸药在空气中爆炸时，会在非常短的时间内转变成大量高温高压的爆炸产物，爆炸产物强烈压缩空气，在空气中形成爆炸空气冲击波[1]，空气冲击波对其传播路径上的障碍物进行冲击，这是一个复杂大变形、强烈非线性的瞬态过程。军用车辆底部结构大多是壳、梁等基本构件组成的，当这些基本构件受到爆炸冲击时，会产生大的塑性变形甚至是断裂破坏而导致结构失去其原有的功能[2]。李金山[3]通过大量的数值计算与拟合，找到了炸药圆柱体的热爆炸临界参数与其长径比的关系，并指出长径比为5的有限长圆柱体可视为无限长圆柱体；谷鸿平等[4]研究了不同的起爆方式对柱形炸药空爆的影响，发现在5倍比值距离范围内，起爆方式可改变炸药爆炸冲击波场的局部分布形态；高轩能等[5]分析了炸药材料参数、TNT药量、单元网格密度、建模方式、空气域形状和炸药形状等参数变化对爆炸冲击波超压的影响，当比值距离小于2时，炸药材料参数、单元网格密度和炸药形状对数值计算结果的影响较大。爆炸空气冲击波对目标的作用与它作用在结构上的比冲量直接相关，本文在保证其他影响因素一致的基础上，具体研究TNT形状对结构响应的影响，评价爆炸冲击波的比冲量，对指导军用车辆结构优化有重要意义。

1 空中爆炸理论分析

1.1 爆炸产物的膨胀及压缩

炸药在空气中爆炸时，瞬间转变成高温高压的爆炸产物。爆炸产物在空气中进行膨胀，其结果是在爆炸产物内形成稀疏波[1]。

同时，爆炸产物强烈压缩空气，在空气中形成爆炸空气冲击波。爆炸产物的膨胀规律，可近似地用多次方指数型状态方程来表示

(1)

当爆炸产物膨胀到与周围未扰动空气的初始压力平衡时，其相应的体积为爆炸产物的极限体积，所对应的半径为极限体积半径[13]。对于圆柱形炸药，极限体积半径约为自身直径的30倍。但此时爆炸产物的膨胀并没有停止，而是由于惯性效应继续膨胀，直到惯性效应消失为止。此时，爆炸产物的压力又低于空气的初始压力，空气反过来对爆炸产物进行压缩，使其压力不断回升。同样由于惯性效应产物又被过度压缩，使爆炸产物的压力大于周围空气的压力，并开始第二次膨胀与压缩的过程。实验结果表明，对爆炸破坏作用有实际意义的只是第一次的膨胀与压缩过程。

1.2 爆炸冲击波的形成及传播

一般认为，当爆炸产物停止膨胀时，空气冲击波就与爆炸产物分离，并独自向前传播。爆炸冲击波在传播过程中，波的前沿以超声速传播，而正压区的尾部是以与空气初始压力相对应的声速传播，所以正压区被不断拉宽，受压缩的空气量不断增加，使得单位质量空气的平均能量不断降低。此外，冲击波的传播过程是不等熵存在因空气冲击绝热压缩产生的不可逆的能量损失。冲击波强度越大，这种不可逆的能量损失越大。因此，空气冲击波传播过程中波阵面压力在初始阶段衰减快，后期衰减平缓，传播到一定距离后，冲击波衰减为音波。爆炸空气冲击波的传播规律如图1所示。

1.3 空气冲击波对目标的作用

空气冲击波在遇到障碍物，如建筑物、军事设施时，会使其产生剧烈的变形。王芳等人通过研究在爆炸冲击波作用下四边约束方形靶板，不考虑弯曲效应，仅考虑膜力效应[11]，由能量守恒得到冲量加载区中比冲量作用下矩形板挠度的半经验公式[2]，如下：

(2)

当τ→0时，可以认为sinτ≈τ，又因为比冲量i=P·τ，所以上式可以简化为

(3)

式中，w0板的中心挠度，a、b、h分别为板的长、宽和厚度，i为比冲量，ρ为板的密度。

2 有限元模型的建立

王芳等人为研究爆炸冲击波下靶板塑性大变形响应做了五组在不同当量下，对不同厚度的靶板进行爆炸冲击波毁伤试验，炸药的高径比为1∶1，靶板为边长500 mm的正方形A3钢板，使用专用靶架，利用四周螺钉及压板将靶板的四边加紧。试验布置如图2所示。本文选择了其中的2组试验进行有限元建模以及对标，相应的试验数据如表1所示。

表1 试验数据

2.1 网格划分

为了确保仿真的准确性，有限元仿真模型采用与实验相同的布置形式，如图2所示。同时，考虑到布置的对称性以及节约计算成本，建立1/4仿真模型，单位制采用t-mm-s。

模型中空气网格为六面体单元，采用Solid ALE单点积分单元，非对称面采用无反射边界以模拟无限空气域。靶板网格与空气网格以交叉、重叠的方式实现结构网格与流体网格的耦合[7]。目标靶板尺寸为500 mm × 500 mm× 1mm，采用单元尺寸为10 mm的壳单元，单元总数为625。空气域采用圆柱形空气域结构，空气域包围目标靶版，网格大小为20 mm。炸药距离靶板中心980 mm，质量为700 g。如图3所示，利用ALE方法建立有限元模型，利用关键字*INITIAL_VOLUME_FRECTION_GEOMETRY来定义炸药的形状以及尺寸，此种方式无需建立炸药网格，用坐标值定义炸药爆炸位置[9]，起爆方式均为中心起爆。

2.2 材料模型

靶板采用*MAT_PIECEWISE_LINEAR

_PLASTICITY弹—塑性材料模型；炸药采用*MAT_HIGH_EXPLOSIVE_BURN高速燃烧材料模型和*EOS_JWL状态方程来描述压力、体积和内能之间的关系：

(4)

式中：P为压力；V为相对体积；E为初始内能密度；A、B、R1、R2、ω为材料常数。

空气单元采用*MAT_NULL空材料模型配合*EOS_LINEAR_POLYNOMIAL线性状态方程来描述

p=C0+C1m+C2m2+C3m3+

(C4+C5m+C6m2)E

(5)

式中：p为压力；m为相对体积；E为单位体积内能。

表2 靶板的材料参数

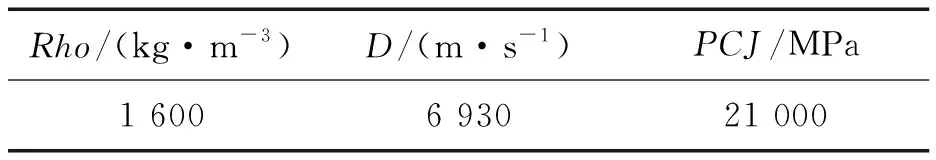
表3 炸药的材料参数

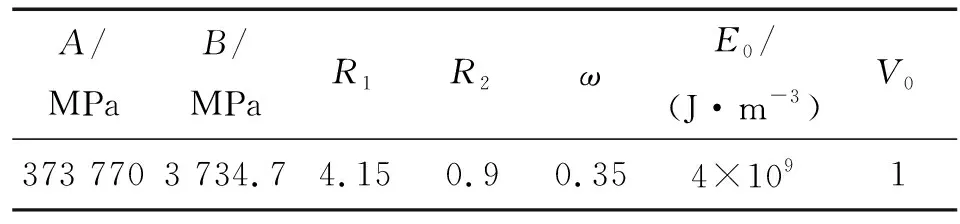
表4 炸药的JWL状态方程参数

表5 空气的材料参数

2.3 边界条件

在建立几何模型和进行有限元网格划分时，空气与靶板的网格可以重叠在一起，空气单元与靶板单元之间通过流固耦合定义彼此之间的连接，以实现力的传递。定义空气为EULERIAN流体域，目标靶板为LAGRANGIAN固体模型，采用*CONSTRAINED_LAGRANGIAN_IN_SOLID定义LAGRANGIAN目标靶板与EULERIAN空气域的流固耦合。靶板四边全约束。

3 仿真计算结果与试验结果分析

3.1 爆炸冲击波流场分析

图4为不同时刻爆炸冲击波的流场分布图。图4截取了700 g TNT的爆炸过程，爆炸中冲击波向四周扩散，

从图4可以看出，冲击波的波阵面接近于理想的球形爆炸冲击波。在爆炸后0.2 ms与靶板接触并耦合；0.5 ms之后冲击波流场基本覆盖整个空气域，此时靶板已经在强冲击作用下产生了较大的塑形变形，并且变形已经趋于稳定。

3.2 仿真计算分析

1) 起爆方式的影响

对比试验中采用的是后端单一起爆方式，而在军用车辆抗爆炸试验中，一般采用接近中心的单一起爆方式。两种起爆方式下靶板的中心挠度如表6所示，相对误差小于5%，满足工程要求，因此可以在此仿真模型采用中心起爆的方式代替后端起爆方式。

表6 两种起爆方式的中心挠度

2) 边界简化的影响

考虑到布置的对称性以及节约计算成本，仿真中建立1/4简化模型，并将其与全尺寸模型进行对比。由表7可见，1/4简化对称模型与全尺寸模型下靶板的变形量基本一致，对爆炸冲击波计算的影响较小。

表7 两种边界简化的变形量

3) 靶板中心挠度分析

爆炸冲击下约束方形板的响应分析如图5所示。将约束方形靶板中心挠度的仿真计算结果与试验结果进行比较。如图5(a)所示，在序号1的工况下，约束方形靶板在爆炸冲击波作用下应力达到390 MPa(超过了其235 MPa的屈服极限)，靶板中心位置出现的最大变形为82.2 mm。如图5(b)所示，在序号2的工况下，约束方形靶板在爆炸冲击波作用下应力达到368.8 MPa(超过了其235 MPa的屈服极限)，靶板中心位置出现的最大变形为76.2 mm，如表8所示。在不同板厚、装药当量和炸距的边界条件下，该算法以及数值计算模型所获得的中心挠度相对误差满足工程要求。

表8 中心挠度仿真计算结果与试验结果

4 圆柱炸药径高比的影响

在验证算法以及数值仿真计算的准确性后，在不改变圆柱炸药当量(700 g)的前提下，改变炸药的径高比，分析其变化对靶板变形的影响。定义h为高，D为直径，Q为圆柱形炸药的径高比

Q=D/H

(6)

考虑军用车辆爆炸试验中炸药形状的通用性以及炸药自身的稳定性，选取不同的径高比，如表9所示。

表9 圆柱炸药径高比

在表9所示序号1和序号2的工况下，按照上表改变模型中炸药的径高比，得到的约束方形靶板的中心挠度结果如图6所示。

由图6可以看出，炸药当量不变(700 g)时，随着炸药径高比的变大，靶板的中心挠度越来越大，但趋于平缓。

不同炸药当量，不同炸距，不同靶板厚度工况下，炸药形状对靶板中心挠度的影响如图7所示，表9所示序号3、序号4、序号5和序号6各工况下的参数如表10所示。

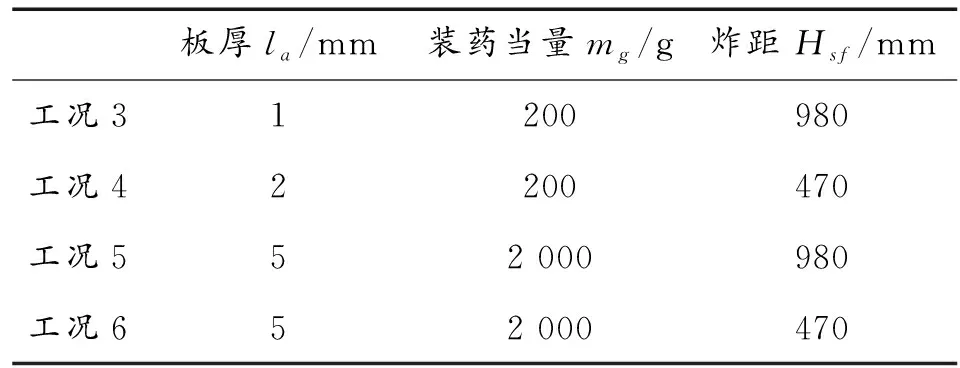
表10 工况参数

由图7可以看出，在各个工况下，随着炸药径高比的变大，靶板的中心挠度越来越大。在工况3下，曲线的斜率越来越小，直至平缓；在工况4、工况5、工况6下，曲线仍呈逐渐上升趋势。

5 结论

1) 通过对爆炸冲击作用下四边约束靶板结构响应的仿真计算与试验结果的对比分析，验证了ALE算法的准确性，修正了仿真参数，为后续仿真分析提供了理论基础。

2) 研究了在炸药当量为200 g、700 g和2 kg，炸距为980 mm、470 mm的不同工况下，炸药的径高比在1～5之间离散变化时，对靶板变形的影响。总体上，随着炸药径高比的变大，靶板的中心挠度越来越大，爆炸产生的空气冲击波的比冲量越大。当炸药当量较小且炸距较远，径高比达到一定值时，径高比的变化基本不影响靶板的中心挠度，对比冲量的影响较小；当炸药当量较大且炸距较近时，其径高比对中心挠度的影响显著，对比冲量的影响较大。

3) 选取的径高比范围具有一定的局限性，在更大范围内对爆炸冲击波比冲量的影响仍需继续研究。

[1] 宁建国，王成，马天宝.爆炸与冲击动力学[M].北京：国防工业出版社，2010.

[2] 王芳，冯顺山.爆炸冲击波作用下靶板的塑性大变形响应研究[J].中国安全科学学报，2003,13(3).

[3] 李金山.炸药圆柱体的热爆炸临界参数与其长径比的关系研究[J].含能材料，1995,3(1):34-37.

[4] 谷鸿平，柳雯，李广嘉.起爆方式对柱形炸药空爆冲击波场的影响[J].爆破，2016,33(4):34-38.

[5] 高轩能，吴彦捷.TNT爆炸的数值计算及其影响因素[J].火炸药学报，2015,38(3):32-39.

[6] NATO STANAG 4569.Protection Levels for Occupants of Logistic and Light Armored Vehicles[S].2004.

[7] BARNAT W.Experimental and numerical study of influence of incidence angle of shock wave created by explosive charge on the steel plate[J].Bulletin of The Polish Academy of Sciences Technical Sciences,2014,62(1):23-33.

[8] 张鑫磊，周云波，王显会，王宗千.浅埋炸药爆炸对靶板冲击的仿真方法对比研究[J].爆破，2016,33(4).

[9] Livermore Software Technology Corporation[Z].LS-DYNA keyword user’s manual，Livermore，California May 2007.

[10] LEE E，FINGER M，COLLINS W.JWL equation of state coefficients for high xplosive[R].Lawrence Livermore Laboratory，1973.

[11] 冯顺山，王芳，胡浩江.爆炸冲击波防护效应的评价方法研究[J].安全与环境学报，2004.

[12] 魏然.基于爆炸防护的车身结构多学科优化研究[D].南京：南京理工大学，2017.

[13] 华雨，于纪言，张庆，李兴隆.静爆冲击波在空气中的传播规律[J].兵器装备工程学报，2016(7)：168-172.