汽车轮毂抗冲击轮缘结构设计与工艺控制方法

张国智(新乡学院 机电工程学院，新乡 453003)

智能制造的意义不单单在强调技术，更是在强调节能、环保的制造理念，汽车作为近期无法淘汰的地面交通工具，未来必须要适应智能制造时代的节能和环保的发展理念，因而，关于汽车结构件的各方面的设计均涉及轻量化的问题[1]，对其的研究也已成为热点之一.随着研究的逐步深入，取得了一些研究成果，如：对车辆悬架系统的优化[2]、汽车驱动轴多目标轻量化优化设计[3]、汽车B柱优化设计[4]，镁合金在汽车车身轻量化设计中的应用[5]等.对于汽车而言，主要承载部件最为重要的就是轮毂，随着整车轻量化的要求，对轮毂的轻量化设计要求也逐渐严苛，同时，要求在结构不能大修改时还要保证其抗冲击性能，因而，关于其拓扑结构及工艺的优化控制的研究就十分重要.目前，关于此方面的研究尚不深入、系统，基于此，结合动静法和有限元分析方法，对轮毂轮缘的结构设计与工艺控制方法进行了深入、系统的研究.

1 门槛冲击实验简介

在测试轮毂抗冲击能力的实验是门槛实验，具体实验过程是：首先，将轮毂安装在车上，车以60 km/h的速度撞击与行进方向成60度的路障，路障为直径是200 mm的钢制圆柱，此路障一半露在地上，然后，当车冲过路障后卸下轮子，测量轮毂撞击处的轮缘凹陷值，以此来测试轮毂强度.轮毂的截面简图如图1所示，门槛实验简图如图2所示.

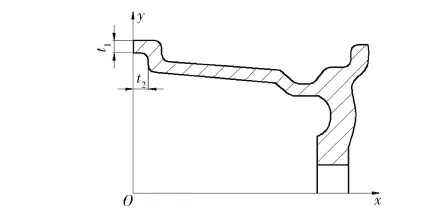
图1 轮毂截面简图

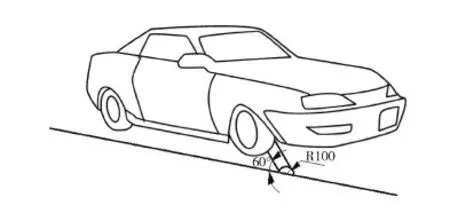
图2 轮毂门槛实验示意图

2 基于动静法的计算方案的提出

门槛实验是一个非常复杂的瞬间冲击性实验，过程复杂，而且，涉及到接触非线性、材料非线性、几何非线性多重非线性，整个过程的有限元仿真需要大量的计算时间，有限元模型的前处理建立也非常复杂，研究轮毂抗冲击性能的结构和工艺因素影响规律需要多次反复的动态有限元计算，因而，要得到相关的影响规律需要大量的计算时间.根据动静法，可将整个实验过程等效为一个静态过程，将动态冲击的冲击力作为静态计算的施加载荷而建立静态等效的非线性有限元模拟，因而，将有效地简化前处理过程，并且有效降低计算时间，冲击力可通过动态的冲击模拟、理论计算、实验测试得到，进而可快速而准确地得到轮毂抗冲击性能的结构和工艺因素影响规律，具体计算方案如图3所示.

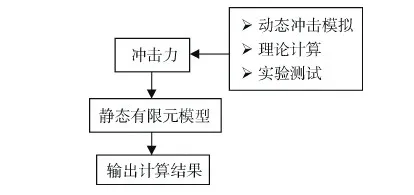
图3 门槛实验动静法的计算方案

3 有限元模型的建立与验证

3.1 有限元模型的建立

门槛实验的等效静力非线性的有限元模型图4所示.轮毂中间安装孔固定约束，门槛与轮胎表面呈30°角，约束门槛的水平与旋转自由度，在门槛上施加沿垂直方向的等效的冲击力，轮胎与轮毂、轮胎与门槛间建立非线性接触，轮胎内部施加0.2 MPa内压载荷，轮毂材料采用各向同性双线性硬化弹塑性材料模型，为了保证接触不丢失几何特征，轮胎与轮毂轮缘均采用六面体单元.

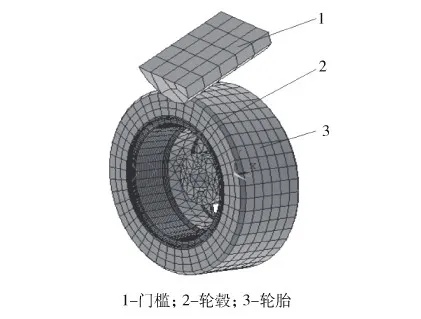
图4 有限元模型

3.2 有限元模型的验证

轮毂材料与几何主要参数如表1所示时，进行有限元分析，其有限元分析的变形结果如图5所示，在图5中显示放大倍数为10倍.门槛实验后，轮毂最大凹陷处的计算结果为5.24 mm，相对180°位置的径向突出变形量为1.05 mm，通过门槛实验测试，有限元计算结果与实测数据最大误差为7.73 %，由此可见等效的静力非线性有限元分析的计算结果是正确的.

表1 轮毂材料与几何主要参数

图5 轮毂冲击试验后的有限元分析的变形

4 轮缘抗冲击设计与工艺控制

4.1 轮缘抗冲击影响因素研究

当轮毂的材料参数如表1所示不变，仅结构参数t1、t2比表1中的名义值增大或减小20%时，轮缘凹陷曲线如图6所示.

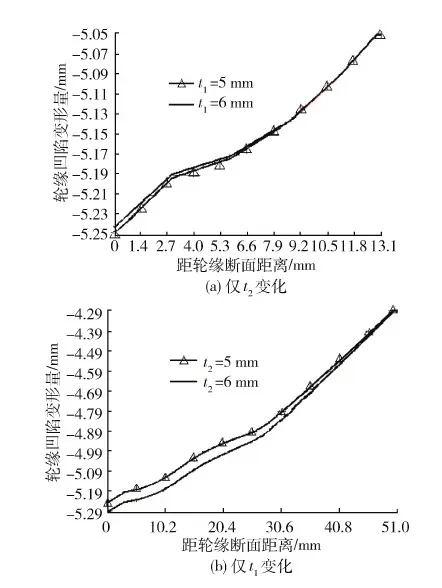
图6 几何参数变化时轮缘凹陷曲线

从图6(a)中可见，当仅t2值增大20%时，撞击后的轮唇处最大凹陷值增大了0.88%；从图6(b)中可见，当仅t1值减小20%时，撞击后的轮唇处最大凹陷值增大了0.13%.从图6中可见，t1、t2参数变化时轮缘凹陷曲线的变化规律不同，并且，结构参数t1、t2均变化10%时，t2对撞击后的轮唇处最大凹陷值影响较大.

当轮毂的几何参数如表1所示不变，仅材料参数σs、E、D比表1中的名义值增大或减小10%时，轮缘凹陷曲线如图7所示.

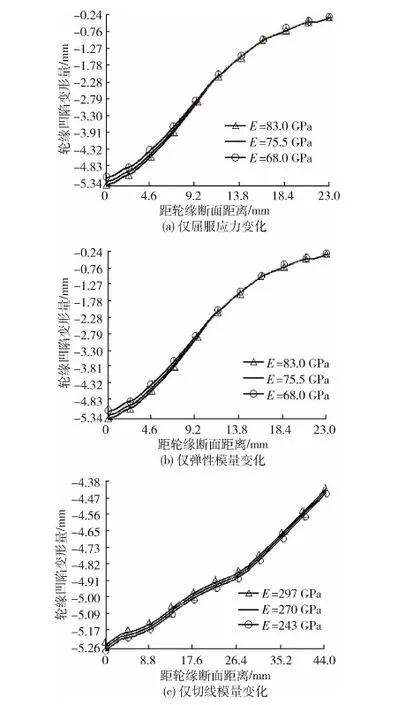
图7 材料参数变化时轮缘凹陷曲线

从图7(a)中可见，当仅屈服强度从152 Mpa减小到136.8 MPa时，撞击后的轮唇处的最大凹陷值增加了22.7%，而仅屈服强度从152 Mpa增加到167.2 MPa时，撞击后的轮唇处的最大凹陷值减少了19.5 %；从图7(b)中可见，当仅弹性模量从75.5 Gpa减小到68 Gpa时，撞击后的轮唇处的最大凹陷值减小了2.38 %，而当仅弹性模量从75.5 Gpa增加到83 Gpa时，撞击后的轮唇处的最大凹陷值增加了1.71%；从图7(c)中可见，当仅应变刚模数增大或减小10%时，撞击后的轮唇处的最大凹陷值减小或增大0.27 %，曲线对称性很好.从图7中可见，σs、E、D参数变化时轮缘凹陷曲线的变化规律不同，并且，当材料参数有10%波动时，屈服强度对撞击后的轮唇处最大凹陷值影响较大.

4.2 轮缘结构设计与工艺控制要点

综上可知，轮毂的轮唇结构尺寸及轮毂在热处理或其它对轮毂物理性能有较大影响的工艺方面对轮毂的轮缘抗冲击能力会影响很大.因此，在轮缘结构设计方面要严格控制轮唇长度和厚度，在减重方面，建议减小轮缘的厚度；在工艺控制方面，要严格控制屈服强度、弹性模量、切线模量3个材料参数，并且，要尤其注意严格控制屈服强度.

5 结 论

1) 在轮毂减重要求下，轮唇处在减小尺寸时应首先减小其厚度尺寸，而不要减小其长度尺寸，此种情况的减重在减掉相同体积材料下对轮毂的抗冲击性能影响较小.

2) 轮毂的材料性能参数对其轮缘的抗冲击性能影响较大，当结构尺寸减小到一定程度时，建议通过工艺控制来提高其材料性能进而通过门槛实验.

3) 轮毂轮缘的抗冲击性能与材料的塑性性能较为相关，尤其材料的屈服应力对轮毂的轮缘抗冲击性能影响最大.

通过本文的研究为轮毂的优化设计和工艺控制提供了分析方法和理论依据.

参考文献：

[1] 郭玉琴, 朱新峰, 杨 艳, 等. 汽车轻量化材料及制造工艺研究现状[J]. 锻压技术, 2015,40(3):1-6.

[2] 施 睿, 赵春霞. 双横臂独立悬架运动学分析与优化设计[J].车辆与动力技术, 2014(3):35-41.

[3] 朱发渊, 汪朝晖, 吕 密. 基于遗传算法的汽车驱动轴多目标轻量化优化设计[J].机械设计与制造,2015(3):87-90.

[4] 徐增密, 刘立忠, 申国哲, 等. 基于响应面和kriging 代理模型的汽车B柱优化设计[J]. 汽车技术,2012(4):39-43.

[5] 任兰柱, 董瑞君, 徐 洪, 等. 镁合金在汽车车身上的应用研究 [J]. 热加工工艺, 2016,45(10):30-32.