基于KFDD与进化算法的可逆电路优化算法
2018-07-03卜登立刘宇安
卜登立,刘 欢,刘宇安
(1.井冈山大学 电子与信息工程学院,江西 吉安 343009;2.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西 吉安 343009)
0 引 言
可逆计算是信息无损的计算模式,在量子计算等新兴技术领域有着重要应用。随着芯片制造工艺的发展,单个晶体管的尺寸接近原子规模,已经无法再通过缩小晶体管尺寸进一步降低功耗[1],再加上芯片复杂度的上升,功耗问题已经成为计算机芯片向更小更快方向发展的障碍[2]。信息无损的可逆计算可以实现理论上的近似零功耗[3],因此,越来越多的研究者也将可逆电路作为低功耗设计的一种替代方案[2,4]。
决策图(decision diagram, DD)作为函数高层次、层次化的表示模型,已被广泛应用于可逆电路的综合。用于可逆电路综合的DD有二元决策图(binary decision diagram, BDD)[5]、正Davio决策图(positive Davio decision diagram, PDD)[6]和Kronecker功能决策图(Kronecker functional decision diagram, KFDD)[7-8],其中,BDD仅对函数的输入变量进行香农分解,PDD仅对输入变量进行正Davio分解,而KFDD则对输入变量分别进行香农分解和正、负Davio分解,因此,BDD和PDD可以看作是特殊类型的KFDD。借助DD进行可逆电路综合属于结构化的综合方法[9],将DD结点视为构造块,根据所建立的可逆门库将结点函数综合为可逆子电路,并根据逻辑关系进行可逆子电路的级联,从而实现可逆电路的综合[5]。因此,DD的结点数将影响由之综合所得可逆电路的成本。输入变量的顺序以及输入变量的分解类型对KFDD的结点数均有影响[10],不同的输入变量顺序和不同的输入变量分解类型有可能得到不同大小的KFDD,也会得到具有不同量子成本和量子位数的可逆电路。基于KFDD的可逆电路优化方法借助Sifting技术来改变输入变量的顺序和分解类型进行可逆电路的量子成本优化或者量子位数优化[11],仅搜索了解空间中的部分区域,难以保证得到全局最优解。因此,为在借助KFDD进行可逆电路综合时能够得到全局最优解,需要使用全局优化算法进行可逆电路优化。
本文在可逆电路的KFDD综合方法基础之上,针对KFDD的输入变量分解类型和输入变量顺序问题,设计基于进化算法的可逆电路优化算法。该算法通过优化KFDD输入变量的分解类型以及顺序来实现可逆电路的优化,分别采用离散值和整型值编码输入变量的分解类型和顺序,利用遗传算法进行搜索,并设计策略来避免过早收敛问题。给出了算法描述,并使用一组RevLib函数[12]对算法进行了验证。
1 可逆电路的KFDD综合方法
对于n输入变量的函数f(xi|1≤i≤n),其KFDD是由依次对函数f的n个输入变量分别实施的香农分解和正、负Davio分解得到[13]
(1)
KFDD使用终端结点表示常量,非终端结点表示变量,称之为变量结点,每个变量结点有2个子结点,左子结点Vl和右子结点Vh,Vl,Vh∈V。补边的采用有助于降低KFDD的复杂度,而标准形表示的KFDD仅允许连接Vk与Vh的边Ek,h∈E为补边[13]。现假设结点Vk是xi变量结点,其结点函数为Fk,Vl的结点函数为Fl,Vh的结点函数为Fh,那么根据变量xi的分解类型di,以及Ek,h是否为补边,Fk可以由Fl和Fh来描述,如表1所示。

表1 Vk结点函数描述Tab.1 Node function of Vk

可逆电路的KFDD综合方法通过深度优先遍历G,逐结点综合,根据Vk的结点函数将Vk综合为可逆子电路,再级联所有的子电路实现可逆电路的综合[14]。借助KFDD进行可逆电路综合的算法如算法1所示。
算法1可逆电路综合算法。
1)QC←0,QB←n;
2)深度优先方式访问G;
3)对每一个Vk∈V,根据Fk从NCT门库中选取可逆门,并通过适当增加Lk条辅助线将之级联为可逆子电路,统计量子成本和量子位数:QC←QC+QCk,QB←QB+Lk;
4)级联所有的子电路从而构建实现函数f的可逆电路。
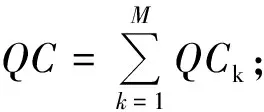
2 基于进化算法的可逆电路优化算法
输入变量的顺序以及分解类型会影响KFDD的结点数量,从而影响由算法1综合所得可逆电路的量子成本和量子位数。因此,可逆电路成本优化问题可以转化为输入变量顺序以及输入变量分解类型优化问题。
函数有n个输入变量,每个输入变量的分解类型有3种,因此,可逆电路成本优化的解空间大小为3n×n!。本文在大小为3n×n!的解空间内进行全局搜索,搜索成本最小的可逆电路。
2.1 进化算法模型
遗传算法具有与问题域无关、并行潜质以及搜索过程简单等特点[16],因此,本文基于遗传算法模型设计进化算法。
2.1.1 适应度函数
可逆电路的成本包括量子成本QC和量子位数QB,本文在进行可逆电路优化时将量子成本作为主要优化目标,而量子位数则作为次要优化目标,即先比较2个电路解Si与Sj的量子成本QC(Si)与QC(Sj),如果量子成本相同,再比较2个解的量子位数QB(Si)与QB(Sj)。本文可逆电路优化所采用的成本函数为
(2)
可逆电路优化是成本最小化问题,因此,本文进化算法所采用的适应度函数如(2)式所示。
2.1.2 遗传编码
个体的遗传编码分为2个部分:D=[d,v],其中d=[d1,d2,…,dn]为输入变量分解类型列表,采用离散值编码di∈{0,1,2},分别表示输入变量的分解类型为香农分解和正、负Davio分解;v=[v1,v2,…,vn]为输入变量顺序,vj∈[1,n],采用整型值编码,变量顺序属于置换码。遗传编码中d和v的编码长度都为n,遗传编码的总长度为2×n。
2.1.3 遗传算子
遗传算子包括选择、交叉、变异和再生。选择采用锦标赛选择策略,假设锦标赛规模为T:在种群中随机抽取T个个体,然后选择其中的最优个体作为后续交叉运算的父个体。
为遗传编码中的分解类型列表d和变量顺序v设计不同类型的交叉运算。对于d,采用单点交叉:随机生成一个位置c1(1≤c1≤n),对2个父个体中的d进行交叉;对于v,为保证实施交叉运算后能够得到有效的变量顺序,采用基于顺序的交叉(order-based crossover)[17]:随机生成2个位置c1和c2(1≤c1,c2≤n),将父个体1和2遗传编码的v中位于c1和c2之间的基因分别复制到子个体1和2遗传编码的v,而子个体1和2遗传编码的v中其余的基因则分别通过扫描父个体2和1遗传编码的v来进行填充,正向扫描和逆向扫描会得到不同的结果,如图1所示。

图1 基于顺序的交叉运算举例Fig.1 Example for order-based crossover
变异运算则采用交换变异[18]:随机生成2个不同位置c1和c2(1≤c1,c2≤n),将位于c1和c2的基因交换。基因编码中的d和v独立实施交换变异运算,图2给出了基因编码中的v在c1=1和c2=3时的交换变异运算。

图2 交换变异运算举例Fig.2 Example for swap mutation
再生采用稳态再生策略,经选择、交叉、变异运算后生成新种群,并将上一代种群的最佳个体与新种群的最差个体进行竞争替换,然后将新种群作为下一代种群。
2.1.4 进化算法描述
根据以上所述的适应度函数、遗传编码以及选择、交叉、变异和再生运算,设计如算法2所示的进化算法,算法2仅给出了一次进化过程。其中,P表示种群,Pi和Qi均表示个体,Pi.D表示个体Pi的遗传编码,Pi.QC和Pi.QB分别表示个体Pi所对应可逆电路的量子成本和量子位数。
算法2进化算法。
输入:上一代种群P={Pi|1≤i≤|P|}。
输出:下一代种群P。
2)for(i←1;i≤|P|;i←i+2) {
3)k←tour_select(P);l←tour_select(P);
4)cross(Pk.D,Pl.D,Qi.D,Qi+1.D);
5)mut(Qi.D);mut(Qi+1.D);
6)eval(Qi.D);eval(Qi+1.D);
8) if(Po.QC (Po.QC=Qw.QC∧Po.QB 9)Qw←Po; 10)P←; 算法2中的|P|表示种群P中的个体数,为个体集合,作为进化过程中的新种群。tour_select为锦标赛选择函数,需要进行2次锦标赛选择,得到种群P中2个个体的索引k和l;cross为交叉函数,遗传编码D中的d和v分别以交叉概率pc实施单点交叉和基于顺序的交叉运算,在实施v的交叉运算时,分别以0.5的概率进行正向扫描和逆向扫描;mut为变异函数,编码D中的d和v分别以变异概率pm实施交换变异运算。eval为成本计算函数,根据Qi.D中的输入变量分解类型列表d和输入变量顺序v改变KFDD图G中输入变量的分解类型和输入变量顺序,然后运行算法1计算可逆电路的量子成本QC和量子位数QB,关于如何改变G中输入变量的顺序以及输入变量的分解类型请参阅文[13]。算法2的第8)至10)步则进行种群再生,第8)和9)步使用上一代种群P中的最优个体Po与新种群中的最差个体Qw进行竞争,第10)步则形成下一代种群P。锦标赛选择、种群中最优个体和最差个体的判定都采用了如(2)式所示的判定方法。 虽然遗传编码D中的d和v作为2个部分独立进行交叉和变异运算,但在计算个体对应可逆电路的成本时却同时使用这两部分,因此,所设计的进化算法同时解决了输入变量顺序问题和输入变量分解类型问题。 种群多样性的缺失是导致遗传算法过早收敛的重要原因。为维持种群多样性,在搜索过程的前期阶段,采用小生境方法,划分多个子群,每个子群搜索解空间中的不同区域,扩大搜索空间。但是随着子群搜索的进行,各个子群内的个体逐渐趋同,容易导致算法陷入局部极小。因此,为避免算法陷入局部极小,在搜索过程的后期阶段,将多个子群合并为整体种群,利用整体种群进行集中搜索。子群的搜索以及整体种群的搜索均采用如算法2所示的进化算法模型。本文基于KFDD和进化算法的可逆电路优化算法如算法3所示。 算法3可逆电路优化算法。 1)读取函数,转换为KFDD图G; 2)初始化算法参数,包括子群数s,子群规模Ns,锦标赛规模T,交叉概率pc和变异概率pm,子群搜索最大迭代次数t1,整体种群搜索最大迭代次数t2; 3)迭代次数变量t←0,随机生成s个子群{Pi|1≤i≤s},每个子群Pi包含Ns个个体,并计算每个个体所对应可逆电路的量子成本和量子位数; 4)对每一个子群Pi,运行算法2;t←t+1; 5)如果t≤t1,转步骤4);否则转步骤6); 6)P←∪{Pi|1≤i≤s};t←0; 7)对整体种群P运行算法2;t←t+1; 8)如果t≤t2,转步骤7);否则转步骤9); 9)得到种群最优Po∈P; 10)根据Po.D中的d和v改变G中输入变量的分解类型以及输入变量的顺序; 11)运行算法1将G综合为可逆电路。 算法3的第3)-5)步为子群搜索阶段,第6)-8)步为整体种群搜索阶段,整体种群P的种群规模为s×Ns。算法3已在可逆逻辑综合工具RevKit[11]中实现,关于第1)步中如何由函数构建KFDD以及第10)步的详情请参考文献[11,13]。 算法3采用C++语言实现,在Linux操作系统下使用g++编译器编译。算法参数通过对一组RevLib函数[12]进行可逆电路优化并对结果进行评价确定:子群数s=6,子群规模Ns=10,锦标赛规模T=5,交叉概率pc=0.6,变异概率pm=0.4,子群搜索最大迭代次数t1=100,整体种群搜索最大迭代次数t2=50。 为验证算法3,在配置为Intel Core i3-2350M CPU 6GB RAM的个人计算机上对14个RevLib函数进行可逆电路优化,并与RevKit[11]中使用Sifting技术的基于KFDD的可逆电路优化算法(称之为RevKit_KFDD算法)的结果进行比较,结果如表2所示,其中,“I/O”表示函数的“输入数/输出数”。 由于算法3具有一定随机性,因此,对每个函数都使用算法3进行50次优化,并统计50次优化所得结果的最小值和平均值,如表2中的第5和6列所示的QB的最小值和平均值,以及第7和8列所示的QC的最小值和平均值,同时统计50次算法3运行所需CPU时间的平均值,如表2第9列所示,时间的单位是秒。而表2中的“Imp”则表示对每个函数,相对于算法RevKit_KFDD的结果,算法3的“平均”结果分别将量子位数和量子成本减少的百分比。 表2 可逆电路优化结果Tab.2 Optimization results for reversible circuits 由表2可以看出,对于这些函数,算法3结果QB的均值都非常接近于QB的最小值,QC的均值也比较接近于QC的最小值。将算法3结果QB和QC的均值分别与RevKit_KFDD算法结果的QB和QC进行比较可以看出,对于所有函数而言,算法3均能够减少量子成本,最大减少了51.05%(函数radd_193),最小减少了4.03%(函数hwb8_64);对于大部分函数而言,算法3能够减少量子位数,只有3个函数,算法3结果的量子位数有所增加,这是因为算法3将量子成本作为主要优化目标,量子位数作为次要优化目标,而“基于KFDD进行可逆电路综合,可逆电路在量子位数和量子成本之间存在着折中”。从表2最后一行的平均结果来看,相对于RevKit_KFDD算法,算法3将量子位数减少了6.21%,量子成本减少了12.67%,这验证了算法3的有效性。 表2也给出了算法3对每一个函数优化50次所需时间的平均值。对于大部分函数,算法3所需时间均小于10 s,有2个函数:clip_124和hwb8_64,尽管其输入变量数小于10,但是算法3运行花费的时间却相对较多,这是因为这2个函数在优化过程中算法3所搜索到的KFDD的结点数相对较多,导致在优化过程中改变KFDD中输入变量的顺序和分解类型所花费的时间较长。 为进一步对算法3进行评价,统计了算法3对每一个函数优化50次所得结果的变异系数(coefficients of variation, CV),CV=结果标准差×100/结果平均值,用来评价算法结果的稳定性[19]。结果如图3所示。 图3 算法3结果的变异系数Fig.3 CV of results obtained by algorithm 3 由图3可以看出,对于表2中的函数,算法3结果的变异系数均较小,QC结果的最大变异系数仅为5.95%(函数pcler8_190),QB结果的最大变异系数仅为3.8%(函数pcler8_190),这说明算法3有较好的结果稳定性。 图4给出了算法3优化函数clip_124时的收敛曲线。 图4 算法3优化函数clip_124的收敛曲线Fig.4 Convergence curve of algorithm 3 when optimizing clip_124 图4中的第1~100次迭代是子群搜索阶段,第101~150次迭代是整体种群搜索阶段。由图4可以看出,由于算法3在前期阶段利用多个子群同时搜索解空间中的不同区域,因此,算法3具有较快的收敛速度。在子群搜索阶段,算法3在第33次迭代搜索到量子成本为431(量子位数为58)的局部最优解,第66次迭代搜索到量子成本为431、量子位数为57的局部最优解,并且到子群搜索阶段结束时(第100次迭代),寻优结果的量子成本和量子位数一直没有得到改善,算法3陷入了局部极小。当算法3进入整体种群搜索阶段,在整体种群搜索的第6次迭代(图4中的第106次迭代)搜索到量子成本得到改善的解(量子成本为423,量子位数为58),并且在整体种群搜索的第14次迭代,算法3开始收敛于量子成本为417、量子位数为58的最优解。这验证了算法3所采用的“在搜索的前期阶段利用多个子群进行搜索,扩大搜索空间,而在搜索的后期阶段利用整体种群进行集中搜索”策略的有效性。 可见,算法3具有较强的全局寻优能力,并且有较好的结果稳定性,能够降低由KFDD综合所得可逆电路的量子成本和量子位数。 文献[20]设计了一种结合Reed-Muller逻辑与DD模型进行可逆电路优化的Reed-Muller decision diagram synthesis,RMDDS算法。该算法通过对Reed-Muller逻辑进行分解并借助BDD和KFDD进行可逆电路优化,同时,在NCT门库的基础之上结合基本Peres门来改善可逆电路的量子成本。使用RMDDS算法对表2中的函数进行了可逆电路的量子成本优化,结果如表3所示。其中,“Imp”表示对每个函数相对于RMDDS算法的结果,表2中算法3的“平均”结果分别将量子位数和量子成本减少的百分比。 从表2和表3中的量子位数角度来看,有7个函数算法3结果的量子位数优于RMDDS,另外7个函数RMDDS结果的量子位数优于算法3,从平均角度来看,RMDDS结果的量子位数略占优势。但从量子成本角度来看,在这14个函数中,仅有2个函数算法3的结果劣于RMDDS的结果,对于其他函数,算法3的结果均优于RMDDS的结果。从表3最后一行的平均角度来看,与RMDDS相比,算法3尽管使量子位数增加了2.70%,但却将量子成本降低了16.34%。从时间角度来看,对于绝大多数电路,算法3均有较高的时间效率,从时间的平均角度看,与RMDDS相比,算法3的时间效率提高了一个数量级。 表3 RMDDS算法结果Tab.3 Results of RMDDS algorithm 综上所述,本文所设计的基于进化算法的可逆电路优化算法具有较强的全局寻优能力,能够降低可逆电路的量子成本。 可逆逻辑在量子计算以及低功耗电路设计等领域中的重要应用,使得可逆电路的综合与优化得到了广泛关注,降低可逆电路的成本则有助于进一步推动可逆电路的应用。本文在可逆电路的KFDD综合方法基础之上,通过优化KFDD的输入变量顺序和输入变量分解类型来进行可逆电路的成本优化,并设计了基于进化算法的可逆电路优化算法。使用一组RevLib函数对所设计算法进行了验证,结果表明,所设计算法具有较强的全局寻优能力,并有较好的结果稳定性,能够降低可逆电路的量子成本。 参考文献: [1] MACK C. Themultiple lives of Moore's law [EB/OL]. [2015-12-20]. http://spectrum.ieee.org/semiconductors/processors/the-multiple-lives-of-moores-law. [2] CAMPOS-AGUILLN C O, CELIS-CORDOVA R, HNNINEN I K, et al. A mini-MIPS microprocessor for adiabatic computing[C]//IEEE. Proceedings of the IEEE International Conference on Rebooting Computing. San Diego, CA: IEEE Press, 2016: 1-7. [3] BENNETT C H. Logical reversibility of computation[J]. IBM Journal of Research and Development, 1973, 17(6): 525-532. [4] MORRISON M, RANGANATHAN N. Synthesis of dual-rail adiabatic logic for low power security applications[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2014, 33(7): 975-988. [5] WILLE R, DRECHSLER R. BDD-based synthesis of reversible logic for large functions[C]//ACM. Proceedings of the 46th ACM/IEEE Design Automation Conference. San Francisco, CA: ACM Press, 2009: 270-275. [6] PANG Y, YAN Y, LIN J, et al. An efficient method to synthesize reversible logic by using positive Davio decision diagrams[J]. Circuits, Systems, and Signal Processing, 2014, 33(10): 3107-3121. [7] SOEKEN M, WILLE R, DRECHSLER R. Hierarchical synthesis of reversible circuits using positive and negative Davio decomposition[C]//IEEE. Proceedings of the 5th IEEE International Design and Test Workshop. Abu Dhabi: IEEE Press, 2010: 143-148. [8] 王友仁, 沈先坤, 周影辉. 基于KFDD的可逆逻辑电路综合设计方法[J]. 电子学报, 2014, 42(5): 1025-1029. WANG Youren, SHEN Xiankun, ZHOU Yinghui. Synthesis design method of reversible logic circuit based on Kronecker functional decision diagram[J]. Acta Electronic Sinica, 2014, 42(5): 1025-1029. [9] ZULEHNERA, WILLE R. Skipping embedding in the design of reversible circuits[C]//IEEE. Proceedings of the IEEE 47th International Symposium on Multiple-Valued Logic. Novi Sad: IEEE Press, 2017: 173-178. [10] BECKERT B, DRECHSLER R, THEOBALD M. OKFDDs versus OBDDs and OFDDs[C]//Springer. Proceedings of the 22nd International Colloquium on Automata, Languages and Programming. London, UK: Springer Press, 1995: 475-486. [11] SOEKEN M, FREHSE S, WILLE R, et al. RevKit: an open source toolkit for the design of reversible circuits[J]. Lecture Notes in Computer Science, 2012(7165): 64-76. [12] WILLE R, GROßE D, TEUBER L, et al. RevLib: an online resource for reversible functions and reversible circuits[C]//IEEE. Proceedings of the 38th IEEE International Symposium on Multiple-Valued Logic. Dallas, TX: IEEE Press, 2008: 220-225. [13] DRECHSLER R, BECKER B. Ordered Kronecker functional decision diagrams - a data structure for representation and manipulation of Boolean functions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1998, 17(10): 965-973. [14] SCHONBORN E, DATTA K, WILLE R, et al. Optimizing DD-based synthesis of reversible circuits using negative control lines[C]//IEEE. Proceedings of the 17th IEEE International Symposium on Design and Diagnostics of Electronic Circuits & Systems. Warsaw: IEEE Press, 2014: 129-134. [15] NIELSEN M A, CHUANG I L. Quantum computation and quantum information[M]. 10th anniversary edition. New York: Cambridge University Press, 2010. [16] 袁琴琴,吕林涛. 基于改进蚁群算法与遗传算法组合的网络入侵检测[J].重庆邮电大学学报: 自然科学版, 2017, 29(1): 84-89. YUAN Qinqin,LV Lintao. Network intrusion detection method based on combination of improved ant colony optimization and genetic algorithm[J]. Journal of Chongqing University of Post and Telecommunications: Natural Science Edition, 2017, 29(1): 84-89. [17] BURKE E K, KENDALL G. Search methodologies: introductory tutorials in optimization and decision support technique[M].New York: Springer Press, 2005. [18] FINDER A, DRECHSLER R. An evolutionary algorithm for optimization of pseudo Kronecker expressions[C]//IEEE. Proceedings of the 40th IEEE International Symposium on Multiple-Valued Logic, Barcelona: IEEE Press, 2010: 150-155. [19] 卜登立. 基于SADPSO的MPRM最小化算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(2): 226-232. BU Dengli.MPRM minimization algorithm based on SADPSO[J]. Journal of Chongqing University of Post and Telecommunications: Natural Science Edition, 2016, 28(2): 226-232. [20] LIN C C, JHA N K. RMDDS: Reed-Muller decision diagram synthesis of reversible logic circuits[J]. ACM Journal on Emerging Technologies in Computing Systems, 2014, 10(2):14:1-14:25.2.2 可逆电路优化算法描述
3 算法验证及结果分析
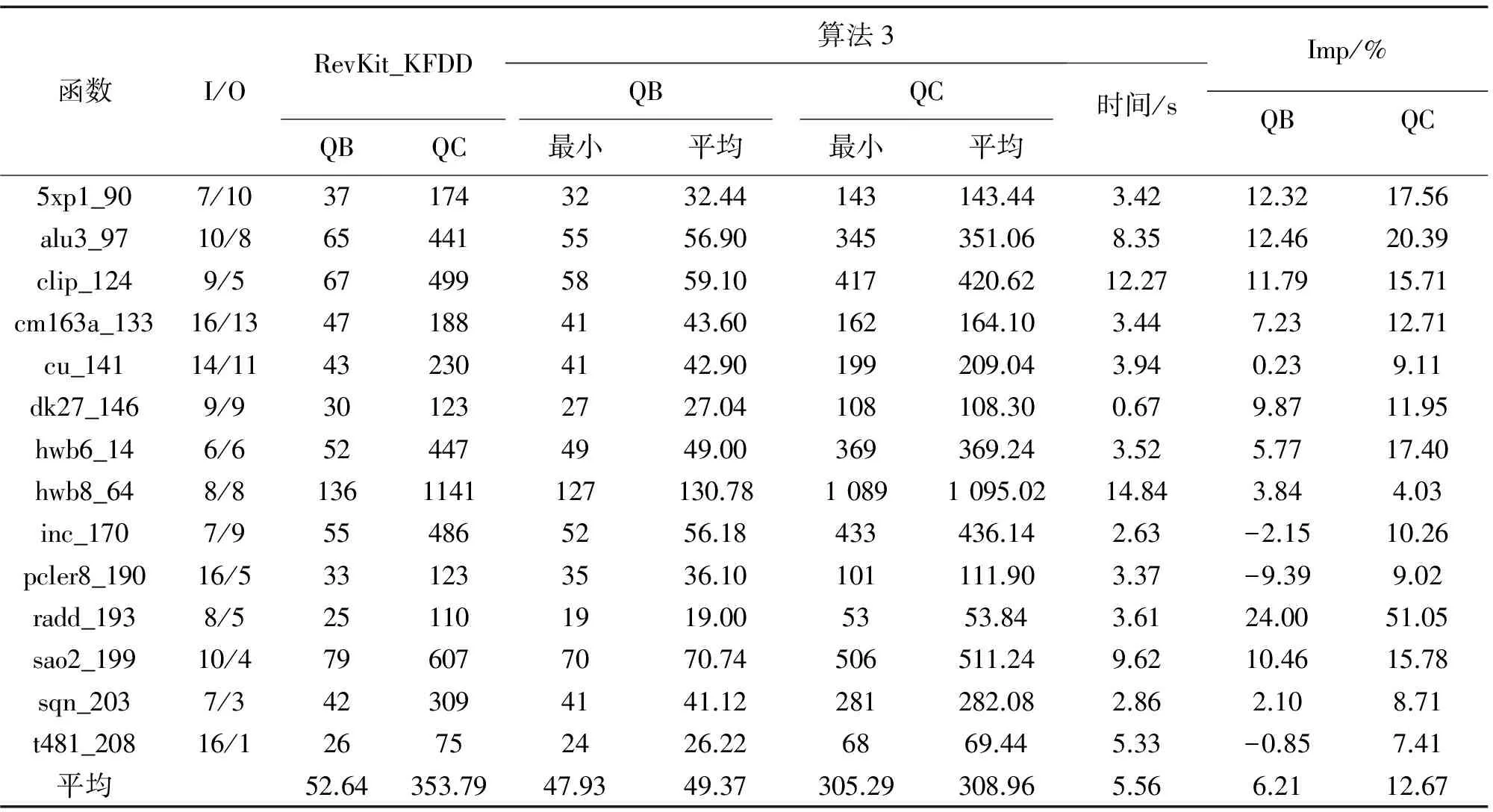
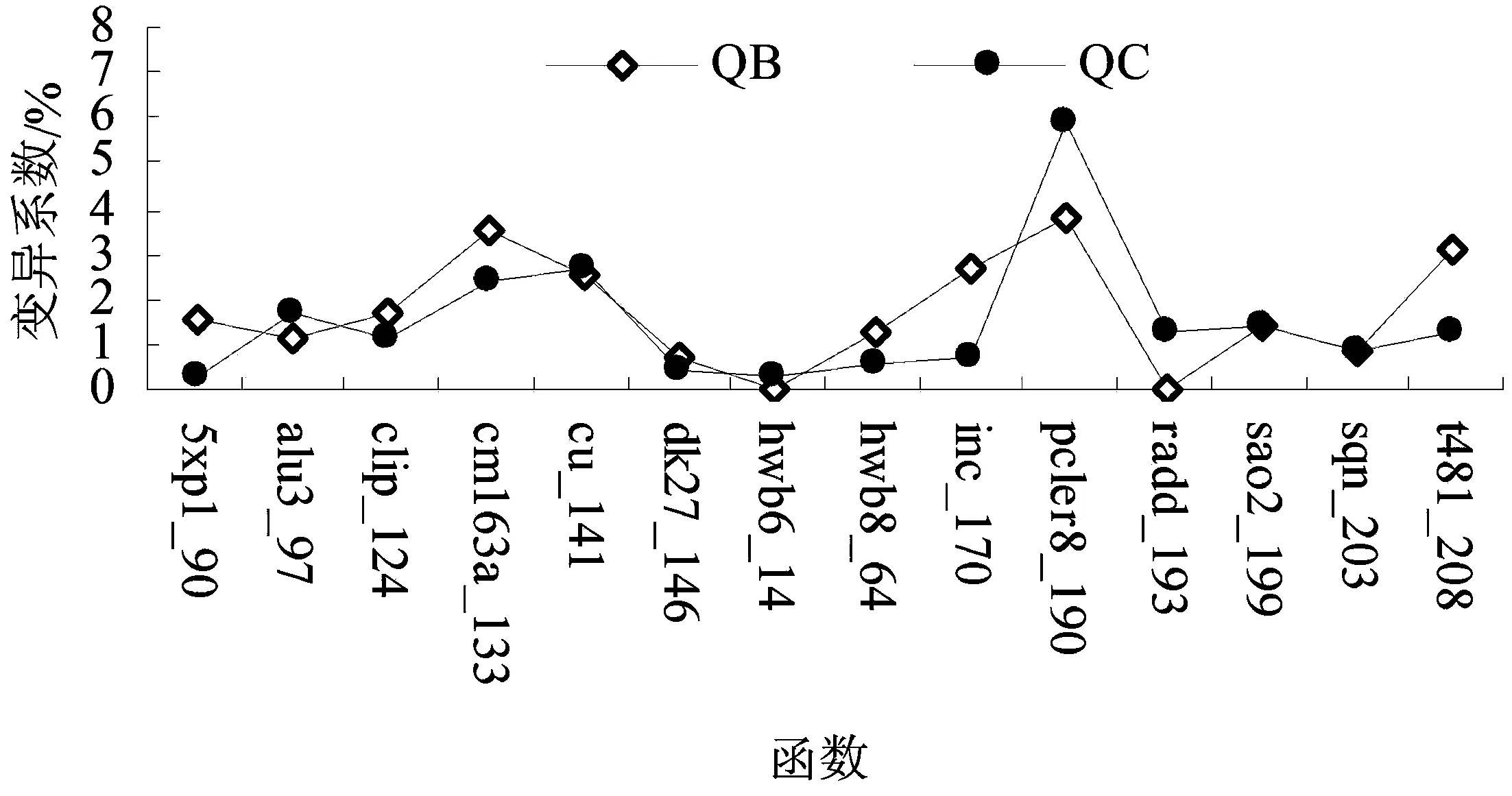

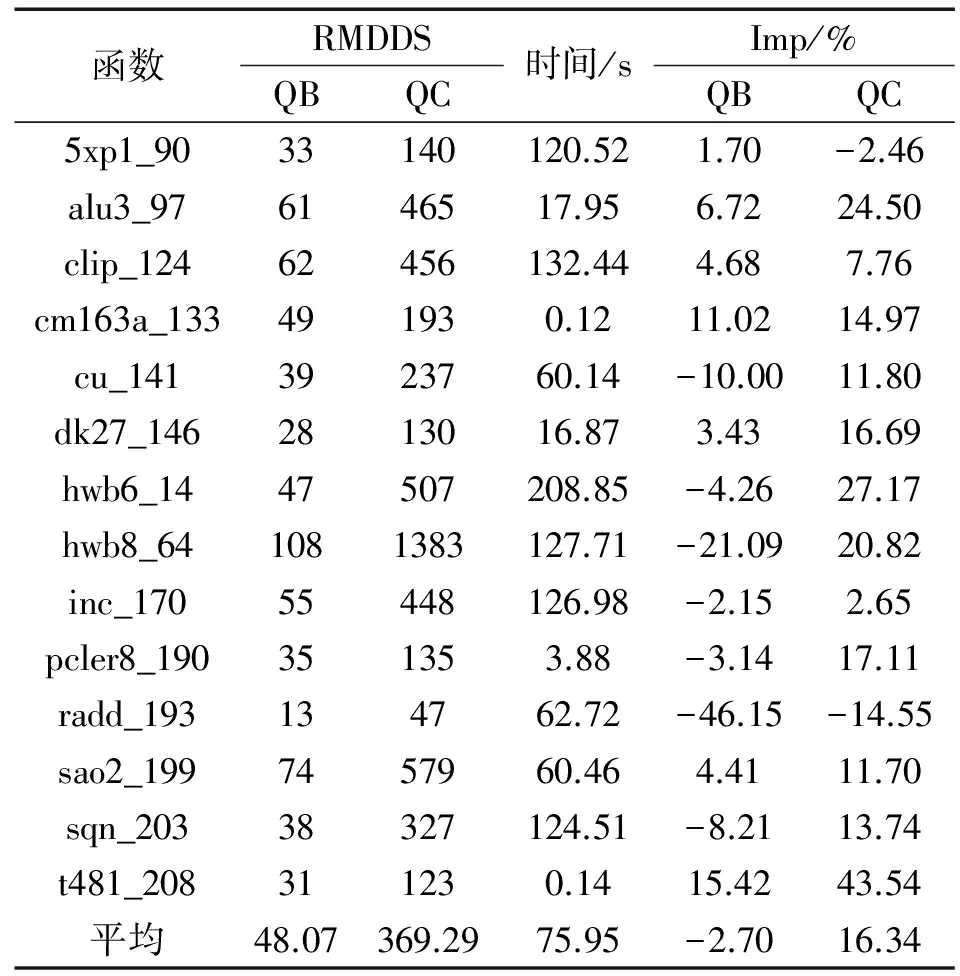
4 结束语
