双L型阵列的二维DOA估计方法

杨晋生，柳建飞，陈为刚

(天津大学 微电子学院，天津 300072)

0 引 言

对入射信号的二维波达方向估计是阵列信号处理中的一个基本问题，也是雷达、无线通信等许多领域的重要任务之一。二维到达角(direction-of-arrival, DOA)估计的性能取决于天线阵列的结构配置和所选择的算法[1]。文献[1]分析了几种常见的天线阵列形式的性能表现，其中,双L型阵列具有更低的克拉美罗界(cramer rao bounds, CRB)，在进行联合角度估计时具有更大的优势。典型的DOA估计方法包括二维多重信号分类(multiple signal classification, MUSIC)[2]、旋转不变技术的参数估计(estimation of signal parameters via rotational invariance technology, ESPRIT)[3]、平行因子技术[4]、高阶累计量法[5]、基于压缩感知的方法[6]、传播算子的方法等。其中以MUSIC和ESPRIT算法最为经典，但MUSIC算法需要进行谱峰搜索，而ESPRIT算法则需要对接收数据矩阵进行奇异值或者特征值分解，两者的计算复杂度都比较高。

基于传播算子的方法利用线性运算代替特征分解，计算量较小，因此，受到广泛研究[7-12]。在文献[8]中，Marcos将传播算子(propagator method,PM)算法应用到一维DOA估计中，无需对接收数据进行特征值或者奇异值分解，降低了计算复杂度。基于双平行线阵，Wu[9]将基于扩展PM算法扩展到2-D DOA估计中，不需要搜索谱峰的步骤，但是存在角度估计失效问题。Tayem[10]将PM算法推广到L型和双L型阵列中，解决了角度估计失败的问题，提高了估计性能，但是不能对二维角度自动配对，并且存在阵元信息损失问题。文献[11]在双平行线阵中提出了一种扩展孔径的PM算法，更加有效地利用了阵元的输出数据信息，并且无需额外的配对算法，具有更低的计算复杂度，但是仍然存在角度估计失败问题。为了解决文献[11]中算法存在的问题，Chen[12]基于三平行线阵提出了一种改进的DOA算法，提高了俯仰角的估计性能。以进一步降低计算量为目的，文献[13]提出了一种特殊结构的双平行线性阵列，将欧拉方程引入到PM算法中，可以实现角度自动配对。通过利用阵列流形矩阵的共轭对称性增加阵列的有效孔径[14]，Dong提出了一种计算量较低并且可以自动配对的估计方法，该方法通过结合PM算法和ESPRIT算法来获得二维DOA估计。文献[15]基于L型阵列提出一种利用互相关矩阵来消除噪声干扰的计算方法，对互相关矩阵进行一些线性运算便可获得角度信息，有效降低了计算量。文献[16]首先构造互相关矩阵消除噪声干扰，然后通过利用传播算子的方法进行角度估计，并且实现了角度的自动配对。

针对文献[10]中出现的阵元信息损失问题，本文通过利用双L型天线阵列的结构特征，提出一种新的子阵划分方法，使得对俯仰角和方位角估计时都能够利用水平方向和垂直方向的阵元信息。同时，这种子阵划分方法可以降低协方差矩阵中的冗余数据，比文献[10]中的方法具有更低的计算复杂度。为了避免阵列孔径损失，本文将文献[11]在双平行线阵中提出的扩展孔径的PM方法思想应用到双L型阵列的角度估计中。由于在角度估计时能充分利用阵元信息并且避免阵列孔径损失，因此，估计误差小。本文提出的方法虽然需要额外的配对算法，但是角度估计精度高，计算量小，对不同信噪比和不同角度组合的鲁棒性较好，具有一定的实用性。

1 DOA估计算法模型

1.1 阵列结构和信号模型

阵列结构如图1所示，本文采用双L型均匀线性阵列。3条均匀线性正交阵列分布在x,y,z轴上，每个轴上有M个阵元，位于原点的阵元是参考阵元，每个轴上相邻阵元之间的间距都是d。

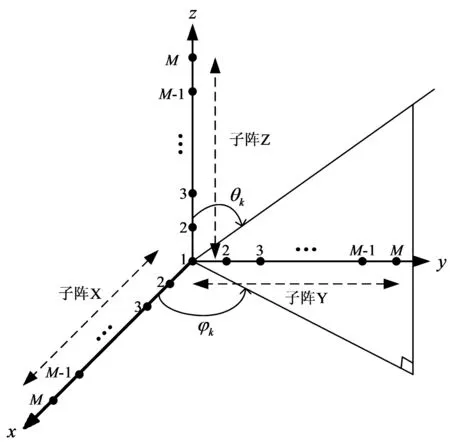
图1 双L型均匀线性阵列结构Fig.1 Two L-shaped uniform linear array configuration

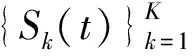
Ax=[ax(θ1,φ1),ax(θ2,φ2),…,ax(θK,φK)]

Ay=[ay(θ1,φ1),ay(θ2,φ2),…,ay(θK,φK)]

(1)

Az=[az(θ1,φ1),az(θ2,φ2),…,az(θK,φK)]

(1)式中，

(2)

则3个子阵列的阵元输出数据表达式为

X(t)=AxS(t)+Wx(t)

Y(t)=AyS(t)+Wy(t)

(3)

Z(t)=AzS(t)+Wz(t)

在t时刻，观测得到子阵X,Y,Z的接收数据矢量分别表示为X(t)=[x1(t),x2(t),…,xM(t)]T,Y(t)=[y1(t),y2(t),…,yM(t)]T和Z(t)=[z1(t)，…z2(t)…zM(t)]T。入射到天线阵列上的K个信号源的矢量表达式为S(t)=[s1(t),s2(t),…,sK(t)]T。噪声矢量表示为Wi(t)=[wi,1(t),wi,2(t),…,wi,M(t)]T(其中，i指x,y,z)。假定各阵元受到的噪声是均值为零、方差为σ2的加性复高斯白噪声，且与入射信号不相关。

1.2 传播算子方法

假设A为阵列流形矩阵，将A分块

(4)

(4)式中，矩阵A1和A2的维度分别为K×K和(M-K)×K。假设A1为非奇异矩阵，即A1的前K行独立，那么A2是A1的线性变换，有

A2=PHA1

(5)

PK×(M-K)为传播算子，令QH=[PH,-IM-K]，则有

QHA=0(M-K)×K

(6)

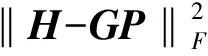
(7)

求出传播算子之后，再根据Q构造PM算法空间方位谱

FPM=aHQQHa

(8)

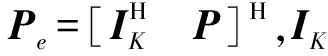
(9)

分别用Pa和Pb表示Pe的前M-1行和后M-1行，用Aa和Ab表示A的前M-1行和后M-1行，则有

(10)

则有以下关系式

(11)

通过(11)式便可求出包含角度信息的矩阵Φr。文献[12]则将文献[11]提出的扩展孔径的传播算子方法应用到三平行阵列中，提高了俯仰角的估计性能。为了解决文献[10]中存在的阵元信息损失问题，本文将此扩展孔径的传播算子方法应用到双L型阵列的角度估计中，有效提高了角度估计的精度。

2 基于改进传播算子的二维DOA估计

首先根据阵列结构特点，将双L型阵列虚拟地按2个独立的L型阵列进行分析，即位于xoz平面的L型阵列和位于yoz平面的L型阵列，并对每一个L型阵列的子阵列数据进行重排整理。与文献[10]中划分子阵和构造阵元数据接收矩阵的方式不同，本文的划分方式可以充分利用阵元输出数据的有效信息，同时又避免出现孔径损失的问题。然后通过利用文献[11]中提出的基于扩展孔径的传播算子方法得到传播算子，进而可以求得4个包含角度信息的旋转矩阵。由于2个虚拟L型阵列存在一个公共子阵Z，可以利用求最小范数的方法对2个旋转矩阵的元素配对。最后利用配对后的信息联合估计信号的俯仰角和方位角。

2.1 子阵划分

本文对接收数据矩阵X和Y做如下的处理得到2个新的矩阵Xd和Yd

Xd=JMX

Yd=JMY

(12)

(12)式中，JM=[0(M-1)×1,I(M-1)×(M-1)],I(M-1)×(M-1)是反对角线上全为1且其余元素全为0的选择矩阵。为了能在构造协方差矩阵时能利用所有的阵元数据并且使阵元数据不存在重叠，构造2个新的接收数据矩阵C和Q如下

(13)

文献[10]提出的方法将整个天线阵列分解成3个均匀线性阵列，通过z轴的阵列独立估计求俯仰角的信息，通过x轴和y轴的阵列获取方位角的信息，这种求解方式不能够充分利用阵元信息。为了获取角度信息，每个轴的阵列又划分为2个最大重叠的子阵，但这种划分方式在求解协方差矩阵时会有较大的冗余。从(13)式中可以看出，接收数据矩阵C和Q都包含有垂直方向和水平方向的阵元信息，相比于文献[10]的划分方式更加有效。虽然按照本文的子阵划分方式会带来角度配对的额外过程，但是可以使得传播算子算法可以充分利用阵元输出数据，联合估计俯仰角和方位角的信息。

2.2 求解旋转矩阵

首先对xoz平面内的L型阵列的阵元数据进行分析，将Am分块表示如下

(14)

(14)式中:Am1∈CK×K是一个非奇异矩阵；Am2∈C(2M-1-K)×K可由Am1线性表示，即存在一个K×(2M-1-K)维度的传播算子矩阵P满足

PHAm1=Am2

(15)

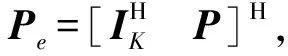
PeAm1=Am

(16)

取Pe的前M行和后M行分别构成矩阵Px和Pxz，定义矩阵Px1和Px2分别为矩阵Px的后M-1行和前M-1行，考虑到均匀线性阵列的旋转不变性，则有

Px1Am1Φx=Px2Am1

(17)

(17)式中，Φx=diag[e-j2πsinθ1cosφ1d/λ,e-j2πsinθ2cosφ2d/λ,…,e-j2πsinθK-1cosφK-1d/λ,e-j2πsinθKcosφKd/λ]，那么由(17)式推出

(18)

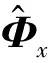
(19)

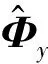
2.3 角度配对

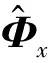
(20)

s.t. ∀Ξi,j={0,1},

(21)

(21)式中：‖·‖F和‖·‖1分别代表取矩阵的Frobenius范数和1范数；(·)i·，(·)·j和(·)i,j分别代表取矩阵的第i行、第j列和位于第i行与第j列交叉处的元素。通过求出置换矩阵获得和的配对关系，并将二者的平均值作为新的估计值

(22)

(23)

则俯仰角和方位角的估计值分别为

(24)

(25)

2.4 算法步骤总结

算法主要步骤总结如下。

步骤1对接收数据进行重排整理，并构造2个新的数据接收矩阵C和Q；

步骤2计算C的协方差矩阵，划分协方差矩阵并由(9)式得到扩展传播算子Pe；

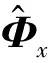
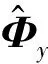
步骤5通过(23)式得到3个配对后的旋转矩阵关系式；

步骤6计算(24)式和(25)式，获得估计的俯仰角和方位角。

2.5 算法复杂度分析

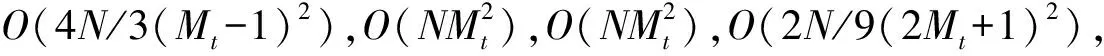
表1为取N=200时，复杂度随Mt变化的情况。可以看出,本文所提算法比其他几种算法的计算量要小。

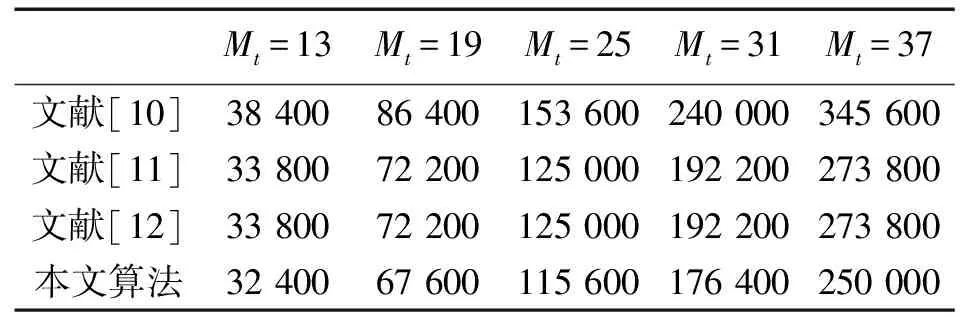
表1 算法复杂度比较Tab.1 Comparison of algorithm complexity

3 实验仿真及分析

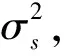
(26)

3.1 仿真1

图2a和图2b分别展示了本文算法在信噪比为5 dB和15 dB时对方位角和俯仰角估计结果的散布图，用以说明对3个目标源信号的分辨情况。图2中的3个不同位置的散点分布表示对3个不同信号源角度估计值的分布情况。仿真实验中设置3个目标源的方位角和俯仰角分别为(50°，80°),(75°，20°)和(30°，60°)，蒙特卡洛仿真次数为500次，快拍数、每个子阵的阵元数和信源数分别为N=200，M=9，K=3。

从图2a和图2b中可以看出，在信噪比为5 dB和15 dB的实验环境下，3个信号源的方位角和俯仰角的估计值分布都比较集中，且比较接近于实验设置的真实值，没有出现偏离真实值较大的异常值。说明本文算法可以比较稳定准确地分辨出各个信号的方位角和俯仰角，验证了本文算法的有效性，同时也说明对于不同的信噪比有较好的鲁棒性。对比图2a和图2b可以看出，在高信噪比的环境下，角度估计值更加接近真实值，误差更小。

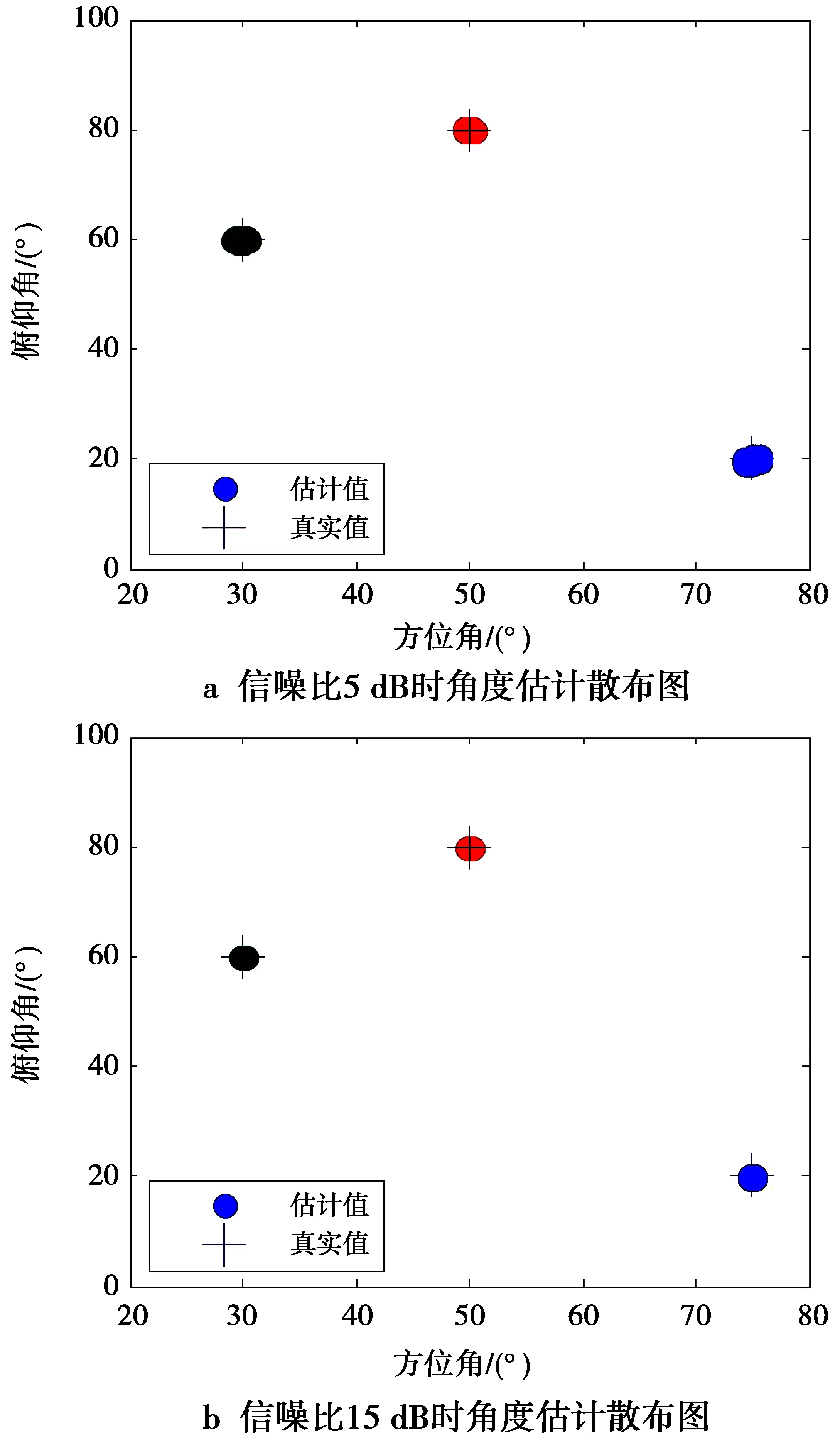
图2 角度估计散布图Fig.2 Scatter gram of DOA estimation

3.2 仿真2

图3展示了在相同环境条件下，随着信噪比变化时文献[10]算法、文献[11]算法、文献[12]算法、本文提出的算法以及克拉美罗界(CRB)的性能比较。采用角度估计的均方误差来衡量算法的性能表现。实验中设置(50°，70°)和(70°，85°)2个目标信号源，阵元总数都设置为25，快拍数为200，蒙特卡洛仿真次数为500次，信噪比的变化为0～30 dB。

从图3中可以看出，无论是方位角、俯仰角还是联合角度误差估计，本文算法的RMSE都是几种方法中最低的，更接近于CRB，整体上来看优于其他几种方法。这不仅仅是因为双L型阵列结构有着良好的性能，更是由于本文算法充分利用了阵元的接收数据信息，避免了阵列孔径损失，从而获得了更高的角度估计精度。

文献[10]的方法在俯仰角和联合角度估计时可以获得比文献[11]和文献[12]更小的估计误差，而其方位角估计性能比较差。从图3a中可以看出,文献[11]的方位角估计误差要比文献[10]和文献[12]中方法的误差要小，这是由于文献[11]采用双平行阵列，在水平面具有更大的阵列孔径，在对方位角估计时有更大的优势。从图3b和图3c中可以看出，文献[12]在俯仰角估计和联合角度估计时的性能优于文献[11]，说明其对于文献[11]的改进是有效果的。

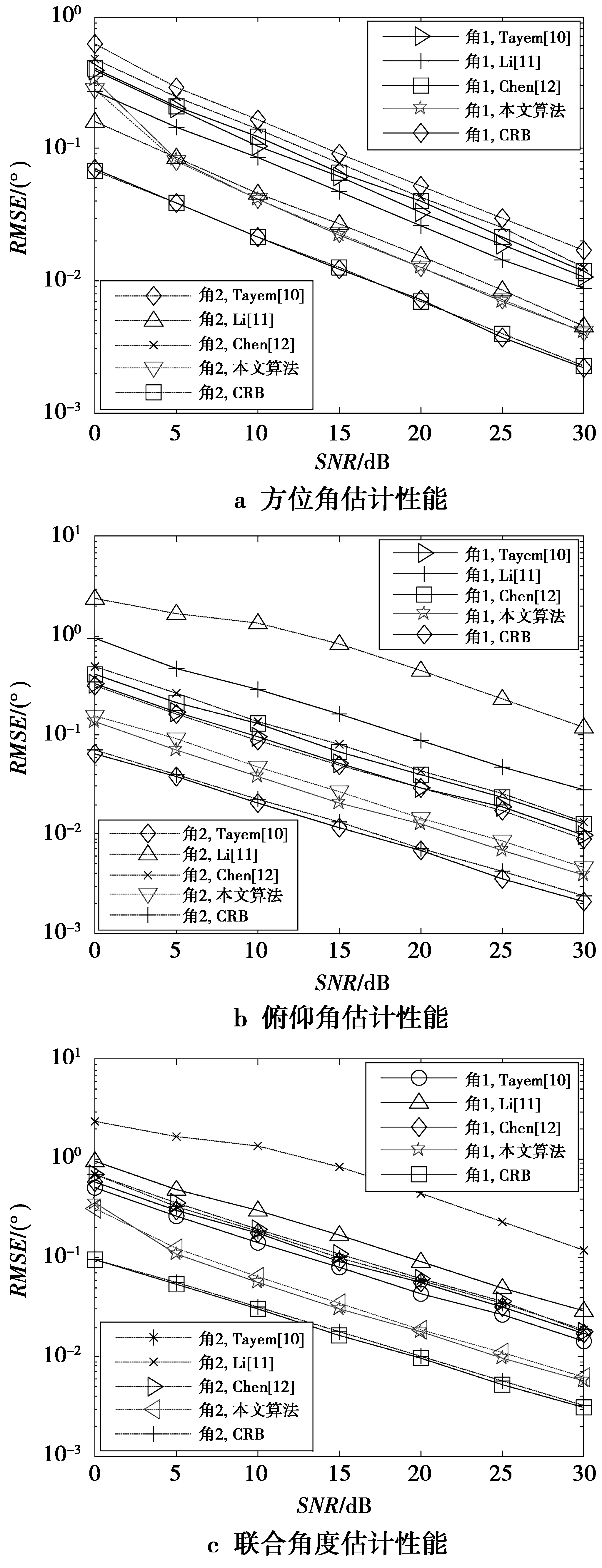
图3 不同信噪比下角度估计均方误差图Fig.3 RMSE performance of DOA estimation at different SNR

3.3 仿真3

图4为RMSE的三维mesh图，展示了本文算法和其他算法在不同方位角和俯仰角组合下的联合均方误差。仿真实验中假设有一个信号源入射到天线阵列上，信噪比SNR=10 dB,其他条件与仿真2中相同。入射信号源的方位角和俯仰角均在10°～80°，以2°的步长变化。

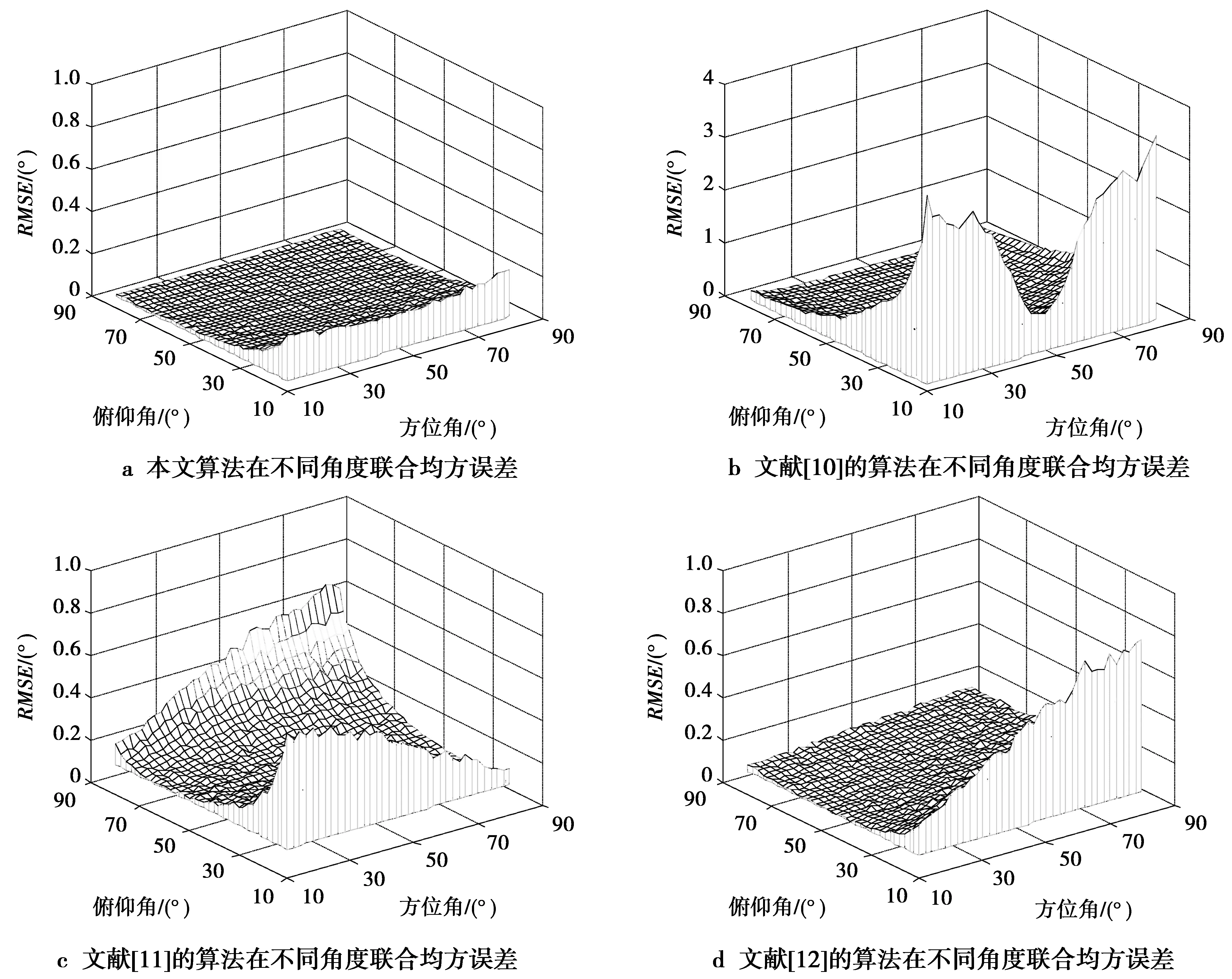
图4 不同角度组合下均方误差的三维mest图Fig.4 Three dimensional mest diagram of RMSE performance at different angles

从图4a可以看出，对于不同的二维角度组合，本文给出算法的均方误差曲线比较平滑,并且误差比较小。这是由于双L型阵列在结构上有对称性，在水平面和垂直面内具有相同的阵列孔径。本文提出的划分子阵的方式也充分利用了这种特点，每个子阵都可以获取水平面和垂直面的信源信息，所以对于给定的俯仰角和方位角的角度组合，其性能是近似平均的。

文献[10]虽然也采用了双L型阵列结构，但是其划分子阵的方式不能充分利用其结构特点，构造的信号协方差矩阵存在冗余数据，利用传播算子方法求解旋转矩阵时存在阵元信息丢失问题，所以其算法性能表现不如本文。从图4b可以看出，由于在估计俯仰角时只是利用了z轴方向的阵元信息，所以当俯仰角越接近于0度时，即信号源接近于垂直入射，误差越大。而在方位角较小和较大时，误差会变大。出现这种现象是因为在方位角较小和较大时会出现阵元信息损失问题。

文献[11]采用的是双平行阵列，在图4c中可以看出，在俯仰角和方位角都较小或者都较大时误差都会变大，这是由于在这2种情况下信号在天线阵列上产生的相移接近于0。

从图4d中可以看出，由于文献[12]采用的是三平行阵列，相比于双平行阵列增加了垂直方向的阵元信息，所以仅在俯仰角较小且方位角较大时估计误差増大，比文献[11]的估计效果更好。

4 结束语

本文针对双L型结构的阵列天线角度估计问题进行了研究。通过对子阵接收数据的重新排列和组合，使所有的阵元信息得到有效利用。构造的信号协方差矩阵不存在冗余数据，降低了求解二阶统计特性时的计算代价。结合均匀线性阵列的旋转不变性，将平行线阵中采用的改进传播算子的二维DOA估计算法扩展到双L型阵列中，并通过求最小范数的方法对角度信息配对，配对方法简单。该算法无需对接收数据进行特征值或奇异值分解，因此，具有较低的计算复杂度。计算机仿真证明该算法的估计精度要高于其他一些经典文献的算法，具有良好的估计性能。在无线电电子侦测中精确测定辐射源来向、智能天线中测定信号来向和测定无线电台方位等场景中具有一定的应用价值。

参考文献：

[1] HARABI F, GHARSALLAH A, MARCOS S. Three-dimensional antennas array for the estimation of direction of arrival [J]. IET Microwaves, Antennas & Propagation, 2009, 3(5):843-849.

[2] WEN Fei, WAN Qun, FAN Rong, et al. Improved MUSIC algorithm for multiple noncoherent subarray [J]. IEEE Signal Processing Letters, 2014, 21(5): 527 -530.

[3] AHMED A, KHAN M F, TUFAIL M. Multiple invariance cumulant ESPRIT for DOA estimation[C]// International Conference on Robotics and Emerging Allied Technologies in Engineering. Islamabad, Pakistan: IEEE, 2014:157-159.

[4] LIU Ding, LIANG Junli. L-shaped array-based 2-D DOA estimation using parallel factor analysis[C]// Intelligent Control and Automation. Jinan, China: IEEE, 2010: 6949-6952.

[5] LIU T H, MENDEL J M. Azimuth and elevation direction finding using arbitrary array geometries [J]. IEEE Transactions on Signal Processing, 1998, 46(7):2061-2065.

[6] 夏莘媛, 高鹏飞, 戴静. 基于压缩感知的智能天线DOA估计算法[J]. 重庆邮电大学学报:自然科学版, 2016, 28(5):701-706.

XIA Xinyuan, GAO Pengfei, DAI Jing. DOA estimation algorithms in smart antennas based on compressed sensing [J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2016, 28(5):701-706.

[7] 符博博, 郑娜娥, 胡捍英.单基地MIMO雷达中基于改进传播算子的二维DOA估计算法[J]. 信号处理, 2016, 32(4):438-443.

FU Bobo, ZHENG Na’e, HU Hanying. A Two- dimensional DOA estimation algorithm based on improved propagator for monostatic MIMO radar [J].Signal Processing, 2016, 32(4): 438-443.

[8] MARCOS S, MARSAL A, BENIDIR M. The propagator method for source bearing estimation [J]. Signal Processing, 1995, 42(2):121-138.

[9] WU Yuntao, LIAO Guisheng, SO H C. A fast algorithm for 2-D direction-of-arrival estimation [J]. Signal Processing, 2003, 83(8):1827-1831.

[10] TAYEM N, KWON H M. L-shape 2-dimensional arrival angle estimation with propagator method [J]. IEEE Transactions on Antennas & Propagation, 2005, 53(5):1622-1630.

[11] LI Jianfeng, ZHANG Xiaofei, CHEN Han. Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method [J]. Signal Processing, 2012, 92 (12):3032-3038

[12] CHEN Hua, HOU Chunping, WANG Qing, et al. Improved azimuth/elevation angle estimation algorithm for three-parallel uniform linear arrays [J]. IEEE Antennas & Wireless Propagation Letters, 2015(14):329-332.

[13] LUO Jun, ZHANG Guoping, YU Kegen. An automatically paired two-dimensional direction-of- arrival estimation method for two parallel uniform linear arrays [J]. AEU- International Journal of Electronics and Communications, 2017(72):46-51.

[14] DONG Yangyang, DONG Chunxi, XU Jin, et al. Computationally efficient 2-D DOA estimation for L-shaped array with automatic pairing [J]. IEEE Antennas & Wireless Propagation Letters, 2016(15):1.

[15] TAYEM N, MAJEED K, HUSSAIN A A. Two- dimensional DOA estimation using cross-correla- tion matrix with L-Shaped array [J]. IEEE Antennas & Wireless Propagation Letters, 2016(15):1077-1080.

[16] WANG Qing, YANG Hang, CHEN Hua, et al. A low-complexity method for two-dimensional direction-of-arrival estimation using an L-Shaped array [J]. Sensors, 2017,17(1):190-191.