基于ESPRIT的ULA波达方向估计改进算法
2013-10-15宋雪松姚桂锦
宋雪松, 姚桂锦, 徐 洄
(1. 吉林大学 通信工程学院, 长春 130012; 2. 吉林省高速公路管理局, 长春 130022)
0 引 言
波达方向(DOA: Direction-of-Arrival)估计是阵列信号处理的重要研究内容和持续研究热点之一。从20世纪70年代末开始, 在DOA估计算法方面涌现了大量的研究成果[1,2], 其中特征子空间类算法已发展成最常用的一类算法, 其代表是MUSIC算法[3]和ESPRIT算法[4], 并在这两种算法基础上人们也提出了一些改进算法[5-7]。但特征子空间类算法面临的一个普遍问题是: 由于阵列接收数据协方差矩阵会出现降秩问题, 该类算法无法对相干信源进行DOA估计。空间平滑类算法[8-11]通过对阵列接收数据划分子阵并对子阵协方差矩阵求平均值, 达到解相干和恢复阵列数据协方差矩阵原秩, 但该类算法以牺牲传感器阵列孔径和降低估计来波信号的数目为代价。最近, 文献[12]提出的CC-ESPRIT(Cross ESPRIT)算法能同时处理相干和非相干信号情况, 但相干信号角度间隔较小时, 算法性能不稳定; 文献[13]和文献[14]虽然能估计角度间隔较小的相干信源, 但低信噪比的估计效果不理想。笔者采用MMUSIC(Modified MUSIC)算法原理, 对阵列接收数据矩阵的自相关和互相关信息进行变换, 并且重新构造数据矩阵, 最后结合TLS-ESPRIT(Total Least-Squares ESPRIT)算法提出了能同时适应相干和非相干信号情况的波达方向估计的改进ESPRIT算法(IM-ESPRIT: Improved ESPRIT), 在较低信噪比和相干信源角度间隔较小等约束条件下, 对IM-ESPRIT算法进行了理论分析和数值仿真。
1 IM-ESPRIT算法的基本原理
1.1 MMUSIC算法
设有一M个各向同性阵元的均匀线阵(ULA: Uniform Linear Array), 阵元间距为d, 与线阵轴线法线呈θi(i=1,2,…,N)角度上有N个窄带信号源si(t), 这里约定N X(k)=AS(k)+N(k) (1) 其中X(k)=[x1(k),x2(k),…,xM(k)]T,S(k)=[s1(k),s2(k),…,sN(k)]T和N(k)=[n1(k),n2(k),…,nM(k)]T分别为阵列接收数据矢量、 信号矢量和阵元噪声矢量。其中xj(k)(j=1,…,M)为第j个阵元传感器输出,nj(k)为第j个阵元传感器的噪声, 这里假定nj(k)是与各信号源不相关且相互独立的零均值、 方差为σ2的白噪声,A=[a(θ1),a(θ2),…,a(θN)]为阵列流型矩阵, 其中a(θi)=[1,e-jΦi,e-j2Φi,…,e-j(M-1)Φi]T,Φi=2πdsin(θi)/λ, (·)T表示转置。 阵列接收数据协方差矩阵为 RXX=E[X(k)X(k)H]=ARSAH+σ2IM (2) 其中RS=E[S(k)SH(k)]为信号协方差矩阵,IM为M×M阶单位矩阵。对于相关信号源DOA估计, 为恢复接收阵列数据协方差的秩, 实现解相干, 这里取变换矩阵 (3) 并定义 Y(k)=JMX*(k) (4) 式(4)中,X*(k)是X(k)的复共轭矩阵, 由于JMJM=IM,Y(k)协方差矩阵表示为 (5) 令 (6) 由式(6)分析可看出, 矩阵R1只涉及到数据X(k)和Y(k)的自相关矩阵, 而没有利用X(k)与Y(k)互相关特性, 因此数据信息没有充分利用, 有损失, 会导致算法性能下降。为进一步提高针对相干信号的DOA估计的分辨率性能, 笔者提出利用X(k)和Y(k)的自相关矩阵和互相关矩阵, 再通过重构相关的矩阵, 进而对相干信号进行DOA估计的一种算法。 重新定义阵列接收数据自相关矩阵为 RXX=E[X(k)X(k+1)H] (7) 由于噪声之间相互独立, 这里N(k)和N(k+1)是不相关的, 式(7)可起到降噪作用。对Y(k)的自相关矩阵也是同式(7)定义。 X(k)和Y(k)的互协方差矩阵为 RXY=E[X(k)YH(k)] (8) 定义 (9) 则重构矩阵定义为 (10) 由式(9)和式(10)可以看出, 笔者将MMUSIC解相干算法的思想应用于阵列接收数据的自相关、 互相关矩阵变换上。即通过利用变换矩阵对阵列接收数据的自相关、 互相关矩阵进行变换, 再相加, 对数据噪声起到平均作用, 达到在估计角度间隔较小的条件下实现相干信源DOA估计。而CC-ESPRIT算法[12]仅是直接运用阵列接收数据的自相关、互相关矩阵重设构造矩阵。 (11) 其中矩阵Λ中各特征值是按照从大到小降序排列,E是与其特征值对应的特征向量矩阵, 表示如下 (12) 式(12)中分块矩阵Eij(i=1,2;j=1,2)都是N×N维, 则有 (13) 对Ψ进行特征值分解, 得到特征值λi=ejΦi, 进而估计信号的波达方向θi(i=1,…,M)。 上述算法定义为IM-ESPRIT算法, 通过分析, 该算法有如下特点: 1) 算法通过变换矩阵对阵列接收数据变换后, 利用阵列接收数据及其变换矩阵的自相关矩阵和互相关矩阵, 实现对相干信号的解相干过程。 2) 由于充分利用了阵列接收数据及其变换矩阵的自相关、 互相关信息, 因此, 能估计角度间隔较小的相干信源, 提高了算法的角度估计分辨能力。 算法流程如下: 1) 利用式(3)~式(9)计算自相关矩阵R1、R2和互相关矩阵R3, 重构协方差矩阵R; 2) 对协方差矩阵R进行奇异值分解, 已知信源数N, 确定信号子空间US; 4) 根据式(12)将矩阵E划分为4个相同维数的子矩阵, 利用式(13)求得矩阵Ψ, 对矩阵Ψ进行特征值分解, 得到特征值λi, 然后求解待测信号的波达方向。 利用笔者提出的IM-ESPRIT算法对一维均匀线阵(ULA)开展DOA估计, 并与CC-ESPRIT算法估计结果进行对比与性能分析。相关参数如下: 阵元数M=10, 信源数为N=3, 来波方向分别为: 10°、30°和65°。前两个信号相干, 与第3个信号不相干。快拍数(采样数)为K=2 000, 阵元间距为半波长, 各阵元噪声均为方差为1的高斯白噪声。 1) 不同信噪比条件下, IM-ESPRIT算法和CC-ESPRIT算法仿真结果对比分析。 图1 IM-ESPRIT算法和CC-ESPRIT算法DOA估计分辨率比较 图1为IM-ESPRIT算法和CC-ESPRIT算法DOA估计分辨率比较。由图1可以看出, IM-ESPRIT算法和CC-ESPRIT算法都能同时处理相干和非相干信号源情况, 但在相同信噪比条件下, IM-ESPRIT算法的估计精度比CC-ESPRIT稍高。 2) IM-ESPRIT算法与CC-ESPRIT算法相干信号角度估计分辨率对比与分析。 3个信号源波达方向分别为: 10°、13°和60°, 前两个信号源为相干源, 但方向角度间隔明显变小, 其他仿真参数同1)。表1为相干信号的CC-ESPRIT算法仿真结果, 表2为相干信号的IM-ESPRIT算法仿真结果。 表1 相干信号的CC-ESPRIT算法仿真结果 注:X表示不能估计波达方向 表2 相干信号的IM-ESPRIT算法仿真结果 注:X表示不能估计波达方向 图2 IM-ESPRIT算法和CC-ESPRIT算法的DOA估计均方根误差 由表1和2分析可看出, 在两个相干信号源的角度间隔较小的条件下, 无论针对高、 低信噪比, CC-ESPRIT算法都不能给出相干信号波达方向, 算法失效。IM-ESPRIT算法只是在信噪比为-5 dB或更低时, 无法给出两个相干信号源波达方向, 同CC-ESPRIT算法仿真结果比较, 对相干信号源角度估计的分辨率性能明显要好, 但结果同时也表明, 随着相干信号源的角度间隔逐渐变小时, IM-ESPRIT算法也需要相应提高接收数据信噪比。 3) 不同信噪比条件下, IM-ESPRIT算法与CC-ESPRIT算法角度估计均方误差对比与分析。 图2给出了IM-ESPRIT算法和CC-ESPRIT算法均方误差随信噪比变化的曲线。由图2可看出, 随着信噪比的改善, 两种算法的均方根误差都变小, 但IM-ESPRIT算法均方误差明显比CC-ESPRIT算法小, 这表明在相同信噪比情况下, IM-ESPRIT算法的估计精度较高。 笔者采用MMUSIC算法思想, 通过引入变换矩阵, 在考虑到阵列接收数据及其相应变换矩阵的自相关矩阵和互相关矩阵后, 提出了能同时适应相干和非相干信号情况的波达方向估计的IM-ESPRIT算法。该算法理论和数值仿真表明, 在较低信噪比和相干信源角度间隔较小等约束条件下, 同常规CC-ESPRIT算法比较, 具有较好的分辨能力和估计精度, 数值仿真验证了IM-ESPRIT算法的有效性和稳定性。对阵列信号处理中相干信源DOA估计的研究具有一定参考意义。 参考文献: [1]王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法 [M]. 北京: 清华大学出版社, 2004. WANG Yong-liang, CHEN Hui, PENG Ying-ning, et al. Theory of Spatial Spectrum Estimation and Algorithm [M]. Beijing: Tsinghua University Press, 2004. [2]HOLZMAN E. Introduction to Direction-of-Arrival Estimation [J]. Antennas and Propagation Magazine, 2011, 53(1): 110-111. [3]SCHMIDT R. Multiple Emitter Location and Signal Parameter Estimation [J]. IEEE Trans on Antennas and Propagation, March 1986, 34(3): 276-280. [4]ROY R, KAILATH T. ESPRIT-Estimation of Signal Parameters via Rotational Invariance Techniques [J]. IEEE Trans on ASSP, 1989, 37(7): 984-995. [5]BOURI, MOHAMED. A Novel Fast High Resolution MUSIC Algorithm [J]. Signal Processing Systems, 2012, 26(6): 237-242. [6]LI Bo. Estimation for Signal’s DOA by MMUSIC Algorithm [J]. Journal of Computational Information Systems, 2011, 15(7): 5461-5468. [7]FERREIRA T, NETTO S, DINIZ P. Direction-of-Arrival Estimation Using a Low-Complexity Covariance-Based Approach [J]. IEEE Transaction on Aerospace and Electronic Systems, 2012, 48(3): 1924-1934. [8]PILLAI S U, KWON B H. Forward/Backward Spatial Smoothing Techniques for Coherent Signals Identification [J]. IEEE Trans on Acoustic Speech and Signal Processing, 1989, 37(1): 8-15. [9]刘宁, 刘玉生. 相干信号的空间谱估计算法研究 [J]. 计算机仿真, 2012, 29(11): 218-222. LIU Ning, LIU Yu-sheng. Research on Algorithm for Spatial Spectrum Estimation of Coherent Signals[J]. Computer Simulation, 2012, 29(11): 218-222. [10]姚林宏, 高鹰, 石宇, 等. 冲击噪声背景下的虚拟空间平滑算法 [J]. 吉林大学学报: 信息科学版, 2011, 29(1): 47-50. YAO Lin-hong, GAO Ying, SHI Yu, et al. Virtual Spatial Smoothing Algorithm in Presence of Impulsive Noise [J]. Journal of Jilin University: Information Science Edition, 2011, 29(1): 47-50. [11]DAI J, YE Z. Spatial Smoothing for Direction of Arrival Estimation of Coherent Signals in the Presence of Unknown Mutual Coupling [J]. IET Signal Processing, 2011, 5(4): 390-396. [12]曾明, 徐建成, 蔡会甫. 估计相干与非相干信源的ESPRIT新方法 [J]. 信息安全与通信保密, 2010(5): 58-60. ZENG Ming, XU Jian-cheng, CAI Hui-fu. A Novel ESPRIT Method for Estimating Non-Coherent and Coherent Source [J]. Information Security and Communications Privacy, 2010(5): 58-60. [13]姚林宏, 高鹰, 石宇, 等. 基于均匀线阵的改进MUSIC算法 [J]. 吉林大学学报: 信息科学版, 2010, 28(6): 558-662. YAO Lin-hong, GAO Ying, SHI Yu, et al. Research on Improved Algorithm of MMUSIC Based on ULA [J]. Journal of Jilin University: Information Science Edition, 2010, 28(6): 558-662. [14]洪伟. 一种对修正MUSIC算法的改进测向方法 [J]. 舰船电子对抗, 2011, 34(3): 71-73. HONG Wei. An Improved Direction-Finding Method of Modified MUSIC Algorithm [J]. Shipboard Electronic Countermeasure, 2011, 34(3): 71-73. [15]KUN DU D. Modified MUSIC Algorithm for Estimation DOA of Signal [J]. Signal Processing, 1996, 48(1): 85-89.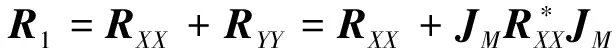
1.2 IM-ESPRIT算法


2 IM-ESPRIT算法实现流程

3 仿真实验




4 结 语
