卫星网络中基于蚁群优化的概率路由算法

戴翠琴，尹小盼

(重庆邮电大学 移动通信技术重点实验室，重庆 400065)

0 引 言

与地面通信网络相比，卫星通信网络具有广覆盖、大容量、远距离传输等优点，能够满足灵活、动态的空间网络配置需求[1]。但是，由于卫星节点围绕地球周期性的运动特性，使得网络拓扑结构动态变化、星间链路(inter-satellite link, ISL)频繁切换、链路长度和通断关系随时间动态变化，对空间信息传输的有效性和可靠性造成了严重的影响。同时，考虑到星上资源有限、负载分布不均匀等因素，如何设计高效、可靠、灵活的卫星网络路由算法日益成为研究者们关注的热点问题[2-3]。

目前，按照路由算法能否根据网络拓扑的变化及时更新路由表，可将卫星网络中的路由算法大致分为两类：静态路由算法[4]和动态路由算法[5-8]。其中，文献[4]将低轨卫星网络(low earth orbit, LEO)模拟成有限状态自动机，将LEO卫星网络的动态链路分配问题转换为静态网络拓扑结构中的固定链路分配和路由优化问题。但是，由于静态路由机制不能根据网络流量和拓扑结构的变化来调整自身的路由表，也就无法适应星间链路的动态变化。相比之下，动态路由算法充分考虑了网络当前的实时状态信息，使得路由选择能够更好地适应网络流量、拓扑结构的变化，能够改善网络整体性能。文献[5]在LEO卫星网络中提出了一种基于分布式负载感知的动态路由算法，采用一种逐跳机制来分割流量负载，以缓解极区附近发生的拥塞问题。文献[6]针对最短路径问题，提出一种动态虚拟拓扑路由(dynamic virtual topology routing, DVTR)算法。文献[7]针对如何延长卫星使用寿命的问题，提出了一种能量高效的路由算法。文献[8]提出了一种基于代理分组交换的动态路由算法，改善了网络吞吐性能。文献[9]考虑了卫星网络中的传输业务需求，提出了一种基于多业务传输优化的动态路由算法，但未考虑网络吞吐量和链路利用率。因此，现有卫星网络中的动态路由算法主要针对某个单一的特定问题进行优化，没有能够同时兼顾网络拓扑动态变化和链路频繁切换对网络性能造成的影响。因此，以上研究结果若直接应用到卫星时变网络中，将产生端到端时延增大、星上资源利用率低等问题。

蚁群优化(ant colony optimization, ACO)，是一种用来寻找最优路径的机率型算法，最早由Marco Dorigo提出[10]，来源于蚂蚁在寻找食物过程中发现路径的行为。ACO具有自适应性和鲁棒性的优点，能够通过正反馈、分布式协作来寻找最优径。因此，近来已有少量文献将ACO运用在卫星网络中的路由路径计算中，使之能够适应卫星网络拓扑动态变化的同时平衡网络负载，进而减少或避免发生链路拥塞[11-15]。其中，文献[11]通过改善传统蚁群优化，利用虚拟拓扑解决了卫星网络中拓扑快速变化的问题，虽然提高了蚁群优化的收敛时间，但是没有解决链路易发生拥塞的问题。文献[12]中提出一种基于改进蚁群优化的自适应路由优化算法(improved ant colony optimization, IACO)，改善了ACO算法易导致ISL发生拥塞和路由收敛时间慢的缺点。文献[13]提出一种跨层设计和基于ACO的负载均衡路由算法(cross-layer design and ant-colony optimization based load-balancing routing algorithm, CAL-LSN)，其利用物理层信息作出路由决定，采用多目标优化模型实现负载均衡。文献[14]运用ACO的启发式方法提出了一种路由优化算法，使得寻找到的最优路径具有最大吞吐量。文献[15]结合概率路由协议(probabilistic routing protocol using history of encounters and transitivity, ProPHET)的概率度量标准和ACO算法，提出了一种基于蚁群优化的ProPHET改进方案，提高信息传输率的同时降低了网络成本。以上已有的基于ACO的卫星网络路由算法主要针对收敛时间进行了优化，均没有考虑到卫星网络中数据包的传输时延和ISL利用率问题。同时，由于卫星网络拓扑的动态变化，当多个包需要传输时，一个连通时间片内不能完全将数据包完全转发到目的节点，需等待下一个连通时间片，这将会产生多个节点向同一节点发送包，进而造成链路使用冲突、系统丢包率增大以及传输包时延增大等问题。

针对以上问题，本文综合考虑卫星网络中时延带宽和链路容量2个因素对传输路径选择的影响，提出一种基于蚁群优化的概率路由算法(ant colony optimization based probabilistic routing algorithm, ACO-PRA)。首先，结合卫星网络拓扑动态时变特性，将链路容量和星间链路距离2个性能因素引入到ACO节点选择概率函数中，建立最小化时延目标函数；然后，根据节点概率函数选择下一跳节点，最终找到一条最佳信号传输路径。仿真结果表明，相比DVTR[6]算法和IACO[12]算法,ACO-PRA算法不仅在网络吞吐量上有较大提高，而且在平均时延性能上也有明显的改善。

1 系统模型

1.1 卫星网络模型

以LEO卫星为例，建立LEO卫星网络模型如图1a所示。该系统由若干颗LEO卫星组成，运用分时方法将卫星运转周期T划分为n个时间片Δt，如图1b所示。在每个时间片内，卫星网络可以看做一个静态的无向图G=(V,E)。其中，V=N×M表示卫星星座中共有分布于N条卫星轨道，每条轨道有M颗卫星，任意时间片内可以连通的卫星节点集合，E表示卫星间的星间链路ISL。星间链路可分为两类：轨道内的星间链路(Intra-plane ISL)和轨道间的星间链路(Inter-plane ISL)。同一轨道内的卫星的相对位置变化比较小，所以链路可以长期保持连通；而不同轨道内的卫星之间的距离和视角动态变化，ISL很难长时间保持，经常会发生临时性的中断。设每个时间片Δt取得足够小，星际链路长度和连通关系的改变仅在每个Δt的开始时刻t0,t1,…或tn发生。因此，动态的卫星网络拓扑被离散化为一系列静态网络拓扑连通图。

图1 系统模型Fig.1 System model

1.2 星间可见性

由于卫星围绕地球周期性地运转，任意2颗卫星vi,vj之间的可见性也随着卫星运行时间的变化而改变，造成星间通信链路频繁切换，导致传统的蚁群算法计算得到的结果不能保证是最优解。因此，分析星间可见性、获得星间连接及距离信息是进行卫星网络中动态路由算法设计的必要环节。

星间可见性几何模型如图2所示，设地球半径为R，卫星轨道高度为r，大气层高度为h，任意2颗卫星vi与vj之间的通信链路距离为Lij。从地球遮挡和大气影响考虑，星—星可见性条件如(1)式所示

(1)

图2 星间可见性的几何模型Fig.2 Geometry model of inter satellite visibility

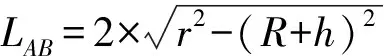
2 ACO-PRA算法总体描述

2.1 问题描述

卫星网络拓扑呈周期可预测性、时刻动态变化，这是不同于传统地面网络的主要特点。传统蚁群算法，通过概率函数选择下一跳节点，具有平衡网络负载与避免网络发生拥塞等优点。但是，LEO卫星上的资源有限，一旦发射硬件设施很难改善；同时，当每个节点都选择最优节点作为下一跳节点时，容易产生星间链路使用冲突的问题，引起数据包传输时延增大，降低网络性能。因此，地面网络中成熟的蚁群算法不能直接地运用在卫星网络中。

传统蚁群算法的问题分析如图3所示，当信息从源节点S传输到目的节点D时，节点A、节点B与节点C是t1时刻与源节点S相邻的节点集。源节点S发送多个数据包时，在Δt的连通时间片内不能完全将数据包转发到目的节点D。因此，源节点S在t1时刻转发部分数据包到节点A，源节点剩余数据包S剩。随着卫星运行时间的变化，节点E与节点F是ti时刻与节点D相邻的节点。此时，可能会发生源节点S剩、节点E与节点F同时向目的节点D转发数据包。本文假设目的节点D在Δt连通时间片内只能接受某一个节点发送的数据包。由于连通时间有限，在单个时间片内每条ISL只能接收部分数据包，选择合适的ISL以便在最短的时间内将全部的数据包及时地转发到目的节点。

图3 传统蚁群算法的问题分析Fig.3 Problems analysis of traditional ant colony algorithm

因此，传统的蚁群算法应用在卫星时变网络中时，会因星间持续可见的连通时间频繁周期性的变化导致单个时间片无法将数据包全部传输到目的节点的问题。

2.2 建立目标函数

在ACO-PRA算法中，为了保证数据包传输的实时性及避免链路发生拥塞，将链路容量和星间链路距离2个性能因素引入到蚁群算法的节点选择概率函数中，建立最小化时延目标函数。

假设P={v0,v1,…,vd|v0,v1,…,vd∈V}是卫星网络中从源节点v0到目的节点vd中的某一条路径，并用权值W来表示为

∀L(vi,vi+1)∈E

(2)

卫星网络拓扑呈现快速地动态时变性，因此，任意时间片内的拓扑结构各不相同，进而星间链路的连接情况也不同，用(3)式来表述卫星网络中任意2颗卫星vi和vj间的连接情况。

(3)

(3)式中，(Ni,Nj)∈N,(Mi,Mj)∈M。

用矩阵C(t)表示任意2颗卫星vi和vj之间链路上的业务流，如(4)式所示。

(4)

为了更明确地表达卫星网络中从源节点v0到目的节点vd带有权值W的路径P，用(5)式来表示每条链路的成本。

Dlij=ω1Tij+ω2Qij

(5)

在ACO-PRA算法中，从源节点v0到目的节点vd的路径P应满足(6)—(8)式中的约束条件。

min (i,j)∈pRBi,j≥B

(6)

∀Link(i,j)vi,j=vj,i=1,(i,j)∈p

(7)

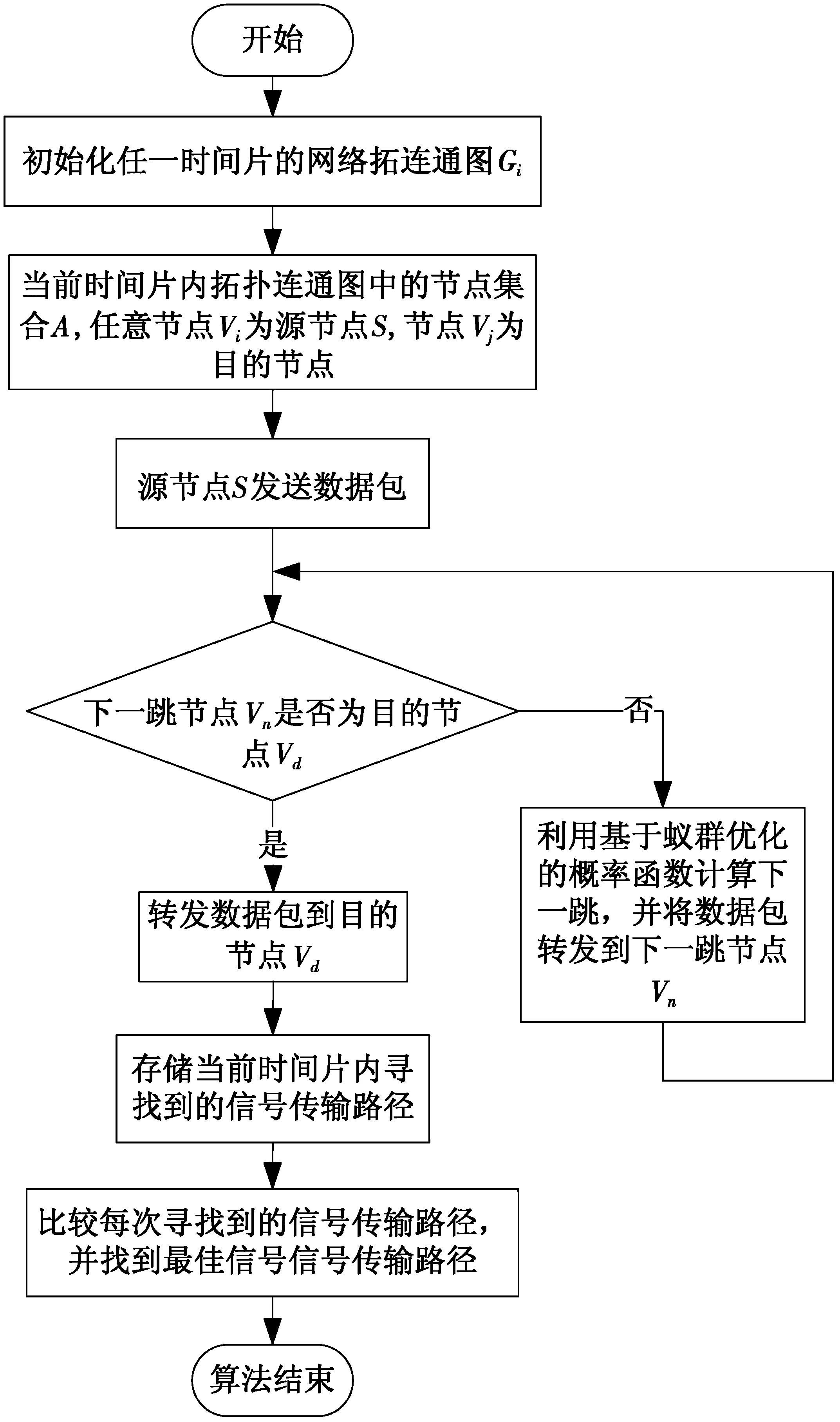
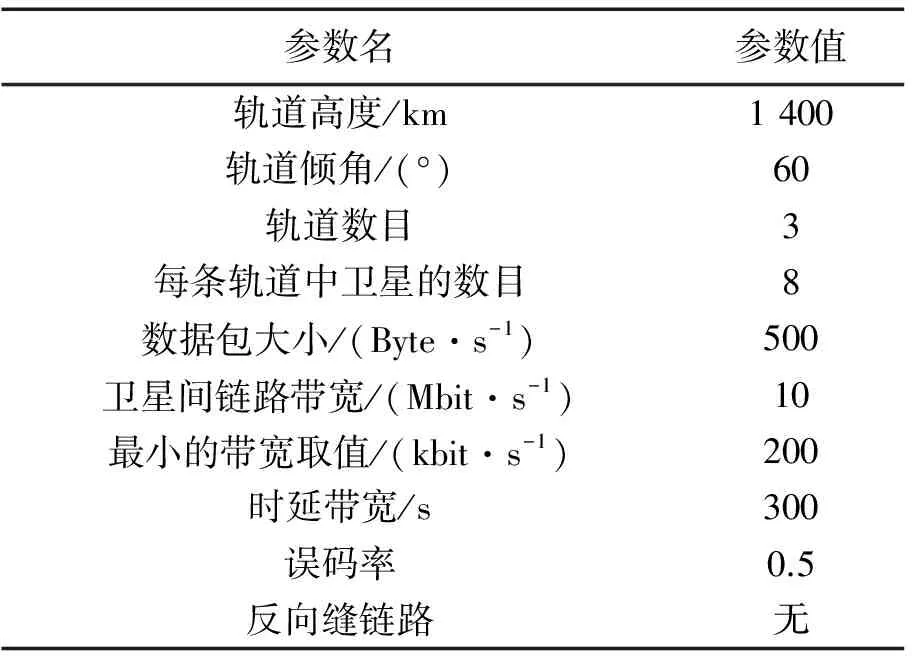
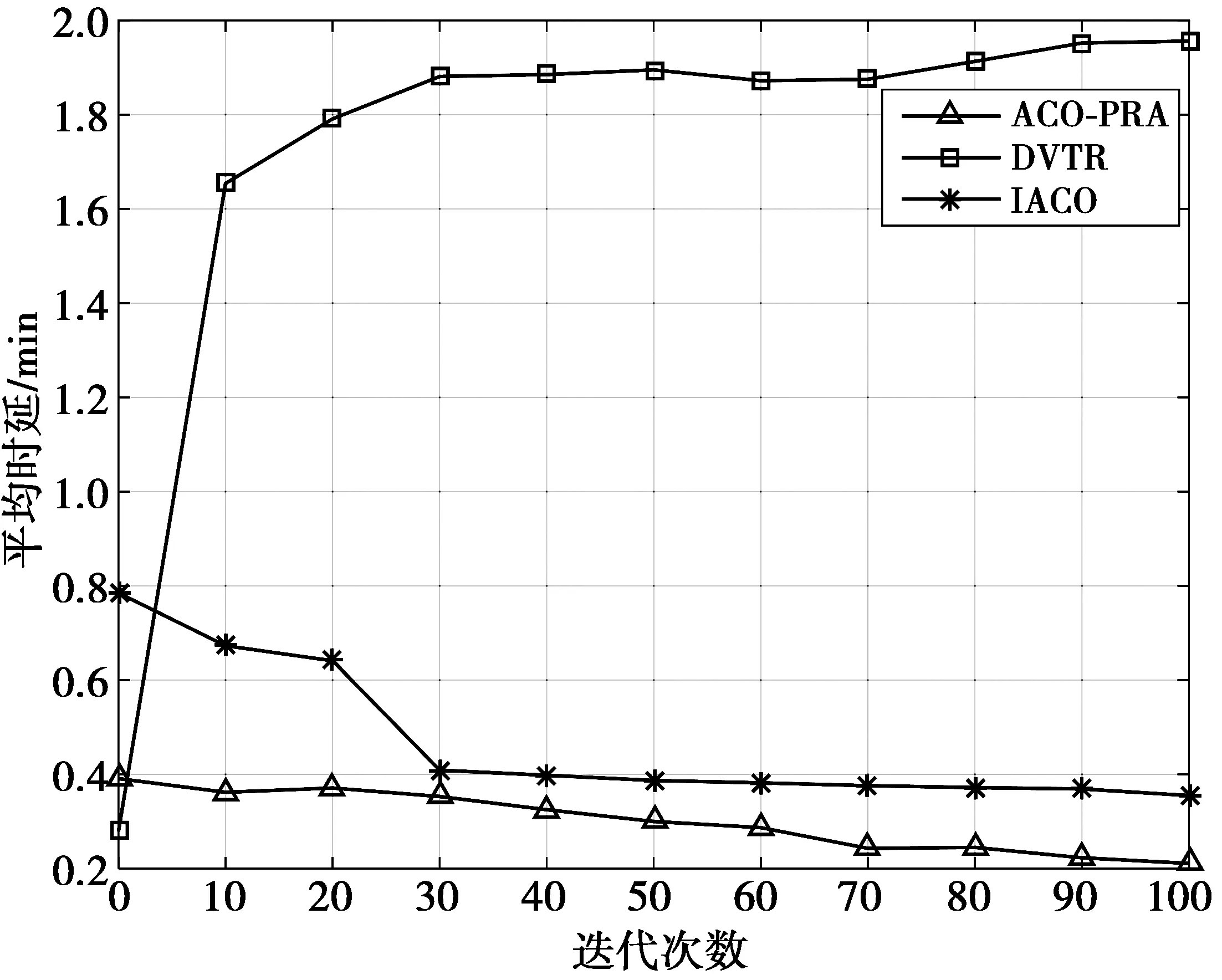
∀ 0

(8)

(6)式中，RBi,j为任意2颗卫星vi和vj间通信链路上的剩余带宽，且RBmax=BW，B为链路传输数据包所需的最小带宽。(6)式用以保证数据包能可靠地进行传输；(7)式表明卫星间相邻可见，能够满足数据传输要求；(8)式表示星间链路上业务流需要满足的约束条件。

2.3 ACO-PRA算法描述

ACO-PRA算法流程如图4所示。下面将在2.2节建立目标函数的优化模型基础上，进一步详细地阐述ACO-PRA算法的具体步骤。算法流程具体如下。

步骤1虚拟化网络拓扑。将卫星运行周期均匀分为若干个时间间隔相等的时间片，根据星间可见性的计算模型分析卫星间的连接及距离信息，从而生成任意时间片的网络拓扑连通图。

步骤2选择相邻节点集。选择任意一时间片内生成的拓扑连通图。任意节点vi为源节点S,vj为目的节点，寻找与S节点相邻的节点集合A。

步骤3判断目的节点。若下一跳节点vn是目的节点，且目的节点vd在与源节点S相邻的节点集合A中，则直接转发数据包，并存储当前时刻寻找到的路由路径；否则，进行步骤4。

步骤4计算概率函数。如果目的节点vd不在与源节点S相邻的节点集合A中，用(9)式计算同时满足时延带宽和链路容量要求的下一跳节点，并转发数据包。之后重复步骤3。

步骤5最佳信号传输路径。遍历所有卫星节点。存储所有数据包到达目的节点vd的路由路径，并比较每条路径，找到最佳信号传输路径。

图4 ACO-PRA算法流程图Fig.4 Flow chart of ACO-PRA algorithm

3 基于概率函数的节点选择

由2.3节描述可知，ACO-PRA算法的基本流程：①综合考虑时延带宽和链路容量，建立最小时延目标函数；②将链路容量和星间距离因子引入到传统ACO算法的节点概率函数中，生成新的节点概率函数；③运用生成的节点概率函数计算下一跳，最终寻找到最佳传输信号的路径。

下面，将重点针对ACO-PRA算法中如何选择下一跳的过程进行详细地阐述。

3.1 基于ACO的节点概率函数

在ACO-PRA算法中，发送数据包的每个卫星节点定义为前向Ant，且前向Ant负责收集节点信息，当前向Ant到达目的节点时，会立即按照原路径返回到源节点，同时Ant会释放一种信息素τ，并用路径上信息素τ浓度的大小来表示路径的远近。结合传统ACO中节点概率函数，ACO-PRA综合考虑了星间链路容量和星间距离2个影响因子。因此，前向节点vi在时刻t选择节点vj作为下一跳节点的概率公式表示为

(9)

(10)

当数据包遍历完所有路径后，节点i和节点j之间链路上的信息素就会更新。因此，在(t+1)时刻节点i和节点j之间链路上的信息素用(11)式来计算

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(11)

(12)

3.2 下一跳节点选择过程

源节点S发送数据包的情况可分为2种：①若下一跳节点为目的节点，则直接将数据包转发；②若不是，数据包将需经过若干个时间片才能转发到目的节点。因而，数据包在传输过程中发生链路选择的问题，即节点vi在[ti,ti+1]时间片内不能将m个数据包完全转发到下一跳节点vm，节点vi就剩余m剩个数据包需等到下一个连通时间片内转发。如图5所示，在某个时间片内会发生3个节点同时向节点D转发数据包。

节点A、节点B与节点C是t时刻与目的点D相邻的节点集。假设链路LAD在时间片[tA,tD]内的连通时间为tAD,链路LBD在时间片[tB,tD]内的连通时间为tBD，链路LCD在时间片[tC,tD]内的连通时间为tCD；当连通时间tAD>tBD>tCD时，选择链路LAD转发数据包；当连通时间tAD=tBD>tCD或者tAD

图5 某一时间片数据包的转发示例Fig.5 Example of forwarding packet in a time slice

4 仿真分析

为了验证ACO-PRA算法性能，本文采用卫星工具包(satellite tool kit，STK)和MATLAB进行了联合仿真。在相同负载的情况下，与LEO卫星网络中典型的路由算法DVTR，IACO在吞吐量、平均时延等性能方面的进行比较分析。

仿真参数设置如表1所示，地球半径为R=6 371 km，LEO卫星星座采用walker卫星星座，24颗卫星均匀分布在3个轨道平面，轨道倾斜角为60°，每颗卫星有2条星间链路、2条星内链路，其中，ρ=0.5[13]。

LEO卫星网络中的吞吐量性能如图6所示。由图6可知，3种算法的吞吐量都随着算法迭代次数的增加而增大，ACO-PRA算法吞吐量性能呈现优势，这是由于在卫星节点高速移动的情况下，造成网络拓扑结构频繁变化，DVTR算法不能及时地更新路由，且路由路径是在地面预先计算后上传给卫星，并没有解决由于网络拓扑结构动态变化而引起的链路频繁切换的重路由问题，从而导致在同一时刻，采用ACO-PRA算法的网络在相同负载情况下收到的数据包数更多。LEO卫星网络中的平均时延性能如图7所示，同一时刻，IACO算法的吞吐量性能总是低于ACO-PRA算法。因为IACO算法并没有考虑链路的剩余带宽；同时，IACO算法总是寻找最优路径，造成最优路径上业务流过重而部分数据包丢失。因此，相比较于ACO-PRA算法，其吞吐量有所降低。

表1 仿真参数设置Tab.1 Simulation parameter settings

图6 LEO卫星网络中的吞吐量性能Fig.6 Throughput performance in LEO satellite networks

由图7可得，随着算法迭代次数的增加，IACO算法和ACO-PRA算法的平均时延性能明显优于DVTR算法。这是因为卫星网络拓扑呈高速动态的变化，ISLs频繁快速切换，当卫星网络中某些星间链路断开或切换，DVTR算法不能根据网络当前的状态及时地进行路由更新，从而使得部分星间链路负载加重而发生拥塞，数据包排队时延增大，需等到下一个连通时间片才能将数据包转发到下一跳节点。因此，DVTR算法的平均时延要高于ACO-PRA算法。而IACO算法的平均时延稍高于ACO-PRA算法，这是由于IACO算法没有考虑链路剩余带宽和链路容量，只是单一的根据链路上信息素大小来选择下一跳，容易造成最优路径业务流增大，链路中排队等待转发的包增多，这样就增加了IACO算法的时延性能。

图7 LEO卫星网络中的平均时延性能Fig.7 Average delay performance in LEO satellite networks

LEO卫星网络中的丢包性能如图8所示。从图8中可看出， ACO-PRA算法和IACO算法的丢包率性能均逐渐降低并趋于稳定，而DVTR算法的丢包率性能增大到一定幅度而趋于平稳。这是因为DVTR算法在链路的切换或断开时，路由表不能根据网络拓扑的动态特性及时地调整路由方案，源节点计算的路由失效而造成数据包的丢失数增大。同时，IACO算法的丢包率总是低于ACO-PRA算法。因为IACO算法并没有考虑到卫星间的星间距离和ISLs的链路容量，在同样的连通拓扑结构内，ACO-PRA算法能够满足业务流要求，优先选择链路剩余容量大的卫星节点，保证数据包及时地传输到目的节点。此外，IACO算法总是寻找最优路径，导致最优路径上的业务流增大而发生拥塞，目的节点无法准确地接受而造成数据包丢失。因此，随着算法迭代次数的增加，IACO算法的丢包率总是高于ACO-PRA算法。

5 结束语

针对卫星网络拓扑时变、链路连接性差等问题，提出了一种基于蚁群优化的概率路由算法(ACO-PRA)。首先，将网络拓扑周期均匀分为若个时间片而生成不同时刻的拓扑连通图；其次，将星间链路带宽和链路容量作为约束条件建立优化模型；最后，根据生成的节点概率函数选择下一跳卫星节点，找到一条满足约束条件的最佳传输路径。仿真结果表明，所提出的ACO-PRA算法不仅能够降低网络平均端到端时延和丢包率，还能提高网络吞吐量。

图8 LEO卫星网络中的丢包率性能Fig.8 Packet loss rate performance in LEO satellite networks

参考文献：

[1] ARANITI G, BEZIRGIRGIANNIDIS N, BIRRANE E, et al. Contact graph routing in DTN space networks: overview, enhancements and performance[J]. IEEE Communications Magazine, 2015, 53(3):38-46.

[2] LIU Ziluan, HAN Jiangxue, WANG Ying, et al. Performance analysis of routing algorithms in satellite network under node failure scenarios[C]//IEEE Global Communications Conference. Austin, TX: IEEE Press, 2014:2838-2843.

[3] 卢勇,赵有健,孙富春.卫星网络路由技术[J]. 软件学报, 2014, 25(5):1085-1100.

LU Yong, ZHAO Youjian, SUN Fuchun. Routing techniques on satellite networks[J]. Journal of Software,2014,25(5):1085-1100.

[4] CHANG H S, KIM B W, CHANG L, et al. FSA-based link assignment and routing in low-earth orbit satellite networks [J]. IEEE Transactions on Vehicular Technology,1998, 47(3):1037-1048.

[5] PAPAPETROU E, PAVLIDOU F N. Distributed Load-Aware Routing in LEO Satellite Networks[C]//IEEE Global Telecommunications Conference. New Orleans, LO: IEEE Press, 2008:1-5.

[6] HUSSEIN M, JAKLLARI G, PAILLASSB B. On routing for extending satellite service life in LEO satellite networks[C]//IEEE Global Communications Conference.Austin, TX: IEEE Press, 2014:2832-2837.

[7] YANG Yuan, XU Mingwei, WANG Dan, et al. Towards Energy-Efficient Routing in Satellite Networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12):3869-3886.

[8] WU Zhaofeng, HU Guyu, JIN Fenglin, et al. Agent-based dynamic routing in the packet-switched LEO satellite networks[C]//IEEE International Conference on Wireless Communications & Signal Processing. Nanjing, China: IEEE Press, 2015:1-6.

[9] 杨力,孙晶,潘成胜.基于多目标决策的LEO卫星网络多业务路由算法[J]. 通信学报, 2016, 37(10):25-32.

YANG Li, SUN Jing, PAN Chengsheng. LEO multi-service routing algorithm based on Multi-objective decision making[J]. Journal of Communications,2016, 37(10):25-32.

[10] DORIGO M, MANIEZZO V, COLORNI A.The Ant System: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1996,26(1):29 - 41.

[11] LONG Fei, SUN Fuchun. An Improved Ant Colony Algorithm and Its Application In Routing Computation of Satellite Networks[C]//IEEE IMACS Multiconference on Computational Engineering in Systems Applications. Beijing: IEEE Press, 2006:1567-1573.

[12] GAO Zihe, GUO Qing, WANG Ping. An Adaptive Routing Based on an Improved Ant Colony Optimization in LEO Satellite Networks[C]//IEEE International Conference on Machine Learning and Cybernetics. Hong Kong, China: IEEE Press, 2007:1041-1044.

[13] WANG Houtian, ZHANG Qi, XIN Xiangjun,et al. Cross-layer design and ant-colony optimization based routing algorithm for low earth orbit satellite networks[J]. China Communications, 2013, 10(10):37-46.

[14] BHATIA A, JOHARI R. Genetically optimized ACO inspired PSO algorithm for DTNs[C]//IEEE 3rd International Conference on Reliability,Infocom Technologies and Optimization. Noida: IEEE Press, 2015:1-6.

[15] MOHAMED A, RACHID E K, BELLAFKIH M, et al.AntProPHET: A New Routing Method for Delay Tolerant Networks [C]//Mediterranean Microwave Symposium. Marrakech: IEEE Press,2015:1-6.