具有特定结构的离散型八进对称正交小波
2018-07-02杨梦云
杨梦云
(1.邵阳学院 理学院,湖南 邵阳,422000;2.中南大学 信息科学与工程学院,湖南 长沙,410083)
二进小波理论正在日趋成熟,小波变换在JPEG2000中的应用,让小波技术有了里程碑式的标志,其中著名的双正交小波滤波器有5-3型和9-7型[1]。在理论方面,Daubechies在文献[2]中证明了除Haar 小波以外的所有实紧支撑的二进正交小波都不具有对称性或反对称性。而在多进小波里,线性相位和正交性的矛盾就不再存在,因此构造多进小波显得十分有必要。在实际应用方面,如果能对信号进行更精细的分析,那么实际应用的效果也会更好[3]。如对图像进行小波分解时,二进小波分解一次产生3个高频子块,四进小波分解一次产生15个高频子块,而八进小波分解一次则可产生63个高频子块,显然它所包含的高频信息更丰富,因此八进小波为更精细的信号分析提供了更多可能性。
在四进小波中,文献[4-6]做出了不少具有理论价值的工作,他们设计出来的大多数小波不是应用所期望的。王国秋教授在文献[7-8]中给出了16-8型双正交小波,它在图像压缩上性能超过了9-7型双正交小波。在众多四进小波理论和实际应用中,文献[9-15]提供了有潜在应用价值的小波基,特别是文献[9,10,12]所设计的四进正交小波基的共同特点是一支低通滤波器通过改变符号和位置来生成其余三支高通滤波器,并且只要低通滤波器满足正交性条件,其他三支高通滤波器就自动满足正交性。但是彭中立教授在文献[9]中指出将四进小波的结构推广到八进小波时,并不能只在低通滤波器满足正交性条件下,生成对应的八进正交小波。因此,文中以彭立中教授和王国秋教授设计出的四进正交小波滤波器为基础,设计出了具有特定结构的八进正交小波类,它可由一支低通滤波器通过改变符号和位置来生成其余七支高通滤波器,在求解滤波器系数的过程中大大减少了未知量的个数,这类八进小波不但滤波器都具有对称性或反对称性,而且还能将多出来的自由度用到实际应用中。
1 多进小波的多分辨分析

①
在L2(R)中稠密;
②f(x)∈Vj当且仅当f(mx)∈Vj+1;
③存在Φ(x)∈V0,{Φ(x-i)}i构成V0的标准正交基。
关于多进小波的尺度函数和小波函数有如下的一些基本事实:尺度函数Φ(x)具有如下的形式:
其中hi是实数,称为低通滤波器。m-1个小波函数{Ψ(k)(x)},k=1,2,…m-1具有如下的形式:
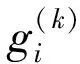
(1)
(2)
(3)
其中δj是一个脉冲信号。公式(1)、(2)和(3)是构造多进小波的必要条件,同时,若滤波器组满足这些正交条件,则具有完全重构性质。
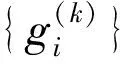
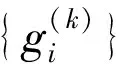
消失矩是衡量小波性能的一个重要指标,消失矩的高低直接影响着矩阵的稀疏程度。特别是在图像压缩的过程中,高的消失矩可以使变换矩阵的能量更集中,从而得到较高的压缩率。因此在实际应用中,通过设计出具有较高消失矩阶数的滤波器,使其小波具有好的压缩性能。
2 构造具有特定结构的八进对称正交小波滤波器组
在二进小波中,若公式(1)成立,则只需把低通滤波器的系数通过倒序交替和改变符号就能得到对应的高通滤波器,并且公式(2)和(3)自动成立,这就为设计和构造滤波器带来了极大的方便。但对于多进小波的构造却没有这个性质,因此文中通过巧妙地构造得到了一类具有此性质的八进正交小波滤波器,即它的七支高通滤波器都是由低通滤波器通过改变符号和位置所生成的。

{hi}={h1,h2,…,h4L-1,,h4L,,h4L,,h4L-1,,…,h2,h1},(1≤i≤8L)
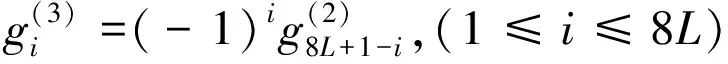
例如,当L=2时,八进对称小波系统为
其中第1,3,5,7行是对称的,第2,4,6,8行是反对称的。


即hi=h8L+1-i
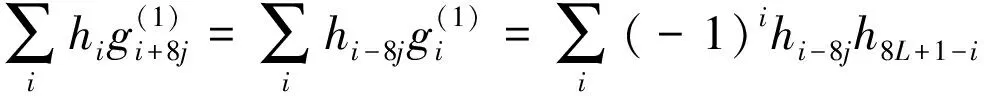




其中
(令p=4L+4j-i+1)

同理可证
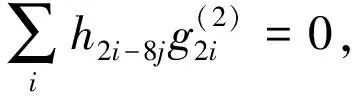
最后证明


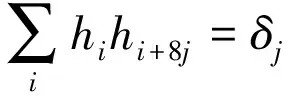
3 实例


{hi}={0.00120106,-0.0242213,-0.0277497,-0.0421235,-0.0429359,0.0156321,0.0633546,0.132971,0.219381,0.314420,0.365671,0.438613,...} (其余系数对称)。

{hi}={0.0122761,-0.04518871,-0.02893991,-0.0569193,-0.03482223,0.03735133,0.06529673,0.166956,0.174322,0.333445,0.345142,0.445295,...} (其余系数对称)。

{hi}={0.00173534,0.00149443,0.00229963,0.0000164103,0.0154146,0.00309932,
0.00394514,-0.00765034,-0.0410593,-0.0464078,-0.036929,-0.0258219,-0.0345212,0.0277628,0.0591762,0.132392,0.268136,0.3353454,0.357321,0.398465,…}(其余系数对称)。
设该组滤波器相应的尺度函数为φ,小波函数为ψi(i=1,2,…,7),并画出了尺度函数和小波函数的图形(见图1),可以看出φ和ψi(i=1,2,…,7)都有较好的光滑性,相信它在图像处理方面会有较好的应用,在这里给出了Lena图像的分解图(见图2)。

图1 尺度函数φ和小波函数ψi(i=1,2,…,7)Fig.1 The graphs of the scaling function φ and wavelet functions ψi(i=1,2,…,7)

图2 Lena图像的分解图Fig.2 The decomposition image of Lena
4 小结
文章系统地研究了一类八进正交小波,该小波具有紧支撑集、对称性、高阶消失矩和构造方法简明的特点。对于应用研究者而言,可以结合自己的实际研究背景用该方法设计出适合自己的八进小波。在八进小波中,由于有限的自由度要作用到七支高通滤波器上,这就会使得八进小波的消失矩没有二进小波的高。因此如何分布八进高通滤波器的消失矩阶数能使小波性能达到最优,这是以后要进一步研究的内容。
参考文献:
[1]DAUBECHIES I.Orthonormal bases of compactly supported wavelet[J].Communications on Pure and Applied Mathematics ,1988,41(07):909-996.
[2]DAUBECHIES I.Ten lectures on wavelets[M].Philadelphia:Society for Industrial and Applied Mathematics,1992.
[3]BI N,SUN Q Y,HUANG D R,et al.Robust image watermarking based on multiband wavelets and empirical mode decomposition[J].IEEE,Transactions on Image Processing,2007,16(08):1956-1966.
[4]黄达人,毕宁,孙颀彧.多进制小波分析[M].杭州:浙江大学出版社,2001.
[5]HAN B.Symmetric orthogonal scaling functions and wavelets with dilation factor 4[J].Advances in Computational Mathematics,1998,8(03):221-247.
[6]彭立中,王永革.3带正交小波系统的参数化和代数结构[J].中国科学(A辑),2001,31(07):602-614.
[7]WANG G Q,ZOU Q Y,YANG M Y.Sub-band operators and saddle point wavelets[J].Applied Mathematics & Computation,2014,227(c):27-42.
[8]王国秋,杨梦云.双正交小波的谱半径及其应用[J].湖南师范大学自然科学学报,2011,34(01):14-18.
[9]彭立中,王永革.具有优美结构的紧支正交小波的构造[J].中国科学E辑:技术科学,2004,34(02):200-210.
[10]WANG G Q.Four-bank compactly supported bi-symmetric orthononnal wavelets bases[J].Optical Engineers,2004,43(10):2362-2368.
[11]WANG G Q.Matrix methods of constructing wavelet filters and discrete hyper-wavelet transforms[J].IEEE,Optical Engineering,2000,39(04):1080-1087.
[12]郑果,张平柯,王国秋.四进正交小波基在图像压缩上的应用[J].计算机工程,2012,38(01):227-229.
[13]ZOU Q Y,WANG G Q.Optimal model for 4-band biorthogonal wavelets bases for fast calculation[J].Journal of Inequalities & Applications,2017,2017(222):1-10.
[14]BHATI D,SHARMA M,PACHORI R B,et al.Time-frequency localized three-band biorthogonal wavelet filter bank using semidefinite relaxation and nonlinear least squares with epileptic seizure EEG signal classification[J].Digital Signal Processing,2016,62.
[15]CEKIC Y,EREN L.Broken rotor bar detection via four-band wavelet packet decomposition of motor current[J].Electrical Engineering,2017,(12):1-6.
