基于尖Γ云模型的基因表达式编程算法研究

姜 玥，何林霖，刘 倩

(西南民族大学计算机科学与技术学院，四川 成都 610041)

基因表达式编程(Gene Expression Programming，GEP)是函数关系挖掘的新方法，它继承和发展了遗传算法(Genetic Algorithm，GA)和遗传编程(Genetic Programming，GP)[1]，克服了 GA与 GP的不足，更适合于函数关系的挖掘.然而，文献[2]提出的GEP算法，采用了固定的变异率和交叉率，没有考虑样本的具体分布和适时进化状态.文献[3-6]将GEP算法应用于多个领域.文献[7-8]对遗传算法进行改进，分别应用到AGV最优路径规划和堆石料的参数反演.文献[9]提出采用交叉模型的GA，改进了交叉的方式，但是依然忽略了变异率的动态变化，并且GA是线性编码解决简单问题，难以解决复杂问题.文献[10]研究了遗传规划中，遗传算子对种群多样性的影响.文献[11]在遗传规划中，采用分级与截取相结合的选择方法，动态选择变异的策略.但是，忽略了个体适应度分布的形态变化.中国的李德毅教授提出的云模型[12]已成功应用于数据挖掘、智能控制和入侵检测等领域.众多的统计分布都和Γ分布有关.由于许多客观事物的特征具有模糊性，为了让GEP算法能模拟人的思维方式对进化过程中的核心参数进行识别和调整，本文提出基于将Γ型隶属函数引入GEP算法，改进传统GEP的变异和交叉，使GEP算法在进化过程中跳出早熟和局部最优，有效地提高收敛速度，延长有效进化寿命.

1 基本概念

Γ型隶属函数是模糊集理论中常用的一种.由于Γ分布于指数分布的等价性，常简化为指数形式.指数分布是在可靠性研究中最常用的一种分布形式.在进化的种群中，指数形式可以用来近似地描述个体分布.为了方便描述，定义了以下概念，其中exp为指数函数.

定义1 设Ex，En和He分别为期望值，熵和超熵，G为种群

1)(云模型)设U＝{x}，T为U上的语言子集，CT(x):U✍[0，1]，∀x∈U，称CT(x)在 U 上的分布为云模型.

2)(尖Γ云模型)设 R(Ex，En，He)为尖 Γ分布的隶属函数，满足方程组:

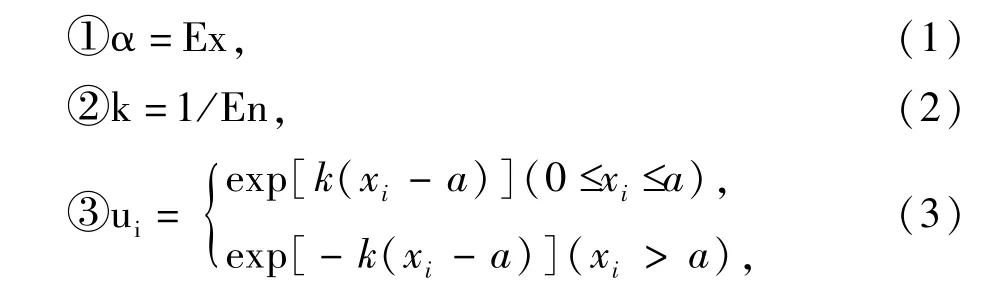
的数据对 Drop(xi，ui)(i＝1，2，…)组成的 CT(X)称为尖Γ云模型，简称尖Γ云，记为(Ex，En，He).组成CT(X)的数据对(xi，ui)称为尖Γ云滴.尖Γ云如图1所示.

3)(GEP模式)设N为个体数，M为基因数，Q为种群数，则 GEP模式 ＝(N，M，Q)，即

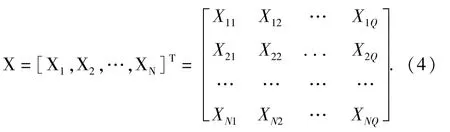
4)(适应度隶属度)设fi为Indi的适应度值，则

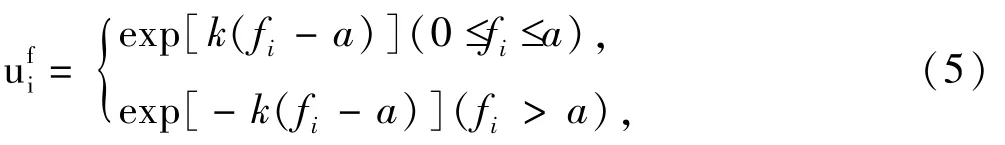
称为Indi的适应度隶属度.

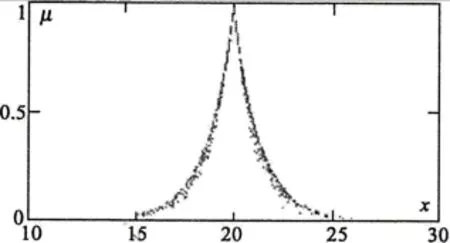
图1 尖Γ云Fig.1 Cusp Gamma Cloud

2 尖Γ云调整算法

观察1 恒定的变异率或交叉率使进化早熟收敛.

进化过程中，如果自始至终采用恒定的变异率或交叉率，而不考虑进化的当前状态，减小了个体的多样性，导致进化早熟收敛，达不到全局最优.

尖Γ云模型改善了严格规范和过度确定的弱点，它将概念的模糊性和随机性集成在一起.变异率和交叉率是决定GEP性能的关键.利用模糊集理论中的尖Γ型的隶属函数，扩展为尖Γ云，设计尖Γ云调整算法将模糊性溶于使变异率和交叉率的主动调整中，跟随适应度适时动态改变.

定义2 设种群 G，∀Indi，Indj∈G，favg＝∑fi/Q，fmax＝Max(fi)，fmin＝ Min(fi)，1≤i≤Q，Q 为种群数，Max为最大值函数，Min为最小值函数，fi为Indi的适应度.期望值 Ex＝favg，熵 En＝Cn(fmax-fmin)，超熵 He＝CeEn，En’ ＝ R(En，He)，Cn，Ce为常数，调节因子.

(1)(尖Γ云变异率)则尖Γ云变异率

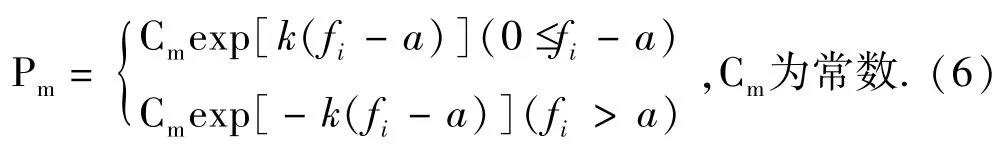
(2)(尖Γ云交叉率)则尖Γ云交叉率

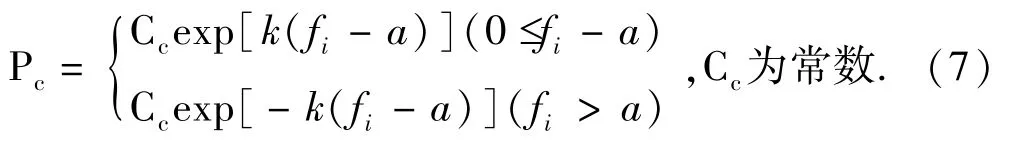
定理1 设尖Γ云变异率Pm.当fi＝α时，Pm＝Cm；当 fi＞ ＞α 时，Pm∞0.

证明:因为式(6)

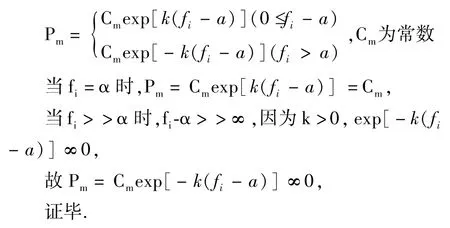
当fi＝α时，即个体的适应度与种群平均适应度一样，反映了该个体与种群中的个体比较相似，那么就必须加大变异率，以刺激种群多样性的产生；反之，当fi＞＞α时，即个体的适应度远远高于种群平均适应度，进化良好，因此，此时不适合立刻加大种群的变异，而应让此时的良性进化持续一定时间.

定理1表明正态分布广泛存在于自然界、生产及科学技术的许多领域中.但是，在实际应用中，尽管有大量因素影响着结果，但是各因素的权重不同，往往可能只是其中的少数几个因素处于核心地位.因此，直接将正态分布应用于实际，无法真实地反映客观情况.定理1中的α是形状参数，形状参数a越大，形状越扁.将尖Γ隶属函数扩展到云模型.通过云模型中的量化云滴，能比较好地进行解释.He反映某几个因素的不均衡性.指数分布e(k)的期望值和标准差均为1/k.尖Γ云的生成算法分为两步，(1)通过给定的数字特征值(Ex，En，He)得到 k；(2)通过 k生成指数随机数[17].

定理2 设尖Γ云交叉率Pc.当fi＝α时，Pc＝Cc；当 fi＞ ＞ α 时，Pc∞0.

定理2的证明与定理1的证明同理.

采用尖Γ云调整算法的基本思想是:①计算Ex，En和He；②生成以1/En为参数的指数随机数E(1/En)；③生成以1/He为参数的指数随机数E(1/He)；④计算尖 Γ云变异或交叉率 Pm或 Pc，令(fi，Pm)或(fi，Pc)为云滴.尖Γ云变异或交叉率发生器如图2所示，尖Γ云发生器通过输入3个数值特征形成合乎条件的云滴.

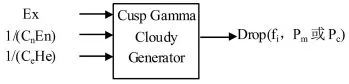
图2 尖Γ云发生器Fig.2 Cusp Gamma Cloudy Generator

算法1(CGCAA):尖 Γ云调整算法(Cusp Gamma Cloudy Adjust Algorithm，CGCAA)

输入:尖Γ云的控制参数Cn，Ce，种群Population

输出:云滴Drop(fi，Pm)或Drop(fi，Pc)

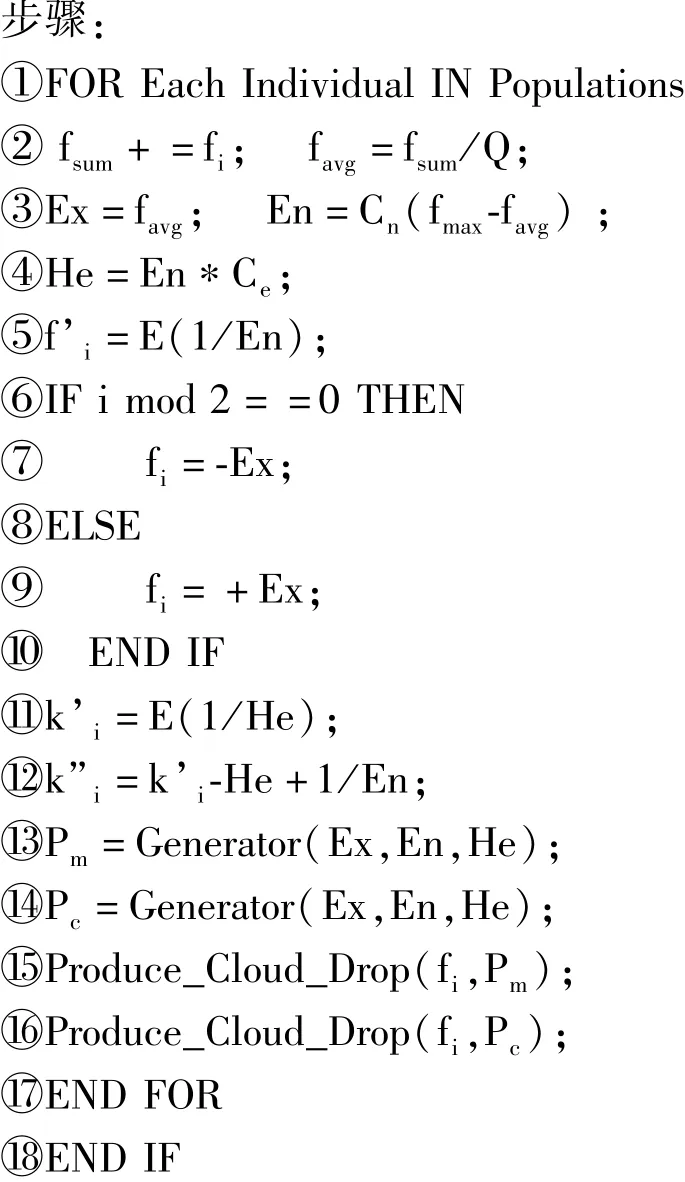
算法1中第13行和第14行分别通过尖Γ云变异和交叉发生器生成Pm和Pc.Ex和En的变化影响云的水平位置和陡峭程度，He和云滴的离散程度呈正比.He控制着云滴沿着期望曲线上下的分布情况.该算法生成的变异或交叉率自然地具有不均匀厚度的特征.

利用CGCAA算法产生的变异率和交叉率应用到传统GEP算法[1]，来改善传统GEP算法的性能，GEP算法的细节参考文献[2].

算法2(GEP-CGC):基于尖Γ云的GEP算法(Eene Expression Programming Based on Cusp Gamma Cloud)输入:样本数据集

输出:最优个体

算法2中，ε为误差阈值，MGeneration为最大进化代数.

命题1 算法2的时间复杂度为O(Q2)，其中Q为种群规模.

证明:外循环扫描每一个个体时的时间复杂度为O(Q)，在每一趟操作中，内循环的时间复杂度为O(Q).所以，总的时间复杂度是O(Q2).命题得证.

3 实验与性能分析

为了验证和比较策略的性能和有效性，将GEPCGC算法和传统GEP算法的实际运行效果进行实验和讨论，采用了Visual C＋＋6.0，运行平台为Intel Pentium 3.4GHz，4GB的 RAM 内存，1TB 硬盘，Windows 7操作系统.实验选择了学术界公认的3个函数进行测试.

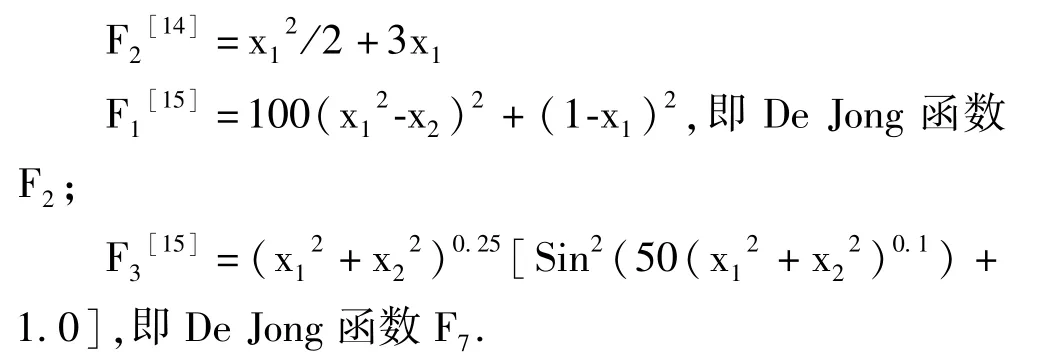
对各类GEP算法使用的参数如表1所示，其中S表示Sin函数.对以上函数产生的样本数据集重复80次挖掘实验，统计结果的进化性能如图3所示.

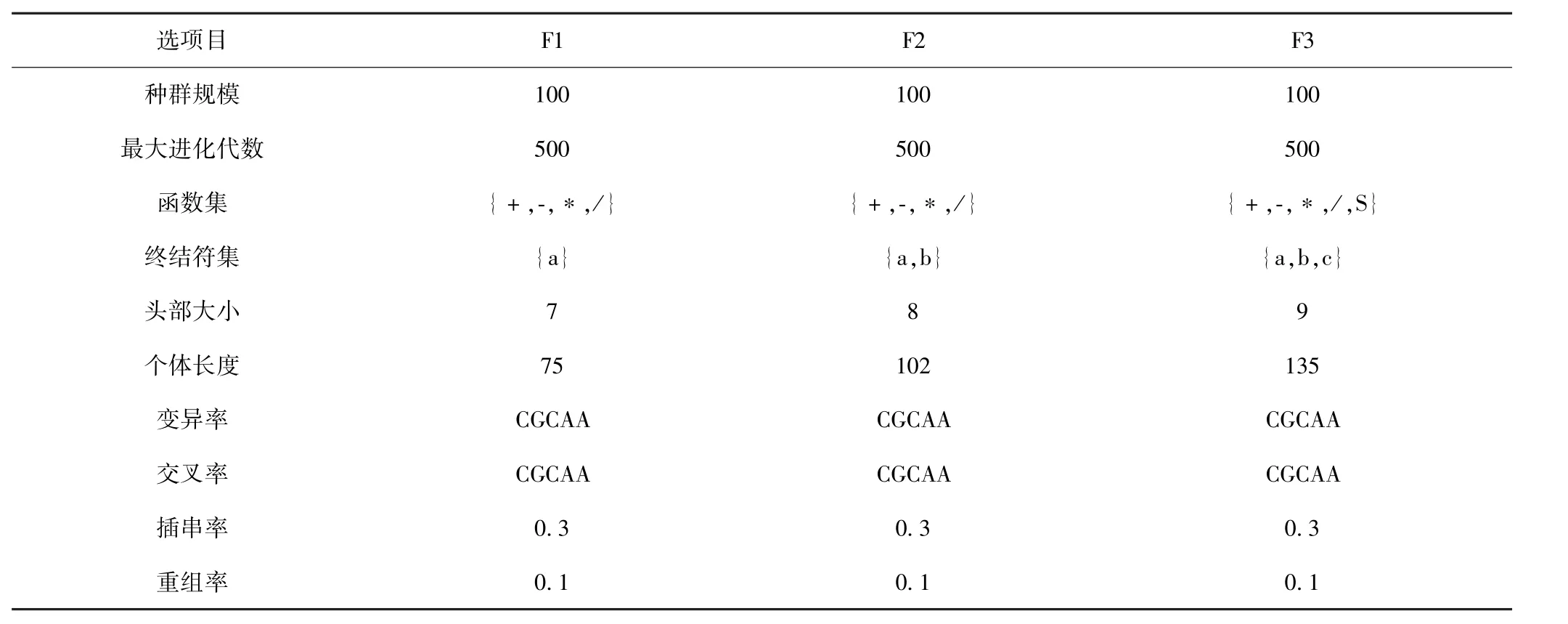
表1 GEP和GEP-CGC参数设置Table 1 Parameters for GEP and CGC

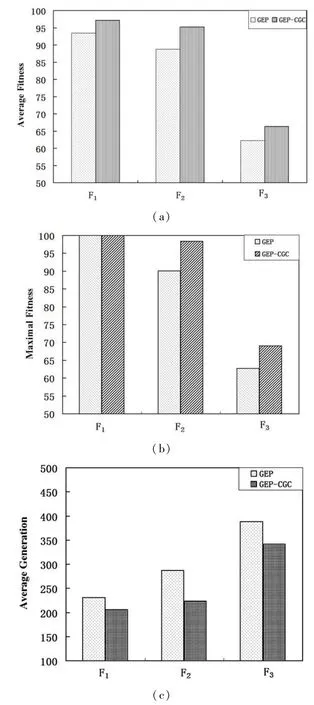
图3 进化性能Fig.3 The Performance of the Evolution

图3(a)是最优个体的平均适应度比较，可以看出GEP-CGC算法能够更好地跳出局部最优，寻求到更优解，最高适应度提高达7%.期望Ex反映了适应度云滴群的中心；熵En也就是论域中被模糊概念所接受的范围；超熵He即熵的熵，表现了云滴的离散程度，间接地反映了云的厚度.

图3(b)是最优个体的最高适应度比较，可以看出GEP-CGC算法明显提高了最高适应度.新算法通过尖Γ云模糊化改进后的算子使得种群根据种群当前状态调整变异和交叉的进程，增加了种群多样性，因而种群可以探索的空间扩大，进化收敛被延迟.种群可以更加活跃地进化，去逼近全局最优解.

延缓种群的过早同化.个体的相似是GEP进化的绊脚石，GEP算法要发挥良好的性能，需要个体的千姿百态为基础.GEP-CGC算法根据种群进化的现状，自动调整变异率和交叉率，明显改善了GEP的搜索性能，提高最高适应度约8%.尖Γ云借助云模型的定性定量间的不确定转换改进变异率和交叉率.Ex的变化掩盖了En取值不同带来的进化结果的差异.

尖Γ云模型具有最基本的云的特点，云是由许多云滴构成.与我们事实上观察一致的是，越靠近云的中心位置或者远离云的中心位置，隶属度的随机性就越小；距离云的中心位置不近不远的，隶属度的随机性就大[17].CGCAA算法生成的调整云自然地具有云的特性，通过R(Ex，En，He)，三个特征值足以很好地描述整个云的形态.图3(c)是最优个体的平均进化代数比较.说明CGCAA算法充分发挥云的作用来改善收敛速度，并且，也能避免进化过早结束.有效的进化过程被延缓，同时，有效进化的进程被加速，平均减少进化代数约10%.

4 结论

传统GEP算法使用一成不变的变异率和交叉率，不能很好地适应动态变化的进化过程.本文针对这一问题，在传统GEP算法的基础之上，提出了引入尖Γ云模型，并加以解决.实验表明GEP-CGC算法增加了个体的多样性，体现出较快的搜索速度，较好的收敛结果，具有很强的摆脱局部最优的能力.实验结果表明，平均适应度提高达7%，最高适应度提高8%，平均进化代数下降达10%.

下一步的工作，我们将在本文的基础上继续研究通过自学习逐步修正所选的近似的隶属函数，使之更加符合客观实际问题.

[1] 贾晓斌，唐常杰，左劼，等.基于基因表达式编程的频繁函数集挖掘[J].计算机学报，2005，28(8):1247-1254.

[2] CANDIDA.Ferreira Gene Expression Programming:A New Adaptive Algorithm for Solving Problems.Complex Systems[J]，2001，13(2):87-129.

[3] 彭昱忠，元昌安，李洁，等.个体最优共享GEP算法及其气象降水数据预测建模[J].智能系统学报，2016，11(3):402-409.

[4] 姜玥，谈文蓉，崔孟天，等.基于种群密集度的GEP算法挖掘药物不良反应[J].计算机应用研究，2015，32(10):2943-2946.

[5] 王斌，张迅，盛津芳，等.优化的GEP算法在爆破振动预测中的应用[J].计算机工程与应用，2016，52(22):212-217.

[6] 张锐，侯沙沙.种群多样性的GEP算法在预测中的研究和应用[J].哈尔滨理工大学学报，2017，22(4):18-22.

[7] 赵大兴，余明进，许万.基于高适应度值遗传算法的AGV最优路径规划[J].计算机工程与设计，2017，38(6):1635-1641.

[8] 曾辉，廖露梅，曾予剑.遗传算法—支持向量机在面板堆石坝堆石料的参数反演分析的应用[J].江苏水利，2017，8:34-37.

[9] 杨新武，杨立军.基于交叉模型的改进遗传算法[J].控制与决策，2016，31(10):1837-1844.

[10] 周冬梅，孙俊.遗传规划中遗传算子对种群多样性的影响[J].计算机工程与应用，2016，52(20):39-45.

[11] 郝艳伟，李祖枢.一种改进的遗传规划算法[J].重庆理工大学学报(自然科学版)，2011，25(4):74-78.

[12] 李德毅，孟海军，史雪梅.隶属云和隶属云发生器[J].计算机研究与发展，1995，32(6):15-20.

[13] 姜玥，崔孟天，吴江，等.基于条件云的基因表达式编程算法[J].计算机应用研究，2015，32(4):1107-1109.

[14] CANDIDA.Ferreira Gene Expression Programming[EB/OL].[2018-02-08]. http://www.gene-expression-programming.com/gep/Gep-Book/Chapter4/Section1/SS2.htm.

[15] ZBIGNIEW MICHALEWICZ.Genetic Algorithms＋Data Structures＝Evolution[M].Berlin Heidelberg:Springer-Verlag，1999:349-350.

[16] NGA LAM LAW，SZETO K Y.Adaptive Genetic Algorithm with Mutation and Crossover Matrices[C].IJCAI-07:2330-2333.

[17] 李梅.不完备信息下的河流健康风险预估模型研究[D].西安:西安理工大学，2007.