方程求根的一个四阶迭代算法

龙爱芳

(中南民族大学数学与统计学学院，湖北 武汉 430074)

1 引言

求解非线性方程和超越方程f(x)＝0的方法很多，迭代法是应用非常广泛的一种方法，迭代算法有很多新的研究成果[1－7]而Newton迭代法是最常用的方法，它具有形式简单，收敛速度快等特点，具有二阶的收敛速度.除此之外还有很多修正的Newton迭代算法[8－13].应用微分中值定理的渐近性，结合线性插值，构造出了一个具有四阶收敛速度的新的迭代算法.

2 主要成果

先给出微分中值定理中间点的渐近性.

定理1[14](Taylor中值定理)如果函数f(x)在含有x0的某个开区间(a，b)内具有直到(n＋1)阶的导数，则对任一x∈(a，b)有

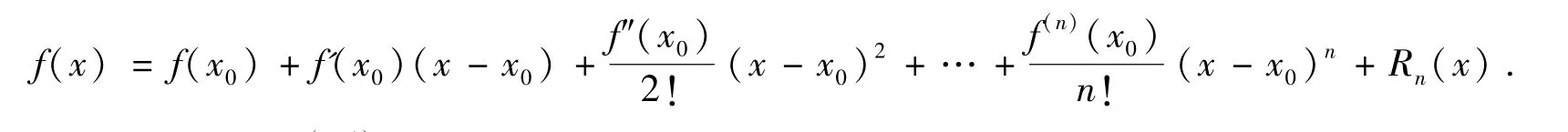
其中，这里ξ是x0与x之间的某个值.

取n＝1，得1阶的Taylor公式

定理2设f(x)在含有x0的某个开区间内具有直到3阶导数，且f'″(x0)≠0，则(1)式中的ξ具有如下的渐近性:

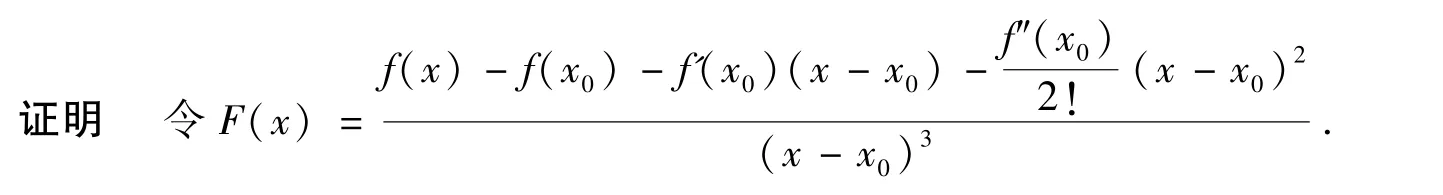
一方面，应用罗必塔法则及3阶导数的定义，有

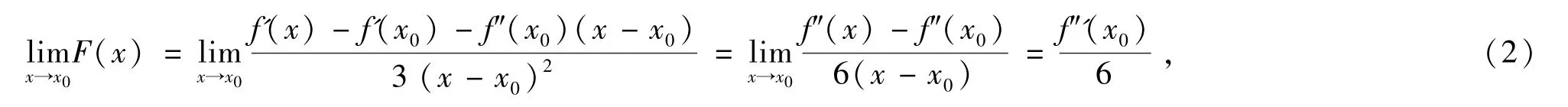
另一方面，应用(1)式及罗必塔法则，有

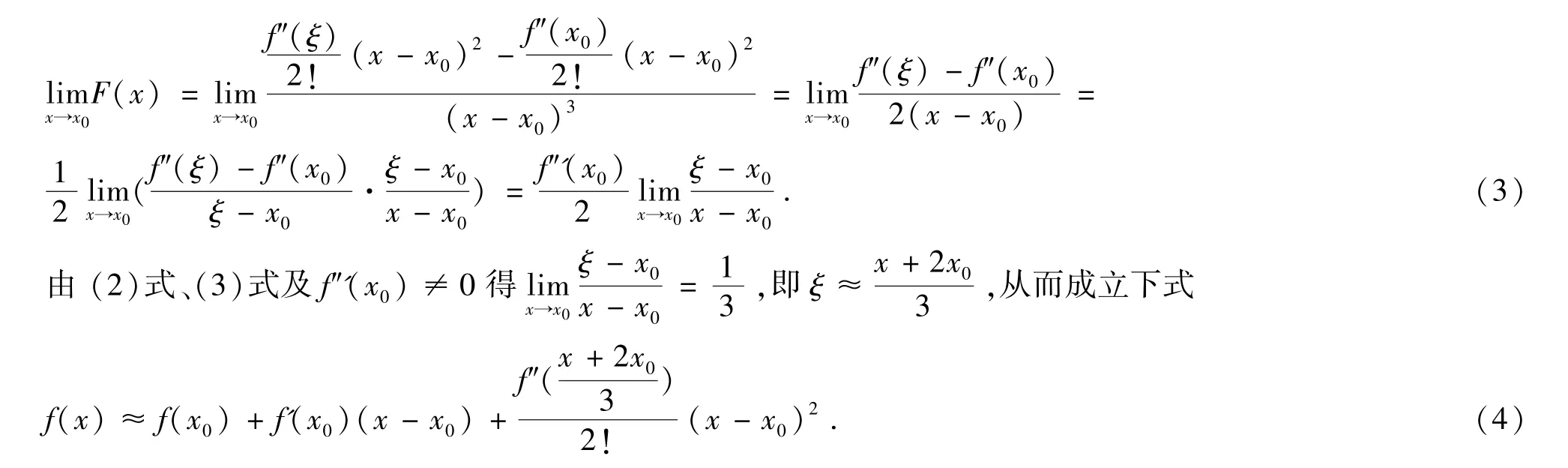
下面构造迭代公式.

设y＝f(x)的反函数为x＝φ(y)，按照反函数的求导法则有

设f(x*)＝0，f(xk)＝yk则有x*＝φ(0)，xk＝φ(yk)，φ(0)应用(4)式得

下面给出收敛性证明.

定义1[15]设迭代公式xk＋1＝φ(xk)收敛于方程x＝φ(x)的根x*，如果迭代误差ek＝xk－x*当k→∞时成立下列渐近关系式:，则称迭代公式是p阶收敛的.

定理3设方程f(x)＝0的根为x*，函数f(x)在x*的某领域内具有连续的4阶导数，且f'(x*)≠0，则迭代公式(7)在x*邻近至少是4阶收敛的.

证明把f(xk)，f'(xk)在x*处Taylor展开，设并注意到f(x*)＝0，得

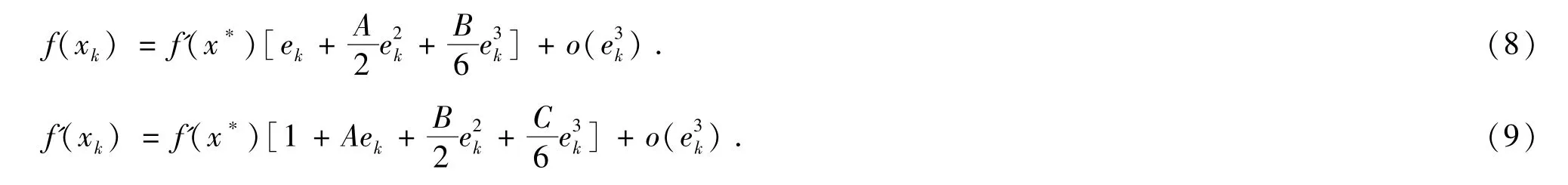
应用以上两式，得

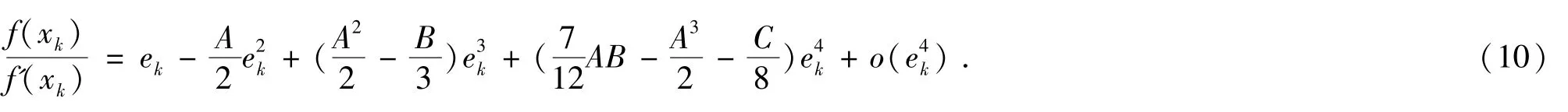
在两边同时减去x*，并应用(10)式得

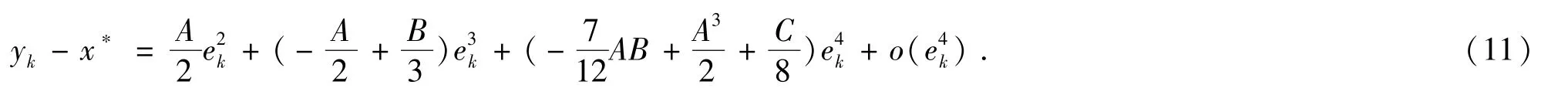
把f″(xk) 在x*处Taylor展开，得

应用(8)式、(9)式及(12)式得

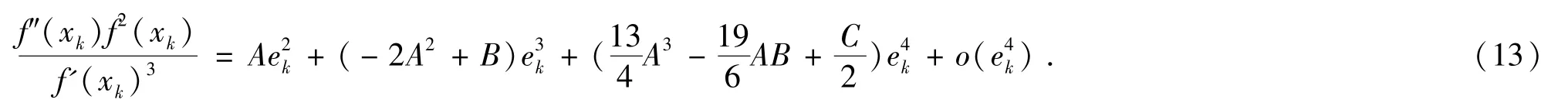
把f'(yk)，f″(yk)在x*处Taylor展开，并应用(11)式得

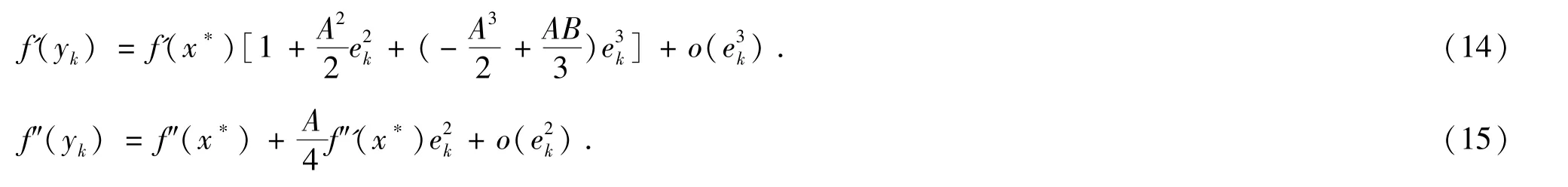
应用(8)式、(14)式及(15)式得

在公式两边同时减去x*，并应用(11)式、(13)式及(16)式得ek＋1＝，因而有，由定义1知迭代公式(7)有4阶的收敛速度.

3 数值试验

例1 求方程f(x)＝x3－x－1＝0在区间[1，2]上的根.精确根为x*＝1.324717957244746….

表1 例1的数值试验结果(取迭代初值x0＝8)Table 1 The numerical result of example 1(The initial value of the iteration x0＝8)

例2求方程f(x)＝cosx－xex＋x2＝0在区间[1，2]上的根.精确根为x*＝0.639154096332….

表2 例2的数值试验结果(取迭代初值x0＝5)Table 2 The numerical result of example 2(The initial value of the iteration x0＝5)

例3求方程f(x)＝x5＋x4＋4x2－15在区间[1，2]上的根.精确根为x*＝1.347428098968….

表3 例3的数值试验结果(取迭代初值x0＝8)Table 3 The numerical result of example 3(The initial value of the iteration x0＝8)

从以上表1-3三个算例可以看出，迭代公式(7)的收敛速度是相当快的，说明该迭代公式是非常有效的.

[1] 吴新元，欧阳梓祥，赵大伟.不用计算导数的大范围收敛迭代法[J].高等学校计算数学学报，1998，4:377-388.

[2] 郑权.具有参数的不带有导数的平方收敛的迭代法[J].计算数学，2003，25(1):107-112.

[3] 魏焕彩，郑修才.一种两点迭代法[J].工科数学，1999，15(1):160-163.

[4] 高尚.不动点迭代的一点注记[J].大学数学，2003，19(4):16-19.

[5] 邸书灵，刘展威，刘玉宏.关于非线性方程加速迭代的注记[J].工科数学，2002，18(5):82-86.

[6] 欧志英，严克明，雷东侠.解非线性方程的二阶敛速的s迭代法[J].西北民族学院学报(自然科学版)，2003，24(47):18-20.

[7] 龙爱芳.一类避免导数计算的一个新的迭代公式[J].大学数学，2017，33(2):108-110.

[8] HAN DANFU，WANG XINHUA.The error estimates of Halley’s method[J].Numerical Mathematics，1997，6(2):231-240.

[9] 王兴华，郭学萍.Newton法及其各种变形收敛性的统一判定定理[J].高等高等学校计算数学学报，1999，21(4):363-368.

[10] 郭学萍.避免二阶导数计算的迭代族的收敛性[J].工程数学学报，2001，18(4):29-34.

[11] 吴新元.对牛顿迭代法的一个重要修改[J].应用数学和力学，1999，20(8):863-866.

[12] 刘伟伟，田志远.方程求根的一个三阶算法[J].青岛大学学报(自然科学版)，2012，25(4):1-5.

[13] 陈新一.Newton迭代法的一个改进[J].数学的实践与认识，2006，36(2):291-294.

[14] 同济大学数学系.高等数学(第六版上册)[M].北京:高等教育出版社，1978.

[15] 李庆扬，王能超.数值分析[M].武汉:华中科技大学出版社，1986.