考虑劣化因素的HMM在设备状态评估中的应用

廖雯竹，崔诗好

(重庆大学 机械工程学院，重庆 400044)

0 引言

随着机械设备结构与功能的日益复杂和自动化程度的日益提升，人们对设备安全性和可靠性的要求越来越高，愈加关注设备的状态评估及预测。在历经事后维修、基于时间的预防性维护后，基于状态维护(Condition Based Maintenance, CBM)成为研究热点。对设备状态进行准确评估作为实现良好状态维护的关键，已经成为备受国内外学者关注的重要问题之一[1]。

现有的设备故障诊断方法分为定性与定量分析两大类，其中定性方法主要有定性仿真、专家系统、抽象分层和图论方法等；定量方法主要基于解析模型和数据驱动的故障诊断方法，如人工神经网络(Artificial Neural Networks, ANN)和隐马尔可夫模型(Hidden Markov Model, HMM)等智能诊断技术[2]。HMM最初应用于语音识别领域，Bunks等[3]根据CBM过程与语音识别过程的相似性，首次提出将基于状态的分类方法应用于直升机齿轮箱的视情维修的思想，同时对基于故障诊断的视情维修进行了可行性分析；随后，Atlas等[4]将HMM用于工具磨损的过程监控；Ertunc等[5]将连续隐马尔可夫模型(Continuous HMM, CHMM)用于钻井作业刀具磨损的状态监测与故障诊断；Dong等[6-8]开展了基于隐半马尔可夫模型(Hidden Semi-Markov Model, HSMM)的设备故障诊断、预测和健康管理研究；Wu等[9]通过改进前后向算法解决了HSMM运算时可能出现的下溢问题；Zhu等[10]提出一个依赖时间间隔因素的HSMM来预计设备剩余使用寿命(Remaining Useful Life, RUL)；Liu等[11]运用最大似然和线性回归的方法训练数据对RUL进行的预测。此外，一些学者还致力于改进传统HMM，例如龚勋等[12]利用机械设备的空间结构性对经典HMM模型进行补偿；Xia等[13]采用期望值最大法(Expectation Maximization, EM)训练优化模型参数，建立了基于HMM的设备健康状况评价模型；Liao等[14]提出一个集成模拟退火算法(Simulated Annealing, SA)和EM的混合算法优化参数；Le等[15]提出一种多分支HMM，用于描述多个衰退模式下的设备劣化过程；Yuwono等[16]提出一个基于群快速质心估计(Swarm Rapid Centroid Estimatio，SRCE)的故障诊断模型，并应用于轴承的故障诊断；Gao等[17]提出一个基于SA的k-means聚类算法对滚轴的故障状态进行分级，在此基础上使用HMM进行故障诊断。

在设备运行过程中，某些部件会随时间而磨损，或者裂纹增长、被腐蚀等，导致状态逐渐劣化。目前设备劣化模型按状态类型分为两大类：①离散状态劣化系统，如Markov或半Markov过程模型；②连续状态劣化系统，如Gamma过程[18]。HMM作为一种统计模型，可描述设备性能衰退规律与健康状态转移的双重随机过程。然而，传统HMM往往假定设备的状态转移概率为固定值，忽略了实际运行中，设备状态转移概率随时间增加发生变化的情况，即设备保持其原有状态的概率会变小，而转移到更差状态的概率会增加。针对该问题，本文提出一个考虑劣化因素的HMM，并通过开发一个双重EM来估计HMM参数，以有效地进行设备状态评估。虽然以往文献(如文献[19-20])也有考虑劣化因素，但其大多假定初始状态的转移概率为已知，而实际情况中由于前期数据较少，该参数很难通过训练得到。本文除劣化因子外，还考虑了初始状态转移概率，并通过设计双重EM算法估算这两个参数值。此外，以往文献多是在HSMM中引入劣化因子，并与灰色理论等结合用于设备寿命预测，本文则采用一类新的指数型劣化因子设计方式构建新的HMM，以提高设备状态评估的可行性和有效性。

1 构建考虑劣化因素的HMM

1.1 HMM基本框架

HMM用于描述一个双重随机过程，即状态之间的转移过程以及状态和观测值之间的对应关系。其完整定义如下：

N为模型中状态的个数；

M为每个状态可以输出不同观测值的个数；

π=(π1,π1,…,πN)为初始状态概率分布，其中

(1)

A={aij}N×N为状态转移概率矩阵，aij表示从状态i转移到状态j的概率，其中

1≤i,j≤N；

(2)

B={bjk}N×M为观测值概率矩阵，bjk表示t时刻状态j出现观测值vk的概率，其中

1≤j≤N,1≤k≤M。

(3)

HMM记为λ=(π,A,B)，同时定义前向概率变量αt(i)、后向概率变量βt(i)及概率变量γt(i)。αt(i)是给定模型λ在时刻t输出观测序列{O1,O2,…,Ot}且设备处于状态θi的概率；βt(i)是给定模型λ在时刻t设备处于状态θi，在t+1时刻到最后时刻T输出的观测序列为{Ot+1,Ot+2,…,OT}的概率；γt(i)是给定模型λ和观测序列O，在t时刻设备处于状态θi的概率。

(4)

式中：t=1,2,…,T;i=1,2,…,N。根据式(4)，变量αt(i),βi(i),γt(i)计算如下：

(5)

1.2 考虑劣化因素的HMM

一般地，对于正常运行的设备而言，设备从健康逐渐劣化到失效会经历不同状态，例如从状态1、状态2直至状态N。在不同观测时间点，可观测得到该时刻的设备状态，该过程可看作为一个随机过程[21]。设备状态序列从状态i转移到状态j的概率即为转移概率aij，则转移概率矩阵

(6)

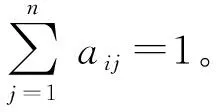
(7)

传统HMM可通过训练得到转移概率矩阵A，但一般认为设备各状态之间的转移概率固定不变，而且转移概率矩阵会呈现出一种特性，即当j>i时，aij随着j的增加而减小，因此转移概率矩阵每一行中aii都趋于最大值。

然而，设备在运行过程中的健康状态会逐渐恶化，即设备状态变得更差的可能性将增加，保持原状态的概率会变小[22]。在HMM中使用转移概率描述设备状态的转移过程，前面这种状况在HMM的表现即为原有状态概率的aii值将随设备运行时间的增加而变小，转移到更差状态的概率aij将增加。传统HMM未考虑设备运行过程中健康状态转移概率发生变化的情况，一般仅用固定值描述转移概率，该特性容易造成设备状态评估的偏差，因此本文提出一个考虑劣化因素的HMM(Age-dependentHMM)来克服传统HMM的不足，以提高设备状态评估的准确性。

设备劣化可认为是设备在不同状态间转移的一个过程(设为S)，有S={s1,s2,…,sk,…,sf},且sk∈(θ1,θ2,…,θN)，其中sk表示第k个观测时刻的设备状态，f表示观测序列样本容量，sf一般为设备的失效状态且1≤k≤f。则设备经历此劣化过程的概率为

P(S{s1,s2,…,sf-1,sf})=P(sf|sf-1)·

…·P(s3|s2)·P(s2|s1)。

(8)

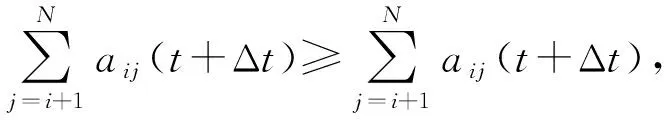
(9)

根据式(9)推导得

aii(t+Δt)=(aii(t))1+δ。

(10)

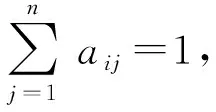
aii(t)-aii(t+Δt)=

(11)

因此，可推导

aij(t+Δt)=aij(t)+(aii(t)-

(12)

式中：1≤i≤N,1≤j≤N。

aii(kΔt)=(aii((k-1)Δt))(1+δ)1

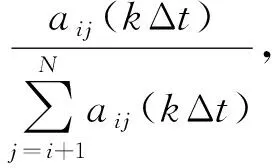
(14)

同理，根据式(12)和式(14)可得

aij(kΔt)=aij((k-1)Δt)+(aii((k-1)Δt)-

(15)

式中：1≤i≤N,1≤j≤N。由式(14)和式(15)可知，A0历经t=kΔt时刻后的转移概率矩阵

(16)

1.3 HMM参数估计

本文采用最大似然估计的方法估计劣化因子δ。已知A0和设备劣化过程的状态序列，当转移概率考虑了劣化因素时，式(8)可以进一步推导为

(17)

式中：Psksk+1表示设备状态由sk到sk+1的概率；1≤k≤f-1。

在估计劣化因子δ时，为排除偶发性，提高估计准确性，本文综合考虑多个劣化过程。假设有W个劣化过程序列，则似然函数

(18)

因此，δ的估计值可由最大化似然函数L的对数得到：

(19)

推导可得

(20)

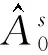
(21)

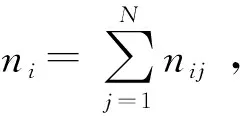
E(nij)=

1≤i≤N，1≤j≤N。

(22)

因此，A0中的

(23)

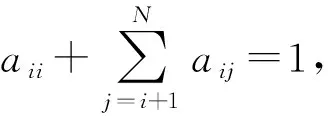
(24)

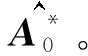
本文提出的双重EM算法的主要步骤描述如下：

步骤1初始化。设定AI0，迭代次数s=0，迭代步长iter_step。

步骤2令s++，劣化因子δ=s×iter_step。

步骤3根据式(23)和式(24)及δ，计算A0。

步骤4根据式(19)和A0，计算logL。

步骤5如果|logLs-logLs-1|≤ε(ε为预先设定的收敛条件)，则转步骤6，否则返回步骤2。

步骤6输出A0和s，结束。

这里，迭代步长iter_step和预先设定的收敛条件ε对算法的收敛速度和精度都有影响。理论上，更小的iter_step和ε可以得到更精确的结果，但是过小的iter_step意味着更长的时间，过小的ε意味着可能导致算法无法收敛，本文采用试值的方法确定iter_step和ε的值：首先选择一个稍大的iter_step和ε，已知δ∈(0,1)，若取iter_step=0.01，则可保证算法在100次内收敛，此时设置ε=0.01，根据收敛结果得到一个δ的值；再根据得到的δ，尽可能地缩小iter_step和ε，进一步估算δ。经过如此试算得到足够小的iter_step和ε，继而通过双重EM算法求解A0和δ。

2 基于Age-dependent HMM的设备评估

本文基于Age-dependent HMM对设备状态进行评估，评估流程如图1所示，主要分为数据收集处理、HMM构建和状态评估3部分。首先通过实时观测数据处理得到构建HMM所需的观测序列，然后通过上述算法得到A0和δ，接着通过构建的Age-dependent HMM计算设备处于各状态的概率，最后采用最大后验估计[24]确定设备状态。

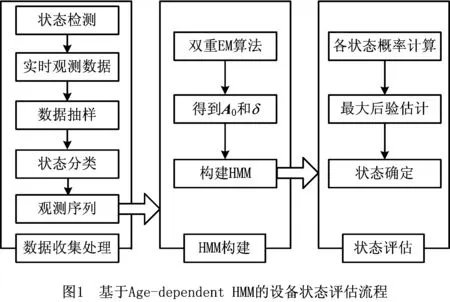
(1) 设备状态分类

设备随着持续运行，其健康状况将不断恶化，即经历一个劣化的过程。设备健康状态是通过一项或多项设备特征参数来反映的，如温度、压力、电压、振动信号等。通过状态监测得到设备的特征数据，通过数据处理可将设备的特征数据转为衡量设备健康状态的健康指标，该健康指标即可量化设备的健康状态。HMM通常根据设备健康指标将设备健康状态分为特定等级，然后将评估得到的设备健康指标映射到特定等级。

(2)HMM构建

通过对设备健康指标进行数据处理、分类、抽样后，得到算法的输入数据。将该数据输入本文所提的双重EM算法可得构建Age-dependent HMM所需的参数A0和δ，并构建新的HMM。

(3)设备状态评估

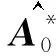
根据式(5)，t(k)=kΔt时前向变量αt(k)(i)和后向变量βt(k)(i)可以表示为

(25)

式中：1≤k≤f，1≤i≤N。

根据αt(k)(i)和βt(k)(i)，可以得到设备在t(k)=kΔt时处于状态i的概率

(26)

根据最大后验估计方法，t(k)=kΔt时设备所处的状态

3 算例分析

本文以一钻孔加工设备为研究对象，该设备主要对金属材料小型板件进行钻孔加工。根据工程师的工作经验，该设备的主轴电压信号能较好地反映设备性能的优劣，主轴电压信号可通过电压信号传感器采集得到。在实际加工过程中，当设备处于更好的健康状态时，其性能较优，磨损较小，相应的负载也较小，采集的主轴电压信号样本特征振幅更小；相反，当设备处于更差的健康状态时，其性能较差；磨损较大，相应的负载也较大，采集的主轴电压信号样本特征振幅更大。

(1)数据收集与处理

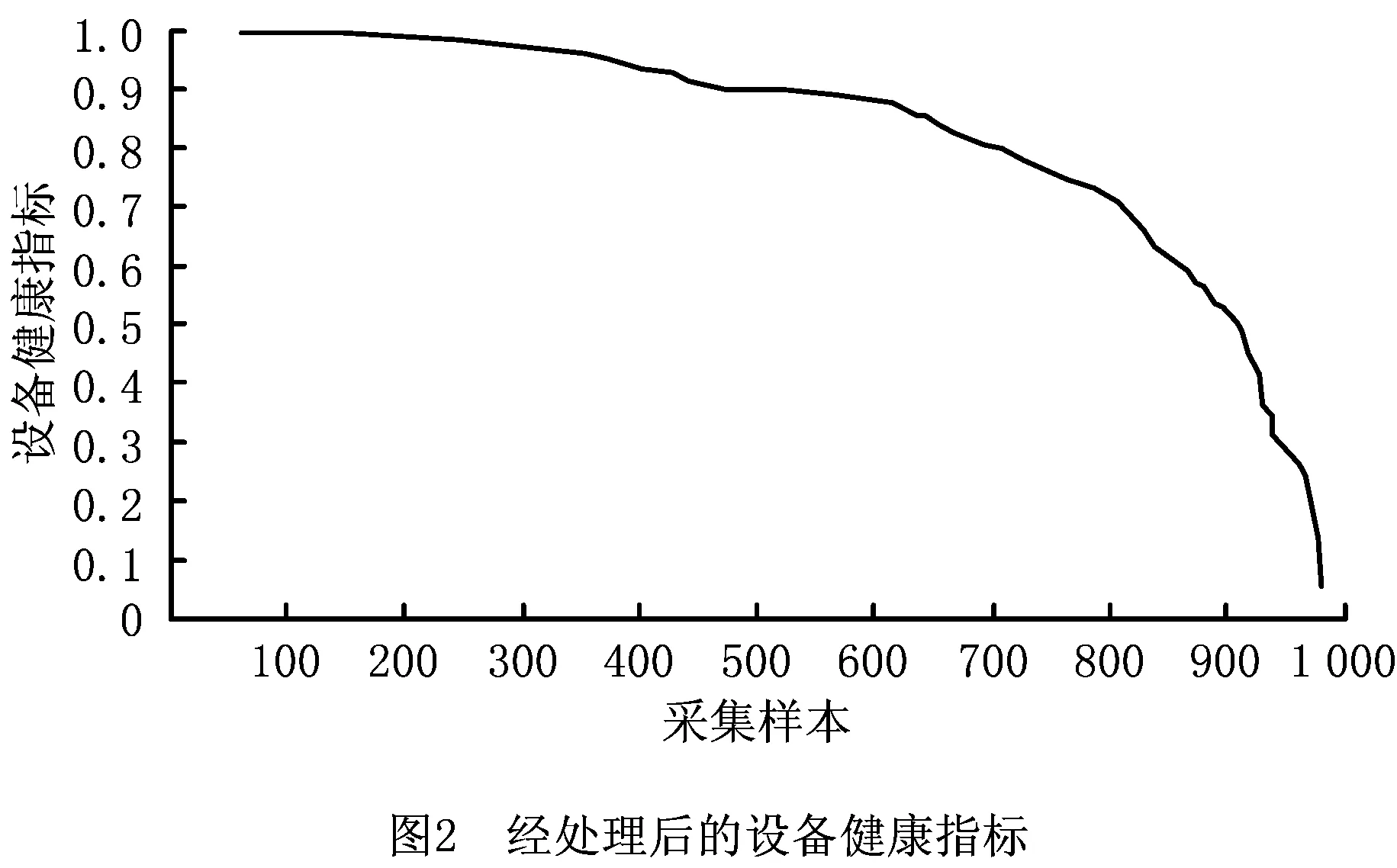
本文所提模型必须配备适量的训练数据才能较好地模拟设备状态的劣化情况。该钻孔加工设备用主轴电压信号反映其设备性能的优劣，即收集980个反映设备性能变化过程的主轴电压信号，进行数据预处理、特征提取和降维等处理[25]后，用于估计设备健康状态，可得到各样本数据对应的设备健康指标，如图2所示。

本文采用交叉检验[26]的方法选择最优的等级划分。基于现有数据可确定不同等级数目下HMM诊断结果的错误率，由此得到状态数目和诊断错误率的关系(如图3)，进而确定N=5时的HMM可用于后续的设备状态评估。同理，通过该交叉验证思想可进一步确定设备健康状态和健康指标值的对应关系。

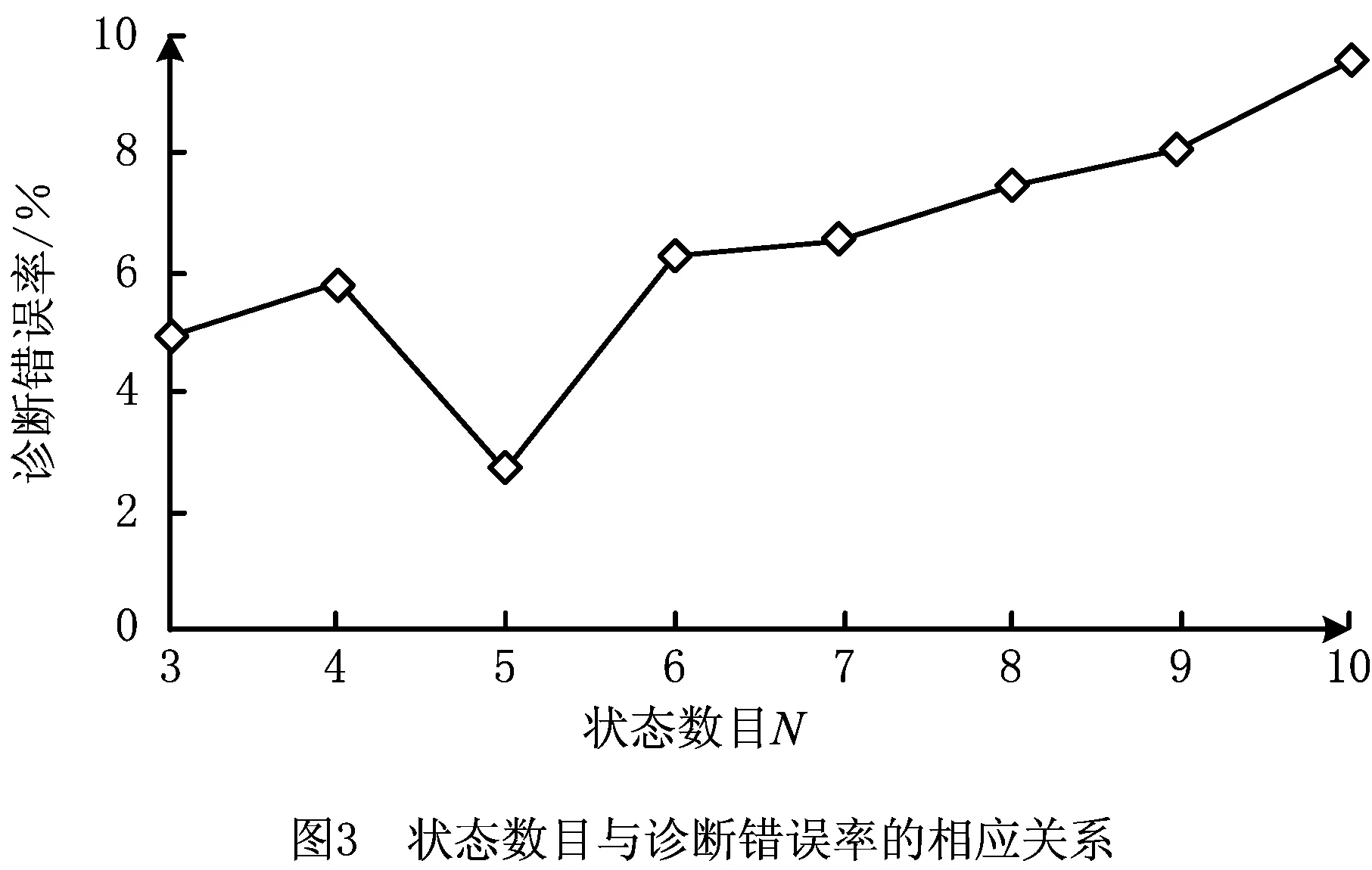
因此，本文将设备健康状态划分为五级，如表1所示，其中“1”表示设备处于最好状态，“5”表示设备处于最差状态(即设备已失效)。根据表1的设备健康状态分级方式，将处理后的设备指标数据转化为可用于本文计算输入的设备状态劣化序列。

表1 健康状态分级

通过上述设备健康状态分级方式，对收集的12组设备性能变化实时数据序列进行转化，得到12组设备状态劣化序列，其中一组设备劣化序列(含38个观测数据)如图4所示。

(2)HMM构建

根据输入的12组设备劣化观测序列，采用K-means聚类算法估算出AI0，有

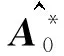
(3)状态评估

本文采用另一组包括40个数据的验证序列来验证模型的有效性，评估结果如表2所示。

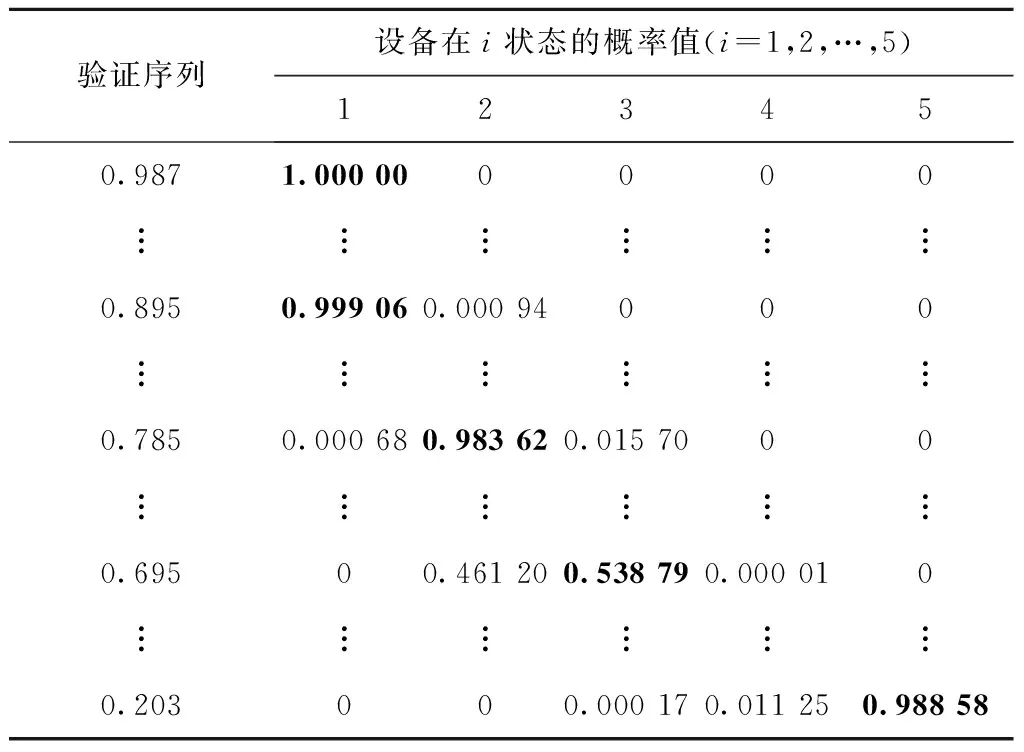
表2 评估结果

本文还利用该数据对传统HMM(其参数λ用Baum-Welch算法[27]得到)进行训练，并用训练后的模型进行评估。表3对比了两类方法得到的评估结果。可见，本文提出的Age-dependent HMM准确率更高，显示了其良好的评估性能。

表3 评估结果对比

注：正确为1，错误为0。

4 结束语

设备维护管理对于设备正常运行和企业顺利生产意义重大，而准确的设备状态评估是进行设备维护管理的前提。虽然HMM已广泛用于设备状态评估并取得了一些成果，但是基于传统HMM的设备状态评估却仍有一定不足，其假定设备各个状态间的转移概率为固定值，忽略了劣化过程中设备转移到更差状态的概率会增大、保持原有较好状态的概率会减小的实际情况，使HMM无法有效地模拟设备劣化过程并准确评估设备状态。

为提高设备状态评估的准确率，本文提出一个Age-dependent HMM，该模型通过引入劣化因子来克服传统HMM的转移概率为固定值而不能准确反映设备实际劣化过程的不足。同时，由于在HMM中引入了新因素，为合理构建改进的HMM，本文还开发了一个双重EM算法来估计设备初始状态转移概率A0和δ，并基于所提出的改进HMM，通过最大后验估计的方法来评估设备在各观测时刻的健康状态。最后的算例分析结果证明了本文所提模型的有效性和准确性，为完善现有设备状态评估研究提供了一定的支持。

结合本文结果，下一步研究可针对EM算法对初值敏感的不足进行改进。另外，还将继续探讨劣化因子的其他设计方式，优化Age-dependentHMM，使其更加满足实际生产的需要。

参考文献:

[1] DENG Chao, SUN Yaozong, LI Rong, et al. Hidden markov model based on the heavy-duty CNC health state estimate[J]. Computer Integrated Manufacturing Systems,2013,19(3):552-558(in Chinese).[邓 超,孙耀宗,李 嵘,等.基于隐Markov模型的重型数控机床健康状态评估[J].计算机集成制造系统,2013,19(3):552-558.]

[2] XIA Lisha. Research on fault diagnosis and related algorithm based on hidden Markov model[D]. Wuhan:Huazhong University of Science and Technology,2014(in Chinese).[夏丽莎.复杂条件下基于HMM的故障诊断技术研究[D].武汉：华中科技大学,2014.]

[3] BUNKS C, MCCARTHY D, AI-ANI T. Condition-based maintenance of machines using hidden Markov models[J]. Mechanical Systems and Signal Processing,2000,14(4):597-612.

[4] ATLAS L, OSTENDOR M, BERNARD G D. Hidden Markov models for monitoring machine tool-wear[C]∥Proceedings of the IEEE International Conference on Acoustic, Speech, and Signal Processing.Washington,D.C.,USA:IEEE,2000:3887-3890.

[5] ERTUNC H M, LOPARO K A. A decision fusion algorithm for tool wear condition monitoring in drilling[J]. International Journal of Machine Tools and Manufacture,2001,41(9):1347-1362.

[6] DONG Ming, HE D. A segmental hidden semi-Markov model(HSMM)based diagnostics and prognostics framework and methodology[J]. Mechanical Systems and Signal Processing,2007,21(5):2248-2266.

[7] DONG Ming, HE D. Hidden semi-Markov model-based methodology for multi-sensor equipment health diagnosis and prognosis[J]. European Journal of Operational Research,2007,178(3):858-878.

[8] DONG Ming, PENG Ying. Equipment PHM using non-stationary segmental hidden semi-Markov model[J]. Robotics and Computer-Integrated Manufacturing,2011,27(3):581-590.

[9] WU X, LI Y, TENG W. Modified hidden semi-Markov models for motor wear prognosis[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part J Journal of Engineering Tribology,2015,226(2):174-179.

[10] ZHU Kunpeng, LIU Tongshun. On-line tool wear monitoring via hidden semi-Markov model with dependent durations[J]. IEEE Transactions on Industrial Informatics,2017,14(1):69-78.

[11] LIU Qinming, DONG Ming, LYU Wenyuan, et al. A novel method using adaptive hidden semi-Markov model for multi-sensor monitoring equipment health prognosis[J]. Mechanical Systems and Signal Processing,2015,64(12):217-232.

[12] GONG Xun, FENG Yixiong, TAN Jianrong, et al. Fault diagnosis based on spatial structure hidden Markov model[J]. Computer Integrated Manufacturing Systems,2012,18(1):132-139(in Chinese).[龚 勋,冯毅雄,谭建荣,等.基于空间结构隐Markov模型的故障诊断[J].计算机集成制造系统,2012,18(1):132-139.]

[13] XIA Lisha, FANG Huajing, ZHANG Hui. HMM based modeling and health condition assessment for degradation process[C]//Proceedings of the 25th Chinese Control and Decision Conference. Washington, D.C., USA: IEEE,2013:2945-2948.

[14] LIAO Wenzhu , LI Dan , CUI Shihao. A heuristic optimization algorithm for HMM based on SA and EM in machinery diagnosis [J]. Journal of Intelligent Manufacturing, 2016:1-13. DOI: 10.1007/s10845-016-1222-1.

[15] LE T T, CHATELAIN F, BERENGUER C. Hidden Markov models for diagnostics and prognostics of systems under multiple deterioration modes [C]//Proceedings of Conference on European Safety and Reliability. Boca Raton, Fla., USA: Taylor & Francis-CRC Press/Balkema, 2014, 230(5): 473-484.

[16] YUWONO M, QIN Yong, ZHOU Jing, et al. Automatic bearing fault diagnosis using particle swarm clustering and Hidden Markov model[J]. Engineering Applications of Artificial Intelligence,2016,47(C):88-100.

[17] GAO Yinqiang, XIE Nan, HU Kai, et al. An optimized clustering approach using simulated annealing algorithm with HMM coordination for rolling elements bearings’ diagnosis[J]. Journal of Failure Analysis & Prevention,2017,17(3):1-18.

[18] LI Ling, CHENG Guoqing, LIU Bingxiang. Accelerated deterioration system model based on Gamma process and its optimal condition-based maintenance policy[J]. Computer Integrated Manufacturing Systems,2013,19(11):2922-2927(in Chinese).[李 玲,成国庆,柳炳祥.基于Gamma过程的加速劣化系统模型及其最优视情维修策略[J].计算机集成制造系统,2013,19(11):2922-2927.]

[19] PENG Ying, DONG Ming. A prognosis method using age-dependent hidden semi-Markov model for equipment health prediction[J]. Expert Systems with Applications,2011,38(10):12946-12953.

[20] PENG Ying. A prognosis method using age-dependent hidden semi-Markov model and a systematic maintenance policy[D]. Shanghai:Shanghai Jiao Tong University,2011(in Chinese).[彭 颖.基于退化隐式半马尔科夫模型的设备健康预测及系统性维护策略研究[D].上海：上海交通大学,2011.]

[21] PENG Ying, DONG Ming. A hybrid approach of HMM and grey model for age-dependent health prediction of engineering assets[J]. Mechanical Systems and Signal Processing 2011, 25(1):237-252.

[22] ARGON C, WU G S. Real-time health prognosis and dynamic preventive maintenance policy for equipment under aging Markovian deterioration[J]. International Journal of Production Research,2007,45(15):3351-3379.

[23] WANG Mei, WANG Jie. CHMM for tool condition monitoring and remaining useful life prediction[J]. International Journal of Advanced Manufacturing Technology,2012,59(5/6/7/8):463-471.

[24] SIOHAN O, CHESTA C, LEE C H. Joint maximum a posteriori adaptation of transformation and HMM parameters[J]. IEEE Transaction on Speech and Audio Processing, 2001, 9(4):417-428.

[25] LIAO Wenzhu. Research of predictive maintenance policy and integrated production scheduling model based on machine degradation[D].Shanghai:Shanghai Jiao Tong University,2011(in Chinese).[廖雯竹.基于设备衰退机制的预知性维护策略及生产排程集成研究[D]. 上海:上海交通大学, 2011.]

[26] GILLES C, JEAN B D. Selecting hidden Markov model state number with cross-validated likelihood[J]. Computational Statistics,2008,23(4):541- 564.

[27] WELCH, LIOYD R. Hidden Markov models and the baum-welch algorithm[J]. IEEE Information Theory Society Newsletter,2003,53(2):194-211.