McKibben型气动人工肌肉研究进展与趋势

谢胜龙,梅江平,刘海涛

(天津大学 机构理论与装备设计教育部重点实验室,天津 300072)

1 问题的提出

气动人工肌肉(Pneumatic Artificial Muscle, PAM)又称为气动肌肉执行器(Pneumatic Muscle Actuator, PMA)，因其具有结构简单、重量轻、输出力/自重比大、柔性大等优点[1]，越来越受到工业界的青睐，其中应用最广泛的是MicKibben型气动人工肌肉[2](如图1，以下简称为气动人工肌肉)。由于气动人工肌肉的结构特点，使其具有以下固有特性：

(1)因编织网之间、编织网与橡胶管之间的摩擦，以及橡胶管的拉伸与变形，导致的迟滞现象(hysteresis)[3]。

(2)由橡胶管与编织网之间的间隙与摩擦产生的门槛气压[4](threshold pressure)效应。

(3)气动人工肌肉橡胶管在充放气过程中产生的周期性松弛[5]，以及因气动人工肌肉内部摩擦产生温升[6-7]而引起的蠕变[5](creep)或漂移[8](drift)现象。

(4)由气体的可压缩性和橡胶管的柔性导致的柔顺性[9-10](compliance)。

(5)行程受负载影响[11-12]，其气压位移迟滞特性亦随负载变化[13]。

(6)闭环带宽(bandwidth)低[14]，限制了气动人工肌肉的伸缩频率[15]。

气动人工肌肉因上述特性而呈现出强非线性与时变性，极大地增加了控制系统的复杂程度。为了更好地将气动人工肌肉应用到实际工程中，国内外学者针对上述问题从气动人工肌肉的静/动态特性建模、迟滞特性建模、控制策略等方面进行了大量研究，取得了诸多成果[16-17]。

本文对气动人工肌肉的相关理论研究进行了系统整理和分析，回顾了气动人工肌肉建模和控制方法的发展历程，总结了国内外相关机构的研究进展，归纳了在静/动态特性建模、迟滞特性建模与参数辨识及控制策略等方面的研究现状和最新成果，并在此基础上展望未来研究发展方向。

2 气动人工肌肉建模方法

研究气动人工肌肉的基本特性与相应的参数建模方法，是实现其控制与应用的前提和基础[18]。为研究气动人工肌肉的工作特性和控制器设计方法，需首先建立其数学模型，进而分析系统参数对控制性能的影响[19]。回顾现有文献，可将气动人工肌肉的参数模型分为静态特性模型和动态特性模型两类。

2.1 静态特性建模方法

气动人工肌肉的静态特性模型反映的是气动人工肌肉的拉力与气压和长度之间的函数关系[20]。在大量文献调研工作的基础上，本文将气动人工肌肉的静态特性模型划分为几何模型、现象模型、实验模型和有限元模型。

2.1.1 几何模型

几何模型的建模方法分为两种[21]：①能量法，即基于虚功原理建立气动人工肌肉的静态模型；②力平衡法，即通过横截面的轴向和周向力平衡条件建立气动人工肌肉的静态模型。表面气压力剖面法[22-23](force profile of the surface pressure)归于力平衡法。

基于虚功原理建立的气动人工肌肉几何模型有Gaylord模型、Schulte模型、Chou模型和Tondu模型。1958年，Gaylord[24]在忽略乳胶管弹性、迟滞和端部非圆柱体影响的情况下，首次建立了气动人工肌肉拉力与气压和长度的几何关系

(1)

式中:F为拉力；P为气动人工肌肉容腔内的绝对充气压力；φ为外部编织网的编织角；D45°为编织角45°时气动人工肌肉的直径。

在基于气动人工肌肉为理想圆柱体的假设下，Schulte[25]于1961年建立了气动人工肌肉的几何模型;Chou等[26]以气压P和编织角θ为参数，根据能量守恒原理提出气动人工肌肉静态模型，其结果与Gayloard模型一致；Tondu等[27]以气压P和收缩率ε为参数，利用虚功原理得到气动人工肌肉静态模型

(2)

(3)

式中：r0和L0分别为气动人工肌肉在初始状态下的半径和长度；ε为收缩率；L为气动人工肌肉充气收缩后的长度；α为编织角。式(2)表明气动人工肌肉的拉力与气压成正比，与收缩率成非线性关系。实际上，该式与Gaylord模型式(1)等价，但因为收缩率ε比编织角θ更易于通过实验测得，所以实际应用中多采用Tondu公式或其修正公式[28]。

以上经典模型在建模时均基于以下假设条件：①忽略橡胶管的弹性；②忽略橡胶管的壁厚；③忽略气动人工肌肉端部效应(假设其工作容腔为理想圆柱体)；④忽略橡胶管与纤维编织网之间的摩擦力。因此，这类模型又被称为气动人工肌肉理想几何模型。事实上，气动人工肌肉在充气过程中，橡胶管会将一部分压缩气体的能量储存为橡胶管的弹性应变能，通过橡胶管的弹性力表现出来。当气动人工肌肉变形较大时，橡胶管的弹性力不可忽视。因此，上述模型虽然能够反映气动人工肌肉的拉力与气压和长度之间的关系，但由于在建模中忽略了橡胶管的弹性、壁厚及橡胶管与纤维编织网之间的摩擦力作用，且未考虑气动人工肌肉两端的变形，导致模型存在约15%的偏差[29]。此外，上述模型在低压下的精度并不理想，这是因为在低压条件下，橡胶管的弹性以及橡胶管与纤维编织网间的摩擦力和间隙引起的门槛气压效应不可忽略。

考虑气动人工肌肉两端为非理想圆柱体这一因素，Tondu在其模型中引入了实验常数k，即

(4)

(5)

针对理想几何模型在低压下精度低的问题，假定k=ake-p+bk，其中ak和bk通过实验数据辨识得到，从而得出与实际更为接近的数学模型。

基于力平衡法建立的气动人工肌肉几何模型包括Ferraresi模型和CaldWell模型。2001年，Ferraresi等[30]首次提出气动人工肌肉的力平衡模型，通过轴向和周向的力平衡条件建立了气动人工肌肉的静力学模型。该模型虽然考虑了几何约束和橡胶管弹性，但是仍假设气动人工肌肉为理想圆柱体。研究结果发现，不论基于能量方法还是基于力平衡方法，所得到的参数模型均包括Gaylord模型中的原始几何力项。在此基础上，Kothera等[31]考虑橡胶管厚度，通过引入材料的弹性模量E提出了改进模型，显著地提高了模型精度。需要指出的是，虽然改进模型与实验数据吻合较好，但对于商用气动人工肌肉，弹性模量E不易获取，因此该模型缺乏通用性。Davis等[32]随后提出一种分析建模方法，即基于表面气压力的剖面法。结果发现，不论考虑壁厚与否，所得到的气动人工肌肉力平衡方程与Chou模型一致。为了获得更高的模型精度，Davis在此基础上考虑了气动人工肌肉两端端盖表面积/直径对气动人工肌肉模型/输出力的影响，结果发现，所建模型在中间压缩段的精度非常高，虽然在完全膨胀时误差会增加约8%～10%，但是精度仍比理想模型高30%～50%。随后，Davis等[33]试图利用干摩擦模型描述气动人工肌肉的迟滞特性以提高模型精度，但因引入了许多难以量化的参数而增加了模型的复杂性。

综上所述，最初的气动人工肌肉建模方法均基于几何约束，利用参数间的几何关系建立数学模型，其缺点是模型中的参数只能在静态条件下得到，在气动人工肌肉伸缩过程中不宜测得，因此几何模型无法描述气动人工肌肉的动态特性[34]。

2.1.2 现象模型

为预测气动人工肌肉拉力、长度和速度之间的关系，学者们受骨骼肌现象模型的启发，借鉴Hill模型[35]，提出气动人工肌肉的现象模型[36]。现象模型的研究分为两种：①由Colbrunn等[37-38]提出的将气动人工肌肉视为弹簧单元、粘性阻尼单元和库伦摩擦单元构成的并联系统；②由Reynolds等[39-40]提出的将气动人工肌肉视为弹簧单元、阻尼单元和收缩力单元构成的并联系统。上述两种模型分别称为Colbrunn现象模型和Reynolds现象模型(也称为三元素模型)。

在Colbrunn模型(如图2)中，弹簧单元用于描述非线性力—长度关系，粘性阻尼单元用于描述系统的气流能量损失，库伦摩擦单元用于描述内部橡胶管与外部编织网套之间摩擦力造成的能量损失。其中，非线性的力—长度关系为

Fn=

(6)

(7)

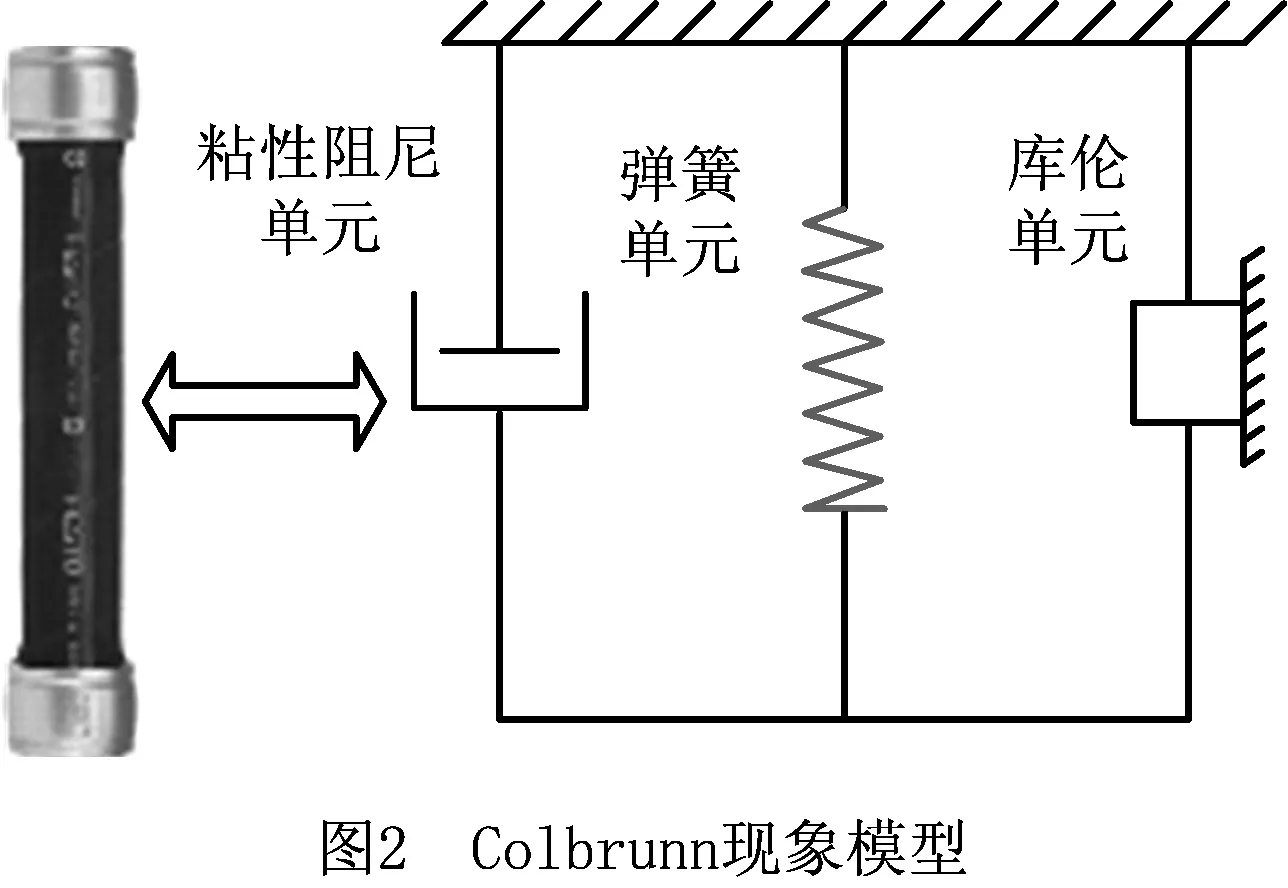
式中:Pg为气动人工肌肉内部气压；L为气动人工肌肉长度；b为单根纤维长度；n为单根纤维缠绕圈数；Kbraid为编织网材料的刚度；Lmin和Lmax分别为和气动人工肌肉收缩的最小长度和原长；Fmaxlimit为气动人工肌肉编织网材料产生的刚性力。系统动力学模型为

(8)

(9)

式中：v为执行器末端速度；k为执行器线性化刚度；c为粘性阻尼系数；Q=μN/k为库伦阻尼常数。阻尼常数c和Q均由实验测得。

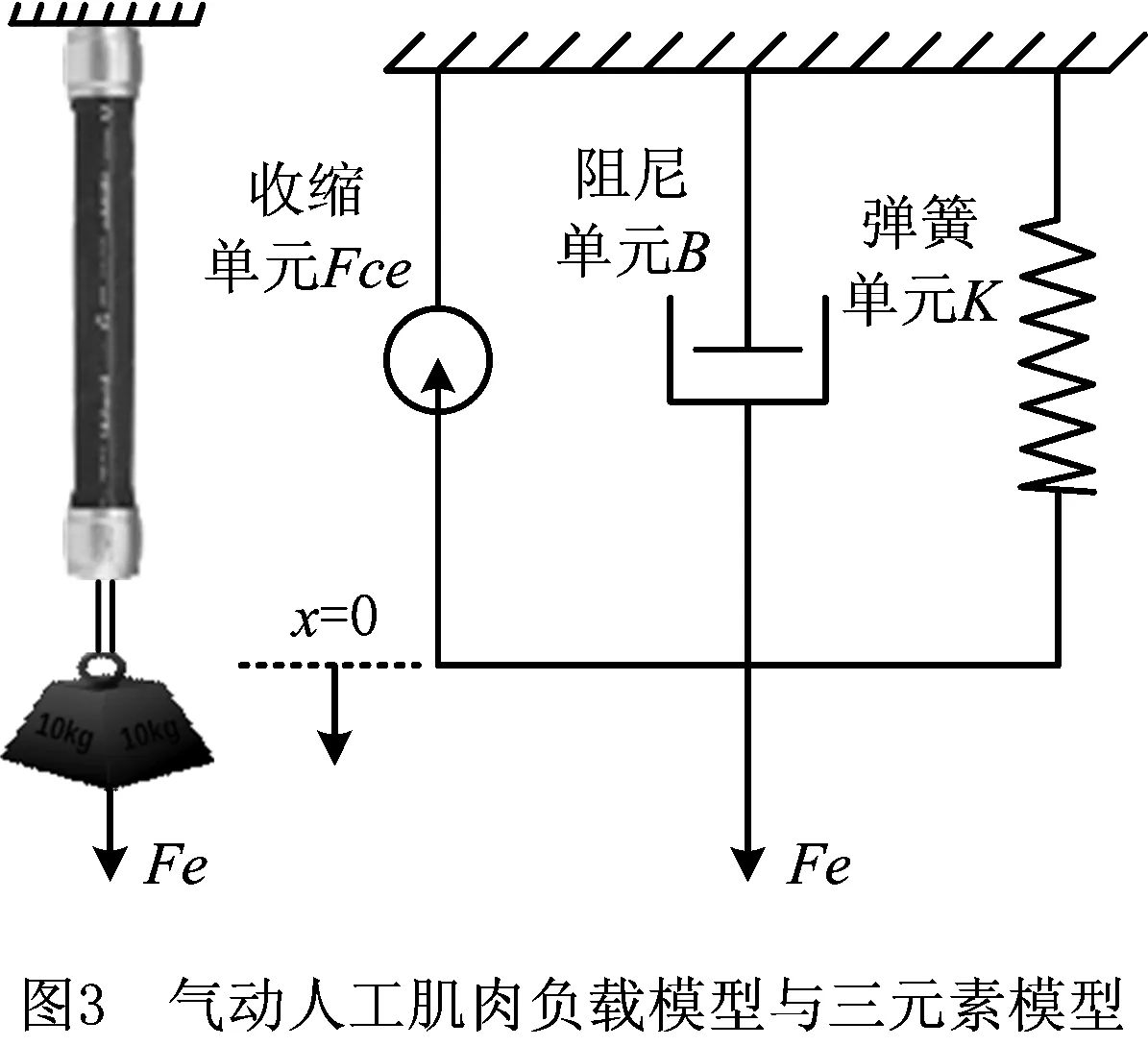
Reynolds在Repperger[41-42]提出的两元素模型的基础上进行了改进，提出采用收缩单元、弹簧单元和阻尼单元并联组成的三元素模型(如图3)，并通过实验获得了气动人工肌肉充气压力在207 kPa～621 kPa范围内的模型参数。实验结果表明，三元素模型在低压和高压下均具有良好的精度。三元素模型公式及其带负载动力学方程如下：

FTotal=FSteady-state+FTransient-Fce

(10)

K(x)=a2x2+a1x+a0;

(11)

(12)

(13)

式中:x为气动人工肌肉移动位移；K为弹簧刚度；B为阻尼系数；ai,bi均为实验拟合数据；FTotal为气动人工肌肉产生的拉力；FSteady-state为气动人工肌肉弹簧单元产生的收缩力；FTransient为气动人工肌肉阻尼单元产生的收缩力；Fce为气动人工肌肉收缩单元产生的收缩力，由实验测得；Fe为负载。

需要指出的是，因为现象模型采用粘性阻尼单元或库伦单元描述气动人工肌肉中的摩擦效应，所以无法准确描述因动态摩擦产生的迟滞和蠕变等非线性现象。鉴于现象模型的控制方案中不能采用摩擦补偿控制策略，为在气动人工肌肉控制中考虑迟滞、时变等非线性因素，需采用高级控制策略或智能控制策略。

2.1.3 实验模型

由于气动人工肌肉某些内部结构参数的数值难以准确获取，且气动人工肌肉几何模型在低压下的精度较差[43]，一些学者尝试通过实验方法建立了气动人工肌肉的静态特性模型，即利用实验数据拟合气动人工肌肉收缩力与其内部气压及位移之间的函数关系。

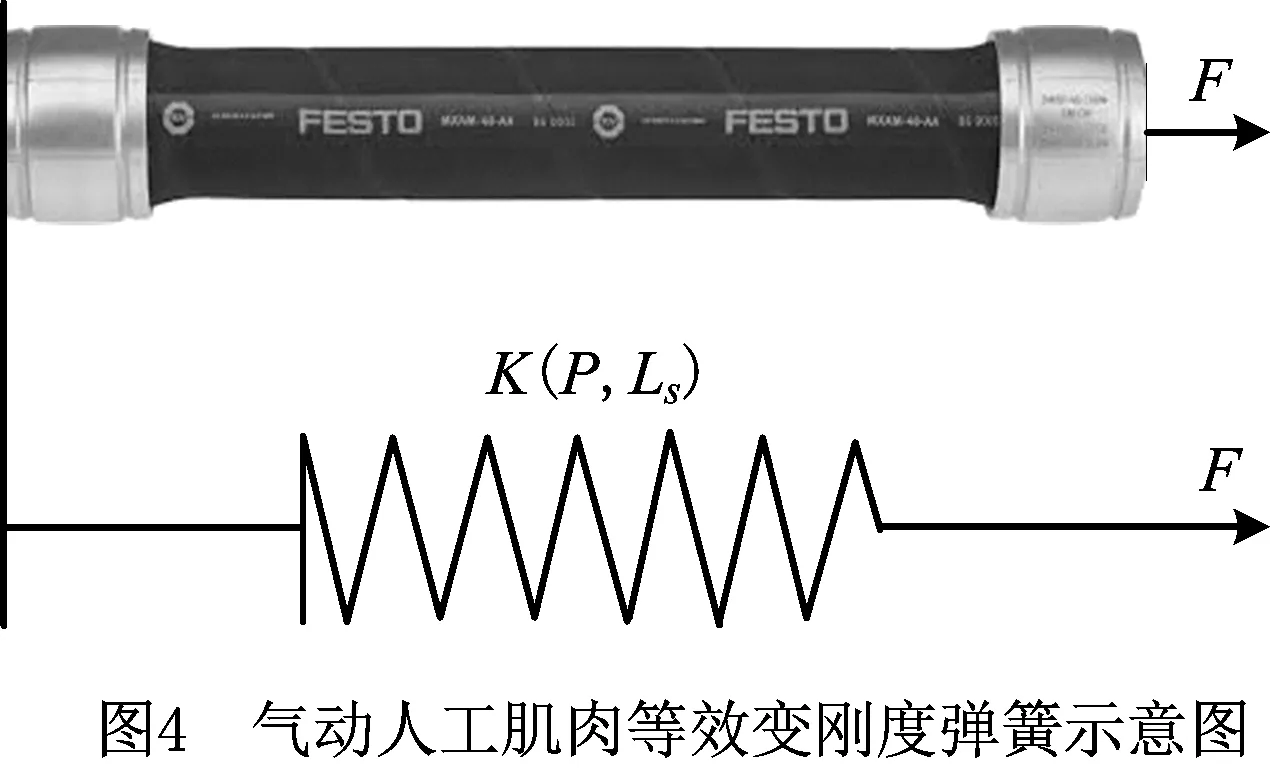
从实验观察的结果来看，作用在气动人工肌肉上的拉力与作用在弹簧上的拉力等效，是长度的函数，不同的是气动人工肌肉的拉力还与气压有关。受此启发，Wickramatunge等[44-45]将气动人工肌肉等效为变刚度弹簧(如图4)，将其刚度K视为气压P和工作长度Ls的函数，并采用二阶多项式拟合刚度K。

Felastic=K(P,Ls)Ls;

(14)

(15)

式中a0，a1，a2和a3为常数，通过实验数据采用最小二乘法获得。实验发现，当给定气压时，拉伸长度增加则刚度值增加；但当给定拉伸长度时，若气压小于某个气压值，则刚度随气压的增加而减小，若气压大于该气压值，则刚度随气压的增加而增加。对于该现象，Wickramatunge认为低压时乳胶管的弹性变形是影响气动人工肌肉拉力的主要因素。

受气动人工肌肉的拉力与气压成正比，而与收缩率成非线性关系的启发，Petrovic[46]选择了关于位移的二阶多项式来建立气动人工肌肉的静态模型。然而，该模型无法表示拉力为0时，气压和位移之间的函数关系。为解决这一问题，Pujana-Arrese[47]在上述模型中添加了仅依赖于位移的修正项，该修正项易由实验辨识得到[48]。气动人工肌肉的拉力表达式为

F=(D1+D2q+D3q2)P+φ(q);

(16)

φ(q)=a1+a2q+a3q2+a4q3+a5q4。

(17)

式中:q为气动人工肌肉的位移；P为气动人工肌肉的内部气压；D1，D2和D3为待拟合参数；φ(q)为关于气动人工肌肉位移的4阶多项式；a1，a2，a3，a4和a5为待拟合参数。

2.1.4 有限元模型

Bertetto等[49]采用有限元方法分析研究了McKibben和直纤维式(straight fiber)气动人工肌肉。仿真结果表明，两种气动人工肌肉的变形和拉力与实验结果吻合。Shan等[50]采用大变形膜理论和层叠增强型纤维复合材料的大变形理论建立了气动人工肌肉的非线性有限元模型，通过编写数值仿真程序，预测了气动人工肌肉在高强度轴向力下的特性，并进行了实验验证，结果说明两者吻合较好。国内学者臧克江[51]利用有限元软件ABAQUS对气动人工肌肉进行了几何建模，并进行了等压、等长和等载特性模拟和静态特性实验验证，取得了良好的效果。Nozaki等[52-53]采用有限元方法进行了气动人工肌肉的运动分析，结果发现在计及橡胶管与编织网间摩擦后，气动人工肌肉的特性可被准确预估，该结论有助于气动人工肌肉的设计。

然而，由于气动人工肌肉有限元建模方法过程复杂、计算量大，不适用于气动人工肌肉控制，而常用于辅助气动人工肌肉的结构优化设计和理论验证。

为了直观地展示气动人工肌肉静态特性建模的发展历程，图5给出了各模型所处的时间段。从图中可以看出，由于气动人工肌肉几何模型的缺陷，其静态特性建模正逐渐朝着实验模型的趋势发展。

2.2 动态特性建模方法

决定气动元件驱动力的关键因素是其内部压力和作用面积。对于气动人工肌肉而言，其驱动面积由柔性结构的编织网和橡胶管共同决定[54]。在气压传动系统中，气动人工肌肉为一种气动执行元件，充放气过程中压缩空气的流动及流动中的热力学过程对整个系统的影响不可忽略[55]，不能简单地将其视为执行元件，而必须考虑其在充放气过程中的动态特性。气动人工肌肉动态特性指其充放气特性，反映的是气动人工肌肉伸缩过程中气压与体积和流量之间的动态变化关系，其动态特性方程是控制系统数学模型中的关键部分。

2.2.1 变截面气缸法

华中科技大学的杨钢等[56-57]在推导气动人工肌肉动态特性方程时，将气动人工肌肉视为带弹性负载的变截面气缸，根据气缸的动态特性方程推导出气动人工肌肉的动态特性方程，并将气动人工肌肉的充放气动态过程分为等容充气、充气收缩、排气伸长、等容排气4个阶段，得到气动人工肌肉的动态特性方程

(18)

式中：k为气体绝热指数，k=1.4；R为气体常数，R=287.1 J/kg·K；P为气动人工肌肉腔室内的绝对压力；Qm1为进入气动人工肌肉腔室的气体质量流量；T为气体绝对温度；V为气动人工肌肉腔室工作容积。

将气动人工肌肉容腔视为理想圆柱体，则有

(19)

(21)

式中x为气动人工肌肉的收缩位移。

在充气状态下，气动人工肌肉的动态特性方程为

(22)

在放气状态下，气动人工肌肉的动态特性方程为

(23)

式中Qm2为气动人工肌肉腔室排向大气的气体质量流量。由式(22)和式(23)可见，所得到的动态方程与气缸的动态特性方程相似，只是气缸活塞工作面积为定值，而气动人工肌肉的等效工作面积随位移变化。

2.2.2 理想气体多变方程

气动人工肌肉的橡胶管由弹性尼龙材料构成，且在其伸缩过程中的热量损耗极少，可将其伸缩过程视为等温(isothermal)和绝热(adiabatic)过程。因此，气动人工肌肉体积与内部气压之间的关系可由理想气体多变方程(polytropic equation，polytropic gas law)确定[58-59]：

(24)

对式(24)全微分可得

(25)

即

(26)

由理想气体状态方程有

PV=mRT。

(27)

带入式(27)得

(28)

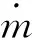
由于气动人工肌肉的体积V在伸缩过程中不断变化，可将其视为伸缩率的函数[60]:

(29)

式中Cn为多项式函数的系数。

上述两种方法虽然推导思路和得到的方程形式不同，但最终结果是等价的，二者区别在于：前者认为气动人工肌肉为理想圆柱体，后者则考虑了气动人工肌肉端部非圆柱效应。由动态特性方程(22)，(23)和(28)可知，气体质量流量与气压成正比关系，而与位移成非线性关系。

3 气动人工肌肉的迟滞特性

3.1 气动人工肌肉的迟滞

关于迟滞，至今尚未有统一的定义，有关迟滞的详细论述请参见文献[61]。迟滞可理解为同一个输入量对应的正反行程输出量不一致的现象。对于气动人工肌肉可理解为，在气动人工肌肉运动过程中，同一位置(或伸缩率)所对应的气压/力因其伸缩状态的不同而不同(参见文献[13]中Fig.7)。文献[62]最早发现了气动人工肌肉的迟滞现象；Chou[20]在进行气动人工肌肉动力学测试时发现，气动人工肌肉的拉力与收缩率之间存在迟滞现象，并认为库伦摩擦是引起迟滞的主要原因；文献[3]认为迟滞现象由编织网之间的干摩擦、编织网和橡胶管之间的摩擦、橡胶管的弹性及其形状的改变引起，其中编织网之间的摩擦是最主要的因素。

气动人工肌肉的迟滞包括力位移迟滞和气压位移迟滞。气压位移迟滞可由等压实验得到，而力/长度迟滞必须通过等压实验和等长实验得到[63]。文献[59]介绍了力位移迟滞回线转换成气压位移迟滞回线的方法。因为在气动人工肌肉控制中，气压P是输入变量，所以实际应用中多使用气压位移迟滞回线。气动人工肌肉的迟滞现象具有两个特性[13，64]：①非局部记忆性(non-local memory characteristic)，指迟滞特性的输出信号不仅与当前的输入瞬时值有关，还与输入信号的历史极值有关；②准率不相关性(quasi rate-independent characteristic)，指气动人工肌肉伸缩频率对其力位移迟滞回线的影响几乎可以忽略不计。

3.2 迟滞特性建模方法

迟滞现象会引起能量损失并增加控制系统的复杂程度，但其在控制中又不可忽略。因此，许多摩擦建模方法被引入气动人工肌肉的摩擦建模中，以提高气动人工肌肉的动态响应精度。

需要注意的是，摩擦模型根据摩擦现象是否采用微分方程分为静态摩擦模型和动态摩擦模型[65]。静态摩擦模型将摩擦力表示为相对速度的函数；动态摩擦模型将摩擦力表示为相对速度和位移的函数，它既可以描述摩擦的静态特性，也可以描述其动态特性。迟滞现象是动态摩擦的一种特殊现象，学者们对于气动人工肌肉迟滞现象的研究经历了静态特性建模和迟滞建模两个阶段[63]。

为了解释迟滞现象，Chou等[26]在模型中添加了与气动人工肌肉伸缩方向相反的实验偏移力；Tondu等[27]在建模时添加了干摩擦模型以提高模型精度，但该模型建立仅考虑了编织网之间的干摩擦；Davis等[33]在Tondu模型的基础上考虑了编织网之间的接触面积对摩擦力的影响，但增加了模型的控制难度。在上述模型中，尽管通过引入摩擦模型对原有模型进行了修正，但所采用的摩擦模型均为静态摩擦模型——库伦摩擦，因此都无法准确描述闭环迟滞现象。为了准确描述气动人工肌肉的迟滞现象，Van Damme首次将Preisach模型应用于平板型气动人工肌肉[66]，此后Vo-Minh将Maxwell模型应用于MicKibben型气动人工肌肉，开启了气动人工肌肉迟滞建模的新篇章。对于迟滞模型，可根据迟滞回线的描述方法分为微分型迟滞模型和积分型迟滞模型[67]两类。

3.2.1 积分型迟滞模型

积分型迟滞模型又称算子型迟滞模型，该模型根据迟滞回线的逆转特性使用特定数目的迟滞算子拟合迟滞回线。积分型迟滞模型主要有Preisach模型、Krasnosel’skii-Pokrovs-kii(K-P)模型、Maxwell模型和Prandtl-Ishlinskii(PI)模型。

Kosaki等[68]和Schreiber等[69]分别使用Preisach模型作为迟滞补偿，并应用到反馈控制中，显著提高了轨迹控制精度；Minh[3，70]使用Maxwell模型拟合力位移迟滞回线，能够分析摩擦机理中的预滑动现象，并采用分段线性化方法(piecewise-linearization method)辨识Maxwell模型的参数。

3.2.2 微分型迟滞模型

微分型迟滞模型采用非线性微分方程描述迟滞的动力学特性。常见的微分型迟滞模型有Duhem模型、Dahl模型、LuGre模型和Bouc-Wen模型。

Zhao等[71]采用Duhem模型描述气动人工肌肉的迟滞现象，利用神经网络方法进行了参数辨识；金冠霖[72]采用LuGre摩擦模型建立了气动人工肌肉的迟滞模型，采用粒子群优化算法辨识了模型中的动态参数，并进行了实验验证；Aschemann等[73]采用广义Bouc-Wen模型描述力位移迟滞回线，并与准静态Maxwell模型和PI模型进行对比，表明采用广义Bouc-Wen模型作为迟滞补偿，能够使轨迹跟踪误差更小；Lin等[63]采用依赖于气压的迟滞建模方法推导了气动人工肌肉的迟滞模型，并与基于广义Bouc-Wen和PI模型的建模方法进行对比，表明PI模型和广义Bouc-Wen模型较Maxwell模型更真实地反映了气动人工肌肉的迟滞特性。

综上，微分型迟滞模型主要研究迟滞的非线性现象，该类模型结构复杂，参数较难确定，造成控制器设计中存在计算复杂、耗时、参数不易在线辨识和模型求解困难等问题，不利于进行高精度实时控制；而积分型迟滞模型通常采用迟滞单元加权叠加形式，其结构简单，仅需获取输入输出样本数据即可，因此控制策略易于实现。

4 气动人工肌肉控制策略

目前对气动人工肌肉控制方法的研究尚不成熟，主要原因是，气动人工肌肉内部多处摩擦产生的迟滞、门槛气压等非线性因素，容腔内气压波动产生的干扰，以及橡胶管周期性松弛产生的蠕变效应，使得气动人工肌肉成为一种多参数耦合、参数时变的非线性系统。常用的控制策略主要包括基于前馈迟滞补偿的控制策略、基于模型的高级控制策略和智能控制策略[74]。

4.1 前馈迟滞补偿控制策略

气动人工肌肉中因摩擦引起的迟滞、门槛气压及蠕变等现象严重影响了气动人工肌肉的控制精度，为实现其高精度的轨迹跟踪控制，必须对其迟滞进行补偿。图6所示为气动人工肌肉迟滞补偿控制的基本方案[63]：首先采用迟滞模型对获取的气动人工肌肉气压位移迟滞实验数据进行实验建模，然后采用最小二乘法等参数辨识方法对迟滞模型中的待辨识参数进行参数辨识，将获得的参数带入其逆模型中构建迟滞的前馈补偿器，将期望轨迹通过迟滞前馈补偿器转化为期望的控制气压，比例阀则根据期望的控制气压来控制气动人工肌肉内部的气压。由于气动人工肌肉在实际运动过程中不可避免地会存在各种干扰，为了提高控制系统的精度和鲁棒性，利用位移传感器实时采集气动人工肌肉的长度作为反馈信号与期望轨迹进行比较，然后通过PI控制修正控制变量，从而提高控制系统的精度。为了进一步提高系统的控制精度，可以采用图7所示的串级控制方案[59]，该控制方案将控制系统划分为内外两个控制环，外环反馈气动人工肌肉的轨迹，内环反馈气动人工肌肉的内部气压，位移传感器采集气动人工肌肉长度并反馈回去与期望轨迹比较修正控制变量ex，气压传感器采集的气动人工肌肉内部气压反馈回去与期望气压Pd比较后经过PI控制器转化为修正控制量eP来进一步提高控制系统的精度。

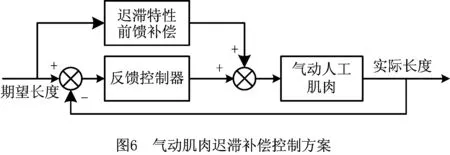
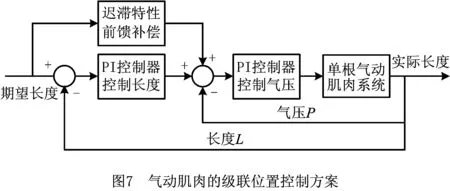
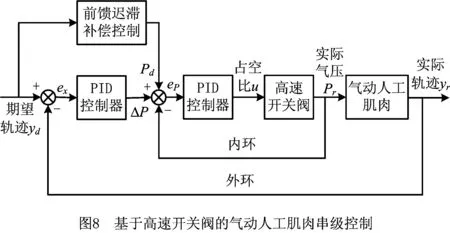
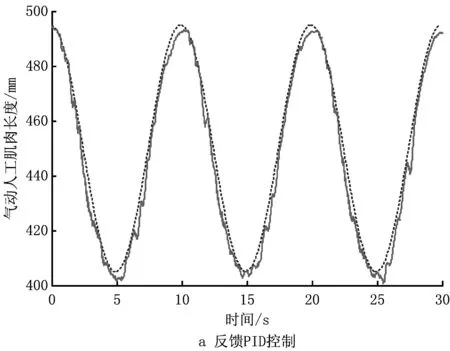
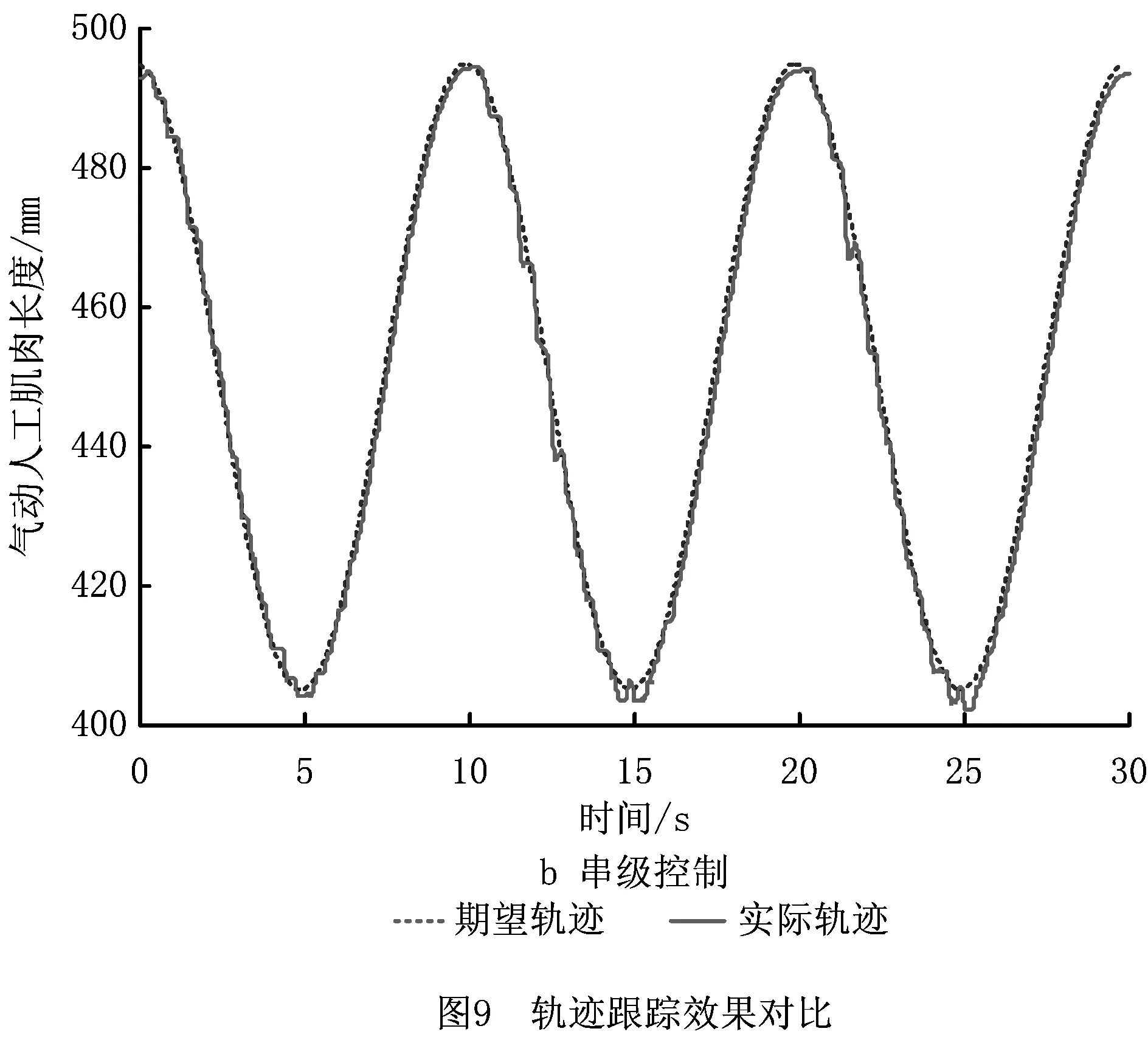
对于气动人工肌肉的位置控制而言，基于迟滞模型补偿控制策略的相关文献较少。Kimura等[75]在考虑气动人工肌肉迟滞特性的基础上，采用反馈线性化控制方法对气动人工肌肉系统实施控制，并通过实验验证了该方法的有效性。然而，该方法中的迟滞模型采用的是静摩擦模型，未完全反映气动人工肌肉的迟滞特性；Hildebrandt等[76]设计了一种级联控制方案，即内环用于力控制，以补偿系统非线性特性，外环用于位置控制，由基于摩擦模型的前馈补偿和基于反馈控制器的观测器组成，该方案极大地减小了稳态状态误差，但在负载阶跃变化时易产生震荡。在基于迟滞补偿控制方面做出较大贡献的当属Minh[13，59]。文献[13]采用Maxwell模型作为前馈补偿器，用以补偿气动人工肌肉的非线性特性，控制器为传统PI控制器，实验取得了良好的效果；文献[59]采用基于前馈迟滞模型补偿控制的串级控制策略(如图7)研究单根气动人工肌肉的轨迹跟踪控制，其中内环用于控制气动人工肌肉气压的非线性特性，外环用于控制气动人工肌肉动力学的非线性特性，使得气动人工肌肉具有良好的鲁棒性。受上述方法的启发，Xie等[77]采用修正PI模型建立了气动人工肌肉的气压位移迟滞模型，设计了一种基于高速开关阀控制的气动人工肌肉串级控制策略。图8所示为该控制方法的控制框图，图9所示为经典PID反馈控制和采用该方法的控制效果图，可见该方法在降低系统控制成本的同时显著提高了气动人工肌肉的轨迹跟踪控制精度。

4.2 高级控制策略

为降低气动人工肌肉迟滞、动态干扰(如气压波动)等因素给控制系统带来的复杂性与非线性，学者们引入了自适应控制、反馈线性化控制、滑模变结构控制和鲁棒控制等现代控制策略对气动人工肌肉的轨迹跟踪控制开展研究。这类方法的基本思想是将摩擦等非线性因素视为外部扰动，通过改变控制系统的结构或控制参数来提高系统抑制扰动的能力。显然，这类方法补偿的不仅是摩擦，还包括作用在系统上的其他扰动[78]。

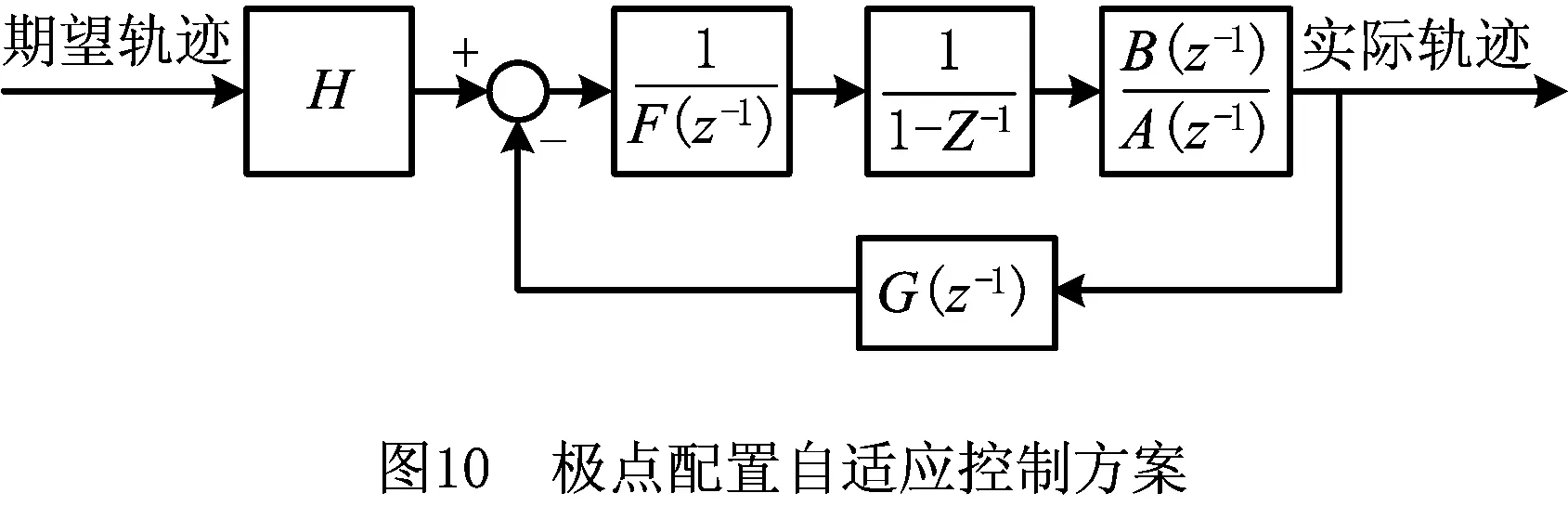
自适应控制由于可通过设计自适应律在线估计系统模型或控制器中的未知参数，有效处理系统未知动态对控制性能的影响而得到了广泛应用[79]。图10所示为气动人工肌肉的极点配置自适应控制方案图[80]，由于自适应控制对系统的阶数并不敏感，该方法采用低阶的自回归外生(AutoRegressive eXogenous，ARX)模型描述气动人工肌肉的受控过程，以此简化控制器的计算过程。该方法采用参数辨识的方法计算多项式A和B中的系数，从而得到所需的估计模型，具有直观、工程概念明显、鲁棒性强和适用范围广等优点。Caldwell等[14]首次采用极点配置自适应控制方法研究了由5根气动人工肌肉并联连接而成的机器人肘关节的控制；在此基础上，Ahn等[80]采用ARX模型描述由2根气动人工肌肉组成的拮抗式机械手的控制过程，并采用修正遗传算法在线辨识模型中的参数，取得了良好的控制效果。

反馈线性化的核心思想是将非线性系统部分或者全部转化为线性系统，以利用线性控制理论对受控系统进行控制，其与普通线性化的根本区别在于反馈线性化是通过状态变换和反馈得到，而不是通过系统的线性逼近得到[81]。Kimura等[75，82-83]采用库伦模型描述气动人工肌肉的力位移迟滞，在此基础上采用反馈线性化的方法研究了气动人工肌肉控制；Repperger等[41]基于两元素模型,采用反馈线性化的方法研究了气动人工肌肉的轨迹跟踪控制；Knestel等[84]采用多项式拟合方法拟合气动人工肌肉的力位移迟滞，并采用输入—输出线性化方法研究了一种康复机器人的轨迹跟踪控制；Alinia等[85]分别采用反馈线性化和模型参考自适应控制方法，对一种由3根气动人工肌肉驱动的并联平台的轨迹跟踪控制进行了仿真研究。

变结构控制方法的基本思想是，控制系统进入滑动模态后，其运动在一定条件下对外界干扰及参数的扰动具有很大鲁棒性，首先迫使受控系统的状态轨迹运动到事先选取的切换流形，然后控制系统状态沿着该切换流形渐进运动到系统的平衡点，即迫使受控系统按照控制率给定的滑动模态运动。因此，变结构控制的基本任务是设计合理的控制规律和选取适当的切换函数，使系统能够迅速到达指定的切换流形，并在系统进入滑动模态后具有良好的动态特性[86]。因为滑动模态可设计且与对象参数和扰动无关，所以这种控制方法具有响应快速、物理实现简单、抗干扰性能好等优点，适用于不确定性非线性控制系统[87]。Jouppila等[88]采用滑模变结构控制方法对基于高速开关阀驱动的气动人工肌肉控制系统进行了轨迹跟踪控制研究，并通过实验证明该方法具有较好的控制效果和良好的鲁棒性；在此基础上，Jouppila等[89]采用带积分项的二阶滑模面来提高轨迹跟踪精度，并通过变负载的轨迹跟踪实验表明该控制方法具有良好的鲁棒性；Shen[90]通过对气动人工肌肉运动过程中主要的非线性因素进行建模，建立了单根气动人工肌肉伺服系统的非线性动力学模型，并基于该模型采用滑模变结构控制方法研究了其轨迹跟踪控制；基于上述建模方法，Rahman[91]提出一种动态自适应反步滑模控制(Dynamical Adaptive Backstepping-Sliding Mode Control,DAB-SMC)策略，研究了由气动人工肌肉驱动的一种双向对拉式机构的轨迹跟踪控制，通过实验表明DAB-SMC控制方法比传统的变结构控制方法在精度上提高了33%；王斌锐等[92]针对一种由气动人工肌肉驱动的级联式肘关节设计了基于干扰观测器的滑模变结构控制算法，搭建了仿真和实验测试平台，并分别采用反馈PID、SMC和基于干扰观测器的滑模控制(Sliding Mode Control based on Disturbance Observer,SMC-DO)3种控制方法进行了比较研究，发现SMC-DO方法的误差更小、鲁棒性更好。

系统不确定性参数和各种外部干扰等不确定性因素会使系统的控制性能恶化。鲁棒控制就是设计一种控制器，使得系统存在一定程度的参数不确定性及一定限度的未建模动态时，闭环系统仍能保持稳定，并保持一定的动态性能品质[93]，它是一种在控制性能和鲁棒性之间进行的谨慎而合理的控制方法[94]。Lin等[95]基于三元素法建立的气动人工肌肉动力学模型，采用H∞鲁棒控制技术研究其轨迹跟踪控制，该控制方法对不同的轨迹均有良好的跟踪效果。为了保证控制系统鲁棒性的同时兼顾控制性能最优，Amato[96]基于保成本控制提出一种鲁棒最优控制用于气动人工肌肉驱动的机械臂轨迹跟踪控制，仿真说明效果良好。为了简单、高效地实现对由单根气动人工肌肉驱动的仿生关节的轨迹跟踪控制，王杨等[97]提出一种基于鲁棒建模方法的级联控制策略，该策略在工作频率相对较低的情况下能对气动人工肌肉实现有效的轨迹跟踪控制。

4.3 智能控制策略

上述控制策略均基于控制对象的数学模型，不仅精确建模非常困难，即使得到较为完善的模型，也会因其复杂的表达式而使分析和补偿难以实现。为解决模型非精确、非线性及参数时变等问题，学者们引入了智能控制理论，主要包括神经网络控制和模糊控制[98]。与传统控制方法[99]相比，智能控制方法不但不需要控制对象的数学模型，而且在处理复杂性和不确定性方面具有优势。

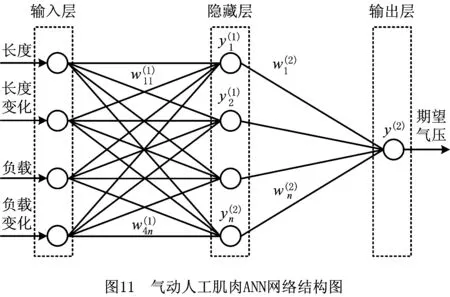
神经网络因为其学习能力可以不断修正神经元之间的连接权值，并离散存储在连接网络中，所以对非线性系统和难以建模的系统具有良好的映射能力，从而能够处理高维、非线性、强耦合和不确定性的复杂控制问题[100]。在神经网络控制方法中，所有的非线性特性由神经网络通过学习来补偿。图11所示为气动人工肌肉人工神经网络(Artificial Neural Network，ANN)结构图[101]，该神经网络中输入层为气动人工肌肉的长度、长度变化、负载和负载变化，输出层为期望的气压。通过高效的参数辨识方法训练ANN神经网络，能够使辨识出的神经网络模型很好地模拟气动人工肌肉的静动态特性。Xing等[102]采用回声状态网络(Echo State Network,ESN)对气动人工肌肉进行建模，利用最小二乘法在线辨识模型中的参数，并结合反馈PID控制对气动人工肌肉的轨迹跟踪控制进行了仿真和实验

研究，结果表明所提出的控制方法比传统的PID控制具有更好的鲁棒性和控制性能；Ahn等[103]采用自适应递归神经网络(Adaptive Recurrent Neural Networks,ARNN)对典型的拮抗式气动肌肉关节轨迹跟踪控制进行了仿真和实验研究，取得了良好的控制效果。

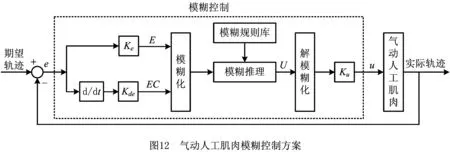
模糊逻辑控制应用模糊集合理论统筹考虑系统的一种控制方式[104]。因为模糊控制不依赖于被控对象的数学模型，只需要现场操作人员和有关专家的经验、知识或操作数据，所有非线性均被考虑到模糊规则中，所以在非线性、大干扰、无明确数学模型的调节上具有优势，可实现对复杂对象的有效控制。图12所示为气动人工肌肉的基本模糊控制方案[105]，它包括模糊化、模糊规则、模糊推理和解模糊4部分。模糊PID控制器因为不依赖于对象模型，其用语言变量描述系统特征，不需要被控制对象精确的数学模型，并能够依据系统的动态信息和模糊控制规则进行推理来获得合适的控制量，所以具有较强的鲁棒性并能实现PID 控制器的参数在线自调整，改善了PID 控制器的性能，可以适应控制系统的参数变化和工作条件变化。为了对一种由气动人工肌肉驱动的踝关节康复机器人进行轨迹跟踪控制，Xie等[106]采用模糊前馈控制器描述气动人工肌肉的迟滞等非线性现象，并采用修正遗传算法辨识优化模糊控制器中的参数，该方法具有良好的轨迹跟踪效果；Tóthová等[107]采用混合模糊自适应控制方法对气动人工肌肉轨迹跟踪控制进行了仿真研究，验证了控制方法的有效性；Nuchkrua等[108]采用模糊自调节PID控制的方法对一种混合驱动的气动人工肌肉进行了控制仿真研究，并在文献[109]中进行了进一步实验验证，与PID控制相比，该方法显著改善了超调量和响应时间等控制性能，提高了控制系统的鲁棒性和稳定性。

5 问题与展望

纵览MicKibben型气动人工肌肉的相关研究文献可见，国内外对气动人工肌肉的特性进行了系统性研究，取得了较大进展，但由于气动人工肌肉及其控制技术是机械、气动、控制、材料等技术的集中体现，要更好地将其应用于实际中还有诸多问题，笔者认为应该在以下方面做进一步研究。

5.1 气动人工肌肉结构改进

气动人工肌肉由橡胶管和包裹在其外面的编织网组成，因此具有结构简单、重量轻、柔性大的优点。然而，橡胶管的低模量、大形变、高回弹等性质导致其存在收缩率低、力量小及寿命短的缺陷，从而限制了其进一步应用与推广[110-111]。为了解决上述问题，一些学者对气动人工肌肉的结构进行了改进，通过使用强化玻璃纤维使气动人工肌肉具有更大的收缩率与拉力，并且寿命更长，特别是这种气动人工肌肉在等压和等长实验中与人类肌肉更类似[112]。同时，为了解决气动肌肉输出力非线性、外接多种传感器导致的机构笨重与结构复杂化，一些学者尝试将阀和传感器嵌入气动人工肌肉中来提高其力学和控制性能，取得了良好的效果[113-114]。

5.2 气动人工肌肉迟滞建模

气动人工肌肉迟滞特性的变化是连续、非重复的，且取决于负载，控制难度体现在多映射性和记忆性。这些特性使常用的经典控制理论和现代控制理论都难以对气动人工肌肉实施有效控制。此外，气动人工肌肉的迟滞是非对称性的多环，但现有研究多采用对称型的迟滞模型描述其迟滞环，因而无法真实反映其迟滞特性。需要指出的是，有学者尝试采用神经网络的方法辨识气动人工肌肉的迟滞特性[115-116]，但从理论上来说，神经网络只能逼近连续的一一映射或多对一映射，不能辨识迟滞非线性这类具有记忆性的多映射非线性现象[117]，因此简单的ANN并不适用于辨识气动人工肌肉的迟滞非线性。有学者在压电陶瓷等领域采用转换算子[118]与扩张空间[119]等方法来尝试解决这一问题，已取得了较好的效果，但在气动人工肌肉中尚未见到相关的应用实例。近两年来，一些学者尝试将压电陶瓷、作动器、形状记忆合金中迟滞特性的最新理论研究成果应用于气动人工肌肉，并取得了较好的成果[120-122]。此外，寻找结构简单的迟滞特性模型和简便的参数辨识算法，以尽量简化控制系统的复杂程度也是一种可供选择的思路。为此，本文提出一种效果良好的修正的广义PI(Modified Generalized Prandtl-Ishlinskii, MGPI)模型，该模型兼具修正的PI (Modified Prandtl-Ishlinskii，MPI)模型能描述非对称型迟滞和广义PI(Generalized Prandtl-Ishlinskii，GPI)模型参数少的优点，且比两者所需算子的个数更少、辨识效果更好。

5.3 气动人工肌肉控制策略

基于迟滞补偿的控制策略分为基于力位移迟滞补偿和基于气压位移迟滞补偿的控制。近年来，气压位移迟滞实验因较力位移迟滞实验更为简便而逐渐受到学者们的青睐。需要指出的是，气压位移迟滞与负载相关，因此基于气压位移迟滞补偿的控制策略需要解决的是气动人工肌肉轨迹跟踪控制对负载变化的鲁棒性，目前该问题尚未得到有效解决。气动人工肌肉迟滞特性的变化是连续、非重复的，且取决于负载，其控制难度体现在多映射性和记忆性，这些特性使常用的经典控制理论和现代控制理论都难以对气动人工肌肉实施有效控制。对于智能控制策略而言，早期研究一般通过辨识或简化得到系统线性模型，然后采用极点配置和反馈线性化等线性控制策略，控制误差较大[18]。而传统的神经网络无法辨识迟滞非线性这类具有记忆性的多映射非线性现象，模糊控制对信息简单的模糊处理会导致系统的控制精度降低、动态品质变差。一个较好的研究方向是借鉴各控制算法的优点，综合利用多种控制方法，采用组合控制策略来提高气动人工肌肉的控制精度，例如采用自适应滑模控制来抑制滑模控制的抖振从而更加精确地实现摩擦补偿[123]；利用自适应参数在线辨识的方法辨识迟滞模型中的参数，使控制系统对负载变化具有更高的鲁棒性等[124]。

近年来，随着气动人工肌肉应用领域的不断拓展及机器人操作任务复杂程度的不断提高，执行器对柔性和精确定位功能的需求越来越迫切。对气动人工肌肉控制的研究也逐渐从单根气动人工肌肉的控制过渡到基于气动人工肌肉驱动的机器人控制[125]。气动人工肌肉因其柔顺性而具有变刚度特性，尤其适用于主动柔顺控制，因此对气动人工肌肉控制的研究也从单纯的位置控制扩展到主动柔顺控制[126]。但如何在实现气动人工肌肉力控制的同时保证其位置控制的精度，是需要重点研究的方向[127]。

参考文献:

[1] TSAGARAKIS N G, CALDWELL D G. Development and control of a ‘soft-actuated’ exoskeleton for use in physiotherapy and training[J]. Autonomous Robots,2003,15(1):21-33.

[2] BERGEMANN D,LORENZ B,THALLEMER A.Actuating means:USA,6349746[P]. 2002-02-26.

[3] MINH T V, TJAHJOWIDODO T, RAMON H, et al. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model[J]. IEEE/ASME Transactions on Mechatronics,2011,16(1):177-186.

[4] OBIAJULU S C, ROCHE E T, PIGULA F A, et al. Soft pneumatic artificial muscles with low threshold pressures for a cardiac compression device[C]// Proceedings of ASME 2013 International Design Engineering Technical Conferences and Computers & Information in Engineering Conference.New York,N.Y.,USA:ASME,,2013,3(1)：1-8.

[5] MINH T V, KAMERS B, RAMON H, et al. Modeling and control of a pneumatic artificial muscle manipulator joint-part I:modeling of a pneumatic artificial muscle manipulator joint with accounting for creep effect[J]. Mechatronics,2012,22(7):923-933.

[6] LILLY J H, YANG L. Sliding mode tracking for pneumatic muscle actuators in opposing pair configuration[J].IEEE Transactions on Control Systems Technology,2005,13(4):550-558.

[7] HESSELROTH T, SARKAR K, VAN DER SMAGT P P, et al. Neural network control of a pneumatic robot arm[J]. IEEE Transactions on Systems, Man and Cybernetics,1994,24(1):28-38.

[8] VAN DER SMAGT P, GROEN F, SCHULTEN K. Analysis and control of a rubbertuator arm[J]. Biological Cybernetics,1996,75(5):433-440.

[9] DAERDEN F. Conception and realization of pleated pneumatic artificial muscles and their use as compliant actuation elements[D]. Brussels,Belgium:Vrije Universiteit Brussel,1999.

[10] DAERDEN F, LEFEBER D. Pneumatic artificial muscles:actuators for robotics and automation[J]. European Journal of Mechanical and Environmental Engineering,2002,47(1):11-21.

[11] CALDWELL D G, MEDRANO-CERDA G A, GOODWIN M J. Braided pneumatic actuator control of a multi-jointed manipulator[C]//Proceedings of International Conference on Systems,Man and Cybernetics.Washington,D.C.,USA:IEEE,1993:423-428.

[12] HENKE R W. Introduction to fluid power circuits and systems[M]. Boston,Mass.,USA:Addison-Wesley,1970.

[13] MINH T V, TJAHJOWIDODO T, RAMON H, et al. Control of a pneumatic artificial muscle(PAM)with model-based hysteresis compensation[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Washington,D.C.,USA:IEEE,2009:1082-1087.

[14] CALDWELL D G A, MEDRANO-CERDA G A, GOODWIN M. Control of pneumatic muscle actuators[J]. IEEE Control Systems,1995,15(1):40-48.

[15] GORDON K E, SAWICKI G S, FERRIS D P. Mechanical performance of artificial pneumatic muscles to power an ankle-foot orthosis[J]. Journal of Biomechanics,2006,39(10):1832-1841.

[16] TONDU B. Modelling of the McKibben artificial muscle:a review[J]. Journal of Intelligent Material Systems and Structures,2012,23(3):225-253.

[17] KELASIDI E, ANDRIKOPOULOS G, NIKOLAKOPOULOS G, et al. A survey on pneumatic muscle actuators modeling[C]//Proceedings of 2011 IEEE International Symposium on Industrial Electronics.Washington,D.C.,USA:IEEE,2011:1263-1269.

[18] TAO Guoliang, XIE Jianwei, ZHOU hong. Research achievements and development trends of pneumatic artificial muscles[J]. Journal of Mechanical Engineering,2009,45(10):75-83(in Chinese).[陶国良,谢建蔚,周 洪.气动人工肌肉的发展趋势与研究现状[J].机械工程学报,2009,45(10):75-83.]

[19] ZHU Xiaocong. Research on the high precision posture control of parallel manipulator driven by pneumatic muscles[D]. Hangzhou:Zhejiang University,2007(in Chinese).[朱笑丛.气动肌肉并联关节高精度位姿控制研究杭州[D].杭州：浙江大学,2007.]

[20] CHOU C P, HANNAFORD B. Static and dynamic characteristics of McKibben pneumatic artificial muscles[C]//Proceedings of 1994 IEEE International Conference on Robotics and Automation.Washington,D.C.,USA:IEEE,1994: 281-286.

[21] HOCKING E G. Analysis of nonlinear behavior in novel pneumatic artificial muscles[D].Washington,D.C.,USA:University of Maryland, 2012.

[22] TONDU B, LOPEZ P. Theory of an artificial pneumatic muscle and application to the modeling of McKibben artificial muscle[J]. Comptes Rendus-Academie des Sciences,Serie II,1995,320(3):105-114.

[23] TSAGARAKIS N, CALDWELL D G. Improved modelling and assessment of pneumatic muscle actuators[C]//Proceedings of IEEE International Conference on Robotics and Automation.Washington,D.C.,USA:IEEE,2000,4:3641-3646.

[24] GAYLORD R H. Fluid actuated motor system and stroking device:U.S. Patent 2,844,126[P].1958-07-22.

[25] SCHULTE H F. The application of external power in prosthetics and orthotics[M].Washington,D.C.,USA:National Academy of Sciences,1961:94-115.

[26] CHOU C P, HANNAFORD B. Measurement and modeling of McKibben pneumatic artificial muscles[J].IEEE Transactions on Robotics and Automation,1996,12(1):90-102.

[27] TONDU B, LOPEZ P. Modeling and control of McKibben artificial muscle robot actuators[J]. IEEE Control Systems,2000,20(2):15-38.

[28] TONDU B, IPPOLITO S, GUIOCHET J, et al. A seven-degrees-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots[J]. The International Journal of Robotics Research,2005,24(4):257-274.

[29] DOUMIT M, FAHIM A, MUNRO M. Analytical modeling and experimental validation of the braided pneumatic muscle[J]. IEEE Transactions on Robotics,2009,25(6):1282-1291.

[30] FERRARESI C,FRANCO W,BERTETTO A M .Flexible pneumatic actuators:a comparison between the McKibben and the straight fibres muscles[J]. Journal of Robotics and Mechatronics,2001,13(1):56-63.

[31] KOTHERA C S, JANGID M, SIROHI J, et al. Experimental characterization and static modeling of McKibben actuators[J]. Journal of Mechanical Design,2009,131(9):091010.

[32] DAVIS S, TSAGARAKIS N G, CANDERLE J, et al. Enhanced modelling and performance in braided pneumatic muscle actuators[J]. International Journal of Robotics Research,2003,22(3/4):213-228.

[33] DAVIS S, CALDWELL D G. Braid effects on contractile range and friction modeling in pneumatic muscle actuators[J]. The International Journal of Robotics Research,2006,25(4):359-369.

[34] SERRES J L. Dynamic characterization of a pneumatic muscle actuator and its application to a resistive training device[D]. Dayton,Ohio,USA:Wright State University,2008.

[35] HILL A V.The heat of shortening and the dynamic constants of muscle[J].Proceedings of the Royal Society of London. Series B,Biological Sciences,1938,126(843):136-195.

[36] KLUTE G K, CZERNIECKI J M, HANNAFORD B. Artificial muscles:actuators for biorobotic systems[J]. The International Journal of Robotics Research,2002,21(4):295-309.

[37] COLBRUNN R W, NELSON G M, QUINN R D. Modeling of braided pneumatic actuators for robotic control[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington,D.C.,USA:IEEE,2001,4:1964-1970.

[38] COLBRUNN R W. Design and control of a robotic leg with braided pneumatic actuators[D]. Cleveland,Ohio,USA:Case Western Reserve University,2000.

[39] REYNOLDS D B, REPPERGER D W, PHILLIPS C A, et al. Modeling the dynamic characteristics of pneumatic muscle[J]. Annals of Biomedical Engineering,2003,31(3):310-317.

[40] SERRES J L, REYNOLDS D B, PHILLIPS C A, et al. Characterisation of a phenomenological model for commercial pneumatic muscle actuators[J]. Computer Methods in Biomechanics and Biomedical Engineering,2009,12(4):423-430.

[41] REPPERGER D W, JOHNSON K R, PHILLIPS C A. A VSC position tracking system involving a large scale pneumatic muscle actuator[C]//Proceedings of the 37th IEEE Conference on Decision and Control.Washington,D.C.,USA:IEEE,1998,4:4302-4307.

[42] REPPERGER D W, JOHNSON K R, PHILIPS C A. Nonlinear feedback controller design of a pneumatic muscle actuator system[C]//Proceedings of the 1999 American Control Conference.Washington,D.C.,USA:IEEE,1999,3:1525-1529.

[43] ZHANG Zengmeng, GONG Yongjun, SUN Zhengwen, et al. Pressure control and static characteristic experiments of water hydraulic artificial muscle[J]. Transactions of Beijing Institute of Technology,2015,35(9):892-897(in Chinese).[张增猛,弓永军,孙正文,等.水压人工肌肉的压力控制与静态特性试验[J].北京理工大学学报,2015,35(9):892-897.]

[44] WICKRAMATUNGE K C, LEEPHAKPREEDA T. Empirical modeling of pneumatic artificial muscle[C]//Proceedings of the International Multiconference of Engineers and Computer Scientists.New York,N.Y., USA:AIP Publishing,2009.

[45] WICKRAMATUNGE K C, LEEPHAKPREEDA T. Study on mechanical behaviors of pneumatic artificial muscle[J]. International Journal of Engineering Science,2010,48(2):188-198.

[46] XIE Shenglong, LIU Haitao, MEI Jiangping, et al. Modeling and compensation of asymmetric hysteresis for pneumatic artificial muscles with a modified generalized Prandtl-Ishlinskii model[J]. Mechatronics, 2018, 52: 49-57.

[47] PUJANA-ARRESE A, MENDIZABAL A, ARENAS J, et al. Modelling in Modelica and position control of a 1-DoF set-up powered by pneumatic muscles[J]. Mechatronics,2010,20(5):535-552.

[48] XIE Shenglong, LIU Haitao, MEI Jiangping, et al. Simulation of tracking control of pneumatic artificial muscle based on fast switching valves[J]. Transactions of the Chinese Society of Agricultural Machinery,2017,48(1):368-374(in Chinese).[谢胜龙,刘海涛,梅江平,等.基于高速开关阀的气动人工肌肉轨迹跟踪控制仿真[J].农业机械学报,2017,48(1):368-374.]

[49] BERTETTO A M, RUGGIU M. Characterization and modeling of air muscles[J]. Mechanics Research Communications,2004,31(2):185-194.

[50] SHAN Y, PHILEN M P, BAKIS C E, et al. Nonlinear-elastic finite axisymmetric deformation of flexible matrix composite membranes under internal pressure and axial force[J]. Composites Science and Technology,2006,66(15):3053-3063.

[51] ZANG Kejiang. Mechanism and design theory research of braided type pneumatic artificial muscle[D]. Harbin:Northeaset Forestry University,2012(in Chinese).[臧克江.编织型气动人工肌肉工作机理及设计理论研究[D].哈尔滨：东北林业大学,2012.]

[52] NOZAKI T, NORITSUGU T. Motion analysis of mckibben type of pneumatic rubber artificial muscle with finite element method(model without friction between plastics fibers)[J]. The Japan Society of Mechanical Engineers，2009，754(75):1755-1762.

[53] NOZAKI T, NORITSUGU T. Motion analysis of McKibben type pneumatic rubber artificial muscle with finite element method[J].International Journal of Automation Technology,2014,8(2):147-158.

[54] YANG Gang, LI Baoren, FU Xiaoyun. Research on dynamic characteristics of a pneumatic muscle actuator[J]. China Mechanical Engineering,2006,17(12):1294-1298(in Chinese).[杨 钢,李宝仁,傅晓云.气动人工肌肉系统动态特性研究[J].中国机械工程,2006,17(12):1294-1298.]

[55] LI Baoren, LIU Jun, YANG Gang. Modeling and simulation of pneumatic muscle system[J]. Journal of Mechanical Engineering,2003,39(7):23-28(in Chinese).[李宝仁，刘 军，杨 钢.气动人工肌肉系统建模与仿真[J].机械工程学报,2003,39(7):23-28.]

[56] YANG Gang, LI Baoren, LIU Jun. A new analytical method on characteristics of artificial pneumatic muscle actuator[J]. Chinese Hydraulics & Pneumatics,2002(10):22-25(in Chinese).[杨 钢,李宝仁,刘 军.气动人工肌肉特性分析的新方法[J].液压与气动,2002(10):22-25.]

[57] YANG Gang. Research on pneumatic muscle actuator position servo system and its application[D]. Wuhan:Huazhong University of Science and Technology,2004(in Chinese).[杨 钢.气动人工肌肉位置伺服系统研究及其应用[D]武汉：华中科技大学,2004.]

[58] HILDEBRANDT A, SAWODNY O, NEUMANN R, et al. A flatness based design for tracking control of pneumatic muscle actuators[C]//Proceedings of the 7th International Conference on Control, Automation,Robotics and Vision. Washington,D.C.,USA: IEEE,2002,3:1156-1161.

[59] MINH T V, TJAHJOWIDODO T, RAMON H, et al. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation[J]. Mechatronics,2010,20(3):402-414.

[60] HILDEBRANDT A, SAWODNY O, NEUMANN R, et al. Cascaded control concept of a robot with two degrees of freedom driven by four artificial pneumatic muscle actuators[C]//Proceedings of American Control Conference. Washington, D.C.,USA:IEEE,2005:680-685.

[61] MAYERGOYZ I D. Mathematical models of hysteresis and their applications[M]. Cambridge,Mass.,USA:Academic Press,2003.

[62] INOUE K. Rubbertuators and applications for robots[C]//Proceedings of the 4th International Symposium on Robotics Research. Cambridge,Mass.,USA:MIT Press,1988:57-63.

[63] LIN C J, LIN C R, YU S K, et al. Hysteresis modeling and tracking control for a dual pneumatic artificial muscle system using Prandtl-Ishlinskii model[J]. Mechatronics,2015,28:35-45.

[64] MINH T V, TJAHJOWIDODO T, RAMON H, et al. Non-local memory hysteresis in a pneumatic artificial muscle(PAM)[C]//Proceedings of the 17th Mediterranean Conference on Control and Automation. Washington,D.C.,USA:IEEE,2009:640-645.

[65] YUAN Daning, LIU Lilan, LIU Hongzhao, et al. Progress of Pre-sliding friction model[J]. Journal of System Simulation,2009,21(4):1142-1147(in Chinese).[原大宁,刘丽兰,刘宏昭,等.滑动摩擦模型研究现状[J].系统仿真学报,2009,21(4):1142-1147.]

[66] VAN DAMME M,BEYL P,VANDERBORGHT B,et al. Modeling hysteresis in pleated pneumatic artificial muscles[C]// Proceedings of 2008 IEEE Conference on Robotics,Automation and Mechatronics. Washington,D.C.,USA:IEEE,2008:471-476.

[67] HASSANI V, TJAHJOWIDODO T, DO T N. A survey on hysteresis modeling, identification and control[J]. Mechanical Systems and Signal Processing,2014,49(1):209-233.

[68] KOSAKI T, SANO M. Control of a parallel manipulator driven by pneumatic muscle actuators based on a hysteresis model[J]. Journal of Environment and Engineering,2011,6(2):316-327.

[69] SCHREIBER F, SKLYARENKO Y, SCHLÜTER K, et al. Tracking control with hysteresis compensation for manipulator segments driven by pneumatic artificial muscles[C]//Proceedings of 2011 IEEE International Conference on Robotics and Biomimetics.Washington,D.C.,USA:IEEE,2011:2750-2755.

[70] MINH T V, KAMERS B, TJAHJOWIDODO T, et al. Modeling torque-angle hysteresis in a pneumatic muscle manipulator[C]//Proceedings of 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Washington,D.C.,USA:IEEE,2010,58(1):1122-1127.

[71] ZHAO Jie, ZHONG Jun, FAN Jizhuang. Position control of a pneumatic muscle actuator using RBF neural network tuned PID Controller[J]. Mathematical Problems in Engineering,2015(5):1-16.

[72] JIN Guanlin. System Identification of a pneumatic artificial muscle using an embedded system[D]. Taiwan:National Taiwan Normal University.2013(in Chinese).[金冠霖.以嵌入式系統實現人工肌肉氣壓缸之系統識別[D].台湾：国立台湾师范大学,2013.]

[73] ASCHEMANN H, SCHINDELE D. Comparison of model-based approaches to the compensation of hysteresis in the force characteristic of pneumatic muscles[J].IEEE Transactions on Industrial Electronics,2014,61(7):3620-3629.

[74] YANG Hui, HAO Lina, CHEN Yang, et al. Kalman-PID control for chattering phenomena of bionic elbow joint actuated by pneumatic artificial muscles[J]. Control Theory & Applications,2017,34(4):477-482(in Chinese).[杨 辉,郝丽娜,陈 洋,等.针对气动肌肉仿生肘关节抖振现象的Kalman-PID控制[J].控制理论与应用,2017,34(4):477-482.]

[75] KIMURA T, HARA S, FUJITA T, et al. Feedback linearization for pneumatic actuator systems with static friction[J]. Control Engineering Practice,1997,5(10):1385-1394.

[76] HILDEBRANDT A,SAWODNY O,NEUMANN R,et al.A cascaded tracking control concept for pneumatic muscle actuators[C]// Proceedings of European Control Conference.Washington,D.C.,USA:IEEE,2003.

[77] XIE Shenglong, MEI Jiangping, LIU Haitao. Hysteresis modeling and trajectory tracking control of the pneumatic muscle actuator using modified Prandtl-Ishlinskii model[J]. Mechanism and Machine Theory,2018,120:213-224.

[78] BONA B, INDRI M. Friction compensation in robotics:an overview[C]//Proceedings of the 44th IEEE Conference on Decision and Control & European Control Conference. Washington, D.C., USA: IEEE, 2005 :4360-4367.

[79] NA Jing, YANG Guangyu, GAO Guanbin, et al.Parameter estimation error based robust adaptive law design and experiments[J]. Control Theory & Applications,2016,33(7):956-964(in Chiense).[那 靖,杨光宇,高贯斌,等.基于参数估计误差的鲁棒自适应律设计及验证[J].控制理论与应用,2016,33(7):956-964.]

[80] AHN K K, ANH H P H. System identification and self-tuning pole placement control of the two-axes pneumatic artificial muscle manipulator optimized by genetic algorithm[C]//Proceedings of International Conference on Mechatronics and Automation. Washington,D.C.,USA:IEEE,2007:2604-2609.

[81] SLOTINE J E.Applied nonlinear control[M]. Beijing:China Machine Press,2006(in Chinese).[斯洛坦.应用非线性控制[M].北京：机械工业出版社,2006.]

[82] KIMURA T, HARA S, FUJITA T, et al. Control for pneumatic actuator systems using feedback linearization with disturbance rejection[C]//Proceedings of American Control Conference. Washington, D.C., USA:IEEE,1995,1:825-829.

[83] KIMURA T, FUJITA T, HARA S, et al. Control for systems with pneumatic actuator using feedback linearization[J]. Transactions of the Institute of Systems, Control and Information Engineers,1995,8:52-60.

[84] KNESTEL M, HOFER E P, BARILLAS S K, et al. The artificial muscle as an innovative actuator in rehabilitation robotics[J]. IFAC Proceedings Volumes,2008,41(2):773-778.

[85] ALINIA S, HEMMATIAN M, XIE W F, et al. Posture control of 3-DOF parallel manipulator using feedback linearization and model reference adaptive control[C]//Proceedings of the 28th Canadian Conference on Electrical and Computer Engineering.Washington,D.C.,USA:IEEE, 2015:1145-1150.

[86] HU Yueming. Variable structure control theory and applications[M]. Beijing:Science Press,2003(in Chinese).[胡跃明.变结构控制理论与应用[M].北京：科学出版社,2003.]

[87] ASCHEMANN H, SCHINDELE D. Sliding-mode control of a high-speed linear axis driven by pneumatic muscle actuators[J]. IEEE Transactions on Industrial Electronics,2008,55(11):3855-3864.

[88] JOUPPILA V T, GADSDEN S A, BONE G M, et al. Sliding mode control of a pneumatic muscle actuator system with a PWM strategy[J]. International Journal of Fluid Power,2014,15(1):19-31.

[89] JOUPPILA V T, GADSDEN S A, ELLMAN A. Experimental comparisons of sliding mode controlled pneumatic muscle and cylinder actuators[J]. Journal of Dynamic Systems, Measurement and Control,2014,136(4):044503.

[90] SHEN X. Nonlinear model-based control of pneumatic artificial muscle servo systems[J]. Control Engineering Practice,2010,18(3):311-317.

[91] RAHMAN R A,SEPEHRI N. Design and experimental evaluation of a dynamical adaptive backstepping-sliding mode control scheme for positioning of an antagonistically paired pneumatic artificial muscles driven actuating system[J]. International Journal of Control,2017,90(2):249-274.

[92] WANG Binrui, SHEN Guoyang, JIN Yinglian, et al. Sliding Mode Control of Cascade Pneumatic Muscles of Elbow Joint Based on Disturbance Observer[J]. Acta Armamentarii,2017,38(4):793-801(in Chinese).[王斌锐,沈国阳,金英连,等.基于干扰观测器的级联气动肌肉肘关节滑模控制[J].兵工学报,2017,38(4):793-801.]

[93] TANG Wei, SHI Songjiao, WANG Mengxiao, et al. Three important methods in robust control theory: a brief review (I) [J]. Journal of Shaanxi University of Science, 2000, 19(4): 49-53 (in Chinese).[汤 伟, 施颂椒, 王孟效, 等. 鲁棒控制理论中3种主要方法综述(一)[J]. 陕西科技大学学报, 2000, 19(4): 49-53.]

[94] LIU Xingtang. Applied adaptive control[M]. Xi’an:Northwestern Polytechnical University Press,2003(in Chinese).[刘兴堂.应用自适应控制[M].西安：西北工业大学出版社,2003.]

[95] LIN L H, YEN J Y, WANG F C. Robust control for a pneumatic muscle actuator system[J]. Transactions of the Canadian Society for Mechanical Engineering,2013,37(3):581-590.

[96] AMATO F, COLACINO D, COSENTINO C, et al. Robust and optimal tracking control for manipulator arm driven by pneumatic muscle actuators[C]//Proceedings of 2013 IEEE International Conference on Mechatronics.Washington,D.C.,USA:IEEE,2013:827-834.

[97] WANG Yang, ZHANG Qiang, XIAO Xiaohui. Trajectory tracking control of the bionic joint actuated by pneumatic artificial muscle based on robust modeling[J]. Robot,2016,38(2):248-256(in Chinese).[王 杨,张 强,肖晓晖.基于鲁棒建模的气动人工肌肉驱动仿生关节的轨迹跟踪控制[J].机器人,2016,38(2):248-256.]

[98] XIN Bin, CHEN Jie, PENG Zhihong. Intelligent optimized control:overview and prospect[J]. Acta Automatica Sinica,2013,39(11):1831-1848(in Chinese).[辛 斌,陈 杰,彭志红.智能优化控制：概述与展望[J].自动化学报,2013,39(11):1831-1848.]

[99] CAI Zixing. Advance in research of intelligent control and mobile robots[J]. Journal of Central South University of Technology:Natural Science,2005,36(5):721-726(in Chinese).[蔡自兴.智能控制及移动机器人研究进展[J].中南大学学报：自然科学版,2005,36(5):721-726.]

[100] LI Shaoyuan, CHEN Zengqiang.The new progresses in intelligent control(II)[J]. Control and Decision,2000,15(2):136-140(in Chinese).[李少远,陈增强.智能控制的新进展(II)[J].控制与决策,2000,15(2):136-140.]

[101] SONG Chunsheng,XIE Shengquan,ZHOU Zude, et al. Modeling of pneumatic artificial muscle using a hybrid artificial neural network approach[J]. Mechatronics,2015,31:124-131.

[102] XING K, WANG Y, ZHU Q, et al. Modeling and control of McKibben artificial muscle enhanced with echo state networks[J]. Control Engineering Practice,2012,20(5):477-488.

[103] AHN K K, ANH H P H. Design and implementation of an adaptive recurrent neural networks(ARNN)controller of the pneumatic artificial muscle(PAM)manipulator[J]. Mechatronics,2009,19(6):816-828.

[104] LI Shaoyuan, CHEN Zengqiang.The new progresses in intelligent control(I)[J]. Control and Decision,2000,15(1):1-5(in Chinese).[李少远,陈增强.智能控制的新进展(Ⅰ)[J].控制与决策,2000,15(1):1-5.]

[105] CHANG M K, LIOU J J, CHEN M L. T-S fuzzy model-based tracking control of a one-dimensional manipulator actuated by pneumatic artificial muscles[J]. Control Engineering Practice,2011,19(12):1442-1449.

[106] XIE S Q, JAMWAL P K. An iterative fuzzy controller for pneumatic muscle driven rehabilitation robot[J]. Expert Systems with Applications,2011,38(7):8128-8137.

[108] NUCHKRUA T, LEEPHAKPREEDA T. Fuzzy self-tuning PID control of hydrogen-driven pneumatic artificial muscle actuator[J]. Journal of Bionic Engineering,2013,10(3):329-340.

[109] NUCHKRUA T, LEEPHAKPREEDA T, CHEN S L. Experimental validation for fuzzy control of servo pneumatic artificial muscle driven by metal hydride[J]. International Journal of Fuzzy Systems,2016,18(6):956-970.

[110] TONDU B, IPPOLITO S, GUIOCHET J, et al. A seven-degrees-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots[J]. The International Journal of Robotics Research,2005,24(4):257-274.

[111] SHIN D, YEH X, KHATIB O. A new hybrid actuation scheme with artificial pneumatic muscles and a magnetic particle brake for safe human-robot collaboration[J]. The International Journal of Robotics Research,2014,33(4):507-518.

[112] NAKAMURA T, SAGA N, YAEGASHI K. Development of a pneumatic artificial muscle based on biomechanical characteristics[C]//Proceedings of 2003 IEEE International Conference on Industrial Technology.Washington,D.C.,USA:IEEE,2003,2:729-734.

[113] PARK Y L, WOOD R J. Smart pneumatic artificial muscle actuator with embedded microfluidic sensing[C]//Proceedings of 2013 IEEE Conference on Sensors.Washington,D.C.,USA:IEEE,2013:1-4.DOI:0.1109/ICSENS.2013.6688298.

[114] PARK Y L, SANTOS J, GALLOWAY K G, et al. A soft wearable robotic device for active knee motions using flat pneumatic artificial muscles[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Washington,D.C.,USA:IEEE,2014:4805-4810.

[115] CUI Xia, SHI Guanglin, SHEN Wei. Study on hystetresis of pneumatic artificial muscle based on group method of tata handing neural network[J]. Journal of Shanghai Jiaotong University，2012，46(6):931-935(in Chinese).[崔 霞，施光林，沈 伟.基于分组数据处理神经网络气动人工肌肉迟滞特性[J].上海交通大学学报，2012，46(6):931-935.]

[116] BAO Chunlei, WANG Binrui, JIN Yinglian,et al. Model free adaptive CMAC hysteresis compensation control of the pneumatic muscle joint[J]. Robot，2015，37(3):298-303(in Chinese).[鲍春雷，王斌锐，金英连，等.气动肌肉关节的无模型自适应CMAC迟滞补偿控制[J].机器人，2015，37(3):298-303.]

[117] WEI J D, SUN C T. Constructing hysteretic memory in neural networks[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics,2000,30(4):601-609.

[118] ZhAO X, TAN Y. Neural network based identification of preisach-type hysteresis in piezoelectric actuator using hysteretic operator[J]. Sensors and Actuators A:Physical,2006,126(2):306-311.

[119] BERNARD Y, MENDES E, BOUILLAULT F. Dynamic hysteresis modeling based on Preisach model[J].IEEE Transactions on Magnetics,2002,38(2):885-888.

[120] LIU Yixiang,ZANG Xizhe,LIN Zhenkun,et al. Modelling length/pressure hysteresis of a pneumatic artificial muscle using a modified Prandtl-Ishlinskii model[J]. Journal of Mechanical Engineering,2017,63(1):56-64.

[121] ZANG X, LIU Y, HENG S, et al. Position control of a single pneumatic artificial muscle with hysteresis compensation based on modified Prandtl-Ishlinskii model[J]. Bio-Medical Materials and Engineering,2017,28(2):131-140.

[122] MEI Jiangping, XIE Shenglong, LIU Haitao, et al.Hysteresis modeling and compensation of pneumatic artificial muscles using the generalized Prandtl-Ishlinskii model[J].Journal of Mechanical Engineering,2017,63(11):657-665.

[123] TAN Wenbin, LI Xingfei, QIU Zurong, et al. Adaptive sliding friction compensation method based on modified LuGre model[J]. Journal of Tianjin University:Science and Technology,2015,48(5):463-467(in Chinese).[谭文斌,李醒飞,裘祖荣,等.基于改进型LuGre模型的自适应滑模摩擦补偿方法[J].天津大学学报:自然科学与工程技术版,2015,48(5):463-467.]

[124] XIANG Hongbiao, TAN Wenbin, LI Xingfei, et al. Adaptive friction compensation based on LuGre model[J]. Journal of Mechanical Engineering,2012,48(17):70-74(in Chinese).[向红标,谭文斌,李醒飞,等.基于LuGre模型的自适应摩擦补偿[J].机械工程学报,2012,48(17):70-74.]

[125] MENG Wei, LIU Quan, ZHOU Zude, et al. Recent development of mechanisms and control strategies for robot-assisted lower limb rehabilitation[J]. Mechatronics,2015,31:132-145.

[126] JAMWAL P K, HUSSAIN S, GHAYESH M H, et al. Impedance control of an intrinsically compliant parallel ankle rehabilitation robot[J]. IEEE Transactions on Industrial Electronics,2016,63(6):3638-3647.

[127] LIU Yu, WANG Tao, FAN Wei.Mechanism and impedance control of the ball universal joint robot driven by the Pneumatic muscle actuator group[J]. Journal of Mechanical Engineering,2013,49(15):28-33(in Chinese).[刘 昱,王 涛,范 伟.基于气动肌肉群驱动球关节机器人结构及阻抗控制[J].机械工程学报,2013,49(15):28-33.]