基于多传感器测量的孔组位置度快速检测方法

李 兵，兰梦辉+，孙 彬，侯 颖

(1.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安 710049;2.西安工业大学 机电工程学院，陕西 西安 710021)

0 引言

工业机器人是高端智能装备产业的代表，从2013年开始，我国已持续成为世界各国中最大的工业机器人市场。然而在工业机器人产业化进程中，存在很多阻碍发展的难题，其中就包括以关节RV减速器为代表的核心零部件不能自给自足，其80%的国内市场被跨国品牌占据。为提高国内关节RV减速器生产的能力，降低机器人生产成本，必须形成具有自主产权的工业机器人关节减速器生产线，其中主要工作包括研发关节RV减速器各零部件的生产加工工艺以及研发生产线上的快速检测方法[1-3]。本文即是服务于国内正在建设的关节RV减速器生产线，解决摆线轮轴承安装孔位置度的在线快速检测问题，采用多传感器系统，并结合计算机辅助满足生产线上的快速检测要求。

目前基于多传感器的检测方式应用广泛，研究者们开发了多传感器测量系统，集成多个或多类传感器进行组合测量已经成为工业检测的重要发展趋势[4-5]。因为大多数复杂零件都由若干曲面和平面组成，所以测量要素的信息较多。以三坐标测量机(Coordinate Measuring Machine，CMM)为代表的接触式测量方法在工业测量中有着广泛的应用，但是由于其采样时间较长，无法满足复杂曲面零件在线测量的节拍要求；单一位移传感器虽然测量精度高、速度快，却只能测量一维要素，在测量复杂零件时需要大量的传感器配合实现[6-8]。非接触式测量技术中的激光扫描传感器、机器视觉等新型视觉测量产品，理论上可以一次获得多个方向的曲面测量数据，满足多要素测量的要求，但是其测量精度无法满足一些精度要求较高的测量项目，并且对于复杂的零件，其信息处理过程可能耗时较长。Nashman等[9]提出一种视觉—接触相结合的多传感器测量系统，该系统在CMM的基础上集成了触发式测头、相机、激光测头，并以CMM为主要测量工具，采用非接触测量传感器提供反馈信息对CMM坐标位置进行校正，共同完成测量。国内的清华大学[10]、西安交通大学[11-12]、天津大学[13]、浙江大学[14]等高校近年来纷纷对多传感器测量技术与应用进行研究，取得了一定的成果。

本文设计了一种多传感器测量系统，通过多支传感器组合测量的方法采样获得工件的实际要素信息，将实测件与标定件的圆心位置关系进行对比，最终完成位置度误差的判定。在系统误差分析和传感器误差补偿后进行实验，并与权威CMM的测量结果进行对比验证，证明检测结果准确可靠。该方法只需一次对标过程即可实现多次重复测量，具有测量速度快、精度高的优点，能够满足生产线上快速检测的节拍要求。

1 测量系统

1.1 摆线轮孔组位置度介绍

位置度作为位置公差的一种，是被测要素的实际位置偏移理想位置的程度，理想位置相对于基准或几何图框确定。位置度误差直接影响零部件的装配质量，制造或生产出工件之后必须检查其位置度误差，以确保零件质量。

对于本文所研究的RV减速器关键零件——摆线轮，需检测并评价摆线轮上3个圆周分布的轴承安装孔互相之间的位置关系，如图1所示。图中以中心定位孔的圆心为基准，圆周3个轴承安装孔的圆心位置相对于基准模拟出的理想位置所形成的公差带f1，f2，f3即为圆周分布的轴承安装孔的位置度误差，如图2所示。

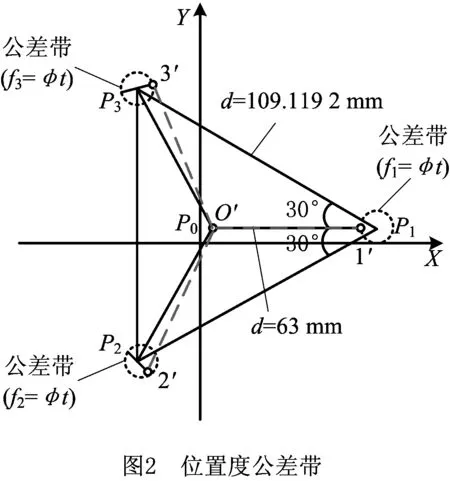
1.2 多传感器测量装置设计

本测量方法要在生产线上使用，并要求实现对摆线轮轴承安装孔位置度的快速测量。传统位置度量规检测方法的测量精度达不到0.001 mm，而三坐标机检测的检测速度和效率不满足生产线上的检测。因此设计一种针对摆线轮圆周分布轴承安装孔位置度的检测装置，通过多支传感器组合测量的方法进行位置度误差检测。根据摆线轮4个孔(包括中心孔和圆周分布3个轴承安装孔)的标准尺寸设计4个导向套，在圆周3个导向套的外围每隔90°的方向上各分布1支电感式位移传感器，中心导向套每隔120°的方向上各分布1支电感式位移传感器，共计15支电感式位移传感器，其中圆周的导向套内各有两个传感器的轴线方向与中心导向套内传感器的轴线方向一致，具体位置如图3所示。位置度测量部由传感器导向套、基板、支架等组成，其中设计的关键是基板上3个圆周导向套及中心导向套上传感器测头的开孔位置，实物如图4所示。测量系统的测头安装误差将在第3章中进行误差分析。

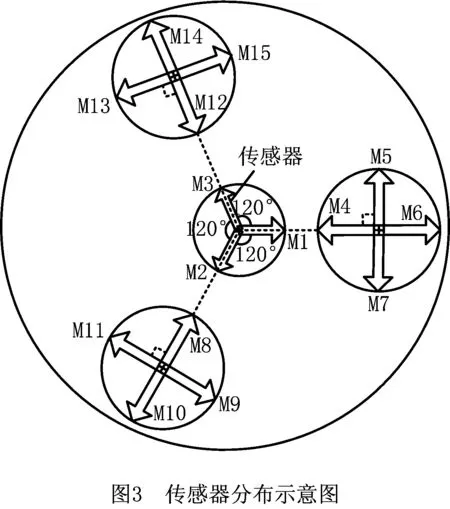
2 测量方案及评定算法

本测量方案需要一个已知圆周均布的3个轴承安装的孔心距和3个孔位置度参数数据的摆线轮标准件(型号：320E)，这里使用LeitzReference15.09.07桥式CMM(测量误差小于2 μm)对标准件进行检测，后期将对该检测结果与本测量方案的实验结果进行对比。

测量过程首先对摆线轮的标准件进行对标过程，测量方案的流程如图5所示。

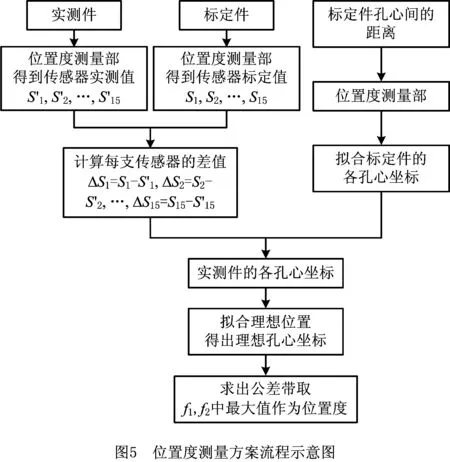
参照测量方案流程，具体步骤如下：

(1)分别在位置度测量部放摆线轮的标定件和实测件，分别获得15支传感器的数据，并计算每支传感器标定值与实测值的差值：

(1)

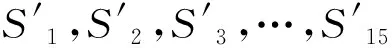
(2)在标定件圆周均布3个孔心之间的距离d|01|,d|02|,d|03|(分别为62.998 9 mm,62.998 2 mm,63.002 7 mm)已知的前提下，将各孔心距在位置度测量部传感器形成的坐标系下进行换算，得到各孔心坐标值(标定件各孔圆心如图6中的标示O，1，2，3)：

(2)

转换后的坐标分别为O(X0，Y0)，1(X1，Y1)，2(X2，Y2)，3(X3，Y3)。

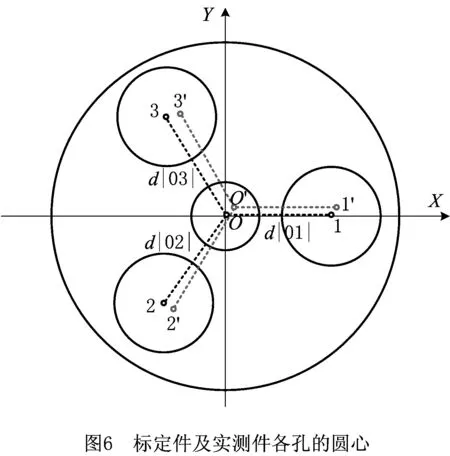
(3)在位置度测量部传感器形成的同一坐标系下，将传感器实测值与标定值之差转化成摆线轮标定件与实测件圆周曲柄轴安装孔各孔心坐标偏差量，并将式(1)带入下式(实测件各孔圆心如图6中标示O′，1′，2′，3′)：

(3)

将式(2)和式(3)代入式(4)，则实测件的圆周曲柄轴安装孔圆心坐标可由标定件圆心坐标与圆心坐标偏差量叠加得到，即：

(4)

转换后的坐标分别为O′(X0′，Y0′)，1′(X1′，Y1′)，2′(X2′，Y2′)，3′(X3′，Y3′)；

(4)在得到实测件各孔圆心坐标之后，将d|1′0|，d|2′0|，d|3′0|中最接近63 mm(标准孔心距)的作为基准参照，例如|d|1′0|-63 mm|最小，参照图2，将O′1′所在直线及O′(P0)作为基准，拟合出圆周均布的3个孔圆心的理想位置P1，P2，P3，通过O′与1′之间的距离为63 mm及O′，1′与P1在一条直线的几何关系，建立如下方程组，先求出

(5)

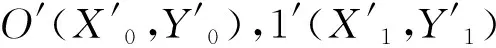
再通过O′(P0),P1,P2,P3之间的特定位置关系建立如下方程组，求出

(6)

(5)在得出P1，P2，P3的坐标后，其与实测件孔心1′，2′，3′形成的公差带即为各孔的位置度，评定公式分别为：

(7)

本测试系统的软件是Windows操作系统下基于对话框的MFC应用程序，应用C语言将算法写入该测试软件中。在实际生产过程中，每次测量前均需对摆线轮标定件进行标定。检测摆线轮实测件时，加上安装工件的时间，整个测量节拍小于10 s，达到了对摆线轮轴承安装孔位置度快速测量的目的，能够满足工业机器人RV减速器生产线上检测的要求。

3 测量系统误差分析及补偿

影响测量系统精度的因素还有系统的机构误差和传感器自身的测量误差。机构误差主要来源于传感器测头位置能否准确按照多传感器测量装置的方案分布，传感器自身的测量误差主要来源于其自身的测量精度。本文对机构误差进行详细分析，并对传感器自身的测量误差进行建模和补偿，以保证系统在生产线现场的测量精度。

另外，由于测量系统旨在实现工业机器人RV减速器生产线上对摆线轮的检测，测量精度会受现场温度、振动等因素的影响，其中现场温度主要影响工件的尺寸变化，振动主要影响传感器的测量值，这些干扰均会影响被测件的位置度误差值。针对现场温度的影响，采用一种方案对测量状况进行调节；针对现场振动因素的影响，采用机械隔振、电路隔离和件滤波等，将振动的影响降至最低。

3.1 机构误差分析

从测量方案及测量装置的设计可知，影响传感器测头处于理想位置的因素(机构误差)有导向套与被测孔间隙所造成的误差，以及测头的安装误差。其中测头的安装误差由位置度测量部中导向套孔的加工偏差和传感器测头在装夹过程中造成的偏差综合影响造成，分为径向倾角误差和轴向倾角误差。

被测件摆线轮有中心孔和圆周分布的轴承安装孔，其标准内径尺寸分别为52.000 mm，55.000 mm，为了使导向套能顺利插入被测孔并尽量减小间隙造成的误差，在测量装置的设计中，将导向套尺寸设计为51.900 mm，54.900 mm，即最大间隙约为0.1 mm(100 μm)。根据第2章的测量方案及评定算法，位置度误差评定所需的初始数据是每支传感器标定值与实测值的差值ΔS1，ΔS2，ΔS3，…，ΔS15，差值必定在0～100 μm之间。

下面对其中一支传感器在中心孔和圆周分布的轴承安装孔的具体情况进行误差分析。

(1) 导向套与被测孔的间隙误差

由于导向套与被测孔之间有一定间隙，在安装被测件时会造成各个方向的不确定偏移。根据导向套与被测孔的设计尺寸，它们之间的最大间隙约为0.1 mm，图7所示为偏移量最大的情况。对于中心孔有(52/2)×sinθ1=0.05，对于圆周孔有(55/2)×sinθ2=0.05，因此最大偏移角度分别为θ1≈0.110°，θ2≈0.104°。由于θ1与θ2的偏差很小，下面将统一以θ=0.110°代替计算。

间隙误差在标定和测量过程造成的标定值S与实测值S′的误差值分别为S×(1-cosθ)、S′×(1-cosθ)，因为位置度的评定算法所需的初始数据是每支传感器标定值与实测值的差值ΔS1，ΔS2，ΔS3，…，ΔS15，所以最终由间隙误差造成的单支传感器数据的误差值为ΔS×(1-cosθ)。因为ΔS在0～100 μm之间，所以误差值在0～1.84×10-4μm之间，可忽略不计。

(2) 径向倾角误差

径向倾角误差由导向套孔的加工偏差，以及传感器测头在装夹过程中造成的偏差组成，根据加工精度的要求和装夹水平可知，测头相对于标准位置左右偏移约为0.1 mm，如图7所示。设径向倾角误差角度为α，对于中心孔有(52/2)×sinα1=0.1，对于圆周孔有(55/2)×sinα2=0.1，因此最大偏移角度分别为α1≈0.220°，α2≈0.208°。由于α1与α2的偏差很小，下面将统一以α=0.22°代替计算。

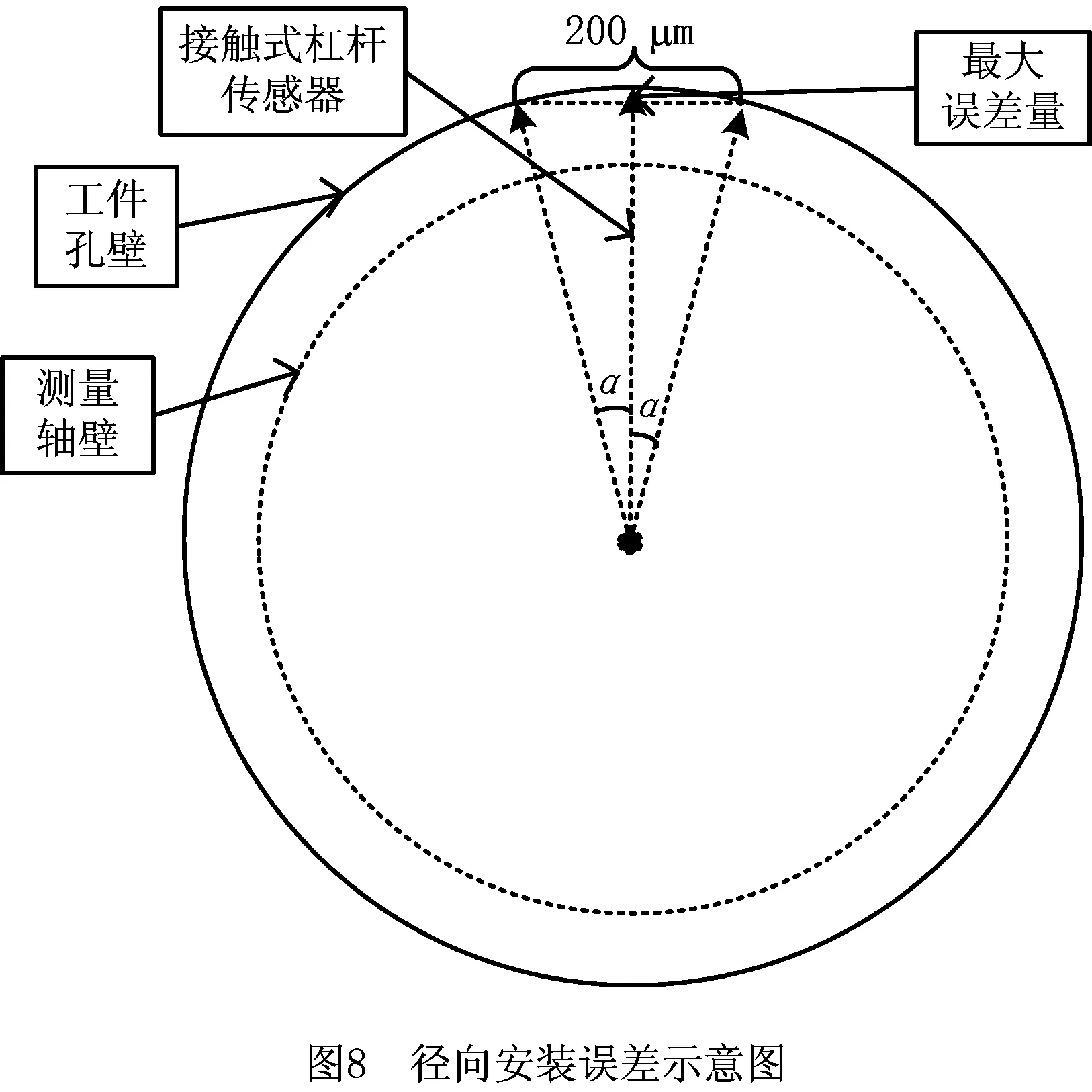
同间隙误差，由径向倾角误差所造成的单支传感器数据的误差值为ΔS×(1-cosα)。因为差值ΔS在0～100 μm之间，所以误差值在0～7.37×10-4μm之间，可忽略不计。

(3)轴向倾角误差

轴向倾角误差产生的原因同径向倾角误差，根据加工精度的要求和装夹水平可知，测头相对于标准位置的上下偏移约为0.1 mm，如图9所示。设径向倾角误差角度约为β，对于中心孔有(52/2)×tanβ1=0.1，对于圆周孔有(55/2)×tanβ2=0.1，因此最大偏移角度分别为β1≈0.220°，β2≈0.208°，由于β1与β2的偏差很小，下面将统一以β=0.22°代替计算。

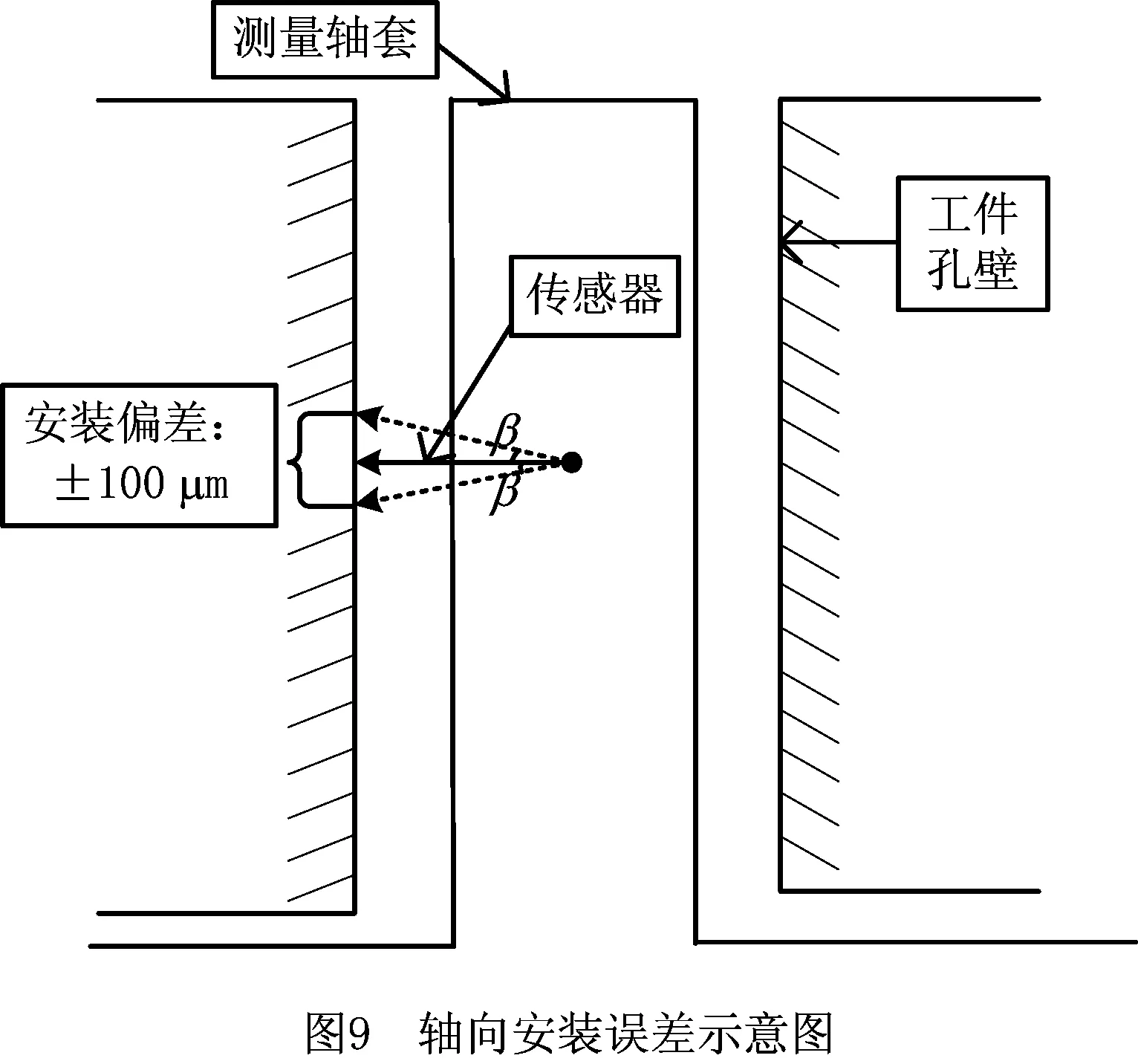
同间隙误差，由径向倾角误差造成的单支传感器数据的误差值为ΔS×(1-cosβ)。因为ΔS在0～100 μm之间，所以误差值在0～7.37×10-4μm之间，可忽略不计。

上面分析了影响机构误差的几个主要因素，求出可能产生的最大误差值均在纳米级，对本测量系统的测量精度(微米级)几乎没有影响，因此机构误差并不是影响测量精度的主要原因。

3.2 生产线上的影响因素分析

考虑到RV减速器生产线的现场温度、振动等因素对测量精度的影响，需采取一定措施进行保护，将现场对测量精度的影响降至最低。

(1) 温度影响

孔型零件的受热变形量取决于零件的材料、几何尺寸、受外力情况以及所处的温度场。本测量方案为静态测量，排除受外力的情况，传统的孔型零件内径的受热变形量计算方法通常是利用一个线性公式D1=D0(1+αΔT)，其中考虑了孔型零件的内径、材料的热膨胀系数和孔型所处温度场的变化量。针对摆线轮的实际外形尺寸，在只考虑圆周分布的3个轴承安装孔热变形的情况下，设其初始内径、外径分别为d0，D0，零件在温度变化前的体积为

(8)

当温度变化后，孔形零件的儿何尺寸发生改变，其内径、外径分别为d1，D1，且D1=D0(1+αΔT)，温度改变后孔的体积为

(9)

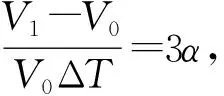
摆线轮的外径尺寸D0=200 mm，3个轴承安装孔内径为55 mm；材质为GCr15，其在20 ℃～100 ℃范围内的热膨胀系数约为1.4×10-5/℃。假设零件均处于稳态均匀的温度场中，计算得：当温度变化量ΔT=5 ℃时，摆线轮的内径尺寸变化量约为2.7 μm；当ΔT=10 ℃时，摆线轮的内径尺寸变化量约为5.4 μm；当ΔT=20 ℃时，摆线轮的内径尺寸变化量约为10.8 μm。内径的变化会使方案中的圆心坐标定位发生偏移，从而造成位置度误差测量偏差，然而本测量方案是对标的比较式测量，在温度超出允许范围时，可通过在同温度下重新对标准件进行对标来降低温度造成的测量偏差。

一般生产线现场的室内正常温度为20 ℃，温差不会超过±20 ℃，由于生产线上的环境复杂多变，测量方案需根据实际线上的环境决定，可添加温度传感器对现场的温度进行实时检测，若现场温度在允许范围内，例如在20℃±5 ℃内，则内径尺寸变化量约为2.7 μm，方案中圆心坐标定位时的偏移量较小，可直接进行测量；若现场温度超出所允许范围，并暂时不可恢复正常测量环境，则重新进行对标，将该温度条件下的测量结果进行分类保存，以便后期复查。现阶段本系统的调试阶段是在秦川机床厂的恒温装配车间内进行，现场温度保持恒定(20 ℃)，对测量效果影响较小，后期在生产线上进一步调试时可将各个不同温度区间的测量结果分类储存并深入分析。

(2) 振动影响

针对现场振动的影响，采用机械隔振、电路隔离和软件滤波的方式进行降噪处理。机械隔振是采用大理石工作台、防护罩和隔振底座进行初步隔震处理，大理石长期天然时效、组织结构均匀、线胀系数小、内应力完全消失、不变形，因此精度高、刚性好、温度特性稳定，可有效阻尼来自地面的振动；电路隔离是在采集传感器信号的电路中，通过调理、隔离、滤波等进一步减小高频干扰信号；软件滤波指在软件中将采集到的传感器信号进行滤波处理，常用的滤波算法包括高斯滤波、平均滤波、中值滤波等,本文采用能较好地保持原始数据形貌、不容易产生失真的高斯滤波算法对传感器的初始采样数据进行滤波处理，函数表达式为

(10)

式中：λc为截止波长；a为常量；t为空间域变量。

3.3 传感器误差分析及补偿

本文采用国内制造传感器的代表性企业(中原量仪)生产的杠杆式电感传感器(JT-502A)，由于制造水平有限，其自身必会有一定的测量误差，根据参数资料可知，测量误差小于2 μm。因为位置度测量方案中使用15支传感器组成的测量系统会使测量误差叠加，从而增大位置度测量误差，所以采用软件补偿的方法将单支传感器的测量误差降低至最低，从而为多传感器测量系统对摆线轮圆周均布的轴承安装孔组位置度提供一定的精度保证。

电感传感器是基于电磁感应原理，利用线圈的自感或互感变化来实现非电量电测的一种装置。当电感传感器的测头检测到被测物体的位移时，测杆带动铁芯产生移动，线圈的电感或互感系数发生变化，将电感或互感信号通过引线接入测量电路并转换成电信号输出。对于制造成型的电感传感器，硬件的固有缺陷造成传感器的铁芯移动量与电感传感器的电压输出量为非线性，从而使电感传感器的测量误差有固定的变化规律[15]，下面通过实验进行验证并进行建模。

3.3.1 传感器标定实验及误差模型建立

标定实验系统由微动测量台架(BCT—5C)、传感器、高精度电感测量仪(电箱)、PCI-1711数据采集卡及工控机组成，如图10所示。电感传感器(JT-502A)为压簧式，可将传感器装夹在微动测量台架上，并与标准量块接触。首先，通过微动测量台架将横向的标准位移量转化为传感器测杆的位移量，传感器将输出的电压量送入电箱，然后在高精度电感测量仪(电箱)内将输入的电信号进行放大、整形处理后，通过数据采集卡将传感器的测量结果传输到工控机。

选取4组重复性实验的数据，分别用不同线型及标识表示，如图11所示。可以看出，传感器的测量误差变化趋势一致(电感器重复性误差小于等于0.3 μm)，验证了对电感传感器测量误差分析的结论，即制造成型的电感传感器的测量误差由硬件的固有缺陷造成，属于定值性系统误差。

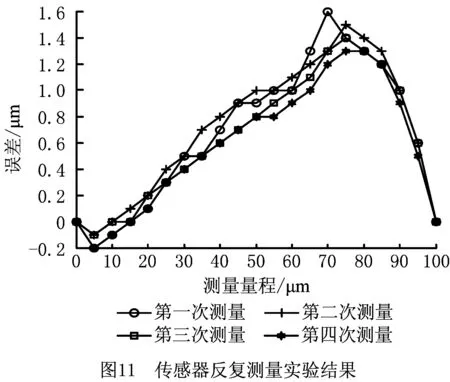
根据实验结果可以建立一种基于多项式插值函数的电感传感器测量误差补偿模型，以补偿电感传感器的测量误差。基于多项式插值函数的误差补偿模型基本形式为

Δf(x)=p0+p1·x+p2·x2+p3·x3+

p4·x4+p5·x5+p6·x6+

p7·x7+…+pn·xn。

(11)

式中：Δf(x)为电感传感器测量误差的拟合值；p0，p1，p2，p3，…，pn为待定未知数。

将传感器标定实验中第一次测量得到的传感器误差数据进行比较，最后选择拟合效果比较好的六次多项式插值法。将电感传感器测量误差的补偿模型编译成算法，写入本测试系统软件，重复传感器标定实验的步骤,对传感器测量结果进行误差补偿，即将式(11)带入式(12)进行计算。

F(x)=f(x)-Δf(x)。

(12)

式中：F(x)为补偿后传感器的示值；f(x)为补偿前传感器的示值；Δf(x)为传感器误差的拟合值。

3.3.2 传感器误差补偿效果

电感传感器误差补偿后的补偿效果如图12所示。可以看出，电感传感器的测量误差得到了有效的补偿，测量误差值从最大的1.6 μm降低至0.5 μm左右，并保持相对稳定，传感器的测量精度明显提高。需要注意的是，同种型号不同个体的传感器，其硬件制造会有偏差，经过实验验证，每支传感器的误差变化趋势并不相同，因此对位置度测量部15支传感器逐个使用同样方法进行误差补偿，各支传感器的测量误差均可降至1.0 μm以下，最小值约为0.5 μm。

对系统误差的各来源进行分析和补偿后，分别得到各误差项目：

导向套与被测孔的间隙误差δ1=0～1.84×10-4μm；

径向倾角误差δ2=0～7.37×10-4μm；

轴向倾角误差δ3=0～7.37×10-4μm；

传感器测量误差f1,f2,f3,…,f15=0～1.0 μm。

其中间隙误差、径向和轴向倾角误差很小，对总误差几乎没有影响，因此系统的综合误差

=2.0～4.0 μm。

下面进行实际实验，验证本测量系统的精度，以及误差分析的正确性。

4 实验结果

应用本文介绍的位置度检测设备和算法，在恒温车间内(20 ℃)对一个摆线轮(型号：320E)工件进行多次实验，并使用LeitzReference15.09.07 CMM(测量精度小于2 μm)的实验结果与本系统的结果进行对比，从而验证本系统的测量精度及准确性。实际测量数据如表1所示。

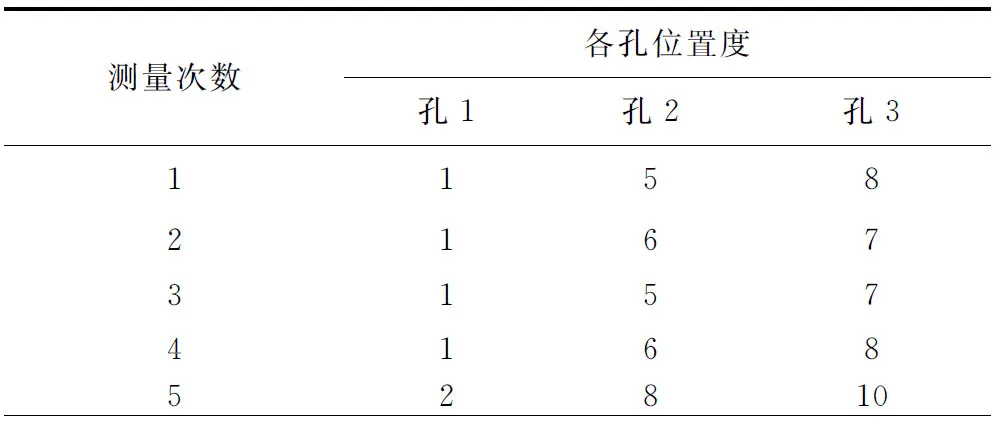
表1 本方法及CMM测量数据 μm

续表1

图13中用不同线型标示出各个孔的10次实验结果，CMM的测量结果在图中用虚线表示。

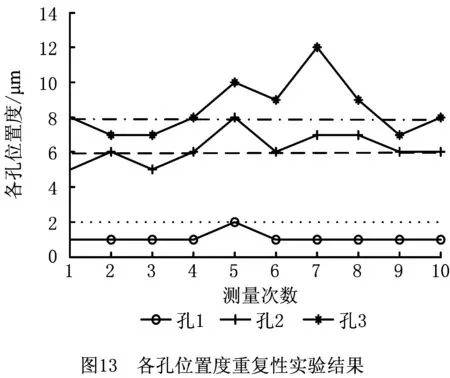
从测量结果的对比情况可以看出，孔1的测量误差小于等于1 μm，孔2的测量误差小于等于2 μm；孔3的测量误差小于等于 4 μm，即系统的误差在 4 μm以内，与第3章的误差分析结果一致(系统的综合误差在2.0 μm～4.0 μm之间)，说明系统的测量精度与之前的预测相差无几。

在误差分析和部分补偿后，本系统将影响测量误差的因素降至最低，测量误差小于等于4 μm的测量精度满足国内关节RV减速器生产线上对摆线轮轴承安装孔位置度的在线快速检测的要求。

5 结束语

本文针对工业机器人上关节RV减速器的关键零部件——摆线轮的轴承安装孔组位置度的在线检测问题，提出采用多传感器测量系统对其进行快速检测的方法。通过误差分析和补偿以及实际测量得到如下结论：

(1)应用多传感器测量系统并提出一种针对摆线轮轴承安装孔的孔组位置度算法，使用C语言将算法编译至测试软件中，使得测量节拍小于10 s，实现了对摆线轮圆周均布3个轴承安装孔组位置度的快速检测，满足生产线上的在线快速检测。

(2)对生产线现场的温度、振动等因素造成的影响进行分析并采取一定措施进行处理；对系统中的机构误差和传感器自身测量误差进行分析，发现机构误差对系统测量误差的影响可忽略不计；传感器自身测量误差在进行标定实验和误差补偿后，可将最大测量误差从1.6 μm降低至0.5 μm，最大限度地提高了系统对孔组位置度的测量精度。

(3)实验结果表明，该方法测量精度高，与CMM的测量结果进行对比验证表明，各孔的位置度最大测量误差小于等于4 μm，满足生产线上的检测要求。

参考文献:

[1] HUANG Xing, HE Wenjie, FU Yuanxiang. Summary of precision speed reducer of industrial robots[J]. Machine Tool & Htdraulics,2015,43(13)：1-6(in Chinese).[黄 兴,何文杰,符远翔.工业机器人精密减速器综述[J].机床与液压,2015,43(13)：1-6.]

[2] JI Shiming, HUANG Xihuan. Review of development and application of industrial robot technology[J]. Journal of Mechanical & Electrical Engineering,2015,32(1)：1-13(in Chinese).[计时鸣,黄希欢.工业机器人技术的发展与应用综述[J].机电工程，2015,32(1)：1-13.]

[3] WANG Tianmiao, TAO Yong. Research status and industrialization development strategy of Chinese industrial robot[J]. Journal of Mechanical Engineering,2014,50(9):1-13(in Chinese).[王田苗,陶 永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报，2014,50(9):1-13.]

[4] ZHANG Fumin, QU Xinghua, YE Shenghua. Multiple sensor fusion in large scale measurement[J]. Optics and Precision Engineering,2008,16(7)：1236-1240(in Chinese).[张福民,曲兴华,叶声华.大尺寸测量中多传感器的融合[J].光学精密工程,2008,16(7)：1236-1240.]

[5] SUN Jiwen, XI Lifeng, DU Shichang. Sensor allocation optimization for diagnosabil ity oriented to multi-station manufacturing system[J]. Computer Integrated Manufacturing Systems,2006,13(12):2441-2445(in Chinese).[孙继文，奚立峰，杜世昌.面向多工位制造系统可诊断性的传感器布置优化[J].计算机集成制造系统,2006,13(12):2441-2445.]

[6] MU Luxi, YIN Zhouping, XIONG Youlun. A global calibration method for multisensor metrology system[J].China Mechanical Engineering,2012,23(12)：1428-1432(in Chinese).[牟鲁西，尹周平，熊有伦.一种多传感器测量系统全局标定方法[J].中国机械工程,2012,23(12)：1428-1432.]

[7] LIU Zhigang, WANG Jinkuan. Interacting multiple sensor filter for sensor networks[J]. Acta Electronica Sinica，2012,4(4)：724-728(in Chinese).[刘志刚，汪晋宽.多传感器交互滤波算法[J].电子学报，2012,4(4)：724-728.]

[8] WECKENMANN A, KRMER P, HOFFMANN J. Manufacturing metrologystate of the art and prospects[C]//Proceedings of the 9th International Symposium on Measurement and Quality Control,2007:1-8.

[9] LI Bing, SUN Bin, CHEN Lei, et al. Application of laser displacement sensor in free-form surface[J]. Optical and Precision Engineering, 2015, 23(7): 1939-1947(in Chinese).[李 兵，孙 彬，陈 磊，等.激光位移传感器在自由曲面中的应用[J].光学精密工程，2015,23(7): 1939-1947.]

[10] CHEN Huacheng,WANG Boxiong,LUO Xiuzhi.Multi-sensor integrated automated inspection system[J].Proceedings of SPIE,2003,5253：528-531.

[11] ZHANG Weiguang, ZHAO Hong. Error correction method for three-dimensional measurement system with ,multi-sensor and linear-structure light[J]. Journal of Xi’an Jiaotong University,2011,45(6)：75-80(in Chinese).[张维光，赵 宏.线结构光多传感器三维测量系统误差校正方法[J].西安交通大学学报,2011,45(6)：75-80.]

[12] QIAO Xiangdong, LI Tao, YANG Tong, et al. On error cross-correlation and fusion algorithm for multi-sensor hybrid multiple model estimation[J]. Acta Electronica Sinica,2012,4(4)：804-810(in Chinese).[乔向东，李 涛，杨 仝,等.多传感器混合多模型估计的误差互相关性及其融合算法研究[J].电子学报，2012,4(4)：804-810.]

[13] ZHU Jia. Research on a multi axis inspection system based on integrated vision and touch sensing[D].Tianjin:Tianjin University，2010(in Chinese).[朱 嘉.基于视觉与触觉集成传感的多坐标组合测量系统的研究[D].天津：天津大学，2010.]

[14] SUN Bin, LI Bing. A rapid method to achieve aero-engine blade form detection[J]. Sensors，2015, 15(6):12782-12801.

[15] HE Yiming,SANG Nan, ZHANG Gangbing, et al. Principles and applications of sensors[M]. Nanjing:Press of Southeast University,2013:1-20(in Chinese).[何一鸣，桑 楠，张刚兵,等.传感器原理与应用[M].南京：东南大学出版社，2013:1-20.]