基于云模型与协同决策的FMEA耦合评估方法

安相华，蔡卫国+，宋晓杰

(1.大连海洋大学 机械与动力工程学院，辽宁 大连 116023; 2.大连理工大学 校园规划与管理办公室，辽宁 大连 116024)

0 引言

随着市场竞争的日益激烈及科技的高速发展，提高产品生命周期各阶段的质量可靠性、有效避免产品功能质量失效已经成为提高客户满意度、增加市场占有率的有效策略。失效模式与影响分析(Failure Mode and Effects Analysis，FMEA)是一种系统化的功能质量可靠性分析方法，该方法能够在故障发生前通过识别产品潜在失效模式的风险程度合理配置资源，并采取相应的干预措施来避免产品功能质量的失效,因此具有未雨绸缪的科学意义。FMEA在航空航天、船舶、汽车、医疗及服务等众多领域为决策者提供了前瞻性的指导信息，并得到了广泛认可和良好的发展[1]。

最广泛使用的FMEA方法是风险优先数(Risk Priority Number, RPN)计算法，RPN由发生频率O、严重度S和检测难度D 3个风险因子决定。标准的RPN计算方法在学术界和企业界一直存在争议[1-11]。业内学者归纳了标准RPN计算法的4个不足：①风险因子O，S，D的评价采用精确数值，忽略了评价专家知识的模糊性和不确定性信息；②风险因子O，S，D的相对重要度未能区别对待；③风险因子O，S，D的评价数值相乘后可能得到相同的RPN值，其结果无法反映风险的内涵和实质；④风险因子O，S，D将数值直接相乘后得到RPN值的方法缺乏鲁棒性，原因是RPN值对关键因素评价具有过高的敏感性。

为了解决上述问题，多年来国内外大量学者围绕RPN的计算方法进行了一系列深入研究，使该领域的研究呈现出百家争鸣的学术氛围。KOK等[2]采用感知计算方法处理风险因子O，S，D及其权重评价过程中的语言不确定性信息，提出基于区间二型模糊集(interval type-2 fuzzy sets)和Karnik-Mendel算法的群决策RPN计算方法；聂文滨等[3]基于模糊集合理论、最大熵原理和广义豪斯多夫距离等数学工具求得风险因子区间形式的风险顺序数,最后用逼近理想解排序法(Technique for Order Preference by Similarity to Ideal Solution，TOPSIS)对工艺失效模式风险优先数进行排序；AHMET等[4]基于模糊集理论处理风险因子评价过程中的模糊性问题，结合模糊层次分析法和TOPSIS进行RPN计算；WANG等[5]基于直觉模糊集合(Interval intuitionistic fuzzy sets)对不确定信息进行建模，提出一种集成网络分析法(Analytic Network Process，ANP)和复杂比例评价方法的FMEA新模型，进而实现了RPN的有效评价；王浩伦等[6]提出一种基于模糊语言变量和三角型模糊软集的FMEA风险群体决策评估方法；LIU等[7]为充分表达决策者的评价信息，建立了风险因子评价的模糊置信度模型，提出基于证据推理算法和灰色关联算子的RPN评价方法；安相华等[8]将模糊粗糙数用于解决RPN评价过程中的不确定性问题，引入改进的层次分析法和VIKOR算法实现RPN的初步排序，最后以复杂网络分析失效模式之间的关联性得到完善的RPN排序；CHANG等[9]通过建立失效模式与失效原因之间的网络关联关系，提出一种灰色系统和决策试验和评价实验室(DEcision MAking Trial and Evaluation，DEMATEL)集成的RPN评价方法；伍晓榕等[10]运用模糊集理论量化失效评估中专家经验和语言的模糊信息，提出基于模糊TOPSIS和DEMATEL模型的模糊关联FMEA方法；耿秀丽等[11]着眼于失效模式间关联关系对RPN计算的影响，提出基于犹豫模糊语言、VIKOR方法和DEMATEL模型相集成的FMEA风险评估方法。

就其本质而言，RPN的计算是一个不确定环境下的多属性群体决策过程。虽然现有文献对此进行了深入研究并取得了丰富的理论成果，但在一些基础性问题的处理上仍然有值得商榷或有待进一步改善的地方，具体如下：

(1)在FMEA过程中的不确定信息的处理上，各种类型的模糊集 (如直觉模糊集、区间二型模糊集、犹豫集等)被广泛用于不确定性信息的建模与处理并已取得显著的效果，但模糊集在信息建模的最后阶段都要将模糊信息通过去模糊化转变为精确数值，其间极有可能造成决策信息的失真。需要指出的是，随机性是不确定信息的重要成分，但各种类型的模糊集在随机性信息的处理上却尤显不足。

(2)失效模式的RPN计算是一个团队协同决策过程，如何融合不同专家的评价意见也是FMEA过程中的关键环节。传统方法都是对FMEA专家赋予权重后将各专家的评价值按线性关系相加得到团队评价值，再根据各失效模式的团队评价值进行排序。然而，各专家的认知程度和知识水平不同，传统方法缺乏必要的调解机制，不能有效处理专家意见的差异性和分歧性而难以满足团队决策的“协调性”要求。

(3)产品失效模式之间是彼此关联和传播，而非孤立存在的。文献[8-11]考虑到失效模式之间存在的关联关系，利用复杂网络或DEMATEL方法对失效模式之间的交互影响进行建模分析，不足之处在于没有从功能、物理等角度对失效模式的关联传播机理进行深层次挖掘，缺乏关于失效模式之间耦合传播的系统化分析方法，难以保证计算结果的客观性和科学性。

针对以上问题，本文提出基于云模型和团队协同决策的产品耦合传播FMEA方法。首先，在FMEA过程中采用云模型对具有模糊性和随机性的专家评价信息进行建模和处理，利用云模型的相关算法获得各个专家关于失效模式的RPN计算值；其次，引入广义证据理论对不同专家的评价结果进行融合，获得团队协同性的RPN决策结果；在此基础上，基于解析结构模型对失效模式之间的耦合关系进行分析并定义了耦合传播指数，进而对RPN进行修正并获得完善的失效模式风险程度排序结果；最后以大型数控机床的失效模式分析为例，对所提方法的有效性进行说明和验证。

1 基于云模型的决策机制

云模型(cloud model)，是信息工程领域科学家李德毅院士创新性提出的一种能够将定性概念描述与定量数值表达实现有机结合的不确定信息映射模型。相对于犹豫集、粗糙集和各种模糊集理论，云模型不但能够胜任不精确、模糊性和不完整信息的建模与计算，而且在处理随机性信息方面具有独特的优势，已经成为近年来研究热度较高的新型不确定信息处理理论，在知识发现、自动控制和决策等多个领域得到广泛应用[12-15]。

1.1 云模型的基本概念[12]

如果定量化数值论域U是由一系列精确数值x构成的非空集合，即x∈U，Y是描述U的定性概念，任意元素x(x∈U)是Y的一次随机实现，且x对Y的确定度y=μ(x)，满足μ(x)∈[0,1]是按照某种特定规律分别的随机数，即

μ:U→[0,1]，∀x∈U，x→μ(x)。

(1)

则x在U上的分布称为云(cloud)，数学上表示为Y(U)；每个二元关系数组(x,y)称为云滴(cloud drop)。

云模型在数学上可以利用数字特征的形式表示为Y(Ex,En,He)，其含义是Y所代表的定性概念可以通过云模型独特拥有的期望Ex(expected value)，熵En(entropy)，超熵He(hyper entropy)3个数字特征来刻画其中蕴含的模糊性和随机性。Ex是关于定性概念在统计学意义上的数学期望值，处于所有云滴构成的论域空间重心，是最能体现定性概念的数字特征；En是定性概念不确定性程度的度量,体现了Ex的模糊性和随机性，En的数值越大，表明定性概念的范畴越宽泛；超熵He是熵En的不确定性程度的度量，即En的熵，He同时反映了En的随机性和模糊性，决定了论域空间中云滴不确定度的密集聚合程度。关于云的3个数字特征的详细解释和定义可以参考文献[12]，限于篇幅，不再赘述。由于绝大多数科技和社会现象都符合正态分布规律，最具普适性和通用性的正态云模型成为理论研究和实际应用中的重点。以定义在区间[0,1]上的论域为例，其一维正态云分布如图1所示。

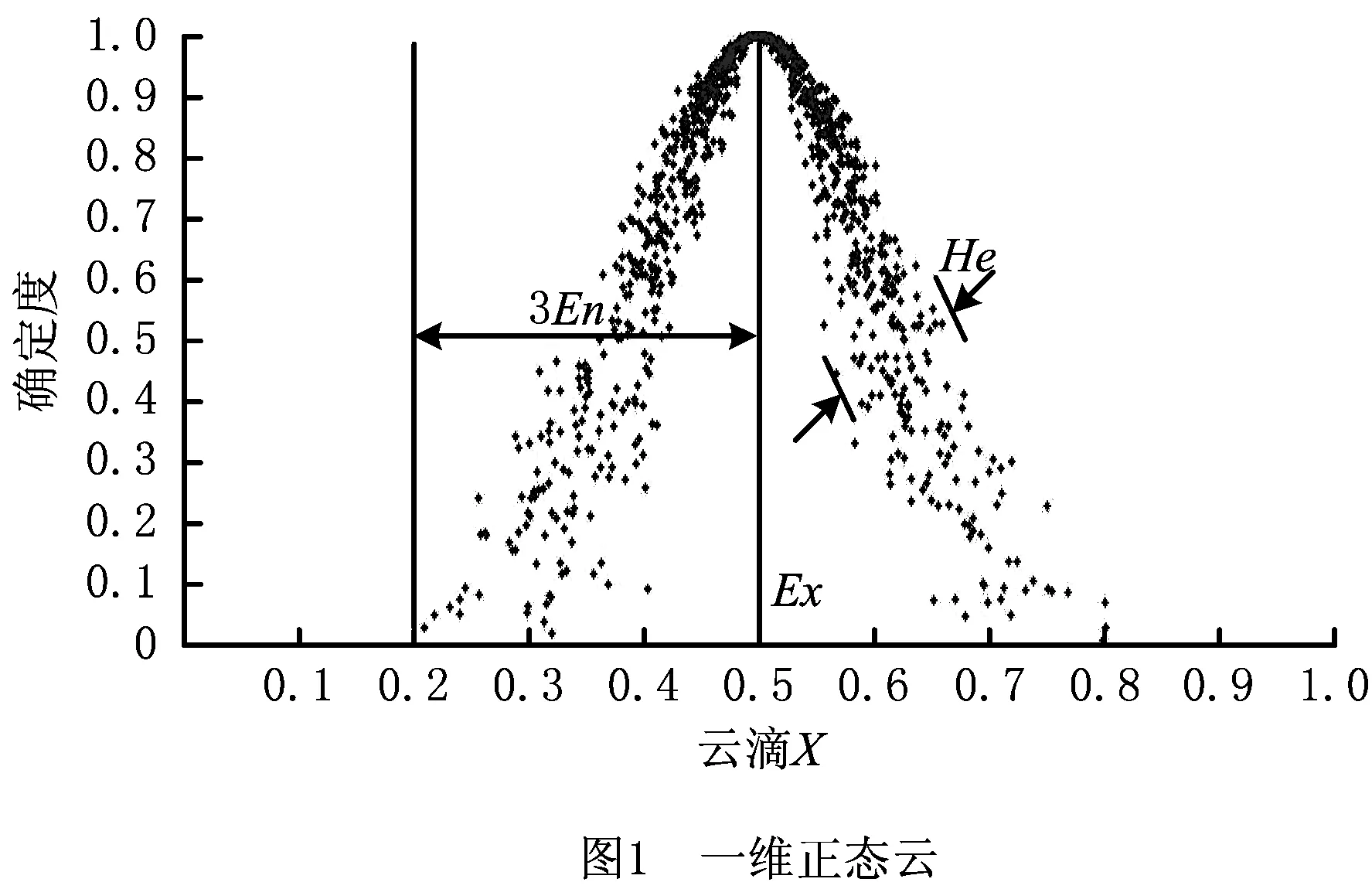
从云模型的定义可知，对于任意x∈U，x到论域[0,1]上的映射是一对多的变换，即x对U的确定度是一个概率分布而不是一个固定的数值。若x满足x～N(Ex,En′2)，其中En′～N(En,He2)，且x对Y的确定度满足

(2)

则x在论域U上的分布称为正态云(normal cloud)。本文FMEA的风险评估过程中均使用一维正态云模型。

1.2 云模型的定性语言变量转换

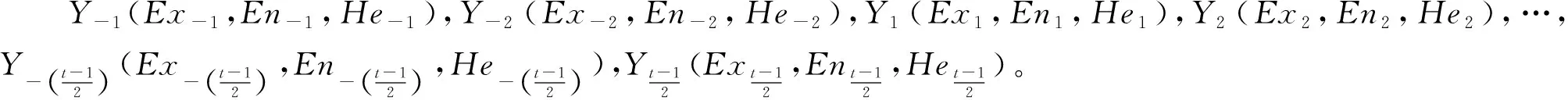
结合FMEA过程中风险等级评价的实际情况，本文拟采用7个语言标度来评价产品失效模式的各种风险因子，因此利用黄金分割法[12-14]生成七朵云的数字特征如下：

定义1设Yα(Exα,Enα,Heα)，Yβ(Exβ,Enβ,Heβ)为两朵云，则二者之间的Hamming距离定义为

(3)

2 基于云模型的风险优先数评估方法

采用由h个专家EXk(k=1,2,…,h)组成的FMEA团队对产品失效模式的风险优先数进行评估。在这一决策过程中，假设产品一共具有m项可能的失效模式集合FM，记为FM=(FM1,FM2,…,FMm)，其中FMi(FMi∈FM,1≤i≤m)是第i项失效模式。从现有文献的风险评估方式来看，多数学者都是只采用发生频率、严重度和检测难度3个传统风险因子进行评估，部分学者为了增加FMEA的应用范围，除了采用3个传统风险因子外，又增加了失效检测成本、失效影响程度、危险波及范围等其他种类的风险因子。因此，为了增加决策模型的适用范围和通用性，本文假定失效模式的风险因子共有n项，记作集合RF=(RF1,RF2,…,RFn)，其中RFj(RFj∈RF，1≤j≤n)为第j种风险因子，对应的权重集合为ω=(ω1,ω2,…,ωn)。因此，仅包括发生频率O、严重度S和检测难度D 3个风险因子的传统FMEA模型可以认为是本文模型(n=3时)的一种特殊情况。为了客观准确计算RPN，决策者引入云模型对风险因子的风险程度进行评价。

FMEA团队的h个专家以不确定环境下统一的语义变量集合{“非常高”、“很高”、“较高”、“一般”、“较低”、“很低”、“非常低”}作为定性概念来评价风险因子的风险程度，以论域U=[0,1]来映射7个定性的语义变量，因此生成关于语义变量的7朵云。FMEA团队的h个专家根据各自的知识和经验，利用7朵云表征失效模式的风险程度，得到专家EXk关于产品失效模式的云模型评估矩阵

RF1RF2…RFn

(4)

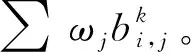
(5)

为了评估失效模式的风险程度，需要选取具有参照价值的理想点以便于后续计算，借鉴TOPSIS方法中理想解的方法和思想，定义理想云

(6)

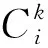
(7)

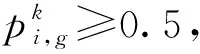
(8)

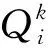
3 基于广义证据理论的协同RPN决策

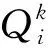
3.1 证据理论的基本概念

假定存在由q个互不相容的命题构成的集合空间Θ={H1,H2,…,Hq}，Θ为辨识框架。如果在Θ上存在映射函数M:2Θ→[0,1],且满足条件

(9)

式中：∅是空集，2Θ为Θ的幂集。则称M(A)是集合A⊆2Θ的基本概率分配(Basic ProbAbility Assignment,BPA)函数,表示所提供的证据能够证实命题集合A为真的可信度，如果M(A)>0,则称M为A的焦元。M(Θ)是Θ的BPA函数，M(Θ)作为特殊焦元是一种不确定性的概率化度量，即所提供的证据无法证实Θ中任意一个命题为真的概率。

在同一辨识框架上的两个独立证据源给出的焦元为M1(A)和M2(A),根据Dempster正交和范式⊕,可以将M1(A)和M2(A)按照式(10)和式(11)进行融合集结：

M1(A)⊕M2(A)=

(10)

K=M1(C)⊙M2(D)=

(11)

式中K称为规模化因子，其值反映了证据源之间冲突的大小。当焦元多于3个时，可按同样的方法进行递归融合集结。例如M1⊕M2⊕M3=M12⊕M3=M123，即先将M1和M2融合集结获得M12后，再将M12与M3按式(10)和式(11)进行正交加和，由此融合集结3个焦元得到M123。在辨识框架上，利用焦元可以定义命题集合A的信任函数Bel(A)和似真函数Pls(A)：

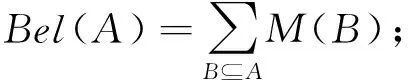
(12)

Bel(A)和Pls(A)分别表示置信程度的下限和上限。

3.2 基于广义证据理论的协同决策模型

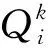
(14)

Mk(Θ)表示专家EXk确定失效模式集合风险排序的不确定程度，因为每个专家在计算失效模式的RPN时是采用云模型进行评价的，所以引入概率分布式的不确定性。云模型的熵和超熵都是不确定成分的重要来源，广义证据理论为分析这种不确定信息提供了一个可靠的渠道，而一般的评价方法均未考虑这种不确定性。根据广义证据理论的思想，在逻辑上定义

(15)

考虑到FMEA团队中不同评价专家具有不同的权重，对每个证据源的焦元进行修正，同时为方便计算，对两类焦元进行归一化处理并得到新的焦元：

(16)

(17)

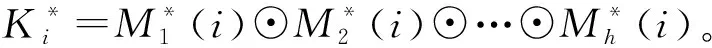
(18)

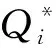
4 基于解析结构模型的风险优先数修正方法

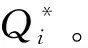
产品失效模式之间的耦合关系可以概括[20]为功能耦合、物理耦合、结构耦合、几何耦合和维修耦合：①功能耦合指不同失效模式在实现同一功能时的相互作用;②物理耦合指失效模式之间在能量和物质方面存在传递或交换的物理关系，如电流或力矩的传递或交换；③结构耦合指失效模式之间在产品的零部件结构或参数上的相互关系；④几何耦合主要体现在不同失效模式在平行度、垂直度、同轴度等方面的几何连接关系;⑤维修耦合可归纳为空间形位关系的耦合，涉及产生失效模式的零部件之间的联接、紧固和装配关系等，描述了产品生命周期各阶段需要维修保养时所涉及的装配性、拆卸性、维护性等。这5种耦合关系能够详细地描述产品失效模式的耦合作用机理。将这5种耦合关系解析为属性集{ATy|y=1,2,3,4,5}赋予产品的失效模式，其中：AT1表示功能属性，AT2表示物理属性，AT3表示结构属性，AT4表示几何属性，AT5表示维修属性。构建产品失效模式属性矩阵

AT1AT2AT3AT4AT5

(19)

式中Zi,y表示失效模式FMi的属性ATy。

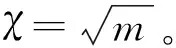
(20)

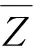
(21)

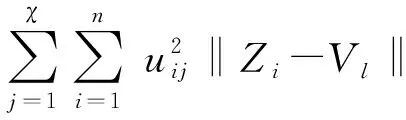
实验条件：785 nm激光器，光谱扫描范围为3 500～200 cm-1，功率为360 MW，激光波长为785 nm，输出时间为45 s。

(22)

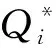
(23)

5 案例分析与应用

数控机床是将机械、电气、控制等多种技术融为一体的复杂机电系统。随着制造业的不断升级，客户对数控机床的加工精度、稳定性等性能提出了越来越高的要求，保障数控机床综合性能的关键便是失效模式与影响分析。本文以大型数控机床为研究对象来说明所提出方法的应用与实现过程。大型数控机床对安全可靠性和质量稳定性有极高的要求，FMEA团队根据数控机床的特点和实践经验识别26项主要的失效模式，如表1所示。

表1 数控机床失效模式信息表

FMEA团队由来自研发、生产、质检、维修、管理部门的5位专家组成，其权重分别为μ1=0.15，μ2=0.25，μ3=0.17，μ2=0.3，μ5=0.13。FMEA团队结合数控机床的特点，通过层次分析法获得发生

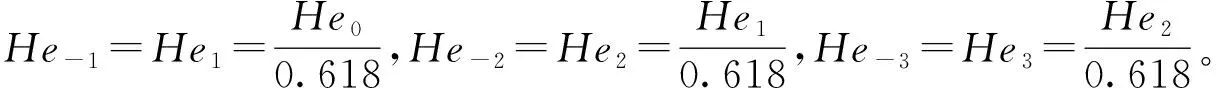
表2 单个专家的云模型评价信息表

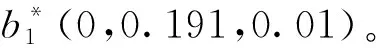
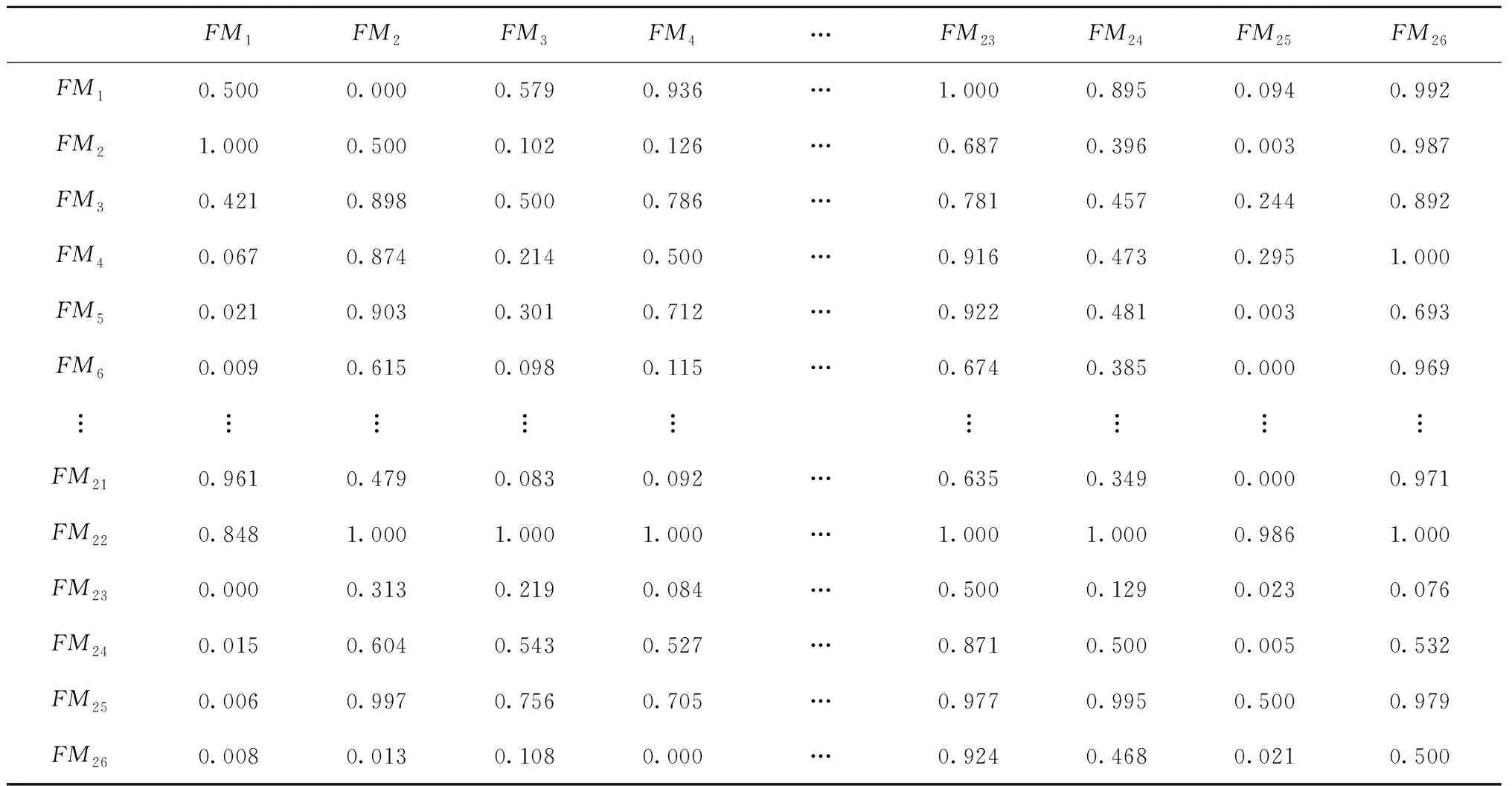
表3 风险优先数的成对比较矩阵

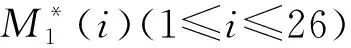
从数控机床的功能结构特点出发，利用文献[21]提出的基于层次分析法确定功能属性AT1、物理属性AT2、结构属性AT3、几何属性AT4、维修属性AT5在解析结构模型聚类过程中的各属性聚类影响因子分别为：η1=0.164 8，η2=0.235 8，η3=0.193 7，η4=0.142 2，η5=0.263 5。根据数控机床的每个失效模式与聚类影响因子之间关联关系数值分布的实际情况，将失效模式与聚类属性之间的关联关系通过0-1-3-5-9数值序列来表示不相关、弱相关、一般相关、强相关、极强相关等关联强度，进而构成失效模式聚类样本属性关联矩阵

则产品失效模式属性矩阵Z可以表示为关联矩阵Γ与聚类影响因子矢量[η1,η2,η3,η4,η5]的叉积，即[Zi,y]26×5=Γ⊗[η1,η2,η3,η4,η5]，具体数据如表4所示。

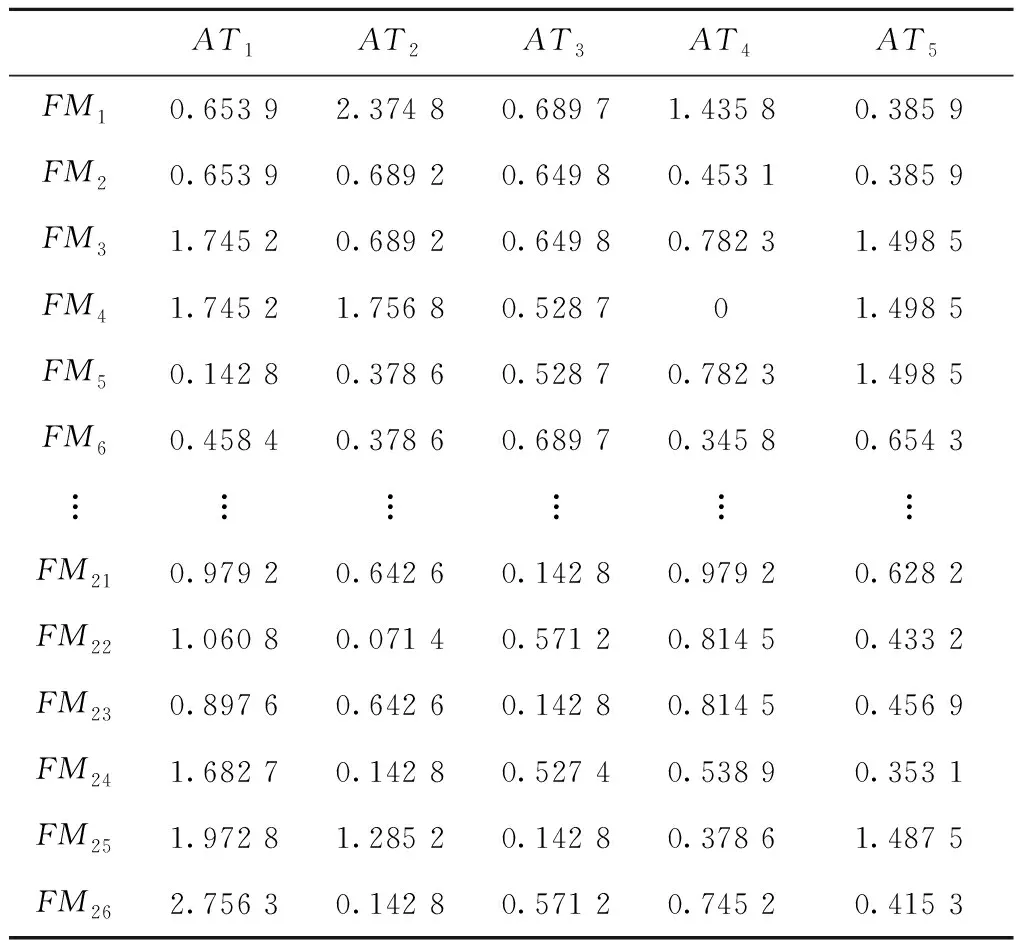
表4 数控机床失效模式属性矩阵

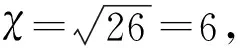
6 结束语

FMEA的RPN计算是一个蕴含多种不确定信息的团队协同群决策问题，而失效模式之间存在的耦合关联关系使这一问题更加复杂化。为了提高决策的科学性和真实性，从而达到保障FMEA发挥前瞻性和预防性的目的，本文采用逐层展开的方式提出基于云模型的不确定信息处理方法、基于广义证据理论的团队协同决策方法、基于解析结构模型的关联耦合分析方法三位一体的风险评估实施框架。最后，以大型数控机床的失效模式风险评估过程作为应用案例，表明了所提方法的灵活性、可行性和实效性。

相对于现有的FMEA方法，本文提出的基于云模型与协同决策的FMEA耦合评估方法具有以下优点：

(1)运用云模型建模专家对风险因子的评估信息，从模糊性、随机性两个角度充分保证专家在凭借自身知识进行决断时，既具有最大的主观能动性又不失严谨性，较一般不确定性信息处理方法更加贴近实际。

(2)以广义证据理论作为融合专家意见的手段打破了传统决策方法赋权平均的思维定式，能够模拟交际场景的谈判方式，通过专家之间的利益均衡和互相妥协获得协同性决策意见。

(3)基于解析结构模型的失效模式耦合传播分析方法，从失效模式发生耦合传播的内在机理这一全新视角出发，通过功能、物理、结构等属性建立失效模式之间的关联耦合模型，定量地为失效模式风险的传播性评估提供更客观、全面的参考依据。文中提出的决策模型不仅适用于FMEA过程，还对其他领域的决策问题具有参考价值。

参考文献:

[1] LIU Huchen , LIU Long, LIU Nan. Risk evaluation approaches in failure mode and effects analysis:a literature review[J]. Expert Systems with Application,2013,40(2):828-838.

[2] KOK C C, CHIAN H J, KAI M T, et al. A perceptual computing-based method to prioritize failure modes in faiture mode and effect analysis and its application to edible bird nest farming[J]. Applied soft computing,2016,49(C):4000-4015.

[3] NIE Wenbin, LIU Weidong, HU Kun, et al. Process failure risk assessment based on group decision-making and the generalized hausdorff distance[J]. Computer Integrated Manufacturing Systems,2015,21(9):2484-2493(in Chinese).[聂文滨，刘卫东，胡 坤，等.基于群决策和广义豪斯多夫距离的工艺失效风险评估[J].计算机集成制造系统,2015，21(9):2484-2493.]

[4] AHMET C K, MEHMET E L. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J]. Expert Systems with Applications，2012,39(1):61-67.

[5] WANG Lien, LIU Huchen, QUAN Meiyun. Evaluating the risk of failure modes with a hybrid MCDM model under interval-valued intuitionistic fuzzy environments[J]. Computers & Industrial Engineering,2016,102(11):175-185.

[6] WANG Haolun, XU Xiangbin, GAN Weihua. Using triangular fuzzy soft sets risk evaluation method in FMEA[J]. Computer Integrated Manufacturing Systems,2015,21(11):3054-3062(in Chinese).[王浩伦，徐翔斌，甘卫华.基于三角模糊软集的FMEA风险评估方法[J].计算机集成制造系统，2015，21(11):3054-3062.]

[7] LIU Huchen, LIU Long, BIAN Qihao, et al. Failure mode and effects analysis using fuzzy evidential reasoning approach and grey theory[J]. Expert Systems with Applications,2011,38(4):4403-4415.

[8] AN Xianghua, YU Jingbo, CAI Weiguo. Fuzzy rough FMEA evaluation method based on hybrid multi-attribute decision and correlative analysis[J]. Computer Integrated Manufacturing Systems,2016,22(11):2613-2621(in Chinese).[安相华，于靖博，蔡卫国.基于混合多属性决策和关联分析的模糊粗糙FMEA评估方法[J].计算机集成制造系统,2016,22(11):2613-2621.]

[9] CHANG K H, CHANG Y C, TSAI I T. Enhancing FMEA assessment by integrating grey relational analysis and the decision making trial and evaluation laboratory approach[J]. Engineering Failure Analysis,2015,31(6):211-224.

[10] WU Xiaorong, QIU Lemiao, ZHANG Shuyou, et al. Correlated FMEA method of complex system with linguistic vagueness[J]. Journal of Zhejiang University：Engineering Science,2013,47(5):782-789(in Chinese).[伍晓榕，裘乐淼，张树有，等.模糊语境下的复杂系统关联FEMA方法[J].浙江大学学报：工学版，2013，47(5):782-789.]

[11] GENG Xiuli, ZHANG Yongzheng. Improved FMEA approach for risk evaluation based on hesitant fuzzy set[J]. Computer Integrated Manufacturing Systems, 2017, 23 (2) :340-348(in Chinese).[耿秀丽，张永政.基于犹豫模糊集的改进FMEA风险评估方法[J].计算机集成制造系统,2017 , 23 (2) :340-348.]

[12] LI Deyi, DU Yi. Artificial intelligence with uncertainty[M].Beijing:National Defence Industry Press,2005(in Chinese).[李德毅,杜 鹢.不确定性人工智能[M].北京:国防工业出版社,2005.]

[13] ZHANG Longchang, YANG Yanhong, ZHAO Xuhui. SaaS decision-making method based on cloud model[J]. Acta Electronica Sinica,2015,43(5):987-992(in Chinese).[张龙昌，杨艳红，赵绪辉.基于云模型的SaaS决策方法[J].电子学报，2015,43(5)：987-992.]

[14] ZHAO Kun, GAO Jianwei, QI Zhiqiang, et al. Multi-criteria risky-decision-making approach based on prospect theory and cloud model[J]. Control and Decision,2015,30(3):17-23(in Chinese).[赵 坤,高建伟,祁之强，等.基于前景理论及云模型多准则决策方法[J].控制与决策，2015,30(3)：17-23.]

[15] REN Jian. Linguistic-stochastic multi-criterion decision-making method based on cloud model[J]. Computer Integrated Manufacturing Systems,2012,18(12):2792-2797(in Chinese).[任 剑.基于云模型的语言随机多准则决策方法[J].计算机集成制造系统，2012，18(12):2792-2797.]

[16] WANG Hongli, FENG Yuqiang. On multiple attribute group decision making with linguistic assessment information based on cloud model[J]. Control and Decision, 2005, 20(6): 679-685(in Chinese).[王洪利，冯玉强.基于云模型具有语言评价信息的多属性群决策研究[J].控制与决策, 2005,20(6):679-685.]

[17] QIU Dishan, HE Chuan, ZHU Xiaomin. Ranking method research of interval numbers based on probability reliability distribution[J]. Control and Decision,2012,27(12):1894-1898(in Chinese).[邱涤珊,贺 川,朱晓敏.基于概率可信度的区间数排序方法[J].控制与决策，2012，27(12):1894-1898.]

[18] PALASH D. Uncertainty modeling in risk assessment based on Dempster-Shafer theory of evidence with generalized fuzzy focal elements[J]. Fuzzy Information and Engineering,2015,7(1):15-30.

[19] WANG Ruihong. Multi-mode intelligent reasoning and fusion based on generalized evidence theory[D].Shanghai:Shanghai Jiao Tong University，2015(in Chinese).[王睿虹.基于广义证据理论的多模式智能推理与融合研究[D].上海：上海交通大学，2015.]

[20] DING Liping, TAN Jianrong, FENG Yixiong, et al. Construction of product module based on interpretive structure modeling and its optimization[J]. Computer Integrated Manufacturing Systems,2008，14(6):1070-1077(in Chinese).[丁力平，谭建荣，冯毅雄，等.基于解析结构模型的产品模块构建及其优化[J].计算机集成制造系统，2008，14(6)：1070-1077.]

[21] AN Xianghua, FENG Yixiong, TAN Jianrong, et al. Granularity decision method of product based on intelligent clustering algorithm[J]. Computer Integrated Manufacturing Systems,2010,16(4):689-745(in Chinese).[安相华，冯毅雄，谭建荣，等.基于智能聚类算法的产品粒度确定方法[J].计算机集成制造系统，2010，16(4):689-745.]