精彩从“变”中开始
——高三复习课函数变式教学应用举例
2018-06-30云南师范大学数学学院大姚一中
云南师范大学数学学院 大姚一中 玉 的
所谓的变式教学,就是教学中使用不同形式的直观材料或事例说明事物的本质属性,或者是变换同类事物的非本质属性特征以突出事物的本质特[2],从而使学生对某事物形成科学的概念。即教师通过引导学生思考解答某些数学问题之后,让学生在原问题基础之上进行观察、猜想,进而对原问题的内容、条件、结论进行相应的变换,并作进一步的探索,使得学生从不同的侧面深入思考数学问题的各种变化,并对这些变式题进行解答,以暴露问题的本质,揭示不同知识点的内在联系的一种教学设计方法[3]。变式教学通过让学生体验知识发生、发展过程,数学问题的结构和演变过程,从而培养学生解决问题的思维过程,以及创设暴露思维障碍情境,形成一种思维训练的有效模式。在我们教学中,教师常用的几种变式:如通过变换原式的背景,通过对原式的逆向思考构造变式,通过对原式的一般化构造变式,通过对原式的类比构造变式,通过对变式题构造变式,下面本人就从,“一题多解”“一题多变”“一法多用”等三个方面,来阐述高三数学函数如何进行变式教学。
一、“一题多解”
已知分段函数解析式与方程(或不等式),求参数的值(或范围)
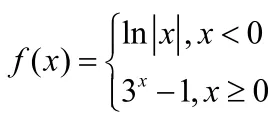
A.(- ∞,-1 ) ∪ (1 ,+ ∞ ) B.(- ∞,-1 ) ∪ ( 0,+ ∞)
C.(-1,0)∪ (01) D.(-1 ,0)∪ ( 0,+∞)
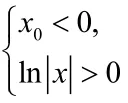
解法二:代入验证排除法
第一步:取x=-2,经检验成立,故排除C、D.

解法三:图像法
通过画图

观察图像可得 x ∈ (- ∞,- 1 )∪ ( 0,+ ∞ )【反思归纳】
(1)分段函数问题中,若给出函数值或函数值的范围求自变量的值或自变量的取值范围时,应根据每一段解析式分别求解,但要注意检验所求自变量的值或取值范围是否符合相应段的自变量的值或取值范围。
(2)涉及分段函数的不等式问题,应根据自变量的不同取值分类讨论转化为不等式组求解。
(3)当函数的解析式较为简洁时,可以通过画函数的图像,应用数形结合的思想解决问题。
(4)在选择题中,可优先考虑代入验证排除法,比较直接,省时、准确性强。
二、“一题多变”
例1、若函数f(x)是R上的减函数,且f(2a a- ) (A)0 解析:因为f(x)是R上的减函数且f(2a a- ) 所以2a a- >a, 所以2a a- >0, 所以a>2或a<0. 故选B. 变式1:若函数f(x)在R上为增函数,且f(2a a-) 解:()f x∵在R上是增函数 ∴ a2-a < a ⇒0 < a<2 变式2::若函数f(x)在(-1,1)上为增函数,且f(2a a- ) 【反思归纳】 (1)该类题的本质是利用函数的单调性,解不等式的问题,关注的是函数的定义域、单调区间、不等关系等; (2)变式时,通过改变单调区间,或单调性,解决不等式问题能让学生能更好的理解单调性的本质属性。 已知函数,若函数f(x)在(-2,-1)内为减函数,求a的取值范围。 已知函数,若函数f(x)在(-2,-1)内为增函数,求a的取值范围。 已知函数,若函数f(x)在(-2,-1)内存在减函数,求a的取值范围。 变式3: 若函数f(x)在(-2,-1)内上不单调,求a的取值范围。 变式4: 在区间[1,2]内至少存在一个实数x,使得f(x)<0成立,求a的取值范围。 变式5: 【变式意图】 (1)本题属于已知函数在某区间上的单调性求参数的范围的问题,先依据题意转化为 f′(x)≤0恒成立问题,然后再通过分离参数构造新函数,最后借助求新函数的最值求出参数的范围。 (2)在后面的变式1至变式4中,都围绕通过改变原题的条件,向结论过渡,其目的在于通过不同条件的变化,使学生能掌握应用转化与化归思想,类比的思想,顺利解决恒成立和能成立的问题,并能使学生的思维能力、知识的迁移能力得到提高。 (3)而变式5,与以上几个变式题有共同的地方都是解决恒成立问题,但如果依然希望通过分离参数来构造函数解决问题是非常麻烦的,此题必须通过移项构造新函数,然后转化为新函数的最值与0之间大小关系的恒成立问题来求解。设计的意图是,让学生体会构造函数的方法常有分离参数法和移项构造法。 变式教学通过让学生体验知识发生、发展过程,数学问题的结构和演变过程,从而培养学生解决问题的思维过程,以及创设暴露思维障碍情境,形成一种思维训练的有效模式。 (一)特殊值法、特殊思想在解决函数相关问题的应用 A.[-2,0)∪(0,2] B.(-1,0)∪(0,2] C.[-2,2] D.(-1,2] 解法一:直接法 要使原函数有意义,只需 解法一:特殊值法、代入验证排除法 观察选项先代-2, ln(-1)没有意义,排除A,C 再代0检验,ln1=0,分母为0,没有意义。故选D 【反思归纳】 以上两种方法相比较,第一种方法在等价转化时第三个条件容易考虑漏,而且解方程组时,比较容易出错。解法二,特殊值法,代入验证排除法,先观察选项,找出既方便运算又能排除选项的特殊值代入解析式中,根据需要满足的条件进行排除,从而快速的选出正确的答案,此法,既省时正确率又高。 【反思归纳】 (1)指对数的运算中,重点考察指对数之间的转化,先把指数式表示成对数式再利用对数的运算的性质、换底公式等进行化简运算,体现转化与化归的思想。 (2)特别注意对数运算性质的逆运算的应用。 (3)选择题、填空题,注意特殊值法、特殊思想的应用。 总之对于学生来说,变式教学可以使得学生在数学课上充分发挥主观能动性。数学变式教学符合学生的认知规律,有助于学生进行因材施教,在中国历史上孔老夫子最早提出因材施教,所以对不同水平的学生,采用有层次推进的变式,有助于学生获得抽象概括能力、推理能力、选择判断能力和自学能力。
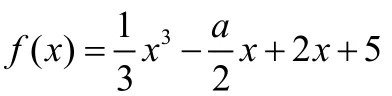

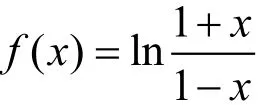
三、“一法多用”