数学实验教学的探究——几何画板在数学教学中的应用

◎张亦新

数学实验教学，是教师引导学生通过操作、实践、试验进行探索学习的教学形式.受传统的教学观念的影响，在数学课堂中，粉笔、直尺、圆规是数学老师的主要教具，而计算机投影PPT，只能起到静态放映的作用，必要的演算过程，都是靠粉笔书写，教师引导学生想一想，看一看，写一写.这些教与学解决了许多问题，但是有局限性，涉及变化运动，只能靠想象.现代教育技术为数学实验提供了动态视觉环境，如：几何画板，flash，Authorware等，它们既可以作图，又可以对图形进行旋转、平移、缩放、反射等变化，能够很好的展现动态数学，为数学实验教学及创新教学注入了无限活力.本文就用几何画板进行数学实验教学为课例，展现数学实验教学在探究活动中的作用.

1.课例函数y＝A sin（ωx+φ）的图象几何画板实验教学

几何画板作为实验教学的工具软件，不仅能制作出动态图形，还能显示几何图形中的各种度量关系.函数y＝A sin（ωx+φ）的图象这个课题，教学过程中，主要是让学生体会A、ω、φ三个量的变化，图形是如何变的，这种变化过程，几何画板能够很好的展现.因此本堂课采用几何画板教学，完美的让学生体会知识的产生，问题的解决，以及知识的迁移过程.以下为利用几何画板进行实验教学的探究过程.

2.1问题引入

2.1.1问题的产生

在物理和工程技术的许多问题中，都要遇到形如y＝A sin（ωx+φ）的图象（其中A、ω、φ是常数）.例如：物体作简谐振动时位移y与时间的关系；交流电中电流强度y与时间x的关系等都可用这类函数表示.从而有必要学习好y＝A sin（ωx+φ）这一类函数的图象.

2.1.2问题的变换

可以将上述问题分解为以下几个问题：

（1）函数y＝A sin x与函数y＝sin x的图象关系如何？A的意义如何？

（2）函数y＝sinωx与函数y＝sin x的图象关系如何？ω的意义如何？

（3）函数y＝sin（x±φ）与函数y＝sin x的图象关系如何？φ的意义如何？

（4）函数y＝A sin（ωx+φ）与函数y＝sin x的图象关系如何？

2.1.3学生猜想结论

让学生自身对三角函数的理解，猜想函数y＝A sin x与函数y＝sin x的图象关系、函数y＝sinωx与函数y＝sin x的图象关系、函数y＝sin（x±φ）与函数y＝sin x的图象关系，并将这三个关系结合起来，得到函数y＝A sin（ωx+φ）与函数y＝sin x的图象关系

2.2继续探讨

2.2.1学生实验

教师事先分别画出这些图形，把学生分成五组，让每组学生分别动手实验，拖动图形，进行观察，探求规律.商讨后，各组选定一代表提供问题的答案，学生反应热烈，问题的解决水到渠成.过程如下：

通过观察图象的变化，解答以下问题：

（1）函数y＝A sin x与函数y＝sin x的图象关系如何？A的意义如何？

（2）函数y＝sinωx与函数y＝sin x的图象关系如何？ω的意义如何？

（3）函数y＝sin（x±φ）与函数y＝sin x的图象关系如何？φ的意义如何？

2.2.2教师演示

教师将事先制作好的图象逐一演示.得到以下结论：

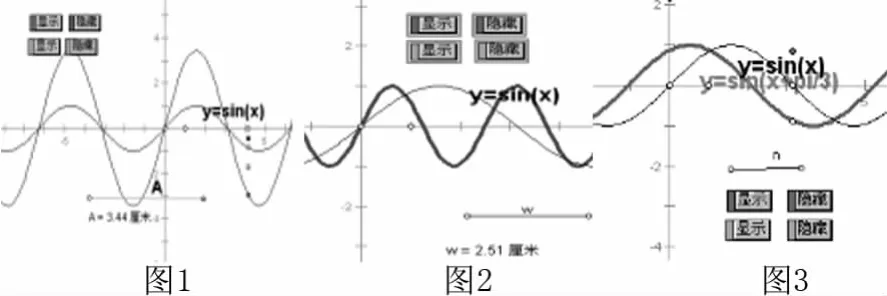
（1）观察图1，拖动A，得到结论：一般地，函数y＝A sin x（A＞0且A≠1）的图象可以看作是把y＝sin x的图象上所有的纵坐标伸长（当A＞1时）或缩短（当0＜A＜1时）到原来的A倍（横坐标不变）而得到的.

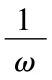
（3）观察图3，拖动n，改变φ，得到结论：一般地，函数y＝sin（x+φ），（φ≠0）的图象，可以看作是把y＝sin x的图象上所有的点向左（当φ＞0）时或向右（当φ＜0）时平行移动｜φ｜个单位而得到的.

2.3问题的引伸

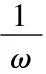
3.数学实验教学反思

在数学教学实践中，很少做数学实验，这些问题来自于应试压力，从素质教育出发，数学实验教学有利于学生的发展，这种探究过程对知识的产生与拓展完美呈现.对于实验教学有两点需要思考：一是对数学实验的认识不足，怕影响进度，影响成绩，但是如果不能够让学生参与探究过程，知识遗忘较快，效果也是不理想的；二是教师缺乏数学实验教学的经验，如何组织学生进行实验，如何引导学生总结实验过程中所产生的知识，需要老师不断尝试实验教学，总结经验，提高现代教育技术方面的技能.

有部分教师觉得数学教学中很有必要让数学实验进入课堂，但又缺乏数学实验的教学经验，因此，在教学中开展数学实验教学的课题研究，是很有必要的.实践性研究可分为两类：一类是数学实验的教学设计，另一类是一般操作问题的探究.

总之，数学实验课不仅能够使学生快速有效地掌握数学知识，更重要是能够提高学习的积极性，使学生乐于研究探索问题的起源和发展过程，有利于创造力的培养，体现学生的主体地位，有利于培养独立思考的品质和探索精神，培养学生发现问题、分析问题、解决问题的能力.

［1］刘胜利.几何画板课件制作教程［M］.科技出版社，2012年5月

［2］王浩华.数学实验与典型案例分析［M］.中国科技技术大学出版社，2017年8月