超声光栅法测量液体的体积弹性模量

李 聪，侯志栋，周丽霞

(中国石油大学(华东) 理学院，山东 青岛 266580)

超声光栅测量液体中的声速实验是经典的近代物理实验[1-2]，国内外已有很多人以此实验为依托，设计出了创新性实验, 利用超声光栅法测量溶液的声速，进而得到体积弹性模量. 曾育锋等通过实验得到食盐(NaCl)溶液浓度与其体积弹性模量成近似线性关系[3-4]；劳振花等分别研究了温度、矿化度、油水比对液体体积弹性模量的影响[5-7]；王寅观等则是对盐酸、氨水的液体体积弹性模量进行单独研究[8-9]. 本文主要研究糖类溶液体积弹性模量随溶液浓度的变化关系，并进行不同糖类之间体积弹性模量的比较，进而得到糖类溶液分子结构的一些性质.

1 实验原理

1.1 超声光栅测量声速原理

超声波在液体中以纵波的形式传播，在波前进的路径上，液体被周期压缩与膨胀，其密度产生周期性的变化，形成疏密波. 因为液体对光的折射率与液体的密度有关系，所以随着液体密度周期性地变化，其折射率也周期性地变化. 液体中折射率周期性变化的区域起到了与光学上平面光栅相类似的作用，当单色光垂直于超声波传播方向照射液体时，光会被液体衍射，这种实验装置称为超声光栅，这种效应称为声光效应. 在超声光栅的超声波频率不是很高的情况下，符合以下的光栅方程[10]：

Λsinθk=±kλ,k=0,1,2…

(1)

其中,Λ为超声波波长，θ是衍射角，k为衍射波级数，λ是光波波长. 当θ很小时，式(1)可以写为

Λθk≈±kλ,k=0,1,2，…

(2)

显然，只要已知入射光波波长λ，测出第k级衍射条纹对应的衍射角θ就可知道超声波波长，则透明液体中的声速v为

v=Λf,

(3)

式中f为超声波频率. 设入射光波长为λ，±k级衍射条纹间距为2dk，则第k级衍射条纹对应的衍射角θk为

(4)

其中F是望远镜物镜焦距，对于JJY-1型分光计，F=170 mm. 从超声光栅声速仪上读出当前超声波频率f，则根据式(2)和式(3)可得透明液体中的声速为

(5)

1.2 液体体积弹性模量与超声声速关系

液体媒质中的超声波平面波的波动方程与理想媒质中的平面波波动方程比较，可得到液体中的纵波声速为[3]

(6)

其中，B为液体体积弹性模量，v为声速，ρ为液体密度. 因此液体体积弹性模量的测量公式为

B=ρv2,

(7)

由(5)式和(7)式即可通过测量声速间接得到液体体积弹性模量.

2 实验结果与分析

2.1 溶液体积弹性模量的总体比较

实验采用如图1所示的WSG-I超声光栅声速仪完成，常见的钠光灯为光源，分别配置质量分数为3%，6%，9%，12%，15%，18%的葡萄糖溶液、果糖溶液、麦芽糖溶液，利用密度计对上述6×3组溶液进行密度测量，之后将这些糖类溶液分别置于水槽中， 观察其衍射条纹， 同时记录数据，最后，对数据进行处理，根据(5)式和(7)式计算出溶液的体积弹性模量. 表1给出了钠灯下不同浓度的葡萄糖、果糖、麦芽糖溶液中体积弹性模量的计算结果.

(a)光路系统

(b)面板图1 WSG-I超声光栅声速仪及实验装置图

表1 不同质量分数下葡萄糖溶液、果糖溶液、麦芽糖溶液中的体积弹性模量测量数据

根据表1数据绘制溶液体积弹性模量-质量分数的关系图如图2所示.

由图2可以看出，糖类溶液的体积弹性模量随溶液质量分数的增加而单调递增. 通过对比分析可知，对于单糖和二糖，相同质量分数下，单糖溶液的体积弹性模量整体上要大于二糖溶液的体积弹性模量，这是因为同一质量分数下，二糖的分子质量大，因而传播速度会减小，这与Parthasarathy经验规律是符合的[11-12]，从而计算的溶液体积弹性模量就会越小.

从麦芽糖的分子结构(图3)来看，1个分子麦芽糖可以分解为2个分子葡萄糖，麦芽糖分子中的两葡萄糖残基通过氧原子连接，因而很容易与溶液中的氢原子发生静电作用，形成氢键. 水合层的可压缩性将会降低，绝热压缩系数增大，溶液中水合层受干扰程度减弱[11]，则声速越小，绝热压缩系数β与声速、体积弹性模量的关系为[13]

(8)

体积弹性模量减小，与上述分析单糖和二糖的大小关系是相符的. 由此我们认为，随着糖类分子量的增加，溶液体积弹性模量逐渐减小.

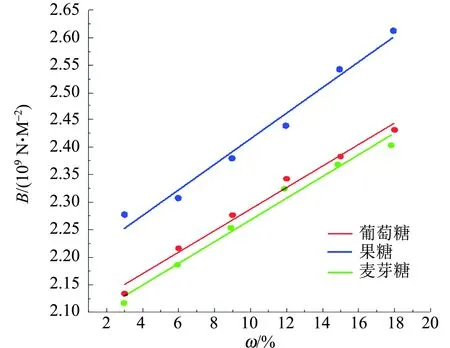
图2 体积弹性模量-质量分数关系图

图3 麦芽糖分子立体化学结构图

对于2种单糖溶液，相同的质量分数的果糖溶液的体积弹性模量要大于葡萄糖溶液. 原因可能是葡萄糖和果糖属于同分异构体，天然的葡萄糖多是吡喃型葡萄糖，而果糖既有吡喃式，也有呋喃式. 因此两者体积弹性模量的差异可能是由于果糖在水溶液中同时以呋喃环和吡喃环状结构存在而造成的[11]，由文献[14]可知，呋喃式结构比吡喃式结构更适合水分子.

2.2 3种糖类之间拟合关系的比较

对葡萄糖、果糖、麦芽糖溶液体积弹性模量-质量分数进行数据拟合，得到3种糖类的拟合公式为

B葡萄糖= 0.019 51ω+2.092,B果糖=0.023 05ω+2.186,B麦芽糖=0.019 54ω+2.071.

根据拟合公式可知，糖类溶液体积弹性模量随溶液质量分数变化基本呈线性关系. 通过其斜率可知，果糖溶液的体积弹性模量随溶液质量分数变化率最大，其次是麦芽糖、葡萄糖. 究其原因，如前文中解释，麦芽蔗糖分子中的两葡萄糖残基通过氧原子连接，因而很容易与溶液中的氢原子发生静电作用，形成氢键，导致体积弹性模量的变化率减小；而对于果糖和葡萄糖，主要原因是二者分子结构不同，葡萄糖多是吡喃型，而果糖在水溶液中同时以呋喃环和吡喃环状结构存在，呋喃式结构比吡喃式结构更适合水分子，从而导致果糖的变化率要大于葡萄糖.

3 结 论

采用超声光栅法，讨论了质量分数对溶液体积弹性模量的影响情况. 糖类溶液的体积弹性模量随着溶液质量分数的增加是单调递增的；对于同一质量分数的溶液，随着C原子的增加，溶液的体积弹性模量逐渐变小；对于属于同分异构体的单糖溶液，分子的结构会影响其溶液的体积弹性模量，如葡萄糖和果糖，葡萄糖多是吡喃型，而果糖既有吡喃式也有呋喃式，在水溶液中同时以吡喃式和呋喃式2种形式存在，呋喃式结构比吡喃式结构更适合水分子，这使得同质量分数果糖溶液的体积弹性模量要大于葡萄糖溶液；从溶液的体积弹性模量变化率的角度而言，果糖溶液变化率最大，其次是麦芽糖、葡萄糖.

参考文献：

[1] 刘雪凌,唐志列,阮立锋. 超声光栅的光栅常数理论研究[J]. 大学物理,2013,32(5):24-26.

[2] 丁冠阳,唐军杰,王爱军. 超声光栅测声速实验方法的探索[J]. 大学物理实验,2014,27(6):64-66.

[3] 曾育锋,涂辉. 超声光栅测量液体体积弹性模量实验研究[J]. 实验技术与管理,2012,29(4):53-54.

[4] 王锁明,侯彬,朱二旷,等. 基于超声光栅衍射的液体密度测试[J]. 物理实验,2013,33(4):41-43.

[5] 劳振花,姜兆波. 液体体积弹性模量与矿化度关系测量实验研究[J]. 科学技术与工程,2009,9(13):3776-3778.

[6] 劳振花,姜兆波. 液体体积弹性模量与温度关系测量实验研究[J]. 科学技术与工程,2009,9(13):386-390.

[7] 劳振花. 液体体积弹性模量与油水比关系测量实验研究[J]. 科学技术与工程,2010,10(9):2148-2150.

[8] 王寅观,邵良华. 氨水体积弹性模量的超声检测研究[J]. 声学学报,1996(4):625-631.

[9] 王寅观,邵良华. 盐酸体积弹性模量的超声检测研究[J]. 同济大学学报(自然科学版),1995(2):169-174.

[10] 王殿生,周丽霞,亓鹏,等. 物理实验教程·近代物理实验[M]. 青岛：中国石油大学出版社,2016.

[11] 刘东红,叶兴乾,吴昭同. 超声波对糖溶液物化特性的研究[J]. 中国食品学报,2005,5(4):11-16.

[12] Suryanarayana C V. Propagation of ultrasonic waves in liquids: A new model [J]. Ultrasonics, 1992,30(2):104-106.

[13] Alagar M， Ponnusamy M， Krishnasamy V. Studies on ultrasonic properties of different series of liquid system [J]. Ultrasonics, 1990,28(11):386-390.

[14] Pal A, Kumar H. Thermodynamic parameters of binary liquid mixtures of some-alkoxyethanols with water at 298.15 K deduced from ultrasonic speed and viscosity data [J]. Physics and Chemistry of Liquids, 2003,41(4):405-421.