面向筒类舱段自动装配的两点定位调姿方法

金贺荣 刘 达

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

2.燕山大学先进锻压成型技术与科学教育部重点实验室，秦皇岛，066004

0 引言

在火箭、导弹、卫星等航天器的生产制造过程中，舱段对接是航天器总装的核心工序，“部装-总装”是常用的生产模式，即首先完成对接舱段的组装生产，然后在总装时实现各舱段之间的对接［1］。自动对接技术是非人为干涉的自动化对接过程［2］，实现对接舱段自动调姿可提高航天器的装配效率和品质均一性，合理的调姿方法是实现舱段自动调姿对接的关键。

在现有的舱段自动调姿技术中，多是采用并联机构［3⁃5］或可等效为并联机构的若干三坐标定位器组成的位姿调整系统来实现部件的自动调姿。易旺民等［6］提出采用6⁃SPS并联机构的位姿控制与力控制方式共同实现对接；蒋君侠等［7⁃8］设计了基于三坐标POGO 柱的适用于三段大部件对接的柔性装配平台，并对调姿平台进行了结构优化；黄翔等［9］发明了基于3⁃2⁃1随动式定位器的飞机部件位姿调整方法，保证飞机部件在调姿过程中不会出现非刚体性运动。在对调姿方法的研究中，张斌等［10］对可等效为6自由度冗余驱动并联机构的三坐标支撑柱的大型刚体位姿调整系统进行了轨迹规划，并对各驱动关节设置了约束条件，使调姿过程较为平稳，但冗余驱动存在一定内力，会对弱刚性构件刚度产生影响，而设定的约束条件并没有考虑这一点；刘继红等［11］给出基于关键特征的大部件对接位姿调整技术，提高了装配效率，但大部件对接与间接关键特征的提取过程较为复杂，且没有提出一种基于关键特征的大部件对接轨迹规划方案，仍需一定的人工参与；朱永国等［12］提出了飞机装配高精度测量控制网的构建方法，测得的机身各部分坐标系可转换成任意局部坐标系下的坐标，增加了机身的位姿测量与表达的灵活性；王少峰等［13］提出了一种基于精密三坐标定位器四点支撑的大型飞机机身壁板的装配位姿调整方法，将调姿过程分解为位置与姿态2个调整阶段，从而降低了多轴协调控制的难度，但在机身姿态调整过程中仍需多轴协调控制，该系统动力学模型是一个多解的冗余驱动问题，反解较为麻烦；崔学良等［14］针对大尺寸弱刚性构件对接装配系统进行轨迹规划，将定位器驱动轴分为非冗余驱动和冗余驱动两组，通过运动学正反解映射模型对非冗余驱动轴进行同步规划，对控制水平要求较高；应征等［15］以四定位器调姿机构为研究对象，建立调姿机构的系统动力学控制方程，解决了冗余并联机构的正动力学建模问题，但基于四定位器调姿机构的轨迹规划和调姿稳定性问题有待继续研究。采用上述基于并联机构或可等效为并联机构的调姿方法可以实现舱段的自动对接，但是并联机构由于其结构的复杂性以及运动学和动力学问题的非线性，使得并联机构的建模和控制都非常困难［16］，导致舱段对接效率较低且容易出错。位姿调整过程的稳定性和调整后的精准度都直接影响装配后舱体的工作性能。

目前基于关键点或关键特征的调姿方法，一般是通过检测调姿对象的关键特征或是预先固定在其上的若干关键点位置来得到调姿对象在全局坐标系下的位姿矩阵，并采用插补法实时进行轨迹规划，调姿对象在3个坐标上的姿态偏差同时调整，算法较复杂，如文献［17］基于鞍点规划理论的位姿评估模型，通过激光跟踪仪系统测量机翼上特征点的坐标位置,以及用直线位移传感器测量机翼水平测量点的高度来对机翼位姿进行评估，得到了机翼的准确位姿，但设置特征点过多，且关键特征的提取又较为复杂［11］，增加了调姿过程的复杂性。为降低调姿机构的控制难度与简化调姿算法，本文提出一种两点定位调姿法，并进行了仿真分析。

1 对接舱段位姿标识

标识对接舱段在空间内的位置和姿态，在装配空间内建立全局坐标系OXYZ作为基准，结合舱段结构特点建立参考坐标系O1X1Y1Z1。O1X1Y1Z1固定在舱段对接面上，原点O1为对接面的圆心，X1轴过舱段定位销孔的圆心O2，Z1轴与舱段轴线重合，如图1所示。

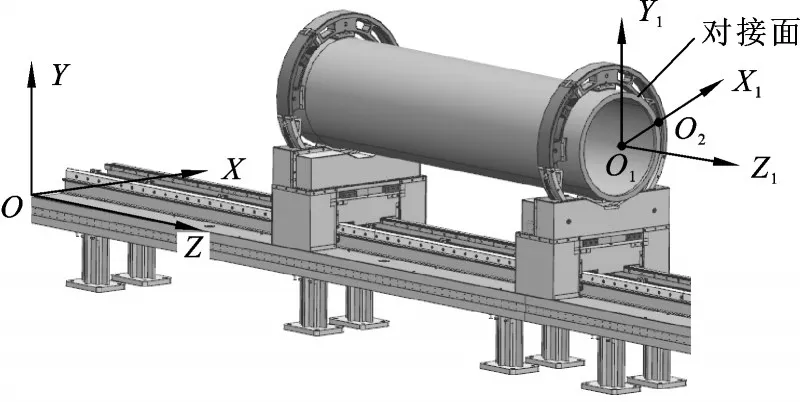
图1 装配坐标系Fig.1 Assembly coordinate system

局部坐标系转换到全局坐标系的旋转矩阵R和平移矢量T是唯一的［18］，对接舱段的空间位姿可以用矢量表示为对接舱段在参考坐标系内的位姿，用矢量N表示为

其中，(XO1,YO1,ZO1)T是O1点在OXYZ内的位置矢量，α、β、γ为O1X1Y1Z1相对于OXYZ的偏转角、俯仰角、横滚角，如图2所示。

图2 舱段姿态角Fig.2 Cabin attitude angle

2 两点定位调姿法

在航天器舱段对接装配过程中，对接舱段的理想位姿为O1X1Y1Z1与OXYZ平行且同向，即α、β、γ均为0，舱段的位姿调整即消除舱段的偏转偏差、俯仰偏差、横滚偏差以及调整舱段在X、Y、Z方向上的位置。为实现对接舱段的位姿调整，本文结合对接舱段的结构特点，提出一种两点定位调姿法，通过控制对接舱段表面两点的位置实现舱段位姿的调整。

在对接舱段的舱体表面定义Q1、Q2两个位置控制点，位置见图3。过Q1、Q2的直线与舱段轴线平行，Q1点与舱段固定在一起，舱段可随Q1点一起运动，Q2点对舱段起支撑和限位作用，Q2点始终与舱体表面接触，舱体可沿Q2点滑动。Q1点和Q2点沿Z向的距离为l1，Q1点到舱段对接面的距离为l2，Q1点和Q2点到舱段轴线的距离为l3。l2为固定值，不随舱段的不同而变化；l为舱段的长度，舱段不同，l值不同。l1=l-2l2。

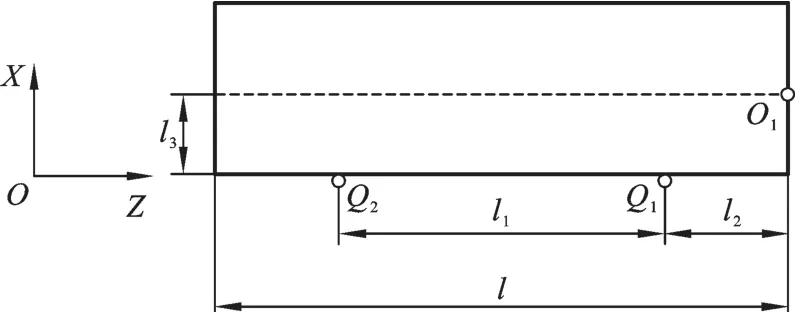
图3 Q1、Q2点位置示意图Fig.3 The position ofQ1，Q2

在偏转调姿过程中，对接舱段的偏转角为α，则Q1点和Q2点在X方向上存在ΔX1=l1tanα的位置偏差。消除对接舱段的偏转偏差，Q2点保持固定，Q1点沿X方向水平移动ΔX1的距离，在Q1点的运动过程中，对接舱段随Q1点运动，由于Q2点对舱段的限位作用，对接舱段沿Q2点滑动，并绕Q2点转动。偏转调姿过程见图4。

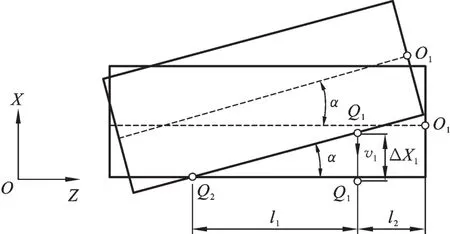
图4 偏转调姿原理图Fig.4 Deflecting attitude principle

在对接舱段的偏转角由α变为0的过程中，需要保证Q1点和Q2点的位置精度。对接舱段几何形状简单，位置控制点数量少且分布规律。采用在对称位置设置冗余测量点的方法来补偿控制点偏差，进而保证l1的值在偏转调姿过程中变化趋近于零。

要使得对接舱段以规划好的理想轨迹fα（t）实现偏转调姿，Q1点的运动速度v1应满足：

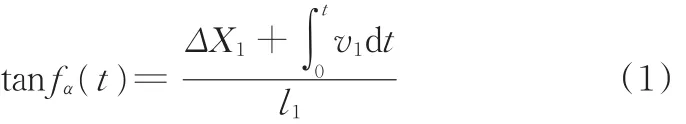
对式（1）求导得

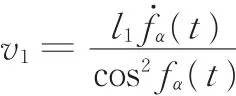
式中，ḟα(t)为对接舱段绕Y轴旋转角速度，记为ωα，角加速度记为 αα。

Q1点的动态坐标值为

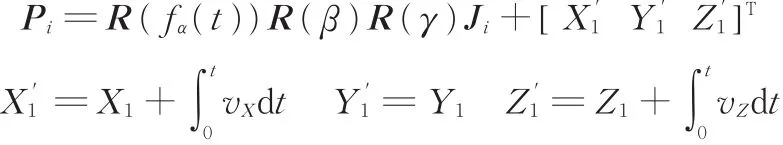
式中，Pi为Q1点的动态坐标值；R为局部坐标系转换为全局坐标系的旋转矩阵；Ji为Q1点在局部坐标系内的位置矢量；vX和vZ分别为O1点在X、Z方向上的运动速度函数。

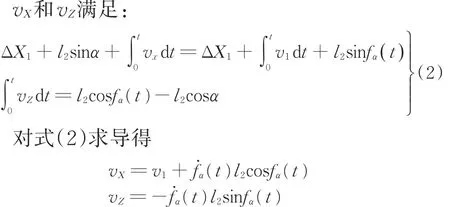
对接舱段俯仰调姿过程中，对接舱段的俯仰角为β，则Q1点和Q2点在Y方向上存在ΔY1=l1tanβ的位置偏差，Q2点保持固定，Q1点沿Y方向移动ΔY1，消除对接舱段的俯仰偏差，俯仰调姿过程见图5。在对接舱段的俯仰角由β变为0的过程中，在对称位置设置冗余测量点来补偿控制点偏差，l1的值在俯仰调姿过程中变化趋近于零，Q1点的运动速度满足下式可实现舱段按照俯仰调姿轨迹fβ（t）完成调姿：

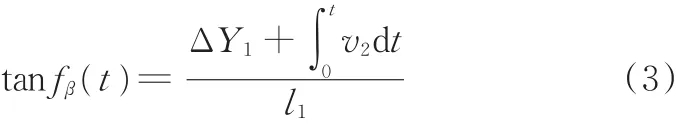
对式（3）求导得

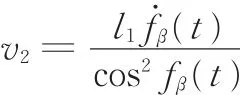
式中，ḟβ(t)为对接舱段绕X轴旋转角速度，记为ωβ，角加速度记为 αβ。

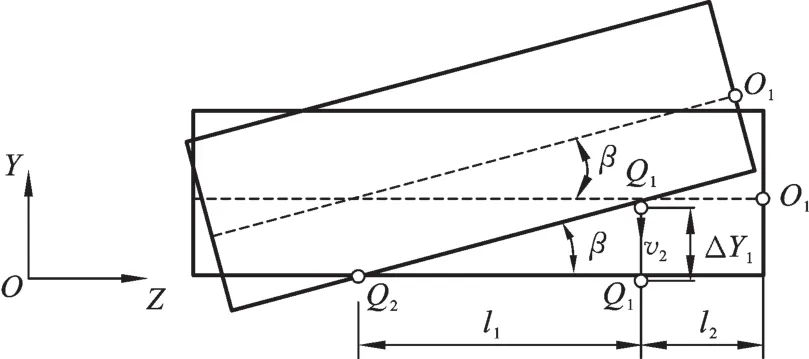
图5 俯仰调姿原理图Fig.5 The principle of pitching attitude

横滚调姿过程中，对接舱段的横滚角为γ。Q2点保持固定，Q1点绕舱段轴线旋转γ，则舱段绕自身轴线旋转γ，冗余测量点补偿Q1点的位置偏差，在XY平面内Q1点和Q2尽可能重合，横滚调姿过程见图6，横滚调姿轨迹fγ(t),Q1点绕舱段轴线旋转的角速度为 ḟγ(t)，记为 ωγ，角加速度记为αγ。

图6 横滚调姿原理图Fig.6 The principle of tilting attitude

对接舱段的姿态调整到位后，对接舱段的局部坐标系与全局坐标系平行，但是待对接的移动舱段和固定舱段仍不同轴，在X、Y方向上存在位置偏差，需调整移动舱段在X、Y方向上的位置。

使Q1点与Q2点同步沿X方向运动ΔX，带动移动舱段在X方向运动ΔX，以消除移动舱段X方向的位置偏差ΔX。使Q1点与Q2点同步沿Y方向运动ΔY，带动移动舱段在Y方向运动ΔY，以消除移动舱段Y方向的位置偏差ΔY。移动舱段在X、Y方向上与固定舱段的位置偏差消除后，移动舱段的轴线便与固定舱段的轴线同轴，达到可对接状态。对接舱段在X、Y方向进行位置调整时，Q1点与Q2点在相应方向上同步运动的速度为

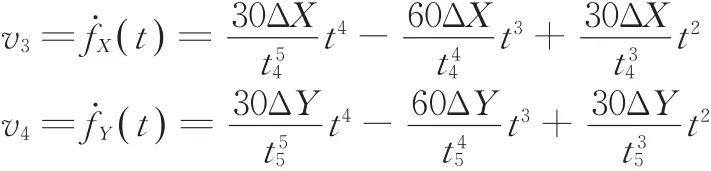
移动舱段的位姿调整到位后，使移动舱段沿全局坐标系Z方向运动ΔZ，就可完成与固定舱段的对接。Q1点与Q2点在Z方向上同步运动的速度为

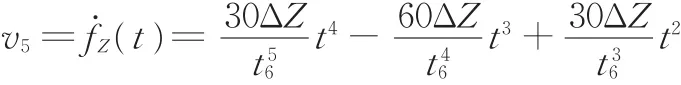
Q1点与Q2点在Z方向上同步运动的加速度记为a5。Q1点的动态坐标值为

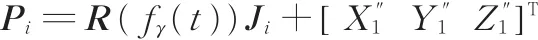
对接舱段在X、Y、Z方向进行位置调整时，Q1点的动态坐标值

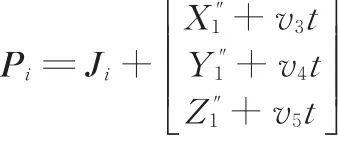
3 调姿运动轨迹规划

舱段调姿过程中初始与终止状态需满足以下约束条件：

位姿约束

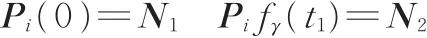
速度约束

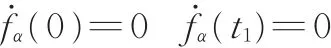
加速度约束

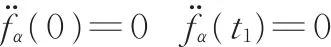
式中，t1为偏转调姿时间；N1为偏转调姿初始时刻舱段位姿；N2为偏转调姿终止时刻舱段位姿。

轨迹规划一般分为粗插补和精插补两步，为避免调姿过程中装配系统受到柔性和刚性冲击，在粗插补时采用S型速度曲线对调姿系统各驱动轴进行轨迹规划［14］，为保证调姿过程平稳、连续、无冲击，即要得到光滑的速度与加速度曲线，且将调姿运动轨迹方程代入上述约束后能解得全部未知参数，便于调姿过程稳定性分析，本文采用五次多项式轨迹对舱段进行调姿轨迹规划。以偏转调姿为例，在对舱段进行偏转调姿时，舱段偏转角的变化轨迹表示为

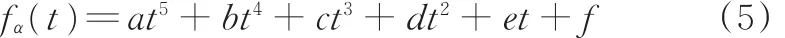
将上述约束条件代入式（5)得

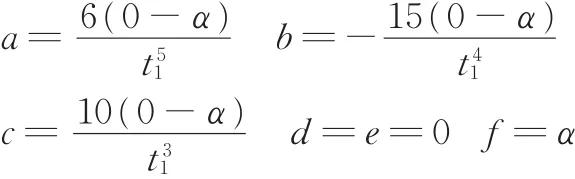
令Δα=0-α，可得偏转调姿的运动轨迹为

式中，Δα为偏转调姿过程中的偏转角变化量。

同理，可求得俯仰调姿、横滚调姿和位置调整的运动轨迹为

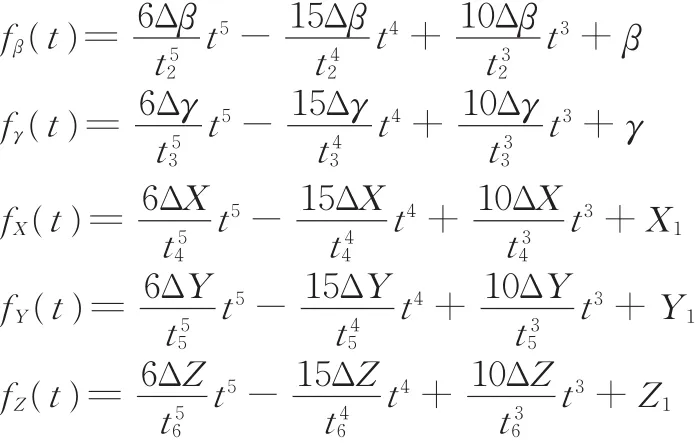
式中，t2、t3、t4、t5、t6分别为俯仰调姿时间、横滚调姿时间和X、Y、Z方向位置调整时间；Δβ、Δγ、ΔX、ΔY、ΔZ分别为俯仰调姿、横滚调姿和X、Y、Z方向位置调整过程中的位姿参数变化量。

4 调姿稳定性评价

最优时间法以满足调姿后状态所耗时间最短为目标［19］，但对于体积较大的舱段，调姿过程的稳定性同样重要。要想使对接舱段调姿过程平稳，对接舱段在姿态调整时的角加速度以及位置调整时的加速度绝对值应尽可能小。

对接舱段在姿态调整过程中的角加速度为

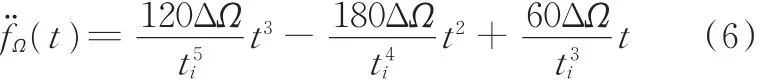
式中，ΔΩ为对接舱段姿态角α、β、γ调整量，i=1,2,3。

对接舱段质量较大，当对接舱段满足下式时对接舱段运动平稳：

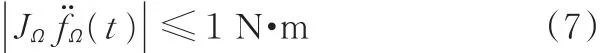
式中，JΩ为姿态调整过程中对接舱段转动惯量。

由函数极值定理［20］可得，当时角加速度取得极值，即

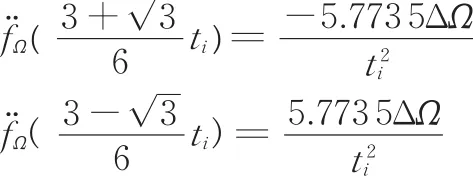
在［0 ti］时间段内，由函数最大值定理可得将式（8）代入（7）可得

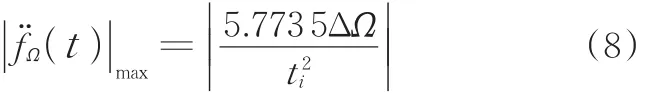
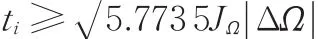
调姿时间取ti的最小整数值。

对接舱段在位置调整过程中的加速度

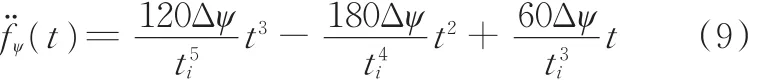
式中，Δψ为对接舱段在X、Y、Z位置调整量，i=4,5,6。

对接舱段在X、Y方向的位置调整满足下式时对接舱段运动平稳：

式中，m为对接舱段的质量。

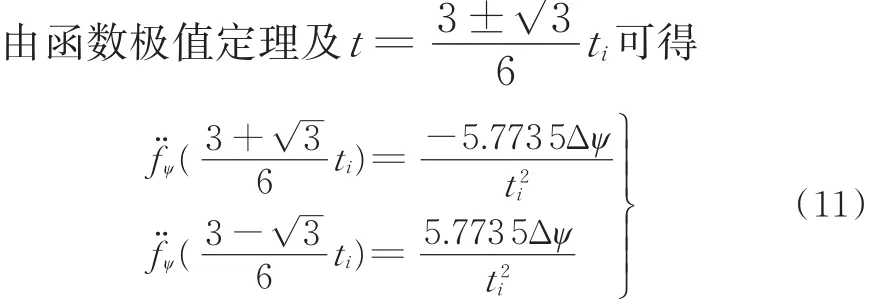
在［0 ti］时间段内，由函数最大值定理可得

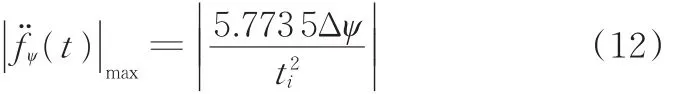
将式（12)代入式（10)可得

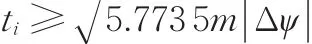
X、Y方向位置调整时间取ti的最小整数值。

对接舱段在Z方向的位置调整距离较大，应兼顾装配效率与稳定性，当对接舱段的运动满足下式时对接舱段运动平稳：

所以Z向调整时间t6满足:

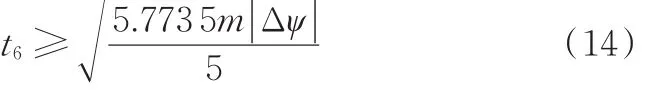
Z向位置调整时间t6取最小整数值。

5 舱段调姿仿真验证

通过UG8.0软件建立舱段的仿真模型，并对移动卡环调姿机构和调姿工作台进行简化，建立仿真模型（图7）。将建立的模型导入ADAMS，利用ADAMS修改对接舱段模型各部件属性，定义O1、O2、O3三个关键点，其中,O1点为舱段对接面圆心，O2点为定位销孔圆心，O3为舱段轴线上一点，其中，l1=905 mm，l2=330 mm，l3=287.58 mm。

图7 仿真模型Fig.7 Simulation model

舱段初始位姿为

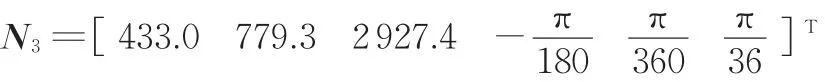
调姿标位姿为

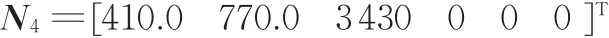
根据调姿算法要求，在模型上添加相应的运动副、载荷及驱动。由式（8)可得偏转调姿的偏转调姿时间t1=4 s、俯仰调姿时间t2=3 s、横滚调姿时间t3=4 s，由式（11)可得Y方向位置调整时间t4=7 s、X方向位置调整时间t5=7 s，由式（14)可得Z向对接时间t6=17 s。

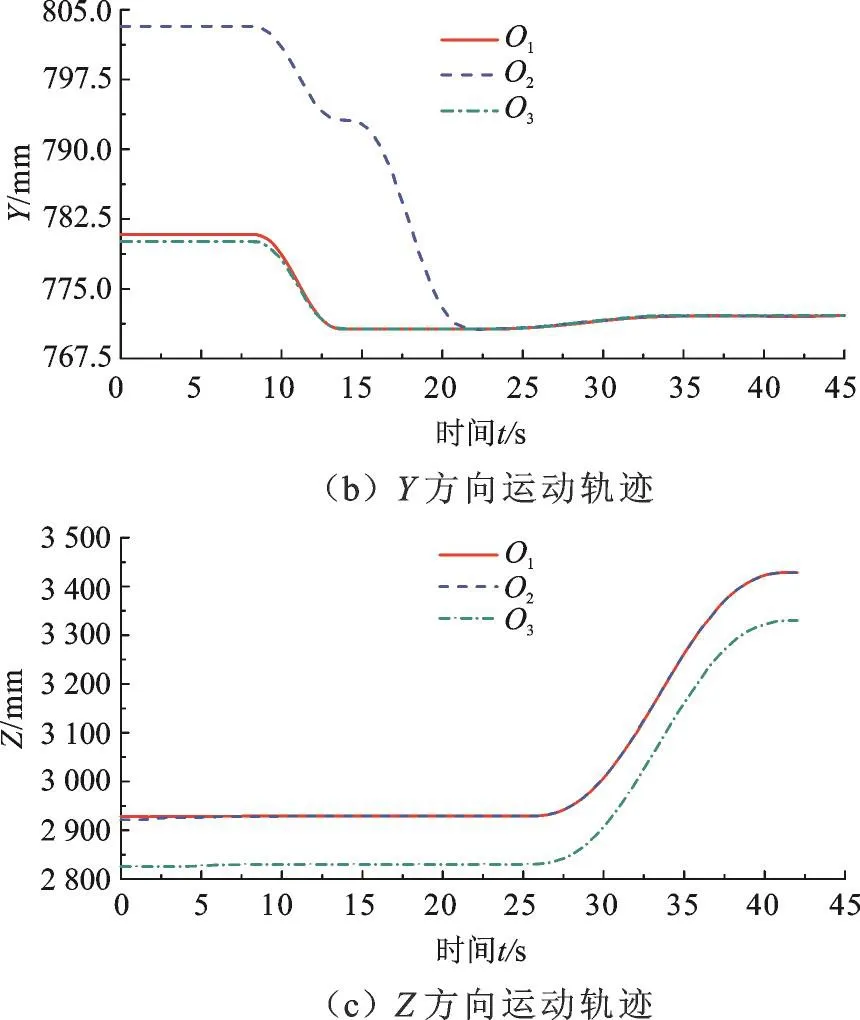
图8 关键点运动轨迹Fig.8 Key point motion trajectory

由图8a、图8b可以看出，运动仿真结束后，O1点和O3点的X、Y坐标值相同，说明对接舱段参考坐标系的Z1轴与全局坐标系的Z轴平行，在图8b中，O2点的Y坐标值在仿真结束后，与O1点和O3点的Y坐标值相同，说明调姿结束后，对接舱段参考坐标系的X1轴与全局坐标系的X轴平行，参考坐标系的X1轴、Z1轴分别与全局坐标系的X轴、Z轴平行，说明舱段达到了目标姿态；由图8读出调姿结束后O1点的X、Y、Z坐标分别为409.96 mm、769.92 mm、3 430 mm，与目标坐标值在X轴方向上偏差为-0.04 mm，在Y轴方向上偏差为-0.08 mm，误差在允许范围内，O1点位置达到了目标位置。

偏转调姿过程中，对接舱段轴线（O1O3）绕Y轴旋转的角速度、角加速度曲线见图9，角加速度的绝对值最大值为0.36 °/s2，满足式（8）。

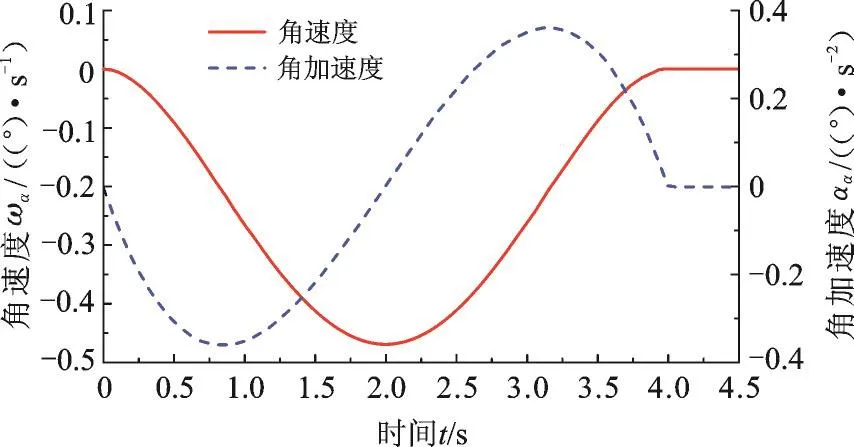
图9 对接舱段轴线绕Y轴运动的角速度及角加速度Fig.9 The movement angular velocity and acceleration of the axis of docking cabin aroundYaxis

俯仰调姿过程中，对接舱段轴线绕X轴旋转的角速度、角加速度曲线见图10，角加速度的绝对值最大值为0.32 °/s2，满足式（8)。

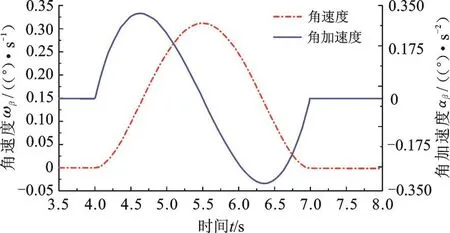
图10 对接舱段轴线绕X轴运动的角速度及角加速度Fig.10 The movement angular velocity and acceleration of the axis of docking cabin aroundXaxis

横滚调姿过程中，对接舱段绕自身轴线旋转的角速度、角加速度曲线见图11，角加速度最大绝对值为1.8 °/s2，满足式（8)。

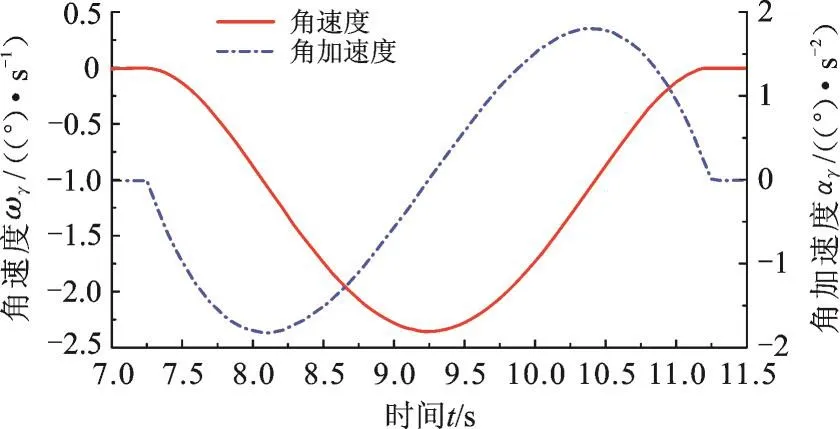
图11 对接舱段轴线绕Z轴运动的角速度及角加速度Fig.11 The movement angular velocity and acceleration of the axis of docking cabin around Z axis

在对舱段进行位置调整时，3个方向的运动时间约束公式相同，且在Z轴方向上的调整量较大，即舱段在Z轴方向上的运动速度与加速度较大，如图12所示，O1点在Z轴方向运动时最大加速度为10 mm/s2，满足式（9)。

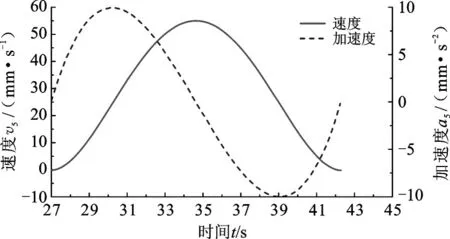
图12 O1点在Z轴方向上的运动的速度及加速度Fig.12 The movement velocity and acceleration ofO1 in Z-axis direction

6 结论

（1）针对一类圆柱形舱段对接过程进行研究，提出了两点定位调姿法，通过在舱段周围布设关键点，在装配空间内建立全局坐标系，在对接面圆心处建立参考坐标系，建立了舱段调姿数学模型，经仿真验证，两点定位调姿法具有较高的精度。

（2）采用五次多项式轨迹对舱段进行调姿轨迹规划，经仿真验证，舱段在姿态调整和位置调整时调姿轨迹平滑无跳动，即舱段运行平稳，加速度或角加速度满足约束要求，且调姿时间合理。

（3）两点定位调姿法将舱段姿态调整过程分为偏转调姿、俯仰调姿与横滚调姿，简化了调姿算法，在对舱段进行姿态调整时所绕坐标轴为全局坐标轴，串联调姿机构即可满足调姿算法要求，避免了多轴协调控制，降低了控制难度。

［1］ 郭志敏，蒋君侠，柯映林.基于POGO柱三点支撑的飞机大部件调姿方法［J］.航空学报,2009,30（7）:1319⁃1324.GUO Zhimin，JIANG Junxia，KE Yinglin.Posture Alignment for Large Aircraft Parts Based on Three POGO Sticks Distributed Support［J］.Acta Aero⁃nautica et Astronautica Sinica,2009,30（7）:1319 ⁃1324.

［2］ PAULOS J，ECKENSTEIN N，TOSUN T，et al.Automated Self⁃assembly of Large Maritime Struc⁃tures by a Team of Robotic Boats［J］.IEEE Trans⁃actionsonAutomationScience& Engineering，2015，12（3）:958⁃968.

［3］ 谢志江，赵萌萌.机器视觉辅助的4⁃PPR并联机构工作空间分析［J］.机械设计,2013,30（3）:40⁃43.XIE Zhijiang，ZHAO Mengmeng.Workspace Analy⁃sis for Vision⁃aided 4⁃PPR Parallel Mechanism［J］.Journal of Machine Design,2013,30（3）:40⁃43.

［4］ 杨冬，李铁军，刘今越，等.3⁃UPS/S并联平台结构设计与运动学分析［J］.机械设计,2014,31（3）:47⁃50.YANG Dong，LI Tiejun，LIU Jinyue，et al.Design and Kinematic Analysis of 3⁃UPS/S Parallel Mech⁃anism［J］.Journal of Machine Design，2014,31（3）：47⁃50.

［5］ LI Yuan，YU Jianfeng，ZHANG Jie，et al.A Posture Evaluation Method for Aircraft Wing Based on a Simple Measurement System［J］.Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，2013,227（4）:627⁃630.

［6］ 易旺民，段碧文，高峰，等.大型舱段装配中的水平对接技术［J］.计算机集成制造系统,2015,21（9）:2354⁃2360.YI Wangmin，DUAN Biwen，GAO Feng，et al.Level Docking Technology in Large Cabin Assembly［J］.Computer Integrated Manufacturing Systems，2015，21（9）：2354⁃2360.

［7］ 蒋君侠，范子春，郭志敏，等.适用于三段大部件对接的柔性装配平台设计与优化［J］.浙江大学学报（工学版）,2010,44（9）:1798⁃1804.JIANG Junxia，FAN Zichun，GUO Zhimin,et al.De⁃sign and Optimization of Flexible Assembly Plat⁃form Used for Three Sections Joint［J］.Journal of Zhejiang University（Engineering Science）,2010,44（9）:1798⁃1804.

［8］ GUO Zhimin，JIANG Junxia，KE Yinglin.Stiffness of Postural Alignment System Based on 3⁃axis Ac⁃tuators for Large Aircraft Components［J］.Chinese Journal of Mechanical Engineering，2010,23（4）:524⁃531.

［9］ 黄翔，陈磊，李泷杲，等.基于3⁃2⁃1随动式定位器的飞机部件位姿调整方法：201110401826.5［P］.2012⁃06⁃27.HUANG Xiang，CHEN Lei，LI Longgao，et al.Pose Adjustment Method of Aircraft Component Based on 3⁃2⁃1 Follower Positioner:201110401826.5［P］.2012⁃06⁃27.

［10］ 张斌，方强，柯映林.大型刚体调姿系统最优时间轨迹规划［J］.机械工程学报,2008,44（8）:248⁃252.ZHANG Bin，FANG Qiang，KE Yinglin.Optimal Time Trajectory Planning Method for a Kind of Posture Aligning System of Large Rigid Bodies［J］.Chinese Journal of Mechanical Engineering,2008,44（8）:248⁃252.

［11］ 刘继红，庞英仲，邹成.基于关键特征的飞机大部件对接位姿调整技术［J］.计算机集成制造系统,2013,19（5）:1009⁃1014.LIU Jihong，PANG Yingzhong，ZOU Cheng.Ad⁃justing Position⁃orientation of Large Components Based on Key Features［J］.Computer Integrated Manufacturing Systems，2013,19（5）:1009⁃1014.

［12］ 朱永国，黄翔，李泷杲,等.飞机装配高精度测量控制网精度分析与构建准则［J］.中国机械工程，2014,25（20）:2699⁃2704.ZHU Yongguo，HUANG Xiang，LI Longgao，et al.Precision Analysis and Layout Rules of Surveying Control Network for Aircraft Assembly［J］.China Mechanical Engineering，2014,25（20）:2699⁃2704.

［13］ 王少锋，张进华，刘志刚，等.大型飞机机身壁板装配位姿调整系统的运动规划［J］.西安交通大学学报，2011,45（3）:102⁃106.WANG Shaofeng，ZHANG Jinhua，LIU Zhigang，et al.Motion Planning for Alignment Machine Tool Oriented Fuselage Panel［J］.Journal of Xi’an Jiao⁃tong University，2011,45（3）:102⁃106.

［14］ 崔学良，韩先国，陈五一.大尺寸弱刚性构件对接装配系统轨迹规划［J］.计算机集成制造系统,2011,17（5）:908⁃914.CUI Xueliang，HAN Xianguo，CHEN Wuyi.Tra⁃jectory Planning for a Large Scale Weak Rigid Component Docking Assembling System［J］.Com⁃puter Integrated Manufacturing Systems,2011,17（5）:908⁃914.

［15］ 应征，黄浦缙，王青，等.飞机大部件调姿机构柔性多体动力学建模与仿真［J］.计算机集成制造系统,2012,18（11）:2470⁃2475.YING Zheng，HUANG Pujin，WANG Qing，et al.Modeling and Simulation of Flexible Multi⁃body Dynamics for Large Aircraft Components Align⁃ment Mechanism［J］.Computer Integrated Manu⁃facturing Systems,2012,18（11）:2470⁃2475.

［16］ 屈稳太，应蓓华，董凤莲.大刚体姿态计算及多轴同步协调控制技术［J］.中国机械工程,2014,25（22）:3050⁃3055.QU Wentai，YING Beihua，DONG Fenglian.Calcu⁃lation of Large Rigid Body Pose and Multi⁃axis Synchronous Coordinating Control［J］.China Me⁃chanical Engineering，2014,25（22）:3050⁃3055.

［17］ 张斌，姚宝国，柯映林.基于鞍点规划理论的机翼水平位姿评估方法［J］.浙江大学学报（工学版）,2009,43（10）:1761⁃1765.ZHANG Bin，YAO Baoguo，KE Yinglin.Saddle Point Programming Based Level⁃ posture Evalua⁃tion Method for Aircraft Wings［J］.Journal of Zheji⁃ang University（Engineering Science）,2009,43（10）:1761⁃1765.

［18］ CALUDE C S，CALUDE E，QUEEN M S.The Complexity of Euler’s Integer Partition Theorem［J］.Theoretical Computer Science，2012,454：72⁃80.

［19］ 高超.导弹柔性装配系统关键技术研究［D］.哈尔滨：哈尔滨工业大学,2014.GAO Chao.Research on Key Technologies of Mis⁃sile Flexible Assembly System［D］.Harbin：Harbin Institute of Technology,2014.

［20］ 郭嗣琮，刘秀华，韩建.模糊值函数的极值问题［J］.系统工程理论与实践，2014（3）:738⁃745.GUO Sicong，LIU Xiuhua，HAN Jian.Extremal Problem of Fuzzy⁃valued Function［J］.Systems En⁃gineering Theory&Practice，2014（3）:738⁃745.*