镁合金正挤压−弯曲剪切复合连续变形工艺及挤压力计算

胡忠举，刘雁峰，卢立伟, , ，伍贤鹏，刘楚明



镁合金正挤压−弯曲剪切复合连续变形工艺及挤压力计算

胡忠举1，刘雁峰1，卢立伟1, 2, 3，伍贤鹏2，刘楚明3

(1. 湖南科技大学 难加工材料高效精密加工湖南省重点实验室，湘潭 411201；2. 湖南科技大学 高温耐磨材料及制备技术 湖南省国防科技重点实验室，湘潭 411201；3. 中南大学 材料科学与工程学院，长沙 410083)

结合传统挤压与弯曲剪切变形的特点提出一种棒−板正挤压−弯曲剪切复合连续变形新工艺，该工艺既可显著细化晶粒又可以弱化织构，极大地改善镁合金的综合力学性能。通过分析该复合变形方式的特点，建立了总挤压力数学模型，对正挤压−弯曲剪切复合成形所需的挤压力进行了系统、完整、准确的表征。根据各分区的变形特点，把实际的正挤压模型类比成等效面积的圆棒挤压模型，并引入形状复杂系数，利用上界法得出各分区的挤压力解析表达式，基于有限元数值模拟对形状复杂系数进行分析求解。最后通过与实验结果的比较得出该模型计算的结果与实际值的误差在5%的范围内，满足工程计算要求。

镁合金；正挤压−弯曲剪切复合变形；显微组织；力学性能；形状复杂系数；挤压力

随着航空、航天、国防武器装备、交通运输工具等行业的高速发展，当今社会对优良综合性能的材料特别是比强度和比刚度高的轻质镁合金材料需求持续迅猛增长，研究与制备具有高性能的镁合金材料一直是各国材料领域的学者们研究的热点[1−3]。在这样的实际背景下，大塑性变形技术(Severe plastic deformation, SPD)也就被人提出并慢慢得到了一定的发展，SPD技术既能细化晶粒组织，又可以对织构弱化进行控制，在晶粒细化与织构控制协同作用下能获得具有高性能的产品，是一种引起多数学者深入研究且具有广泛影响力的成形技术[4−5]。近些年逐渐发展起来的SPD技术主要有循环挤压(CEC)[6]、涡流挤压(VE)[7]、高压扭转挤压(HPT)[8−9]、循环向前向后挤压(CFBE)[10−11]、等通道挤压(ECAP)等[12]。对于这些大塑性变形技术，不少研究工作者针对各种工艺参数及模具的结构参数对试样微观组织以及各力学性能的影响做了大量的研究。LIN等[13]研究了GW120K镁合金通过CEC后晶粒细化与织构弱化对试样的强度与延展性的影响。SHAHBAZ等[14]通过实验与有限元模拟研究了VE的塑性变形行为，与传统正挤压(CE)对比发现，VE后的试样晶粒组织细小、应变值大、变形更剧烈，所需的挤压力也相对较高。LEE等[15]研究了镁铝合金通过HPT后晶粒细化对显微组织与力学性能的影响。目前，研究工作者对ECAP的研究主要以工艺参数对力学性能的影响、金属的流动规律、晶粒细化机理、超细晶的制备为主要研究方向，而对工艺的可行性研究还不够全面[16]。EBRAHIMI等[17]研究了等通道正挤压对6082铝合金试样组织与性能的影响，该成形技术的优点是在挤压力较小的情况下样品可以得到较高且分布较均匀的等效应变。胡红军[18]等通过实验测试与有限元数值模拟研究了ECAP模具外角变化与倒角有无对挤压力的影响。RAHIMI等[19]在纯剪切挤压中研究了不同的模具结构参数与摩擦因数对挤压力的影响。PRIEL等[20]建立了Mg/Al复合坯在复合挤压中的挤压力预测模型，并通过试验验证了该模型的可靠性。晶粒的细化与织构弱化的控制可以提高材料的综合性能，是改良材料强韧性的关键所在。尽管SPD可以通过多种方法来显著细化材料晶粒以及对织构弱化进行控制，但是多数SPD技术属于多道次非连续成形，具有生产效率低、生产成本高、工艺复杂等特点，仅局限于试验研究，很难投入到大批量商业化生产当中。

本文作者提出了一种集正挤压与多次弯曲剪切变形于一体的棒−板正挤压−弯曲剪切复合连续变形新工艺，能显著地细化晶粒以及对织构弱化的控制，具有效率高、成本低、工艺简单、一道次成形等特点。本文作者采用上界法和数值模拟相结合建立了新型塑性成形工艺的挤压力数学模型，并通过实验验证了该数学模型与实际情况的吻合程度，为该成形工艺的可行性研究提供了理论参考。

1 模具结构及变形特点

正挤压−弯曲剪切复合连续变形模具的结构如图1(a)所示。包括凸模和凹模(分左右半模)，所述的凹模型腔由挤压通道和凸模通道两部分组成。挤压通道可分为正挤压区和弯曲剪切区，正挤压区见图1(a)中I所标识的区域，弯曲剪切区见图1(b)所示，起强剪切作用的结构见图1(b)中Ⅱ、Ⅲ、Ⅳ、Ⅴ所示。

图1 正挤压−弯曲剪切复合成形模具示意图、模具图及局部放大图

图2所示为金属变形区域分布示意图。图2可知模具的型腔结构参数，包括正挤压区锥角，挤压通道弯曲角与，挤压通道弯曲过渡半径1与2，过渡直线段1、2、3、4、5，等截面弯曲剪切挤压通道厚度、宽度，凸模通道直径0。

当挤压机带动凸模开始往下移动时，镁合金锭坯充盈凹模挤压筒并通过刚性流动区；接着进入正挤压变形区，发生剧烈的塑性变形；通过正挤压变形区后，锭坯由棒材完全成形为板材；随着挤压的进行，板材会依次通过图2中3、4、5、6所示的4个弯曲剪切区，受到4次强剪切变形后最终成为所需的试样。由图2还可知，正挤压区左右成平面对称，弯曲剪切区以图2中点成中心对称，这种对称结构的设计使得板材的两侧变形程度以及流速均匀，为高质量的板材生产提供了基础。

图2 金属变形区域分布示意图

2 挤压力计算

通过对正挤压−弯曲剪切复合连续变形模具型腔以及金属流动特点的分析，可把总挤压力的计算初步分为正挤压区和弯曲剪切区两个大块分别进行推导。

2.1 正挤压区挤压力计算

锭坯通过正挤压区时由棒材成形为板材会发生剧烈的塑性变形，变形过程十分复杂，在数学上求得该区的挤压力相当困难。但可以把实际的棒−板挤压模型类比成等效面积的棒−棒挤压模型[21]，如图3所示，同时引入形状复杂系数1(，)。

实际的棒−板挤压变形的挤压力记为1′，等效面积的棒−棒挤压变形的挤压力记为1*，考虑到形状复杂系数1(，)，1′与1*对应关系为

图4 等效面积的棒−棒挤压速度场模型

采用上界法[22]计算得出等效面积的棒−棒挤压总变形功率*为

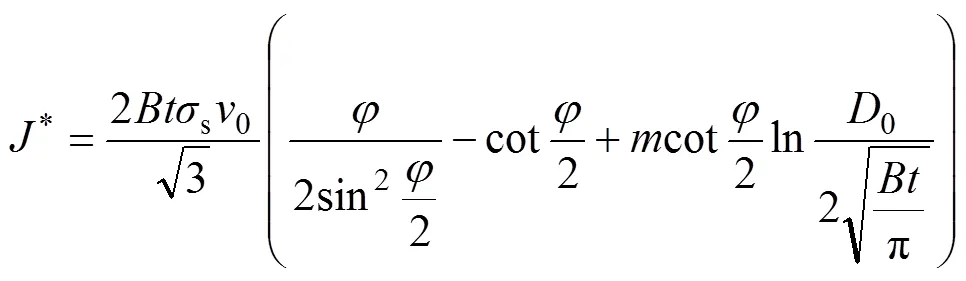
式中：s为AZ31镁合金的屈服强度；为摩擦因数。

总变形力1*为

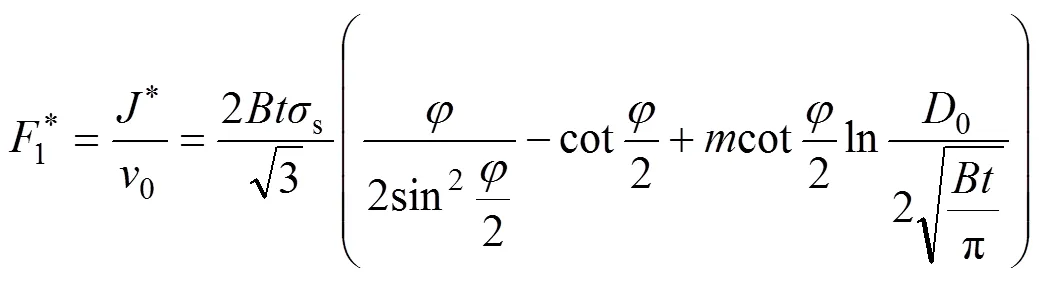
式中：0为锭坯与挤压筒壁的接触面积；为锭坯长度；6为挤压筒内锭坯进入正挤压锥角区的长度。

则棒−板挤压总挤压力1为

2.2 弯曲剪切区的挤压力计算

由图2可知，弯曲剪切区可细分为4个强剪切区，弯曲剪切区Ⅰ的流动模型与速端图如图5所示，在图5(a) 1区中，11弧面和11弧面以及弧面和弧面均为粗糙面，且分别连为一体作为刚性支撑面，锭坯1面是随1面向下运动而运动的自由面，1面为速度不连续面，变形区由两个扇环刚性块11和11组成，最终可确定变形区的速端图(图中t为切向速度，为二分之一挤压通道的弯曲角)。

图5 流动模型与速端图

运用上界法，根据运动许可速度场确定的总变形功率1*为

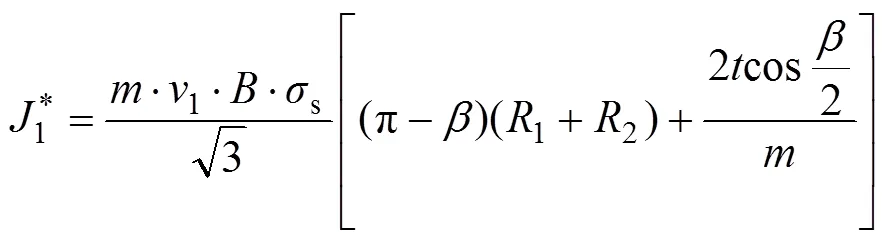
弯曲剪切Ⅰ区单位面积上的上限载荷*和变形力1*分别为

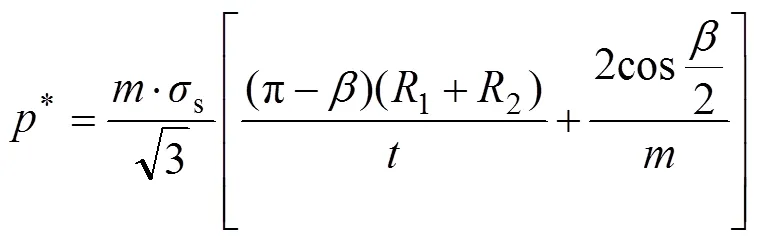
弯曲剪切区2、3、4的变形力2*、3*、4*分 别为

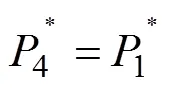
弯曲剪切区总接触摩擦力为

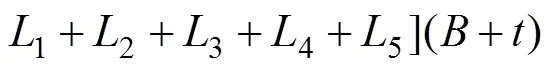
因此，弯曲剪切区总挤压力2为

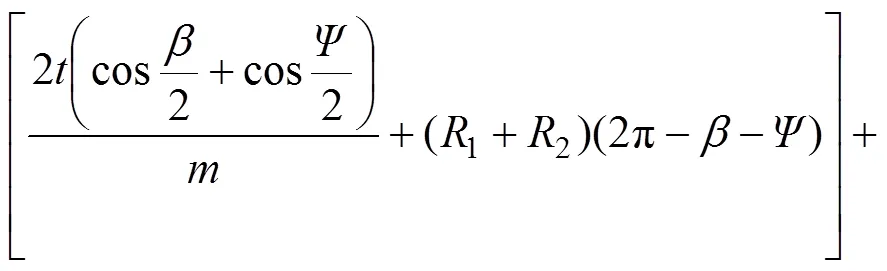
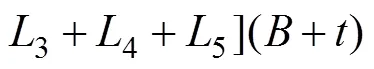
则正挤压−弯曲剪切变形模型的总挤压力数学模型为

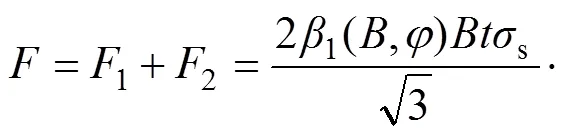
3 形状复杂系数β1(B，φ)的确定

在锭坯温度为400 ℃、板厚为3 mm时，通过改变锥角，运用Deform-3D对正挤压−弯曲剪切复合连续变形工艺进行数值模拟，在软件中定义各参数：0、、、、、1、2、1、2、3、4、5、、、0，得到形状复杂系数1(25，)与的关系如图6所示。

图6 形状复杂系数β1(25，φ)与锥角φ的关系

采用多项式对图6中形状复杂系数1(25，)与的关系进行曲线拟合，多项式为

式中：0=−0.42249；1=0.03556；2=−0.000396；3=0.0000016。

采用3次多项式拟合，判断系数2=0.99147，通过拟合后形状复杂系数表达式为

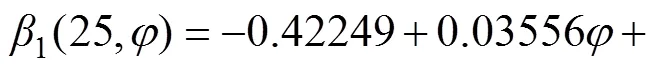
为了研究形状复杂系数1(，)与板宽的关系，通过改变板宽，运用Deform-3D对其进行数值模拟，其他参数设置与上述一致。得到形状复杂系数1(,60)与的关系如图7所示。

采用多项式对图7中形状复杂系数1(，60)与的关系进行曲线拟合，多项式为

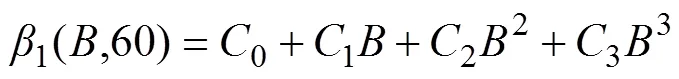
式中：0=4.09303；1=−0.22204；2=0.00198；3=0.0000563。

采用3次多项式拟合，判断系数2=0.98856，通过拟合后形状复杂系数表达式为

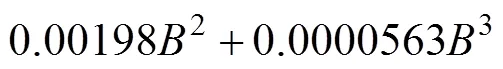
将式(18)曲线作为截面曲线，以式(16)曲线作为引导线构建曲面，得到形状复杂系数1(，)表达式为

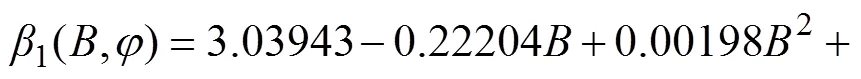
图8所示为形状复杂系数1(，)的三维曲面图。

图7 形状复杂系数β1(B，60)与板宽B的关系

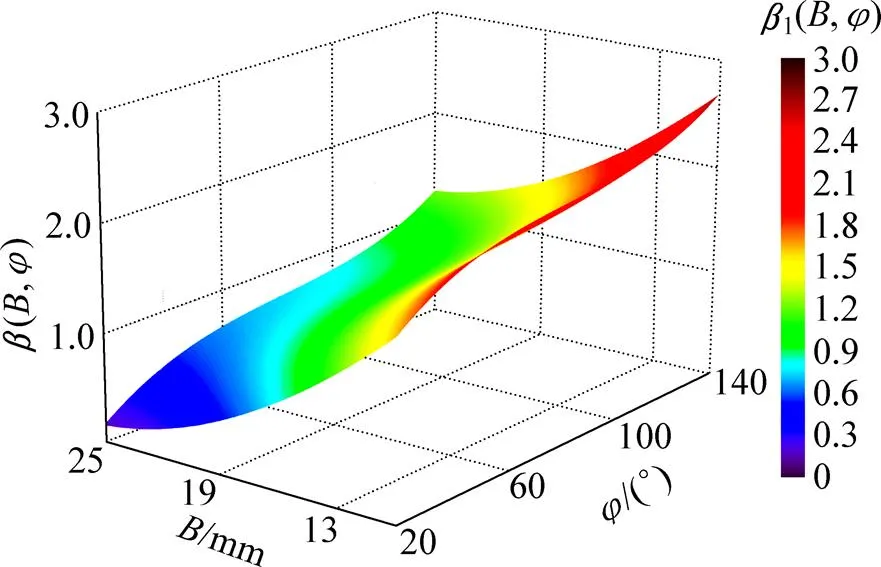
图8 形状复杂系数β1(B，φ)三维曲面图

AZ31镁合金锭坯温度为400 ℃、板厚为3 mm时，正挤压−弯曲剪切变形的总挤压力为

4 实验验证

图9所示为模具实物，结构参数值：=25 mm、=60°、0=26 mm、=3 mm、=140°、=100°、1=6 mm、2=3 mm、1=3 mm、2=3=4=0.68 mm、5= 4 mm。实验选用的工艺参数为：=0.3、=400 ℃，0=2 mm/s，镁合金棒锭坯尺寸：×=25 mm×25 mm，采用100 t立式锻压机对AZ31镁合金锭坯进行正挤压−弯曲剪切复合连续变形实验。由检测与分析得出AZ31镁合金在400 ℃以及对应的应变速率下s=35 MPa，最终经实验测试、数值模拟与数学模型计算得出的总挤压力结果分别为285、269.3和277.6 kN。实验测试值与数学模型计算值有一定误差。主要原因可能是由于在实际挤压过程中，模具温度比毛坯温度低，锭坯与模具之间发生热传导，锭坯温度有所下降，导致实际挤压力比模型计算出的挤压力高，该误差为2.6%，在可接受的范围内，可以满足工程计算的要求。

图9 正挤压−弯曲剪切复合成形模具实物图

为了研究正挤压−弯曲剪切复合连续变形工艺对AZ31镁合金综合性能的影响，采用图9所示模具在不同的工艺条件下进行了挤压实验，并对所获取的挤压样品进行了相关检测与分析。由金相检测结果显示，正挤压−弯曲剪切复合连续变形工艺可显著改善镁合金的显微组织，经一道次成形后平均晶粒尺寸由原始铸态的240 μm可显著均匀细化至0.5 μm，如图10(a)和(b)所示。

该复合工艺不仅可以对镁合金晶粒进行显著细化，而且能极大地提高了镁合金的综合力学性能，是一种极具发展潜力和应用前景的加工方法。当挤压温度为370℃时，经正挤压−弯曲剪切复合成形后，AZ31镁合金板材的抗拉强度高达307 MPa，屈服强度高达232 MPa(见图11中的曲线1)。当挤压温度为290℃时，获得的AZ31镁合金板材的室温断裂伸长率高达28.6%(见图11中曲线2)。

图10 AZ31镁合金挤压变形前后的微观组织

图11 正挤压−弯曲剪切复合成形AZ31镁板应力−应变曲线

5 结论

1) 棒−板正挤压−弯曲剪切复合连续变形工艺既可显著细化晶粒又可以弱化织构，极大地改善了镁合金的综合力学性能，具有可连续生产、效率高、成本低、工艺简单、一道次成形等特点。

2) 通过上界法与数值模拟相结合得出了形状复杂系数的表达式，并建立了正挤压−弯曲剪切复合成形技术的总挤压力数学模型。

3) AZ31镁合金在实际挤压过程中的挤压力在285 kN左右，通过总挤压力数学模型计算出的挤压力为277.6 kN，相比误差为2.6%，可以满足工程计算的要求。

4) 挤压力的推导与计算可为模具的设计提供理论基础，为实际生产过程中挤压机设备的选择以及挤压加工可行性分析提供了有利依据。

[1] 刘 筱, 朱必武, 李落星, 唐昌平. 挤压态AZ31镁合金热变形过程中的孪生和织构演变[J]. 中国有色金属学报, 2016, 26(2): 288−295. LIU Xiao, ZHU Bi-wu, LUY Luo-xing, TANG Chang-ping. Twinning and texture evolution in extruded AZ31 magnesium alloy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(2): 288−295.

[2] 唐伟琴, 李大永, 彭颖红. AZ31镁合金板材冲压成形制耳的晶体塑性模拟[J]. 中国有色金属学报, 2014, 24(8): 1933−1940. TANG Wei-qin, LI Da-yong, PENG Ying-hong. Crystal plasticity simulation on earing during deep drawing of AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(8): 1933−1940.

[3] 吴章斌, 桂良进, 范子杰. AZ31B镁合金挤压材料的力学性能与本构分析[J]. 中国有色金属学报, 2015, 25(2): 293−300. WU Zhang-bin, GUI Liang-jin, FAN Zi-jie. Mechanical properties and constitutive analysis of extruded AZ31B magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 293−300.

[4] 何运斌, 潘清林, 刘晓艳, 李文斌. ECAP法制备细晶ZK60镁合金的微观组织与力学性能[J]. 材料工程, 2011(6): 32−38. HE Yun-bin, PAN Qing-lin, LIU Xiao-yan, LI Wen-bin. Microstructure and mechanical properties of ZK60 magnesium alloy produced by equal channel angular pressing[J]. Journal of Materials Engineering, 2011(6): 32−38.

[5] 刘满平, 王俊, 蒋婷慧, 吴振杰, 谢学锋. 高压扭转大塑性变形Al-Mg铝合金中的层错和形变孪晶[J]. 中国有色金属学报, 2014, 24(6): 1383−1392. LIU Man-ping, WANG JUN, JIANG Ting-hui, WU Zhen-jie, XIE Xue-feng. Stacking faults and deformation twins in Al-Mg alloys subjected to high pressure torsion[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1383−1392.

[6] CHEN Y J, WANG Q D, ROVEN H J, LIU M P. Network-shaped fine-grained microstructure and high ductility of magnesium alloy fabricated by cyclic extrusion compression[J]. Scripta Materialia, 2008, 58(4): 311−314.

[7] SHAHBAZ M, PARDIS N, EBRAHIMI R, TALEBANPOUR B. A novel single pass severe plastic deformation technique: Vortex extrusion[J]. Materials Science and Engineering A, 2011, 530(1): 469−472.

[8] MENG F Q, ROSALIE J M, SINGH A, SOMEKAWA H, TSUCHIYA K. Ultrafine grain formation in Mg-Zn alloy by in situ precipitation during high-pressure torsion[J]. Scripta Materialia, 2014, 78: 57−60.

[9] TORBATI-SARRAF S A, LANGDON T G. Properties of a ZK60 magnesium alloy processed by high-pressure torsion[J]. Journal of Alloys and Compounds, 2014, 613: 357−363.

[10] ALIHOSSEINI H, ZAEEM M A, DEHGHANI K. Producing ultrafine-grained aluminum rods by cyclic forward-backward extrusion: Study the microstructures and mechanical properties[J]. Materials Letters, 2012, 74(5): 147−150.

[11] ALIHOSSEINI H, ZAEEM M A, DEHGHANI K. A cyclic forward-backward extrusion process as a novel severe plastic deformation for production of ultrafine grains materials[J]. Materials Letters, 2012, 68(2): 204−208.

[12] 卢立伟, 赵 俊, 刘龙飞, 陈志钢, 刘天模. 镁合金大塑性变形的研究进展[J]. 材料热处理学报, 2014, 35(s1): 1−7. LU Li-wei, ZHAO Jun, LIU Long-fei, CHEN Zhi-gang, LIU Tian-mu. Research achievements of severe plastic deformation on magnesium alloys[J]. Transactions of Materials and Heat Treatment, 2014, 35(s1): 1−7.

[13] LIN J, WANG X, REN W, YANG X, WANG Q. Enhanced strength and ductility due to microstructure refinement and texture weakening of the GW102K alloy by cyclic extrusion compression[J]. Journal of Materials Science and Technology, 2016, 32(8): 783−789.

[14] SHAHBAZ M, PARDIS N, KIM J G, EBRAHIMI R, KIM H S. Experimental and finite element analyses of plastic deformation behavior in vortex extrusion[J]. Materials Science and Engineering A, 2016, 674: 472−479.

[15] LEE H J, HAN J K, JANAKIRAMAN S, AHN B, KAWASAKI M. Significance of grain refinement on microstructure and mechanical properties of an Al-3%Mg alloy processed by high-pressure torsion[J]. Journal of Alloys and Compounds, 2016, 686: 998−1007.

[16] 赵鸿金, 胡玉军, 彭 凯, 李涛涛. 方形等通道角挤压力计算与分析[J]. 塑性工程学报, 2015(6): 15−20. ZHAO Hong-jin, HU Yu-jun, PENG Kai, LI Tao-tao. Calculation and analysis of extrusion force in square equal channel angular pressing[J]. Journal of Plasticity Engineering, 2015(6): 15−20.

[17] EBRAHIMI M, GHOLIPOUR H, DIAVANROODI F. A study on the capability of equal channel forward extrusion process[J]. Materials Science and Engineering A, 2016, 650: 1−7.

[18] HU Hong-jun, ZHANG Ding-fei, PAN Fu-sheng. Die structure optimization of equal channel angular extrusion for AZ31 magnesium alloy based on finite element method[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(2): 259−266.

[19] RAHIMI F, EIVANI A R, KIANI M. Effect of die design parameters on the deformation behavior in pure shear extrusion[J]. Materials Design, 2015, 83: 144−153.

[20] PRIEL E, UNGARISH Z, NAVI N U. Co-extrusion of a Mg/Al composite billet: A computational study validated by experiments[J]. Journal of Materials Processing Technology, 2016, 236: 103−113.

[21] 黄克坚, 包忠诩, 黄志超, 朱永光. 宽展挤压变形及挤压力的计算[J]. 塑性工程学报, 2004, 11(5): 41−45. HUANG Ke-jian, BAO Zhong-xu, HUANG Zhi-chao, ZHU Yong-guang. The analysis of spread extrusion forming law[J]. Journal of Plasticity Engineering, 2004, 11(5): 41−45.

[22] 王振范, 刘相华. 能量理论及其在金属塑性成形中的应用[M]. 北京: 科学出版社, 2009. WANG Zhen-fan, LIU Xiang-hua. Energy princple and it’s application in metal forming[M]. Beijing: Science Press, 2009.

Continuous deformation technology and extrusion load calculation of Mg alloys fabricated by direct extrusion and bending shear deformation

HU Zhong-ju1, LIU Yan-feng1, LU Li-wei1, 2, 3, WU Xian-peng2, LIU Chu-ming3

(1. Hunan Provincial Key Laboratory of High Efficiency and Precision Machining of Difficult-to-cut Material, Hunan University of Science and Technology, Xiangtan 411201, China; 2. Hunan Provincial Key Defense Laboratory of High Temperature Wear-resisting Materials and Preparation Technology, Hunan University of Science and Technology, Xiangtan 411201, China; 3. School of Materials Science and Engineering, Central South University, Changsha 410083, China)

Combining with the features of traditional extrusion and bending shear deformation, a new technology of rod-plate direct extrusion and bending shear compound deformation was proposed, which can not only significantly refine the grain size, but also weaken the texture, thus improve the mechanical properties of Mg alloys greatly. Based on the analysis of the compound deformation features, the mathematical model of the total extrusion load was established, The extrusion force required for direct extrusion bending shear compound deformation is systematically, completely and accurately characterized. According to the deformation features of each zone, the actual direct extrusion model can be analogized to the equivalent area of extruded bar model, and a complex shape coefficient is introduced. The upper bounding method is used to get analytical expression of the extrusion force of each zone. The complex coefficient of shape is analyzed and solved based on the finite element numerical simulation. Finally, the research result shows that the error range between calculated value from the mathematical model and the actual value is below 5%, which can satisfy the engineering calculation requirement.

Mg alloys; direct extrusion-bending shear compound deformation; microstructure; mechanical properties; complex shape coefficient; extrusion load

Project(51505143) supported by the National Natural Science Foundation of China; Project (2016T90759, 2014M562128) supported by Chinese Postdoctoral Science Foundation

2016-10-12;

2018-03-12

LIU Li-wei; Tel: +86-731-58290782；E-mail：cqulqyz@126.com

国家自然科学基金资助项目(51505143)；中国博士后科学基金资助项目(2016T90759，2014M562128)

2016-10-12；

2018-03-12

卢立伟，副教授，博士；电话：0731-58290782；E-mail：cqulqyz@126.com

10.19476/j.ysxb.1004.0609.2018.05.08

1004-0609(2018)-05-0923-08

TG376

A

(编辑 李艳红)