“生成性教学”理念下的高中数学教学设计

沈凌芳

（福建省漳州市第五中学，福建漳州 363000）

引 言

为了适应教育全面发展的需要，生成性学习模式得到越来越多教育专家的推崇。传统的教学模式，往往是教师在讲台上讲，学生在下面听（学、练），导致学生往往失去了应有的学习自主性，这也就预示着学生失去了对高中数学的学习兴趣。教师如果不能与时俱进，既会影响学生的自主学习能力，同时对国家相关素质教育教学方针也不能很好地及时贯彻实施。教师在高中数学教育教学过程中，适当运用生成性学习模式，一方面，可以培养学生科学探究的能力；另一方面，在学习的过程中，对思维锻炼、抽象概括等能力也有很大的帮助，同时还有利于学生其他能力的培养，如当下互联网信息时代追求的获取知识的能力、信息渠道拓展的能力、对收集到的信息进行处理归纳的能力、团队合作的能力，等等。

一、“生成性教学”概述

生成性学习，就是指我们在一些学科领域内，选取某个小问题、简单基础的问题作为整个复杂问题的突破口，通过探索尝试、交流互动、质疑等方式发现问题，引导学生发散思维，进而通过分析研讨，最后解决问题。这是一种通过表达与交流等形式为表象的探究学习活动；是学生获得知识、掌握基本思维方法的一种有效途径。它有助于学生在原有知识基础上，通过自主发现探究，使自身学习能力得到提高。因此教学实践活动中做好“生成性”的结合，不仅能够让学生原有的知识得到提高，还对学生高中数学思想和数学思维的形成起推波助澜的作用，更能促进学生个性化的成长及学习兴趣的提高[1]。

二、高中数学生成性教学设计策略分析

1.注重问题设计的开放性与弹性

“生成性教学”设计，首先需要明确的是课堂是教师和学生之间交流互动的平台，是将学生的“学”和教师的“教”创造性结合在一起的平台，是师生共同发展、体验的平台。为了能让师生更为充分地交流互动，能让课堂的“学”与“教”真正地融合，能让学生真正进步发展，“生成性教学”活动，教学中应该注重问题设计的开放性与弹性。但是问题设计的开放性与弹性，不代表可以简单随性，相反地，这更加考验我们教师的知识体系以及教学能力、综合能力，教师需要做足功课，充分考虑将教学的各个环节做出最为合理的安排。

例如，在学习“函数单调性”这一知识点时，我们可以进行如下的教学片段设计。

问题1：在图1所示函数图象中，我们如何形象化描述其变化趋势？（通过同学之间课堂讨论，得出结论：借助于“上升”“下降”等词汇来描述）

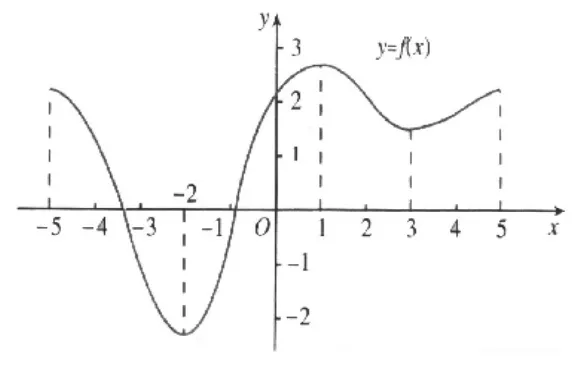
图1

问题2：这样的描述，能否准确地表示函数“单调递增 、单调递减”特性？

设计意图：通过设计问题1，我们可以浅入深出，循序渐进，将学生引向直观感觉或者经验之中，通过充分的课堂讨论，得出基本结论。之后再自然而然地过渡到问题2，引发学生思考，寻找问题答案，让我们的课堂变得生动有趣，使我们的学生，通过这种形式的探讨，参与到教学中，真正明白“函数单调性”，真正掌握如何采用数学语言，进行描述“函数单调性”。这样的教学设计，生动形象，引人深思，其具有一定的弹性和开放性，可以让学生通过深入地互动交流，真正明白仅仅用上升或者下降来表示函数的单调性，其本身就是不准确的，使学生深刻理解函数单调性的内涵，明白从严格意义上来讲，函数单调性只能用定义判定，明白数学知识与经验常识的区别，培养学生严谨的思维，避免掉入学习误区当中。借助于这两个递进式的问题，大大降低了学习的难度，加强了我们学生自主分析、思考的能力，强化了我们学生对相关数学概念的理解。

2.重点关注学生学习的全过程

“生成性教学”理念，关注的不应该仅仅是学习成绩，更多的是关注学生学习相关知识的全过程，尤其是在教学中，通过“生成性教学”，培养学生观察发现数学问题，进而针对这些问题建立相关数学模型，最后解决实际问题的能力。

例如，在学习“正弦定理”这一知识点时，我们可以进行如下的教学片段设计。

课程伊始，代入实际问题，引发学生思考：工人要对某学校活动教室进行维修，必须借助梯子到达屋顶，已知该活动教室高5m，墙体与水平地面垂直，梯子与地面夹角为40°，为了保证能爬上屋顶，梯子至少需要多长？

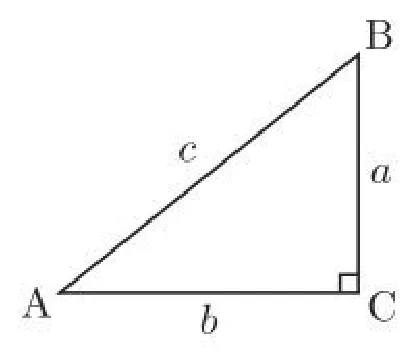
图2

以上问题比较简单，学生只要将实际问题抽象为数学模型即可，如图2所示。下面，教师就可以借助这个问题，发散学生思维，引出新知识点：如果原题中，墙体与水平地面夹角为90°，那么梯子长度至少需要多少米呢？这个问题是对问题1的升华，融入课堂所学的知识点，在学生原有知识点的基础上，做到环环相扣，知识点相互衔接，这时，我们就可以进入正题，讲正弦定理相关知识了。这样的教学处理不仅加深学生的印象，还打造了学生的知识体系，以点造面，更能提升学生的学习兴趣从而自主探索新知。教学中能较好地运用“生成性教学”，并始终关注学生学习的全过程，做到循序渐进由浅入深，学生们的思维能力与解决问题能力的培养是显而易见的。

3.注重培养学生思考问题的能力

学生只有养成发现问题、思考问题、探究问题、解决问题的习惯，才能为以后一步步提高综合素质打下良好基础。在教学过程当中，教师应当更加重视教学方法上的拓展和灵活性，创新教学内容与教学方式，引导我们的学生主动思考问题[2-3]。

例如，在学习“集合”这一知识点时，我们可以进行如下的教学片段设计。

刚刚教师已经举了有关集合的几个例子，现在我们大家来分组讨论下有关集合的例子。

学生 A：中国的所有直辖市。

教师：中国的所有直辖市，是不是对的啊？可不可以？学生：可以（一致）。

学生 B：中国的小河流。

教师：中国的小河流，是不是对的啊？可不可以？

学生：可以（有部分同学说不可以）。

教师：好，这个有不同意见啦。很好！那这个跟前面那个例子有什么区别呢？我们各个小组再讨论一下，给你们三分钟。

在这个教学设计中，给学生足够的时间与空间，让他们经过一番思考与讨论，他们对集合的概念将理解得比较到位。这样不仅锻炼了学生思考问题的能力，还达到提升课堂教学的效果，更让学生在学习中感受到成功的喜悦，提升了学生的学习兴趣。

结 语

“生成性教学”理念，旨在培养学生主动参与课堂学习，创设相关教学情境，引导学生学会主动分析，培养解决问题的能力。在高中数学的教育教学过程中，教师对学生的要求不能只是懂得知识就好，而是应该创造性地引入“生成性教学”理念。教学中将这个理念活用起来，让学生在掌握新知的基础上，同时还培养了学生发现问题、探索问题、解决问题的能力，这样有利于充分挖掘学生的学习潜力，培养学习的兴趣。

[参考文献]

[1] 邵洁.“生成性教学”理念指导下的高中数学教学设计策略[J].数学教学通讯,2017,(15):62-63.

[2] 徐小玲.基于生成性教学的高中数学课堂案例研究[D].广州大学,2017.

[3] 颜小情.基于动态生成的高中数学概念教学研究[D].福建师范大学,2014.