适应值共享小生境遗传算法实现与性能比较分析

赵 越，茹婷婷

(1.吉林建筑大学 计算机科学与工程学院，吉林 长春 130118; 2.吉林建筑大学 基础科学部，吉林 长春 130118)

小生境遗传算法是近年来兴起的一种进化计算技术.它以遗传算法为基础，将遗传操作中的每一代个体进一步划分为若干个类.对于每一个类，从中选择部分适应值较高的优秀个体组成一个群.算法在种群内部以及种群与种群之间完成遗传操作(包括选择、交叉、变异)，最终产生新一代群体.在算法的实现过程中，还可以采用分享机制、预选择机制和排挤机制等完成整个操作过程.由于小生境遗传算法能够更好的保持解空间群体的多样性，并且具有较好的全局搜索性能和收敛速度，故其在很多优化问题中有着越来越广泛的应用[1].下文对应用最多的基于适应值共享的小生境遗传算法进行分析和研究.

1 基于适应值共享小生境遗传算法的基本思想

基于适应值共享小生境遗传算法最早是由Goldberg和Richardson于1987年提出的，它是目前为止所有小生境技术中应用最多的方法之一[2].这种算法的基本思想是：将问题解空间的峰视为资源，该资源由峰周围的个体所共享.共享的方式是将个体的适应值除以资源周围的个体数，也就是说，个体被选择概率的调整是通过降低个体适应值来实现的.如果某个体距离其他个体较近，则适应值降低较多；如果某个体距离其他个体较远，则适应值降低较少.算法通过这样的机制使得排布稀疏的个体得到更多的机会繁衍，从而达到维持种群多样性的目的.适应值共享方法通常在选择操作前实施，以保证随后的选择操作能够根据共享后的适应值进行操作.

通常情况下，我们会对解空间的信息有一定了解.这部分信息主要包括峰的个数(k)或峰的半径(σ).我们也可根据事先提供信息量的不同，将适应值共享算法分为以下三类：仅使用k的算法，仅使用σ的算法及同时使用k和σ的算法.到目前为止，仅使用k的代表性算法有结合适应值共享的k均值聚类算法(由Yin等人提出)[3-4]；仅使用σ的算法主要包括标准适应值共享算法(由Goldberg等人提出)、清除算法(由Petrowski提出)和结合适应值共享的自适应k均值聚类算法(由Yin等人提出).同时使用k和σ的算法主要包括自适应小生境算法(由Goldberg等人提出)和动态小生境共享算法(由Miller等人提出).下面对常见适应值共享小生境遗传算法的实现机理进行研究.

2 常见基于适应值共享小生境遗传算法实现机理比较分析

2.1 标准适应值共享算法

该算法应用的前提条件是已知解空间中小生境半径，并要求峰半径都相同，算法的主要实现步骤如下.

step1 完成种群个体间共享函数s(dij) 的计算，公式如(1)所示:

(1)

(1)式中，dij表示群体中个体i和j间的距离，σ为预先给出峰的半径，α为函数的控制参数，一般取为1.通常而言，两个体间共享函数值越大，则两个体距离越近；

step2 完成种群中个体的共享值s(i)的计算，公式如(2)所示；

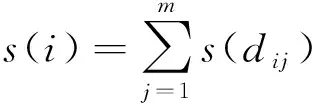
(2)

式(2)中，m为种群规模.通常来讲，个体的共享值越大，则该个体附近有越多的其他个体；

(3)

式(3)中，f(i)为共享前个体i的适应度；

step4 使用个体共享后的适应值完成遗传操作(即选择、交叉和变异)，完成新一代种群的生成.

应用标准适应值共享算法的前提是要预先知道峰的半径，假设峰的分布均匀且半径相同，这在实际问题中是很难满足的.尽管标准适应值共享算法的搜索效率和运算速度不很理想，但该算法的稳定性较好.故对于问题解空间结构未知的情形，可使用标准遗传算法求得进一步信息.

2.2 清除算法

标准适应值共享算法需要完成种群中所有个体间距离dij的计算，即种群中所有个体共享小生境内资源.若种群规模较大，则算法的效率将显著下降.为改进此算法，Petrowski于1996年提出了清除算法，该算法仅将有限资源提供给小生境内的若干最优个体.清除算法的实现步骤具体如下.

step1 将种群内的个体依照适应度降序排列；

step2 将第一个个体选作第一个小生境的中心；

step3 从第二个个体开始顺次执行以下步骤直到最末一个个体：

step3.1 若当前个体距离其他所有小生境中心都大于σ，则该个体成为新小生境的中心，并成为优胜者；

step3.2 若当前个体距离某小生境中心小于σ，且这个小生境中个体数量小于k，则将该个体放入该小生境，将该个体记为优胜者，并将小生境中个体数量加1；

step3.3 将其他个体标记为失败者；

step3.4 将全部失败者的适应度置零，并保持群体内所有优胜者的适应值不变；

step4 使用修改后个体的适应度值进行遗传操作(即选择、交叉和变异)，得到新一代种群.

如果将标准适应值共享算法中失败者的共享值看作无限大，而将优胜者的共享值看作1，则清除算法可以作为一种特殊的适应值共享算法.

2.3 结合适应值共享的自适应k均值聚类算法

结合适应值共享的自适应k均值聚类算法的主要思想如下.首先把群体按照随机的方式分为k组，分别与k个小生境相对应；由个体的原适应度除以个体的共享值s(i)得到个体的共享适应度.个体的共享值s(i)由式(4)给出.

(4)

式中，dic表示个体i与第c组中心之间的距离；nc表示第c组中个体数量；α通常取为1.一般说来，需预先给定参数dmax和dmin的值.dmax表示某个聚类中的个体和该聚类中心之间距离的最大值；dmin表示聚类中心之间距离的最小值.若存在两组中心距离小于dmin，则将此两组合并为一组；若存在与所有组中心距离均大于dmax的个体，则以该个体形成一个新组.算法的具体实现步骤如下.

step1 将种群内的个体依照适应度降序排列；

step2 在[1，N]之间随机生成整数k，并将其作为初始小生境的数量；

step3 将排列后的前k个个体分别作为小生境中心放入不同的小生境中.检查是否所有小生境间距离均大于dmin，若不满足，则将小生境合并，并选择新的小生境中所有个体的中心；

step4 针对其它N-k个个体，计算其与已有小生境中心间距离.若距离比dmax大，则生成新小生境，并以该个体作为小生境中心.否则将该个体放入距离最近的小生境中.检查小生境中心之间距离是否都比dmin大，若不满足则合并对应的小生境；

step5 所有个体放置完成以后，将小生境中心固定，按照最小距离原则把所有个体安排到最近的小生境中；

step6 按式(4)完成种群中每个个体的共享值s(i)的计算；

step7 计算每个个体共享后的适应值；

step8 按照共享后的适应值完成遗传操作(包括选择、交叉和变异)，并形成下一代种群.

算法的发明人Yin和Germay将适应值共享算法与自适应k均值聚类算法结合使用，结果表明这样可以提高算法的运行效率.与前两种适应值共享算法相比较，本算法没有要求解空间中所有峰半径均相同.实践表明，结合适应值共享的k均值聚类算法能够提高标准适应值共享算法的运行效率.但缺点是算法在接近收敛时可能产生错误聚类.

3 几种适应值共享算法性能比较分析

适应值共享算法的执行在遗传算法的选择阶段之前.算法通过修改个体的适应度实现种群的多样性，以防止算法早熟并提高搜索的效率.标准适应值共享算法通常认为峰的分布是均匀的，并具有相同半径，但实际问题的求解中很难满足这个要求.但由于标准适应值共享算法运行效率稳定，所以该算法可以满足对峰的探索性需要.而结合适应值共享的k均值聚类算法能够减少标准适应值共享算法的时间，提高算法运行效率，但接近收敛时可能发生错误聚类.在实际应用中我们需要根据实际情况完成适应值共享小生境遗传算法的设计.

参考文献：

[1]华洁，崔杜武.基于个体优化的自适应小生境遗传算法[J].计算机工程，2010(1):194-196.

[2]周洪伟，徐松林，徐静.改进的小生境遗传算法[J].微计算机信息，2007(18):208-209.

[3]张俐.基于小生境遗传算法的MTSP问题求解[J].系统工程，2009(7):119-121.

[4]徐程，郑洪源.基于小生境遗传算法的关联规则挖掘研究[J].中国制造业信息化，2008(23):67-70.