基于视觉引导的Delta型并联机器人运动优化
2018-06-28,,
,,
(华中科技大学船舶与海洋工程学院,湖北 武汉 430074)
0 引言
Delta型并联机器人由2个正三角形平台和3组摆杆机构连接组成,3组主动臂链接在静平台上,从动臂将主动臂与动平台铰接。从动臂一般由碳纤维材料制成,具有轻便、强度大的特性,因此在工作时机构的动平台能获得较高的速度和加速度。如今Delta型并联机器人依靠其快速性及精确性的特点,被广泛应用于食品、药品包装和芯片加工等行业。
抓取过程中,Delta机器人通常采用门形路径,即2个竖直和1个水平方向的运动。由于门形路径会在竖直和水平方向过渡处引起较大冲击,通常采用加速度曲线修正的方法改善冲击。文献[1]中提出了一种改进型正弦修正梯形加速度曲线,得到了Delta端加速度最小的优化参数,消除了运动始末端的振动冲击,但方法仍基于门形路径和固定运动周期规划,未能提高抓取速度。文献[2]中提出采用三次多项式差值来规划轨迹,轨迹平滑,但轨迹仍停留在点对点运动,并未解决抓取速度及多目标优化问题。在实际工况中,当抓取速度一定时,通过优化多目标抓取轨迹优化减小抓取路径,可以提高整体抓取效率。另外,Delta机器人工作空间近似为半球形,当抓取位置接近工作空间边缘时,机构在此处的可控性和平稳性显著降低,此时极易发生动作畸变、机构肢解等状况。因此,还需对机械手的抓取工作空间进行优化,使其尽量处于机构运动中心附近,以保持机构良好的平稳性[3]。
在此,以Delta机器人的抓取工况为背景,以综合优化Delta机器人的抓取速度和机构平稳性为目的,提出一种基于视觉引导的优化算法。该算法基于实时视觉识别,在得到各工件的实时位置后,预测工件在抓取时到达的实际位置,结合Delta机器人工作空间规划抓取路径,同时针对视觉识别中的轨迹优化问题,通过粒子群算法,对抓取轨迹具有尽可能短的路径、机构具有尽可能优的平稳性进行综合评估,在确保工件之间不相互干扰的同时,提高抓取效率。
1 系统组成及原理
1.1 系统组成
基于视觉引导的Delta型并联机器人系统原理如图1所示。系统由以下几部分构成:CCD视觉相机,来料传动带、成品传送带及其驱动电机,Delta机器人与上位机。系统工作时,两传送带相向运行,工件随机摆放在来料传送带上,CCD视觉相机通过触发信号进行图像采集,在对图像进行识别和去重复化处理后,将工件的类别、坐标和角度等信息发送至上位机中,上位机通过对相机坐标与世界坐标的坐标变换并预测工件抓取时刻工件位置,反解出运动参数控制主动臂,完成工件抓取动作并将工件放于成品传送带的工件盒内。

图1 系统组成
1.2 工作空间的分析
Delta型并联机器人运动学正反解和工作空间计算问题,已有大量文献进行研究,本文不作赘述。


(1)

(2)
式中
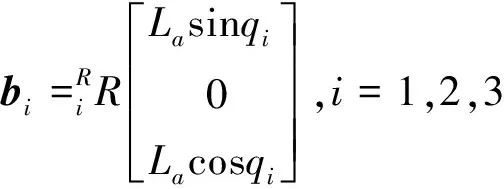
si为从动杆BiCi的方向向量。
将式(2)、bi和Delta机器人的结构参数(表1)代入速度及加速度雅可比矩阵中,可以求解出机构从工作空间中心到工作空间中各点的速度和加速度。从计算结果可知,机构的振动冲击在工作空间边缘位置较大,此时连续的启停将严重影响机构稳定性,因此,优化机构的抓取路径以减小机构在此处的冲击,能有效提升机构平稳性。

表1 Delta机器人结构参数
2 粒子群算法运动优化
2.1 轨迹设计
抓取工况时,Delta型并联机器人通常采用门形路径或平滑过度门轨迹,采取的运动策略为PTP点对点运动。为避免在抓取过程中工件之间的相互碰撞,会在轨迹中规划一段抓取高度H1,同时为了解决工件放置时叠放高度变化问题,在轨迹中规划一段可变的放置高度H2;为减小机械振动,在门形路径的转角处采取正弦曲线平滑过渡,Delta机器人平滑过渡门轨迹示意如图2所示[5-6]。
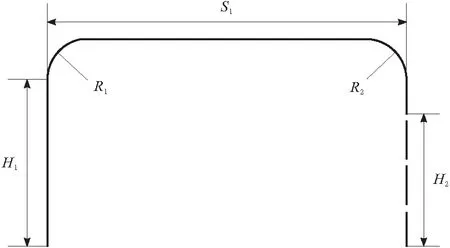
图2 平滑过度门轨迹示意
2.2 粒子群优化算法
Delta机器人分拣过程中,抓取路径长短和机构平稳性优劣是对机器人抓取效果影响最大的2个因素,本文选取二者作为优化目标函数。
a.抓取路径最短模型。
Delta机器人的效率可以表示为单位时间内抓取工件的数量,在抓取平均速度一定的情况下,单位时间内抓取工件的数量与抓取路径的长短有关。设Delta机器人拾取工件后放置位置为(x0,y0,0),第i个工件的位置为(xi,yi,0),v表示来料传送带的速度(沿x正方向),h表示抓取高度,ti表示Delta机器人从开始抓取到抓取到工件i之间的总抓取时间,其抓取路径最短可表示为:
(3)
式中
n为相机识别的工件数量;Sij为机器人从工件i到工件j抓取路径;Xij为决策变量,表示Delta机器人是否从工件i到工件j实施抓取。当Xij=1时,Delta机器人进行从工件i到工件j的抓取任务;当Xij=0时,Delta机器人不进行从工件i到工件j的抓取任务。
b.机构平稳性最优模型。
考虑到抓取时机构的振动冲击会对Delta机器人的抓取成功率及机构平稳性造成影响,过大的机械振动会导致机器人抓取中错抓、漏抓等情况,同时也会影响到Delta机器人的使用寿命,因此将机械臂末端的位移和加速度乘积大小作为衡量机构平稳性的因素。可以通过虚功原理,计算出Delta机器人抓取时机械臂杆件的虚功,用于评估系统的振动冲击。设Delta机器人从动杆长度为L,抓取过程中没有外部力作用,抓取时机构平稳性最优可表示为:
(4)

(5)
式中
δij1,δij2和aij1,aij2分别为机器人从工件i到工件j抓取时杆件两端的位移和加速度,可以通过机器人雅可比矩阵求解。
相关约束条件为:
xi,yi,xi+vti∈Q,i=1,2,3,…,n
(6)
aij1,aij2≤amax
(7)
vij1,vij2≤vmax
(8)
i≠j
(9)
(10)
约束条件(6)表示抓取的工件需在工作空间内,否则Xij=0,即机器人不实施抓取;约束条件(7)表示杆件两端加速度需小于机构最大加速度;约束条件(8)表示杆件两端速度需小于机构最大速度;约束条件(9)表示机器人不重复抓取工件;约束条件(10)表示机器人规划路径中抓取数量小于等于放置工件总数量n。
对于Delta机器人的抓取路径和机构平稳性建立目标函数[7-8]:
(11)
本文将抓取路径和机构平稳性视为权重w:1的优化目标,无量纲化后得出目标函数为:
minf(x)=
(12)
上述模型中,减小抓取路径会使加速距离减小,机构加速度增大,从而引起机构平稳性降低;反之,增加机构平稳性会使得加速段路径增大,路径无法最优。为使抓取路径和机构平稳性2个目标函数同时达到相对最优,本文引入多目标粒子群算法,算法求解过程如下。
a.算法初始化。初始化种群、迭代次数、粒子速度等,读取Delta机器人机构参数和目标工件位置参数等。
b.调用优化目标函数,计算抓取路径和机构平稳性最优模型,并更新种群粒子速度、位置和工件实时位置。
c.判断目标函数是否达到最优,若达到最优,则停止计算,输出计算结果;反之,则增加迭代次数进入步骤b重复运行。
算法流程如图3所示。
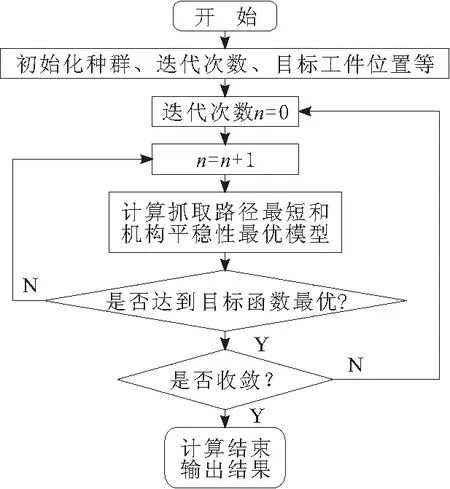
图3 优化算法流程
2.3 优化仿真模型
为验证算法可行性,在MATLAB的Simulink中建立优化仿真模型,如图4所示。

图4 优化仿真模型
3 仿真及实验验证
3.1 仿真验证
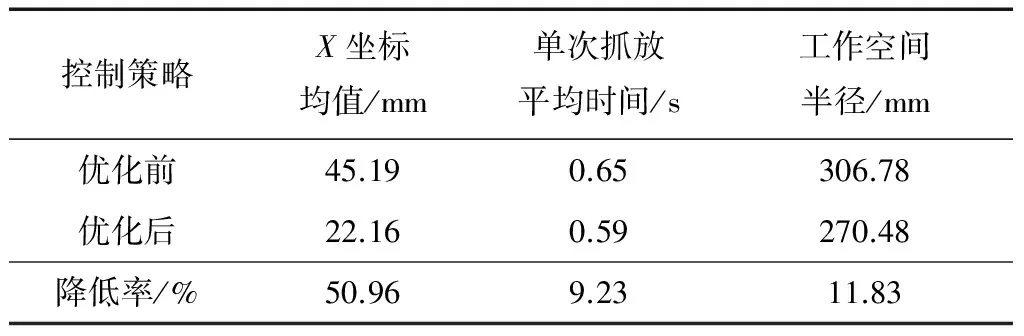
表2 100个/min工件密度正态分布下优化前后对比

表3 120个/min工件密度正态分布下优化前后对比

表4 100个/min工件密度平均分布下优化前后对比

表5 120个/min工件密度平均分布下优化前后对比
仿真结果表明,在工件密度相同的条件下,优化后的抓取工件横坐标、单次抓放平均时间和工作空间半径较优化前减小,平均分布下的优化效果较正态分布效果好;在分布情况相同的条件下,工件密度小的优化效果更为显著。
3.2 实验验证
为验证优化算法在实际工作时的抓取效果,进行了样机实验。实验用的Delta机器人分拣系统基于BECKHOFF CX5130系列嵌入式控制器进行开发,通过TwinCAT3进行PLC编程实现实时控制,该嵌入式系统主频为1.75 GHz,能满足实验的实时性要求。为保证每次实验时工件相对位置与仿真相同,将工件按相应的分布方式打印在图纸上以模拟实际工况,CCD工业相机拍摄帧率为100 Hz,传送带速度分别设定为100 mm/s,120 mm/s。系统的最大加速度为30 m/s2,最大速度为4.5 m/s,能满足抓取实验的硬件要求。搭建的实物系统如图5所示。

图5 实验样机
实验时,以抓取500个工件为1次实验,进行10次实验并求各项数据均值,得到实验结果如表6和表7所示。

表6 正态分布实验结果

表7 平均分布实验结果
为得到优化前后2种抓取方式的最大抓取速率,以比较二者工作效率,在确保不漏抓的情况下,改变传送带的速率,得到样机的实验结果如表8所示。
实验结果表明,在相同工况下,优化算法提高了抓取效率,降低了机械手末端振动冲击,提高了机构平稳性。对比单次抓取优化[3],本文算法更具普遍性,在提高生产效率的同时,有效降低了机器损耗。

表8 最大抓取速率
4 结束语
针对视觉引导的Delta型并联机器人,提出了一种基于全局目标抓取的运动优化算法。该算法通过计算抓取路径最短模型和机构平稳性最优模型得出决策变量实施抓取,利用MATLAB进行了数值仿真计算并采用实验样机证明了算法的可行性。该优化算法对于提高Delta型并联机器人的生产效率、减小生产工具的损耗,具有实际工程价值。
参考文献:
[1] 李云辉.Delta并联机器人抓放轨迹优化[J].电气自动化,2016,38(3):20-22,70.
[2] 王娜,王冬青,赵智勇.三自由度Delta并联机械手运动学分析及轨迹规划[J].青岛大学学报(工程技术版),2017,32(1):63-68.
[3] 毛洪国. 基于动力学模型的DELTA机器人运动控制研究[D].哈尔滨:哈尔滨工业大学,2014.
[4] 李旭宇,何风,尹东方.基于逆位移解的DELTA机器人工作空间分析[J].微电机,2017,50(8):75-79.
[5] 倪鹤鹏,刘亚男,张承瑞,等.基于机器视觉的Delta机器人分拣系统算法[J].机器人,2016,38(1):49-55.
[6] Ding W,Gu J,Tang S, et al. Development of a calibrating algorithm for Delta robot's visual positioning based on artificial neural network[J]. Optik - International Journal for Light and Electron Optics,2016,127(20):9095-9014.
[7] Zhang G Y,Liu G F,Guo X B,et al.Dynamic conveyor tracking control of a Delta robot[J].Key Engineering Materials,2016, 679:43-48.
[8] 卢锦玲,苗雨阳,张成相,等.基于改进多目标粒子群算法的含风电场电力系统优化调度[J].电力系统保护与控制,2013,41(17):25-31.
