多级圆柱齿轮减速器一体化结构系统显式动力学仿真研究

,,,

(1.沈阳飞机工业(集团)有限公司工程技术中心，辽宁 沈阳 110034;2.东北大学机械工程与自动化学院，辽宁 沈阳 110004)

0 引言

齿轮减速器是机械领域最重要的传动装置之一，广泛应用于航空、航天、冶金和交通等多个领域，对国民经济的发展具有重要意义[1-2]。

通过研究发现，目前大多数减速器的数值模拟研究，都简化了减速器系统中轴承或壳体的主要特征[3-5]，或者使用最弱的齿轮动力学作为减速器系统的性能指标，将整个减速机简化为单级齿轮轴传动系统[6]； 甚至减速机系统被简化为1对齿轮副进行分析[7-8]。然而，这些研究没有考虑齿轮轴相互的弯曲和扭转变形、轴承和齿轮的接触变形之间等耦合关系的影响; 特别是对于多级齿轮减速器系统，这种简化不能真实地模拟减速器系统实际工作的动态特征。

基于上述原因，以某三级直齿轮减速器传动一体化系统为研究对象，基于LS-DYNA对其整体结构进行显式动力学仿真分析。此方法能够综合考虑减速器整体传动系统的接触变形、轴系变形的相互影响关系，更加真实地反应减速器中各齿轮的弯曲应力和接触应力、各轴的弯扭变形及应力，以及各轴承的接触应力等动力学特性。

1 显式动力学模型

1.1 系统控制方程与显式积分[9]

三级减速器系统的多体冲击-碰撞的动力学模型为：

(1)

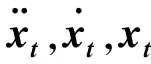
(2)

将式(2)代入动力学基本方程式(1)得：

(3)

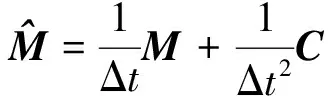
1.2 接触-碰撞的数值算法

物体A与B接触不嵌入的条件为：

VA∩VB=0

(4)

物体A与B不重叠条件为：

(5)

物体A与B接触面条件为：

(6)

U为坐标值；n为节点；t为接触力。从节点nS与主节点mS、主片Si关系分别如图1、图2所示，且满足条件式(7) ～式(10)。

(7)

S=g-(g·m)m

(8)

S=max(g·Ci/|Ci|)，i=1,2,…

(9)

(10)

C为边界；S为投影；g为任一矢量；m为边界系数；r为位置矢量。求解C坐标(ξc,ηc)。通过罚函数法计算主片Si各节点接触力。

图1 从节点与最近主节点的位置关系

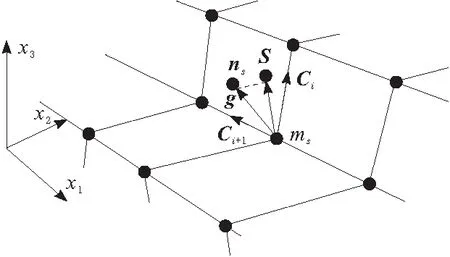
图2 从节点与主片的接触

2 显式接触动力学分析

2.1 模型的建立

在Pro/E三维建模软件中，建立包含3对直齿轮、8个滚动轴承和4根轴的减速器一体化实体模型如图3所示。

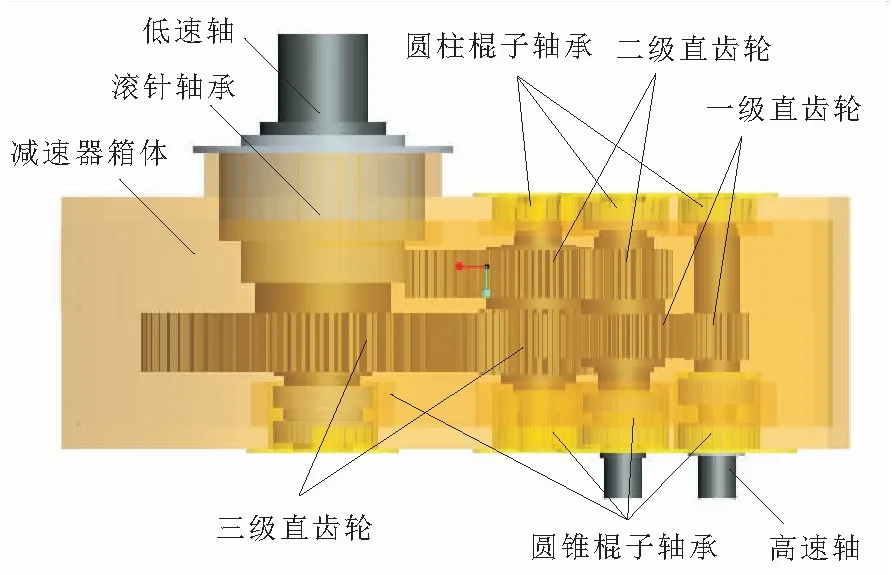
图3 三级减速器整体模型

2.2 接触界面定义[9]

通过动摩擦系数Fs，静摩擦系数Fd，指数衰减系数Dc，以及相对速度Vr决定接触摩擦系数，即

μc=Fd+(Fs-Fd)e-DcVr

(11)

用粘性摩擦系数Vc来限定最大摩擦力Fl，即

Fl=Vc·Ac

(12)

Ac为接触部分的接触面面积。Vc的表达式为：

(13)

σ0为接触材料的屈服应力。

为解决不真实振荡问题，通过设置阻尼系数来消除这种不切实际的振荡。阻尼系数定义为：

(14)

Vd为粘性阻尼系数。

ξcrit=2mω

(15)

2.3 接触刚度罚因子的选择

接触刚度为：

(16)

Fs为罚因子(默认为0.1)；A为接触面积；K为接触单元的体积模量；V为体积；M为实体单元。

2.4 网格划分

减速器系统的网格划分需要注意如下几个关键问题。

a.基于有限元方法的计算原理，相比于四面体网格，六面体网格可以获得更好的计算精度，并且在精度相同的情况下，网格数量的需求很少，因此，对于齿轮、轴承、轴和衬套网格划分，本研究采用solid164六面体。箱体采用solid164退化四面体形式划分。

b.相应网格数量增加，计算结果趋近于准确值，计算结果越接近于准确值，计算结果将趋于稳定并基本不受网格数量影响，但此时网格增加会降低计算速度。针对此种情况，首先定义一个网格大小进行计算，接着在此基础上采用0.5倍网格大小，再次进行仿真试算，当2次的计算结果基本无变化时确定网格数量规模。

c.在进行网格划分时，为确保网格的重要部分是密集的，不重要的位置是稀疏的。对于轴承滚子、轴承的内外圈、齿轮轴齿轮和轮齿，采用调节段数和网格大小进行控制，而对于齿轮、衬套和箱体，采用粗网格进行控制。此方式提高了准确性和效率。

通过上述关键问题的研究，最终三级齿轮减速器一体化系统的有限元网格模型如图4所示。

图4 减速器整体及各零部件的网格划分结果

2.5 PART的创建与接触对

在建立有限元模型后，一共有各零件所对应的PART号291个，参数设置包括材料(MAT)、类型(TYPE)、实常数(REAL)和当前被选择的单元(USED)，如表1所示。

表1 PART表

对齿轮减速器建立712对接触对，材料的摩擦系数参考机械设计手册，静摩擦系数为0.2，动摩擦系数为0.1。

2.6 加载

输入输出端轴外圈定义为刚体，主轴施加转速，被动轴施加力矩，转速为5 000 r/min，转矩为100 000 N·mm，加载APDL加载程序。

2.7 K文件的修改

由于三级减速机一体化整体模型复杂且极庞大，因此需要容量较大的内存，但计算机默认内存无法达到计算要求。采用方法为修改文件内存为200 000 000 kB，扩展内存要求。且IGNORE更改为1，以消除初始穿透的影响。

3 三级减速器结果分析与验证

3.1 结果分析

通过如前所述的三级齿轮减速器的建模进行显式仿真分析，获得各零部件应力云图，限于篇幅，只展示了第2轴系的零件和第3轴系特殊部件的应力云图，如图5所示。

图5 三级直齿轮减速器动态应力结果

提取齿轮减速器系统整体的最大等效应力-时间曲线，如图6所示。由图6可知，系统在刚启动时由于转速突然的施加造成系统的振动，随着时间的推移这种振动逐渐的减小，系统进入稳定运行阶段。可以看出这种振动与速度是非线性增加的关系。

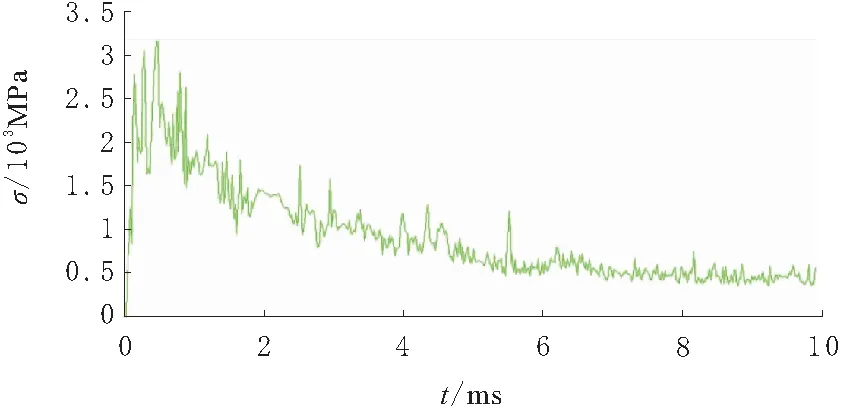
图6 减速器系统总体最大等效应力

同时，可以从分析结果中提取到系统整体以及各个部件的位移、速度、加速度、应力等动力学特性曲线。高速轴齿轮齿面上的某一点的应力曲线如图7所示。由图7可知，有2个峰值，一个为单齿啮合，另一个为双齿啮合；开始啮合时接触应力迅速上升为660 MPa，双齿啮合为355 MPa，与理论分析一致。

图7 齿面接触应力-时间历程曲线

齿根弯曲应力-时间历程曲线如图8所示。由图8可知，齿根弯曲应力的变化趋势与齿面接触应力基本相同，充分表明齿轮啮合时的交替单齿和双齿啮合过程。图8实线表示齿根弯曲压应力，虚线表示齿根弯曲拉应力。可以看出，齿根弯曲压应力(实线)大于齿根弯曲拉应力(虚线)，并且也与理论一致。

图8 齿根弯曲应力-时间历程曲线

3.2 结果验证

为验证仿真分析结果的正确性，对于高速运转齿轮轴的齿面接触应力，本研究采用赫兹理论进行计算，通过对比分析来验证结果的正确性。

基于赫兹理论的齿轮齿面接触应力为：

(17)

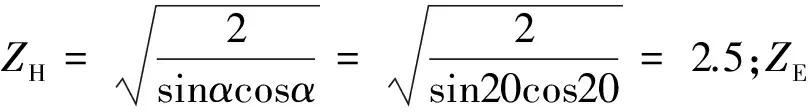
由ANSYS/LS-DYNA分析得到高速轴的齿面接触应力为280 MPa，理论计算值分别比实际分析值大8%，数据表明理论计算值比分析值偏大，符合赫兹理论保守的原则，验证了仿真分析结果的正确性。

4 结束语

对三级减速器一体化整体结构进行动力学仿真分析，没有过多简化结构特征，能够考虑减速器各级齿轮轴之间的弯扭变形/弯曲变形等耦合特性下的动力学性能。通过与赫兹理论解析算法的计算结果比较可知，仿真分析结果与理论解析结果基本吻合，符合理论分析，验证了显式动力学仿真分析结果的正确性。该方法能够准确预测减速器系统的动态特性，为齿轮减速器的优化设计提供重要的技术手段。

参考文献：

[1] Yang Q J. Fatigue test and reliability design of gears[J]. International Journal of Fatigue, 1996, 18(3): 171-177.

[2] Peng X Q, Liu G, Wu LY, et al. A stochastic finite element method for fatigue reliability analysis of gear teeth subjected to bending[J]. Computational Mechanics,1998,21(3):253-261.

[3] Zhang Y M, Liu Q L, Wen B C.Practical reliability-based design of gear pairs[J].Mechanism and Machine Theory,2003, 38(12):1363-1370.

[4] 杨劢.三级减速器动力学分析及系统可靠性评估[D].沈阳：东北大学,2013.

[5] 唐进元,刘艳平.直齿面齿轮加载啮合有限元仿真分析[J]. 机械工程学报,2012,48(5):124-131.

[6] 付胜, 吕孟宸.齿轮故障的仿真分析与研究[J].机械科学与技术,2016,35(9):1370-1374.

[7] 佟操,孙志礼,马小英,等.考虑安装与制造误差的齿轮动态接触仿真[J].东北大学学报 (自然科学版),2014,35(7): 996-1000.

[8] 孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京：科学出版社,2003.

[9] 李裕春,时党勇，赵远.ANSYS 10.0/LS-DYNA基础理论与工程实践[M].北京：中国水利水电出版社,2006.

第36卷 第6期2018年6月MACHINERY&ELECTRONICSVol．36No．6June2018