基于宏程序的非圆二次曲线数控车削编程与加工研究

张 武

(云南开放大学 机电工程学院，云南 昆明 650500)

数控车削加工是一种在车床上利用工件的旋转及刀具的相对运动实现对回转体表面零件进行切削加工的一种加工方法，主要包括内外圆柱面、圆锥面、螺纹及圆弧表面等零件的加工。近年来，随着装备制造的不断发展以及工业产品性能要求的不断提高，在一些高精度的航空航天零部件生产中，各种复杂的非圆二次曲线零件(如双曲线、椭圆及抛物线)的加工也日渐增多[1]，在这类复杂零件中，非圆二次曲线的加工质量好坏往往成为整个零件生产制造的关键。

非圆二次曲线是一种利用二元二次方程来表达轮廓形状的复杂曲线，其轮廓零件在数控车削中属于较复杂的零件类别。由于目前行业内常用的数控系统自身没有二次曲线插补(编程)功能，不能对如双曲线、椭圆及抛物线等非圆二次曲线零件进行直接编程加工，致使目前行业内对复杂二次曲线零件的车削加工一直是个比较棘手的问题。在目前实际的加工生产中，对非圆二次曲线传统的加工方法主要是采用计算机辅助制造CAM软件进行编程加工，该编程方法虽然能实现加工目的，但因受到软件所编写的程序段较长、可读性差和程序修改不方便等缺点的影响，以及受到数控机床通信接口、程序传输和场地及加工人员素质等条件限制，一般情况下，特别是在有时间限制的数控技能大赛中，利用率并不是很高[2]。

针对上述问题，通过对非圆二次曲线轮廓的近似数学模型及数控机床插补原理进行分析研究，并结合多年的数控加工生产经验，提出了利用数控系统插补原理，把非圆二次曲线“无限分割，以直代曲”，用微小直线段把加工对象上的每个点连接起来，近似地表达(拟合)曲线轮廓，并采用宏指令的方法编写出凹椭圆面的加工程序，实现了非圆二次曲线的车削加工。

1 数控机床插补原理分析

在数控加工过程中，为了满足加工对象几何尺寸精度的要求，数控机床刀具中心轨迹必须准确地依照工件的轮廓形状来生成。对于简单的直线或圆弧，数控机床易于实现；然而，对于复杂形状的二次曲线，若直接生成刀具中心轨迹，势必会使算法变得非常复杂，数控系统的计算工作量也会大大增加。因此，在实际应用中，常常利用工程数学微积分原理，采用一小段直线去近似地逼近(拟合)被加工的曲线轮廓(见图1)。加工时，向数控系统输入加工曲线上的已知坐标点(通常为曲线起点、终点)，数控系统随即根据曲线段的方程及特征，应用一定的算法，在刀具运动过程中实时计算出满足曲线线形和进给速度要求的若干中间点，自动地在有限坐标点之间生成一系列的坐标数据，即对其进行数据密化，这就是数控加工中的插补原理[3]。这样，曲线的实际轮廓就是由一段段的折线拼接而成，虽然是折线，但是因为每一段走刀线段(步长)都设得非常小(在精度允许范围内)，所以由N段折线拟合组成的插补曲线是可以近似地逼近实际曲线轮廓的。

图1 用微小直线段来拟合曲线

2 宏指令编程原理分析

宏指令是数控系统的一种特殊功能，利用宏指令编写的加工程序其实是一种带有变量的子程序，它具有赋值、计算、循环、跳转及选择等功能[4]。在编程时，可像计算机高级语言一样，使用变量对曲线轨迹进行算术运算、逻辑运算和函数混合运算[5]。程序执行时，可利用数控系统提供的变量功能、数学运算功能、逻辑判断功能、条件转移及程序循环等功能，来计算出加工中刀具运动的实时坐标值，从而实现一些特殊曲线加工。

通过利用宏指令编写的加工程序，具有程序简捷、高效、逻辑严密，可读性和通用性强、便于检查及修改等特点。目前，数控系统中的宏程序可分为A类和B类，其中B类宏程序在生产实际中用得比较广泛，且使用简单方便，本文采用B类宏程序来对实例中凹椭圆面的加工进行分析研究。

3 非圆二次曲线编程与加工实例

非圆二次曲线主要包括双曲线、椭圆及抛物线，其中最具代表性的是椭圆曲线。由于三者的数学方程均为二元二次方程，且特征相似，所以本文以椭圆曲线轴的加工为例，对非圆二次曲线的宏指令编程及加工进行分析。

3.1 椭圆轮廓线的近似数学模型分析

椭圆曲线轴零件图如图2所示。在数控车削加工过程中，假想把加工对象凹椭圆曲线无限分割，以直代曲，用微小直线段把加工对象上的每个点连接起来，近似地表达(拟合)椭圆曲线。在实际的车削过程中，数控车床的加工平面为XZ平面，加工坐标轴为X轴和Z轴，因此在编写宏程序时，一般把Z作为自变量，X作为因变量[6]。这样数控系统在每执行1个Z方向加工步长时即产生1个与之对应的X值。编程时，可以把经过数学处理的椭圆方程中的X以变量的方式编写入宏程序，利用数控系统的变量、计算、循环及跳转等功能自动计算出所需的实时的X值，加工时，刀具再按照计算出的X值和Z值来连续运动实现切削加工。

椭圆标准方程为：

(1)

根据数控车床加工轴X和Z，把式1转换为对应坐标轴方程：

(2)

式中，Z代表数控车床Z坐标轴；X代表数控车床X坐标轴。再根据椭圆已知条件：长半轴为25 mm，短半轴为22 mm，变换式2得到：

(3)

若以Z为自变量时，加工到达某一点的X实时坐标值，变换式2后得：

(4)

带入椭圆长、短半轴值得：

式中，a、b分别为对应的椭圆长半轴和短半轴。编程时，把a、b和Z值分别进行变量赋值，并把X以因变量的方式带入宏程序，即可编写出数控系统能够执行的加工宏程序。

图2 椭圆曲线轴零件图

根据图2及椭圆轮廓线的近似数学模型分析，对宏程序变量定义如下：

#101—椭圆Z方向加工起点；变量值#101=18.87；

#102—椭圆长半轴a，变量值#102=25；

#103—椭圆短半轴b，变量值#103=-22；

#104—椭圆加工中到达某一点的X实时坐标值(直径值)；即#104=#103*SQRT[1-[#101*#101]/[ #102*#102]]；

3.2 凹椭圆面加工工艺分析

图2所示零件的曲线部分主要由2个焦点在X轴上且长半轴为25 mm，短半轴为22 mm，椭圆中心偏移零件中心41.5 mm的凹椭圆面及3个R6.5的圆弧组成。零件加工时，采用三爪自定心卡盘一夹一顶装夹完成零件中间曲线部分的加工，两端外圆台阶的编程及加工由于方法较简单，这里就不再叙述。编程时，主要以零件中间2个椭圆和3个R6.5的圆弧精加工为例，来详细分析宏程序的编写方法。在加工椭圆1时，需用G55指令把工件坐标系原点设置在距零件右端面Z向-55 mm的零件中心；而在加工椭圆2时，则需调用G56指令把工件坐标系原点设置在距零件右端面Z向-101 mm的零件中心。

加工时，材料选用φ60 mm×160 mm的45钢，刀具选用35°菱形车刀。加工参数为：粗加工时留0.5 mm的精加工余量(该部分省略)，精车转速2 000 r/min，进刀深度0.5 mm，进给量0.15 mm/r，Z轴切削步距0.05 mm。

3.3 编写零件精加工程序(三菱数控系统)

该零件曲线部分的加工编程采用宏指令编程方式实现，其加工宏程序控制流程图如图3所示。编写椭圆和R6.5圆弧部分的精加工宏程序如下：

O0010；主程序

G54 G0 X250 Z200 T0101；(调用G54工件坐标系，坐标原点为工件右端面圆心)

S2000 M03；

M08;

G0 X62 Z-27；(精加工起点)

X58;

G01 Z-31.51 F0.15;

G03 X54.14 Z-36.13 R6.5;(开始加工第1个圆弧R6.5)

G55 M98 H150;(调用G55工件坐标系，把坐标系原点设置在距离工件右端面Z方向-55 mm的零件中心(见图2)，并调用150号子程序开始椭圆1的插补)

G01 X53.38 Z-18.49 F0.15;

G03 X53.38 W-9.03 R6.5;(开始插补第2个圆弧R6.5)

G56 M98 H150;(调用G56工件坐标系，把坐标系原点设置在距工件右端面Z方向-101 mm的工件中心，并调用150号子程序开始椭圆2的插补)

G03 X58 W-4.62 R6.5; (开始插补第3个圆弧R6.5)

G01 W-4;(Z方向加工外圆4 mm)

G0 X62;

X250 Z2 M05;(退刀，机床主轴停止)

M09；

M30; (程序结束)

N0150;(子程序)

#101=18.87; (定义Z轴方向椭圆加工起点)

#102=25; (定义椭圆长半轴)

#103=-22; (定义椭圆短半轴及加工方向)

N70 #104=#103*SQRT[1-[#101*#101]/[ #102*#102]]; (计算X因变量的坐标值)

G01X[2*#104+83] Z[#101] F0.15; (开始进行椭圆插补，83为凹椭圆中心偏移零件中心的直径值)

#101=#101-0.05; (计算插补时Z轴坐标值，加工步距为0.05 mm)

IF [#101 GE-18.87] GOTO 70; (条件判断,当Z轴未到-18.87 mm时跳转至N70继续执行)

M99; (子程序结束并返回主程序)

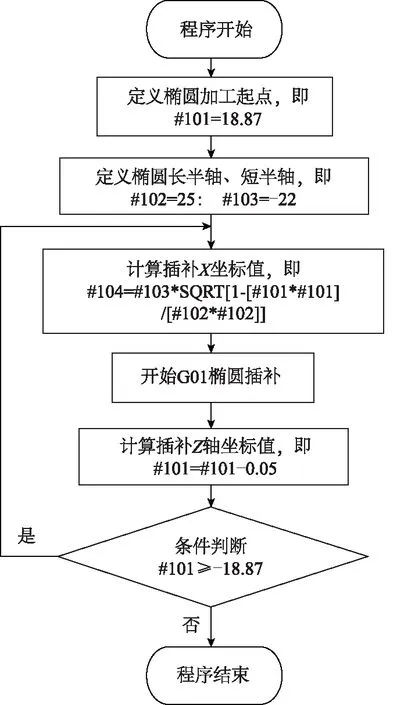
图3 椭圆加工宏程序控制流程图

经过实际加工验证，加工出的凹椭圆曲线轴精度完全达到图样要求，加工的零件实物图如图4所示。

图4 零件实物图

4 结语

针对非圆二次曲线在数控车削中加工困难的问题，根据数控机床直线(圆弧)插补原理，把椭圆曲线无限分割，以直代曲，近似地逼近(拟合)椭圆曲线，编写出了零件加工宏程序(编程模板)，经过实际加工验证，加工出的凹椭圆曲线轴精度完全达到图样要求。在实际应用中，只需把加工程序中的椭圆方程改为其他非圆曲线方程，并进行相应变化，即可实现其他非圆曲线的编程加工。该编程方法不仅拓宽了现有数控车床的车削范围，使得过去一直难以加工的复杂二次曲线的加工变得简单化，利用同样的原理还可以推广至双曲线、抛物线、余弦曲线及正弦曲线等轮廓的生产加工。

[1] 王丽珍. 浅谈非圆曲线在数控车床加工程序中的应用[J]. 中国新技术新产品，2012(1): 154.

[2] 金方军. 非圆二次曲线轮廓的数控车宏程序编程与加工[J]. 机电工程技术，2009,38(5): 47-48,63,1.

[3] 曹智梅. 数控车床曲线方程的宏程序编制[J]. 机床与液压,2012(14): 141-143.

[4] 钮忻旸. 椭圆形零件轮廓线的数学模型及加工方法[J]. 石油矿场机械,2004,33 (5): 113-115.

[5] 赵宏立. 非圆二次曲线数控宏程序的编制与应用[J]. 机械，2010(8): 62-65.

[6] 肖忠跃，刘朝辉，谢世坤. 基于Fanuc 0i系统的椭圆类轮廓零件宏程序应用研究[J]. 煤矿机械，2013,34(1): 145-146.