正交异性薄膜非线性振动分析

何泽青, 张冬辉, 宋 林, 栗颖思, 王 生

(1． 中国科学院大学 材料科学与光电技术学院， 北京 100190； 2． 中国科学院 光电研究院， 北京 100094)

随着浮空器研究的迅速发展和新兴建筑领域的兴起，现代复合膜材料由于其高强、轻质、柔软、化学稳定等特性得到了广泛的应用[1]。膜结构由于质量轻、张力大，普遍存在大变形、低频率的振动特点，当薄膜结构的固有频率与外界激励频率非常接近时，结构极容易发生共振甚至导致破坏，因此膜结构的动力学问题引起了人们的广泛关注，对于膜结构自振特性的研究也就显得尤为必要。

当前对于膜结构振动研究主要分为线性领域和非线性领域。在线性领域，文献[2]对于各向同性张拉薄膜的自由振动进行了理论分析，并对具有规则外形的矩形和圆形薄膜的振动频率和振型进行了理论求解；文献[3]根据哈密顿原理建立了薄膜法向振动的动力学方程，求得周边固定圆形薄膜、扇形薄膜自由振动的理论解；文献[4]求解了各向同性的双向受力不等的矩形、圆形、椭圆形平面薄膜的自振频率与振型，并给出了任意外形边界的平面薄膜的近似解，但分析中并未考虑薄膜正交异性情况，同时动力学方程中也未体现出非线性对结构振动的影响；文献[5]构造了6节点三角形单元，根据哈密顿原理建立薄膜自由振动方程，并推导其单元刚度矩阵和单元质量矩阵。文献[6]用Bessel函数作为薄膜横向振动偏微分方程的解，建立复杂边界固有频率求解模型，并对圆形、L-形、分段圆弧边界平面张 不拉薄膜固有频率进行求解，分析了边界几何参数对薄膜固有频率的影响。文献[7]建立了薄膜二维振动的偏微分方程，并对无限大薄膜的二维受迫振动一般方程进行了求解。以上模态分析均是建立在初始几何形态上，没有考虑结构法向位移对其几何形态的影响，这在小变形假定下是可以接受的。但是，膜结构本身由于具有较强的几何非线性特点，其大变形效应对曲面本身有一定的修正作用，同时其形态的不稳定必然会对其刚度矩阵产生较大的影响。

在非线性领域，目前主要有能量法、范式理论方法、同伦摄动法和迭代摄动法等对非线性振动展开近似求解。文献[8]基于能量原理求出非线性系统的一次近似解析解，然后利用牛顿迭代思想得到周期系数微分方程，最后根据谐波平衡原理及最小二乘法求其高次近似解。文献[9]拓展了范式方法，改进了Nayfeh关于响应频率的提取，使其可以研究强非线性振动问题。文献[10]利用微分求积法计算了变密度薄膜的横向振动，获得了系统无量纲复频率与密度系数、薄膜张力比的关系曲线。文献[11]应用了一种推广的平均法研究强非线性振子的共振响应，并与数值积分法进行了对比。文献[12]通过两个典型张拉膜结构工程实例采用Lanczos法研究了膜面初张力、膜面矢高和膜材质量对自振特性的影响，分析结果表明膜面张力与结构质量是影响膜结构自振特性的主要因素，大变形产生的位移修正效应对膜结构自振特性也有较大的影响。文献仅是通过仿真分析对上述现象进行阐述，并未从理论上对其进行分析和说明。

本文将参考Qian的研究对于各向同性的双向受力不等平面薄膜的振动分析，对正交异性薄膜振动进行数理分析，建立薄膜振动的平衡微分方程，同时更进一步的根据薄膜振动的大挠度理论[13-14]引入其动力学方程的非线性项，考虑薄膜的正交异性和振动中的非线性特点，对动力学方程进行求解，得出非线性振动频率的解析解，目的是明确非线性因素对于振动频率的影响。同时为了提高理论研究在工程应用中的便利性，通过对方程解析解进行合理简化，得到一种简单精确，适用于工程需要的非线性频率计算公式。

1 动力学方程

1.1 动力学微分方程

建立如图1所示的坐标系，在振动的膜上选取一振动的微单元，l1和l2为微元表面的弧线，l1与XOZ平面平行，l2与YOZ平面平行。

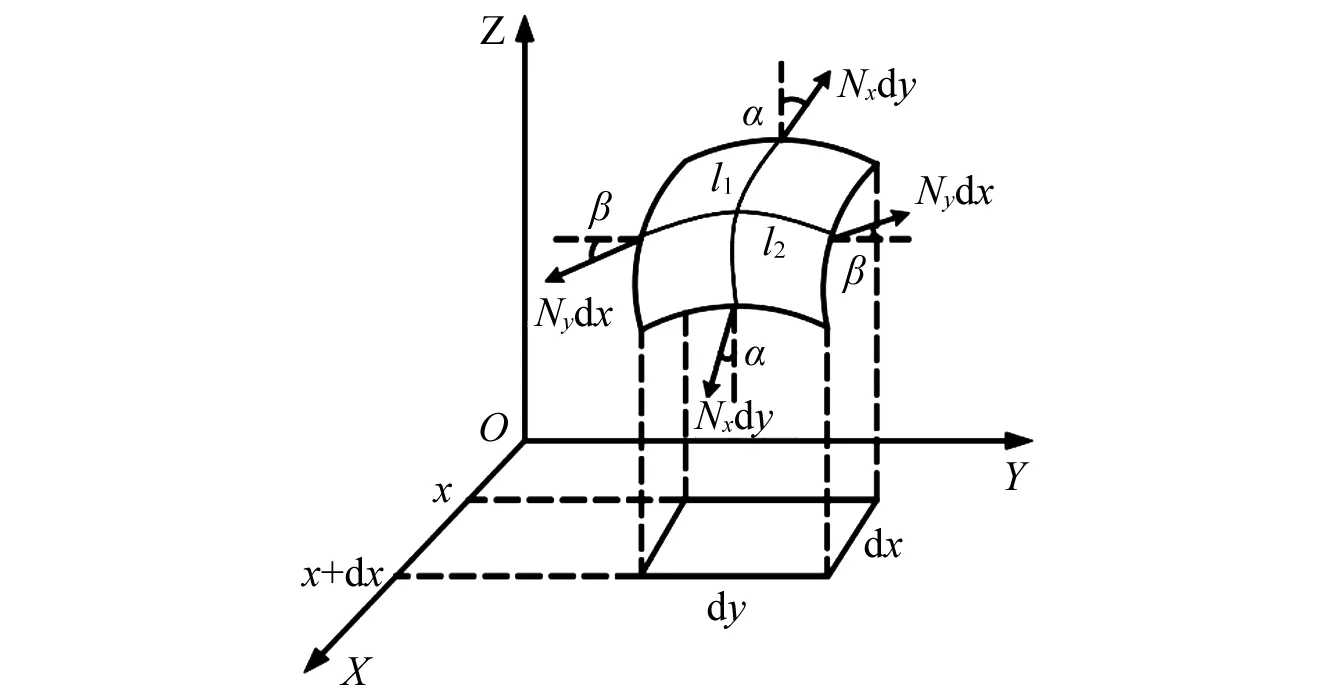
图1 振动的膜微元Fig.1 Vibrating micro-membrane unit

在微元dy边界，单位长度的张力为Nx，沿微元切线方向，与X坐标轴夹角为α，因此作用在x端的单位长度的张力在Z轴方向的分量为Nxsinα，由于α较小，则有sinα≈tanα，用w表示膜面上一点在振动中的挠度，因此有

于是作用在整个dy边上的Z轴方向的力为

而在x+dx端的Z轴方向的力应为

由此可得在该面元的x与x+dx边上Z轴方向的合力为

同理，作用在dx边界上的的张力在Z轴方向的合力可以表示为

所以作用在整个微元上Z轴方向的合力为

设膜的面密度为ρ，则微元的质量为ρdxdy，根据达朗贝尔原理可写出微元的运动微分方程

整理后可得

(1)

式中：Nx为微元dy边界单位长度的张力，沿微元切线方向；Ny为微元dx边界单位长度的张力，沿微元切线方向；w为微元挠度；ρ为微元的面密度。

对于受预张力薄膜在法向载荷下的振动微分方程，在式(1)中加入预张力和法向载荷项，就可以得到在法向载荷作用下，正交异性双向受力不等的预张力薄膜振动微分方程

(2)

式中：Nox为微元dy边界单位长度的预张力，沿微元切线方向；Noy为微元dx边界单位长度的预张力，沿微元切线方向；p(x,y,t)为微元法向载荷。

1.2 变形协调方程

根据弹性大挠度理论[15]，薄膜变形后，其应变由线性和非线性两部分组成。其中，线性应变由面内位移u,v引起，非线性应变由挠度w引起，因此总的应变为

(3)

式中：εx为微元沿l1方向的应变；εy为微元沿l2方向的应变；γxy为切应变；u为微元沿l1方向的面内位移；v为微元沿l2方向的面内位移。

将式(3)中的位移u，v消去后可得膜面应变与挠度必须满足的变形连续条件，即相容方程

(4)

1.3 物理方程

根据膜材料的均匀性与正交异性假定，纤维方向为弹性主方向，令其与l1，l2方向一致。按正交异性理论，l1和l2两个方向的弹性模量分别为E1和E2，剪切模量为G12，径向泊松比为μ1，纬向泊松比为μ2，弹性模量与泊松比满足下面的关系式

(5)

根据应力应变物理方程关系式有

(6)

即有

(7)

式中：σx为微元dy边界的正应力，沿微元切线方向；σy为微元dx边界的正应力，沿微元切线方向；τxy为微元切应力；h为膜材厚度。

将式(7)代入相容方程式(4)中，得到{N}用w表示的相容方程

(8)

1.4 控制方程组的建立

总结以上内容，可得正交异性薄膜非线性振动问题的控制方程组为

(9)

式中：Nox为微元dy边界单位长度的预张力，沿微元切线方向；Noy为微元dx边界单位长度的预张力，沿微元切线方向；Nx为微元dy边界单位长度的张力，沿微元切线方向；Ny为微元dx边界单位长度的张力，沿微元切线方向；Nxy为微元的面内剪切力；ρ为微元的面密度；h为微元厚度；E1为微元沿l1方向的弹性模量；E2为微元沿l2方向的弹性模量；G12为剪切模量；μ1为微元沿l1方向的泊松比；μ2为微元沿l2方向的泊松比；w=w(x,y,t)为微元挠度；p(x,y,t)为微元法向载荷。

在薄膜振动过程中，根据膜面无矩无剪力假定[16]，同时引入应力函数φ(x,y,t)[17]

(10)

对于自由振动薄膜，取其法向力p(x,y,t)=0，将式(10)代入式(9)，则控制方程组为

(11)

2 方程简化

2.1 初始条件与边界条件

以四周固支的矩形薄膜为例，如图2所示。

图2 四周固支的矩形薄膜Fig.2 Rectangular membrane with four edges clamped

在矩形薄膜边界处，其挠度在振动过程中始终为零，并且运动的速度也为零，即薄膜应满足如下边界条件：

x=0或a时

(12)

y=0或b时

(13)

t=0时

(14)

以上三组边界和初始条件即为薄膜在振动过程中的定解条件，在确定薄膜的模态参数时将会用到。

2.2 控制方程组简化

根据函数的性质，对w(x,y,t)采用分离变量法进行求解，设满足边界条件的位移函数为[18]

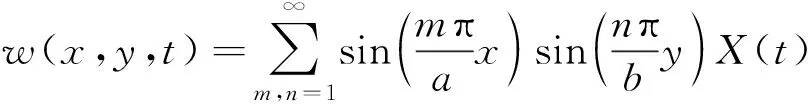
式中：w(x,y,t)为膜面挠度；m为x方向的节线数，取正整数；n为y方向的节线数，取正整数；a,b为矩形膜面的边长；X(t)为膜面挠度最大值的时间函数。

将上式只取一项进行求解，再将最终结果按上式进行求和计算，并不影响最终结果，则可以得到

(15)

将式(15)代入式(11)的第二式可以得到

(16)

(17)

将式(17)代入式(16)可得

将式(17)代入边界条件式(12)和式(13)可得

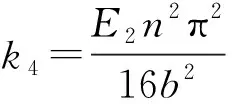
将上面所得的系数ki代入式(17)可得

(18)

将式(18)代入式(10)的前两式可得

(19)

(20)

将式(15)、式(19)、式(20)代入式(11)的第一式可得

(21)

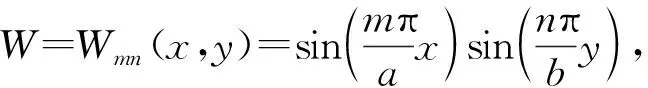
(22)

3 方程求解

根据式(22)的推导得到薄膜振动频率方程的非线性表达式，对于式(22)可以采用利兹-伽辽金法进行求解[19]，取权函数为W,构造积分方程为

(23)

其中，

式(23)为一个典型的非线性振动Duffing方程[20]，由于X3(t)的系数B并非为一个微小量，因此式(23)为一个强非线性振动方程。

3.1 方程的解析解

根据方程(23)可得

(24)

由式(15)可知，当t=0时有

令X(0)=A，表示初始时刻(t=0)膜面挠度的最大值，有

根据边界条件式(14)，当t=0时

将上式再次代入式(24)，有

(25)

对上式进行变量分离，得

薄膜从平衡位置到最大位移A处需要经历1/4周期，因此对上式展开积分

则可以得到薄膜振动的周期T为

(26)

将上式代入式(26)并进行积分可得

将p和q代入上式，则可以得出薄膜振动的频率f为

(27)

式(27)即为正交异性薄膜非线性振动频率的解析解的表达式。由上式可见，薄膜振动频率的非线性解不仅包含其频率的线性部分，同时还与薄膜经纬方向的弹性模量有关，并且受薄膜振动初始位移的影响。

3.2 方程的近似解

根据边界条件式(14),可以设式(23)的解为

X(t)=Acos(ωt)=Acosφ=X

取权函数为cosφ，代入式(23)，并经由伽辽金法在一个周期T内积分得

(28)

将X=Acosφ代入式(28)，可得

(29)

由式(29)可得

得出

即

(30)

式(30)即为正交异性薄膜非线性振动频率的近似解的表达式。

3.2 非线性项对频率的影响分析

对于薄膜振动微分方程式(23)，若令其非线性项系数B=0，则可以得到标准的线性振动微分方程

(31)

对式(31)进行求解则可以得到薄膜振动频率的线性频率f0的表达式为

(32)

由式(30)和式(32)可得

(33)

令

从式(23)可知，B,K>0，因此ε>0，则式(33)可转化为

(34)

从式(34)可以看出，薄膜的非线性自由振动仍然为周期振动，但振动的频率值随薄膜初始位移A的变化而变化，而不同于线性系统的固有频率，如图3所示。

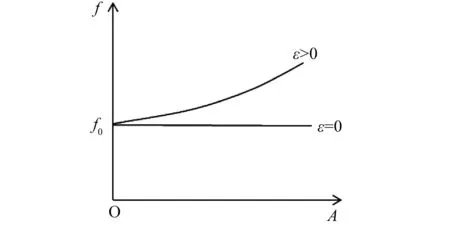
图3 非线性自振频率-初始位移曲线Fig.3 Nonlinear frequency according to different initial displacement

4 算例分析

以图2所示的四周固支矩形薄膜为例，分别对其自振频率的线性解、非线性解析解和非线性近似解进行计算，并展开比较分析。薄膜参数为：a=2 m，为薄膜长边长度；b=1 m，为薄膜短边长度；ρ=0.12 kg/m2，为薄膜面密度；Nox=5 000 N/m，为膜面x向预张力；Noy=2 500 N/m，为膜面y向预张力；h=0.16 mm，为薄膜厚度；E1=0.8 GPa，为薄膜x向弹性模量；E2=0.6 GPa，为薄膜y向弹性模量。

4.1 自振频率的线性解

将K代入式(32)，则可以得到薄膜自振频率的线性解公式

(35)

从式(35)中可以看出，由于并未考虑正交方向不同的弹性模量的影响以及挠度引起的薄膜面内应力的变化所带来的影响，而是按均匀各向同性材料来考虑，因此其线性频率值仅与初始条件以及边界条件有关。下面将对其前八阶线性频率进行计算，如表1所示。

表1 自振频率的线性解

4.2 自振频率的非线性理论解

根据式(27)计算振动频率的解析解。首先以一阶(m=1,n=1)频率为例，确定其收敛性。

编制程序，取初始位移A=0.02 m，计算f11与j的关系如表2所示。

表2 解析解的收敛性

从表2可以看出，当j≥2时，计算结果即收敛于稳定值，可以判定频率的解析解是快速收敛并趋于稳定的。

根据式(27)，取j=100，则正交异性薄膜非线性振动前八阶频率的解析解，如表3所示。

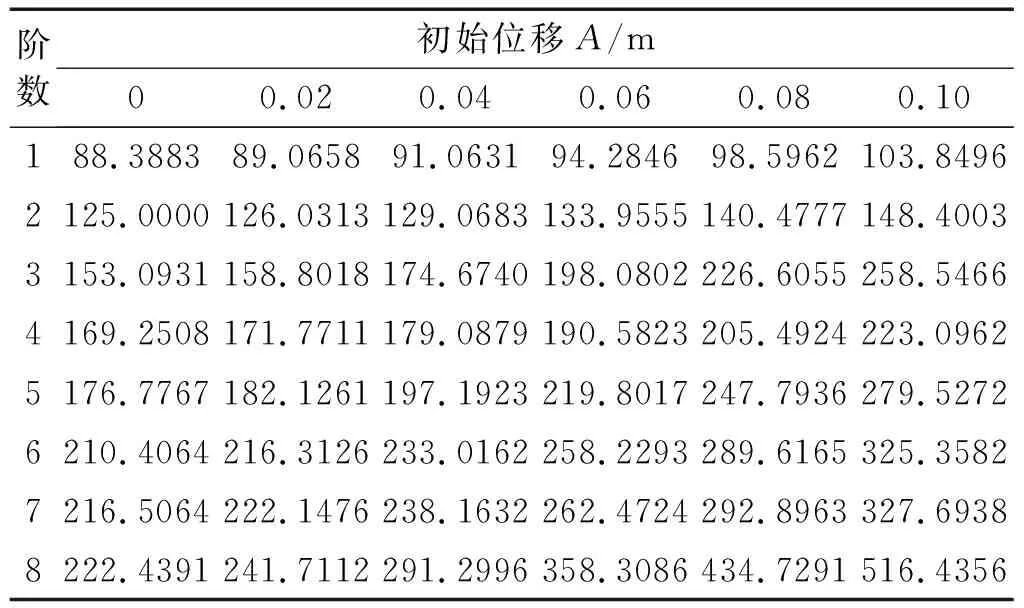
表3 自振频率的非线性解析解

自振频率的解析解随初始位移变化情况如图4所示。

从表3可以看出，当初始位移为0时，薄膜的自振频率与其按小挠度计算得到的线性解相同；而从图4可以看出，随着初始位移的增加，薄膜的自振频率也逐渐变大，这是由于随着初始位移的增加，薄膜面内应力增大，导致薄膜刚度增大，从而引起其振动频率变大。

图4 前八阶频率-初始位移曲线Fig.4 The first eight modal frequencies according to different initial displacement

4.3 自振频率的非线性近似解

式(30)为经由伽辽金算法得出的正交异性薄膜非线性振动频率的近似解，其频率公式为

其前八阶计算频率如表4所示。

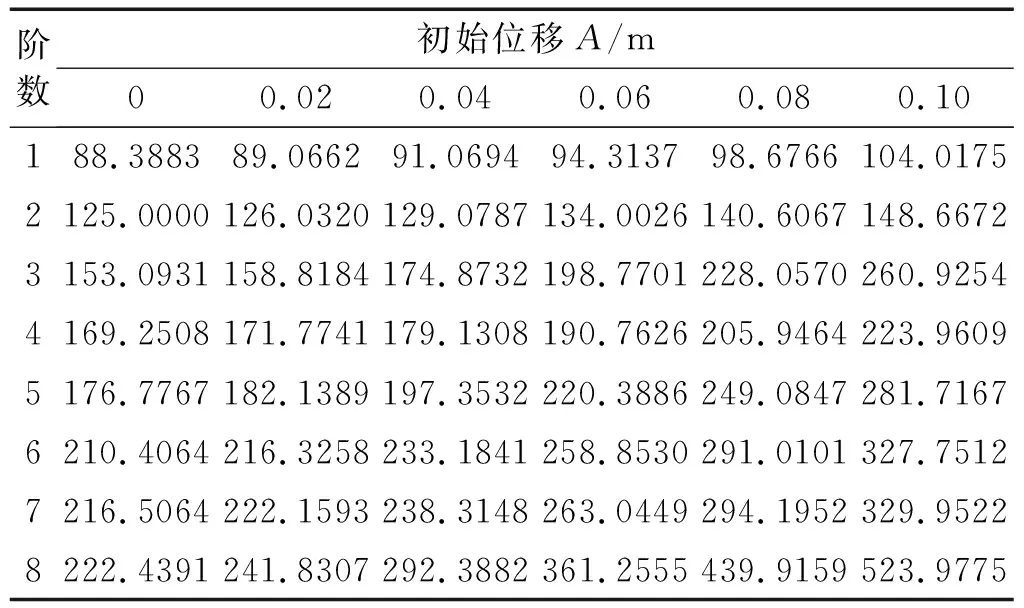
表4 自振频率的非线性近似解

薄膜自由振动前三阶理论解与近似解的对比如图5～图7所示。

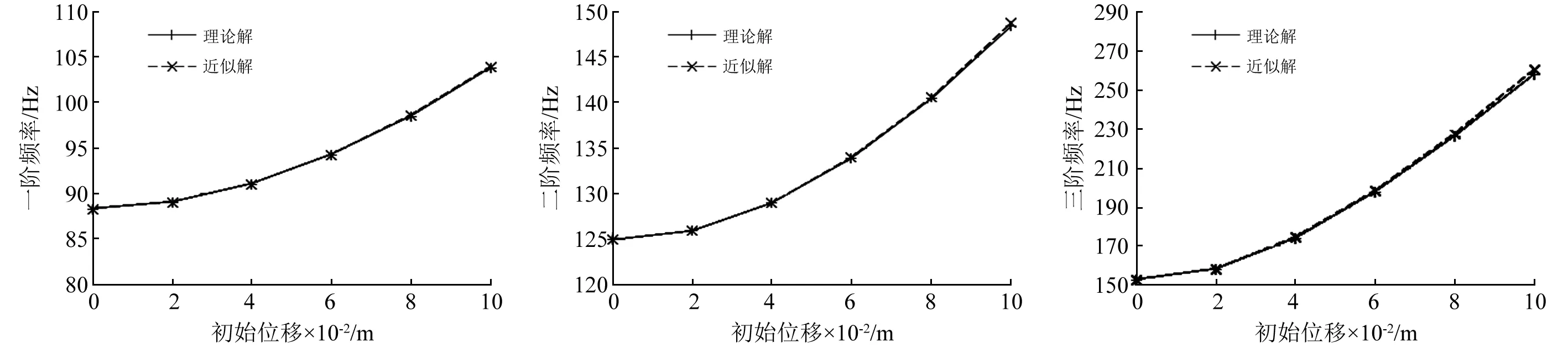
图5 一阶频率-初始位移曲线Fig.5 The first order frequency according to different initial displacement图6 二阶频率-位移曲线Fig.6 The second order frequency according to different initial displacement图7 三阶频率-位移曲线Fig.7 The third order frequency according to different initial displacement

图5～图7显示了薄膜一～三阶频率的理论解与近似解随初始位移的变化情况。从图中可以看出，近似解与理论解吻合情况良好，二者的误差随着初始位移的增加而逐渐增大，表4中的最大误差仅为1.46%。更进一步的，当A→∞时，频率的近似解与理论解的比值为即对于任意的初始位移，近似解与理论解的最大误差不超过3.86%。

5 结 论

本文通过建立正交异性薄膜的非线性振动微分方程并对其进行求解，得到了其振动频率的理论解，同时利用伽辽金法对方程进行了简化求解，并得到了其近似解。利用此两种解分别对四边简支矩形正交异性薄膜结构的线性频率和非线性自由振动频率分别进行了求解计算和对比，结果表明：

(1)薄膜结构线性振动分析仅适用于小挠度情况。

(2)随着薄膜初位移的增加，导致薄膜面内刚度变大，进而引起其频率变大。

(3)本文得到的薄膜自振频率的近似解简单实用，且具有较高的精度，对于任意的初始位移，按近似解表达式计算的结果与理论解的最大误差不超过3.86%，完全能够满足工程精度的要求。

综上所述，文中通过解析方法对正交异性薄膜的非线性振动展开分析，建立了结构的振动微分方程，方程在推导过程中并未对薄膜的结构形态进行特殊设定，因此其表达式是通用的，对于复杂形态的薄膜结构同样适用，当系统的结构形式和边界条件明确时，可以通过解析方法得出非线性系统的理论解或近似解。相较于数值方法，解析法由于不存在截断误差和舍入误差，因此具有更高的精度，同时避免了数值方法在迭代计算过程中可能出现的不易收敛问题。为了提高分析结果的工程适用性，文中利用伽辽金法对非线性振动的Duffing方程进行求解并对结果展开误差分析，得到的近似解不仅适用于线性和弱非线性系统，对强非线性系统同样适用，因此具有较大的适用范围和较高的精度，丰富和完善了非线性振动的研究，其研究结果为浮空器和建筑膜结构的工程设计提供了理论计算依据。

参 考 文 献

[ 1 ] 陈务军. 膜结构工程设计[M]. 北京: 中国建筑工业出版社, 2004: 134-139.

[ 2 ] TIMOSHENKO S, YOUNG S H, WEAVER W. Vibration problems in engineering[M]. 4th ed. New York: John Wiley & Sons, 1974: 327-334.

[ 3 ] 林文静, 陈树辉, 李森. 圆形薄膜自由振动的理论解[J]. 振动与冲击, 2009, 28(5): 84-86.

LIN Wenjing, CHEN Shuhui, LI Sen. Analytical solution of the free vibration of circular membrane[J].Journal of Vibration and Shock, 2009, 28(5): 84-86.

[ 4 ] QIAN Guozhen. Solution for free vibration problem of membrane with unequal tension in two directions[J]. Applied Mathematics and Mechanics, 1982, 3(6): 885-892.

[ 5 ] 林文静, 陈树辉. 平面薄膜自由振动的有限元分析[J]. 动力学与控制学报, 2010, 8(3): 202-206.

LIN Wenjing, CHEN Shuhui. Free vibration analysis of plane membranes by finite element method[J]. Journal of Dynamics and Control, 2010, 8(3): 202-206.

[ 6 ] 刘充, 李玉宇, 保宏, 等. 边界几何参数对空间平面张拉膜结构固有频率影响研究[J]. 振动与冲击, 2015, 34(20): 198-202.

LIU Chong, LI Yuyu, BAO Hong, et al. Natural frequencies of pre-tensioned membrane structure with different boundary geometrical parameters [J]. Journal of Vibration and Shock, 2015, 34(20): 198-202.

[ 7 ] 张俊生. 薄膜二维振动数理方程的推导与求解[J]. 榆林学院学报, 2006, 16(6): 29-31.

ZHANG Junsheng. Inferential reasoning solution of thin film 2D vibration M&P equation [J]. Journal of Yulin University, 2006, 16(6): 29-31.

[ 8 ] 周一峰. 强非线性系统周期解的能量法[J]. 力学季刊, 2002, 23(4): 514-520.

ZHOU Yifeng. Energy iteration method for analytic periodic solutions of full strongly nonlinear vibration systems[J]. Chinese Quarterly Mechanics, 2002, 23(4): 514-520.

[ 9 ] 张琪昌, 郝淑英, 陈予恕. 用范式理论研究强非线性振动问题[J]．振动工程学报, 2000, 13(3): 481-486．

ZHANG Qichang, HAO Shuying, CHEN Yushu. Study on strongly non-linear vibration systems by normal form theory [J]. Journal of Vibration Engineering, 2000,13(3): 481-486.

[10] 武吉梅, 陈媛, 王砚， 等. 基于微分求积法的印刷运动薄膜动力稳定性分析[J]. 振动与冲击, 2015, 34(20): 57-60.

WU Jimei, CHEN Yuan, WANG Yan, et al. Dynamic stability of printing moving membrane based on differential quadrature method [J]. Journal of Vibration and Shock, 2015, 34(20): 57-60.

[11] 徐兆, 詹杰民． 强非线性振子的受迫振动[J]． 中山大学学报(自然科学版), 1995, 34(2): 1-6．

XU Zhao, ZHAN Jiemin. Forced oscillations of strongly nonlinear oscillators [J]. Journal of Sun Yat-sen University(Natural Science), 1995, 34(2): 1-6．

[12] 余志祥, 赵雷. 张拉膜结构自振特性研究[J]. 西南交通大学学报, 2004, 39(6): 734-739.

YU Zhixiang, ZHAO Lei. Research on free vibration properties of membrane structure [J]. Journal of Southwest Jiaotong University, 2004, 39(6): 734-739.

[13] CHEN Shanlin, ZHENG Zhoulian. Large deformation of circular membrane under the concentrated force [J]. Applied Mathematics and Mechanics, 2003, 24(1): 28-31.

[14] WANG Jing. Nonlinear free vibration of the circular plate with large deflection [J]. Journal of South China University of Technology, 2001, 29(8): 4-6.

[15] LIU Changjiang, ZHENG Zhoulian, YANG Xiaoyan, et al. Nonlinear damped vibration of pre-stressed orthotropic membranestructure under impact loading [J]. International Journal of Structural Stability and Dynamics, 2014, 14(1): 1091-1115.

[16] 乔磊, 谭峰, 杨庆山. 薄膜结构的动力反应分析[J]. 振动与冲击, 2011, 30(6): 109-113.

QIAO Lei, TAN Feng, YANG Qingshan. Dynamic analysis of membrane structures [J]. Journal of Vibration and Shock, 2011, 30(6): 109-113.

[17] 徐芝纶. 弹性力学[M]. 4版. 北京: 高等教育出版社, 2006: 32-36.

[18] ZHENG Zhoulian, LIU Changjiang, HE Xiaoting, et al. Free vibration analysis of rectangular orthotropic membranes in large deflection [J]. Mathematical Problems in Engineering, 2009(4): 634362.

[19] 周纪卿, 朱因远. 非线性振动[M]. 西安： 西安交通大学出版社, 2001: 140-144.

[20] 刘延柱, 陈立群． 非线性振动[M]． 北京: 高等教育出版社, 2001: 59-60．